сист одноврем уравн примеры.ppt
- Количество слайдов: 61
 Системы одновременных уравнений
Системы одновременных уравнений
 Системы одновременных уравнений Пример 1. Требуется: 1. Оценить следующую структурную модель на идентификацию: y 1 = b 13 y 3 + a 11 x 1 + a 13 x 3 y 2 = b 21 y 1 + b 23 y 3 + a 22 x 2 y 3 = b 32 y 2 + a 31 x 1 + a 33 x 3 2. Исходя из приведенной формы модели уравнений y 1 = 2 x 1 + 4 x 2 + 10 x 3 y 2 = 3 x 1 - 6 x 2 + 2 x 3 y 3 = - 5 x 1 + 8 x 2 + 5 x 3 найти структурные коэффициенты модели.
Системы одновременных уравнений Пример 1. Требуется: 1. Оценить следующую структурную модель на идентификацию: y 1 = b 13 y 3 + a 11 x 1 + a 13 x 3 y 2 = b 21 y 1 + b 23 y 3 + a 22 x 2 y 3 = b 32 y 2 + a 31 x 1 + a 33 x 3 2. Исходя из приведенной формы модели уравнений y 1 = 2 x 1 + 4 x 2 + 10 x 3 y 2 = 3 x 1 - 6 x 2 + 2 x 3 y 3 = - 5 x 1 + 8 x 2 + 5 x 3 найти структурные коэффициенты модели.
 Системы одновременных уравнений Решение. 1. Модель имеет три эндогенные (y 1, y 2, y 3) и три экзогенные переменные (x 1 , x 2 , x 3). Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации. Первое уравнение. Н: эндогенных переменных – 2 (y 1, y 3), отсутствующих экзогенных – 1 (x 2). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в первом уравнении отсутствуют y 2 и x 2. Построим матрицу из коэффициентов при них в других уравнениях системы:
Системы одновременных уравнений Решение. 1. Модель имеет три эндогенные (y 1, y 2, y 3) и три экзогенные переменные (x 1 , x 2 , x 3). Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации. Первое уравнение. Н: эндогенных переменных – 2 (y 1, y 3), отсутствующих экзогенных – 1 (x 2). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в первом уравнении отсутствуют y 2 и x 2. Построим матрицу из коэффициентов при них в других уравнениях системы:
 Системы одновременных уравнений Уравнение Отсутствующие переменные y 2 x 2 Второе -1 a 22 Третье b 32 0 Det A = -1*0 -b 32* a 22 ≠ 0 Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.
Системы одновременных уравнений Уравнение Отсутствующие переменные y 2 x 2 Второе -1 a 22 Третье b 32 0 Det A = -1*0 -b 32* a 22 ≠ 0 Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.
 Системы одновременных уравнений Второе уравнение. Н: эндогенных переменных – 3 (y 1, y 2, y 3), отсутствующих экзогенных – 2 (x 1, x 3). Выполняется необходимое равенство: 3=2+1, следовательно, уравнение точно идентифицируемо. Д: во втором уравнении отсутствуют x 1 и x 3. Построим матрицу из коэффициентов при них в других уравнениях системы: Уравнение Отсутствующие переменные x 1 x 3 Первое a 11 a 13 Третье a 31 a 33
Системы одновременных уравнений Второе уравнение. Н: эндогенных переменных – 3 (y 1, y 2, y 3), отсутствующих экзогенных – 2 (x 1, x 3). Выполняется необходимое равенство: 3=2+1, следовательно, уравнение точно идентифицируемо. Д: во втором уравнении отсутствуют x 1 и x 3. Построим матрицу из коэффициентов при них в других уравнениях системы: Уравнение Отсутствующие переменные x 1 x 3 Первое a 11 a 13 Третье a 31 a 33
 Системы одновременных уравнений Det A = a 11 * a 33 - a 31 * a 13 ≠ 0 Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо.
Системы одновременных уравнений Det A = a 11 * a 33 - a 31 * a 13 ≠ 0 Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо.
 Системы одновременных уравнений Третье уравнение. Н: эндогенных переменных – 2 (y 2, y 3), отсутствующих экзогенных – 1 (x 2). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в третьем уравнении отсутствуют y 1 и x 2. Построим матрицу из коэффициентов при них в других уравнениях системы: Уравнение Отсутствующие переменные y 1 x 2 Первое -1 0 Второе b 21 a 22
Системы одновременных уравнений Третье уравнение. Н: эндогенных переменных – 2 (y 2, y 3), отсутствующих экзогенных – 1 (x 2). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в третьем уравнении отсутствуют y 1 и x 2. Построим матрицу из коэффициентов при них в других уравнениях системы: Уравнение Отсутствующие переменные y 1 x 2 Первое -1 0 Второе b 21 a 22
 Системы одновременных уравнений Det A = - 1 * a 22 - b 21* 0 ≠ 0 Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо. Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов. 2. Вычислим структурные коэффициенты модели: 1) Из третьего уравнения приведенной формы выразим x 2 (так как его нет в первом уравнении структурной формы): у3 + 5 х1 - 5 х3 x 2 = 8
Системы одновременных уравнений Det A = - 1 * a 22 - b 21* 0 ≠ 0 Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо. Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов. 2. Вычислим структурные коэффициенты модели: 1) Из третьего уравнения приведенной формы выразим x 2 (так как его нет в первом уравнении структурной формы): у3 + 5 х1 - 5 х3 x 2 = 8
 Системы одновременных уравнений Данное выражение содержит переменные у3 , х1 и х3, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение x 2 в первое уравнение приведенной формы модели (ПФМ): у1 = 2 x 1 + 4 у3 + 5 х1 - 5 х3 8 + 10 x 3 у1 = 0, 5 у3 + 4, 5 x 1 + 7, 5 х3 - первое уравнение СФМ; 2) Во втором уравнении СФМ нет переменных x 1 и х3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа:
Системы одновременных уравнений Данное выражение содержит переменные у3 , х1 и х3, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение x 2 в первое уравнение приведенной формы модели (ПФМ): у1 = 2 x 1 + 4 у3 + 5 х1 - 5 х3 8 + 10 x 3 у1 = 0, 5 у3 + 4, 5 x 1 + 7, 5 х3 - первое уравнение СФМ; 2) Во втором уравнении СФМ нет переменных x 1 и х3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа:
 Системы одновременных уравнений Первый этап: выразим x 1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения: x 1 = у1 - 4 х2 - 10 х3 2 = 0, 5 у1 – 2 х2 - 5 х3 Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует х3, которого нет в СФМ. Выразим из третьего уравнения ПФМ: x 3 = у3 + 5 х1 - 8 х2 5
Системы одновременных уравнений Первый этап: выразим x 1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения: x 1 = у1 - 4 х2 - 10 х3 2 = 0, 5 у1 – 2 х2 - 5 х3 Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует х3, которого нет в СФМ. Выразим из третьего уравнения ПФМ: x 3 = у3 + 5 х1 - 8 х2 5
 Системы одновременных уравнений Подставим его в выражение x 1 : у 3 + 5 х1 - 8 х2 x 1 = 0, 5 у1 – 2 х2 – 5 = 0, 5 у1 – у3 + 6 х2 - 5 x 1 = 0, 5 у1 - у3 + 6 х2 6
Системы одновременных уравнений Подставим его в выражение x 1 : у 3 + 5 х1 - 8 х2 x 1 = 0, 5 у1 – 2 х2 – 5 = 0, 5 у1 – у3 + 6 х2 - 5 x 1 = 0, 5 у1 - у3 + 6 х2 6
 Системы одновременных уравнений Второй этап: аналогично, чтобы выразить х3 через искомые у1, у3 и х2, заменим в выражении х3 значение х1 на полученное из первого уравнения ПФМ: x 3 = у3 + 5 (0, 5 у1 - 2 х2 - 5 х3) - 8 х2 = 5 = 0, 2 у3 +0, 5 у1 – 3, 6 х2 - 5 х3 Следовательно, x 3 = 0, 033 у3 + 0, 083 у1 – 0, 6 х2
Системы одновременных уравнений Второй этап: аналогично, чтобы выразить х3 через искомые у1, у3 и х2, заменим в выражении х3 значение х1 на полученное из первого уравнения ПФМ: x 3 = у3 + 5 (0, 5 у1 - 2 х2 - 5 х3) - 8 х2 = 5 = 0, 2 у3 +0, 5 у1 – 3, 6 х2 - 5 х3 Следовательно, x 3 = 0, 033 у3 + 0, 083 у1 – 0, 6 х2
 Системы одновременных уравнений Подставим полученные х1 и х3 во второе уравнение ПФМ: 0, 5 у1 - у3 + 6 х2 у2 = 3 - 6 х2 + 2 (0, 033 у3 + 0, 083 у1 – 0, 6 х2) 6 у2 = 0, 416 у1– 0, 434 у3 – 4, 2 х2 – второе уравнение СФМ Это уравнение можно получить из ПФМ и другими путями.
Системы одновременных уравнений Подставим полученные х1 и х3 во второе уравнение ПФМ: 0, 5 у1 - у3 + 6 х2 у2 = 3 - 6 х2 + 2 (0, 033 у3 + 0, 083 у1 – 0, 6 х2) 6 у2 = 0, 416 у1– 0, 434 у3 – 4, 2 х2 – второе уравнение СФМ Это уравнение можно получить из ПФМ и другими путями.
 Системы одновременных уравнений 3. Из второго уравнения ПФМ выразим х2 , так как его нет в третьем уравнении СФМ: - у2 + 3 х1 + 2 х3 х2 = = - 0, 167 у2 + 0, 5 х1 + 0, 0333 х3 6 Подставим полученное выражение в третье уравнение ПФМ: у3 = - 5 х1 + 8 (- 0, 167 у2 + 0, 5 х1 + 0, 0333 х3) + 5 х3 у3 = - 1, 336 у2 - х1 + 7, 664 х3 - третье уравнение СФМ.
Системы одновременных уравнений 3. Из второго уравнения ПФМ выразим х2 , так как его нет в третьем уравнении СФМ: - у2 + 3 х1 + 2 х3 х2 = = - 0, 167 у2 + 0, 5 х1 + 0, 0333 х3 6 Подставим полученное выражение в третье уравнение ПФМ: у3 = - 5 х1 + 8 (- 0, 167 у2 + 0, 5 х1 + 0, 0333 х3) + 5 х3 у3 = - 1, 336 у2 - х1 + 7, 664 х3 - третье уравнение СФМ.
 Системы одновременных уравнений Таким образом, СФМ примет вид: у1 = 0, 5 у3 + 4, 5 x 1 + 7, 5 х3 у2 = 0, 416 у1– 0, 434 у3 – 4, 2 х2 у3 = - 1, 336 у2 - х1 + 7, 664 х3
Системы одновременных уравнений Таким образом, СФМ примет вид: у1 = 0, 5 у3 + 4, 5 x 1 + 7, 5 х3 у2 = 0, 416 у1– 0, 434 у3 – 4, 2 х2 у3 = - 1, 336 у2 - х1 + 7, 664 х3
 Системы одновременных уравнений Пример 2. Изучается модель вида y = a 1 + b 1 (С + D) + ε 1 C = a 2 + b 2 y + b 3 y -1 + ε 2 y - валовой национальный доход; y-1 - валовой национальный доход предшествующего года; С - личное потребление; D - конечный спрос (помимо личного потребления); ε 1 и ε 2 – случайные составляющие.
Системы одновременных уравнений Пример 2. Изучается модель вида y = a 1 + b 1 (С + D) + ε 1 C = a 2 + b 2 y + b 3 y -1 + ε 2 y - валовой национальный доход; y-1 - валовой национальный доход предшествующего года; С - личное потребление; D - конечный спрос (помимо личного потребления); ε 1 и ε 2 – случайные составляющие.
 Системы одновременных уравнений Информация за девять лет о приростах всех показателей дана в табл. : год D y -1 y С 1 - 6, 8 46, 7 3, 1 7, 4 2 22, 4 3, 1 22, 8 30, 4 3 - 17, 3 22, 8 7, 8 1, 3 4 12, 0 7, 8 21, 4 8, 7 5 5, 9 21, 4 17, 8 25, 8 6 44, 7 17, 8 37, 2 8, 6 7 23, 1 37, 2 35, 7 30, 0 8 51, 2 35, 7 46, 6 31, 4 9 32, 3 46, 6 56, 0 39, 1 Σ 167, 5 239, 1 248, 4 182, 7
Системы одновременных уравнений Информация за девять лет о приростах всех показателей дана в табл. : год D y -1 y С 1 - 6, 8 46, 7 3, 1 7, 4 2 22, 4 3, 1 22, 8 30, 4 3 - 17, 3 22, 8 7, 8 1, 3 4 12, 0 7, 8 21, 4 8, 7 5 5, 9 21, 4 17, 8 25, 8 6 44, 7 17, 8 37, 2 8, 6 7 23, 1 37, 2 35, 7 30, 0 8 51, 2 35, 7 46, 6 31, 4 9 32, 3 46, 6 56, 0 39, 1 Σ 167, 5 239, 1 248, 4 182, 7
 Системы одновременных уравнений Для данной модели была получена система приведенных уравнений: y = 8, 219 + 0, 6688 D + 0, 2610 y-1 C = 8, 636 + 0, 3384 D + 0, 2020 y-1 Требуется: 1. Провести идентификацию модели. 2. Рассчитать параметры первого уравнения структурной модели. Решение.
Системы одновременных уравнений Для данной модели была получена система приведенных уравнений: y = 8, 219 + 0, 6688 D + 0, 2610 y-1 C = 8, 636 + 0, 3384 D + 0, 2020 y-1 Требуется: 1. Провести идентификацию модели. 2. Рассчитать параметры первого уравнения структурной модели. Решение.
 Системы одновременных уравнений Решение. 1. В данной модели две эндогенные переменные (у и С) и две предопределенные переменные (D и у Второе уравнение точно -1). идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1+1.
Системы одновременных уравнений Решение. 1. В данной модели две эндогенные переменные (у и С) и две предопределенные переменные (D и у Второе уравнение точно -1). идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1+1.
 Системы одновременных уравнений Первое уравнение сверхидентифицировано, так как в нем на параметры при С и D наложено ограничение: они должны быть равны. В этом уравнении содержится одна эндогенная переменная у. Переменная С в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с переменной D.
Системы одновременных уравнений Первое уравнение сверхидентифицировано, так как в нем на параметры при С и D наложено ограничение: они должны быть равны. В этом уравнении содержится одна эндогенная переменная у. Переменная С в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с переменной D.
 Системы одновременных уравнений В данном уравнении отсутствует одна экзогенная переменная, имеющаяся в системе. По счетному правилу идентификации получаем: 1+1=2: D +1>Н. Это больше, чем число эндогенных переменных в данном уравнении, следовательно, система сверхидентифицирована.
Системы одновременных уравнений В данном уравнении отсутствует одна экзогенная переменная, имеющаяся в системе. По счетному правилу идентификации получаем: 1+1=2: D +1>Н. Это больше, чем число эндогенных переменных в данном уравнении, следовательно, система сверхидентифицирована.
 Системы одновременных уравнений 2. Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов. Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной С.
Системы одновременных уравнений 2. Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов. Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной С.
 Системы одновременных уравнений Для этого в приведенное уравнение C = 8, 636 + 0, 3384 D + 0, 2020 y-1 подставим значения D и y-1, имеющиеся в условии задачи. Полученные данные занесем в таблицу.
Системы одновременных уравнений Для этого в приведенное уравнение C = 8, 636 + 0, 3384 D + 0, 2020 y-1 подставим значения D и y-1, имеющиеся в условии задачи. Полученные данные занесем в таблицу.
 Системы одновременных уравнений Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения С на теоретические Ĉ и рассчитываем новую переменную Ĉ+ D (см. табл. )
Системы одновременных уравнений Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения С на теоретические Ĉ и рассчитываем новую переменную Ĉ+ D (см. табл. )
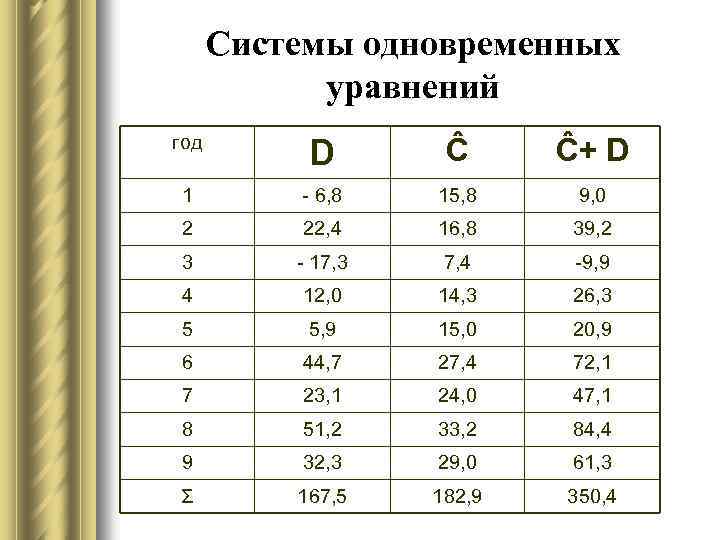 Системы одновременных уравнений год D Ĉ Ĉ+ D 1 - 6, 8 15, 8 9, 0 2 22, 4 16, 8 39, 2 3 - 17, 3 7, 4 -9, 9 4 12, 0 14, 3 26, 3 5 5, 9 15, 0 20, 9 6 44, 7 27, 4 72, 1 7 23, 1 24, 0 47, 1 8 51, 2 33, 2 84, 4 9 32, 3 29, 0 61, 3 Σ 167, 5 182, 9 350, 4
Системы одновременных уравнений год D Ĉ Ĉ+ D 1 - 6, 8 15, 8 9, 0 2 22, 4 16, 8 39, 2 3 - 17, 3 7, 4 -9, 9 4 12, 0 14, 3 26, 3 5 5, 9 15, 0 20, 9 6 44, 7 27, 4 72, 1 7 23, 1 24, 0 47, 1 8 51, 2 33, 2 84, 4 9 32, 3 29, 0 61, 3 Σ 167, 5 182, 9 350, 4
 Системы одновременных уравнений Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную Ĉ+ D через Z. Решаем уравнение у = a 1 + b 1 Z Система нормальных уравнений составит: Σу = na 1 + b 1 Σ Z Σу. Z = a 1 Σ Z + b 1 Σ Z 2 248, 4 = 9 a 1 + 350, 4 b 1 13508, 71 = 350, 4 a 1 + 21142, 02 b 1
Системы одновременных уравнений Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную Ĉ+ D через Z. Решаем уравнение у = a 1 + b 1 Z Система нормальных уравнений составит: Σу = na 1 + b 1 Σ Z Σу. Z = a 1 Σ Z + b 1 Σ Z 2 248, 4 = 9 a 1 + 350, 4 b 1 13508, 71 = 350, 4 a 1 + 21142, 02 b 1
 Системы одновременных уравнений Итак, первое уравнение структурной модели представляется в следующем виде: y = 7, 678 + 0, 512 (С + D)
Системы одновременных уравнений Итак, первое уравнение структурной модели представляется в следующем виде: y = 7, 678 + 0, 512 (С + D)
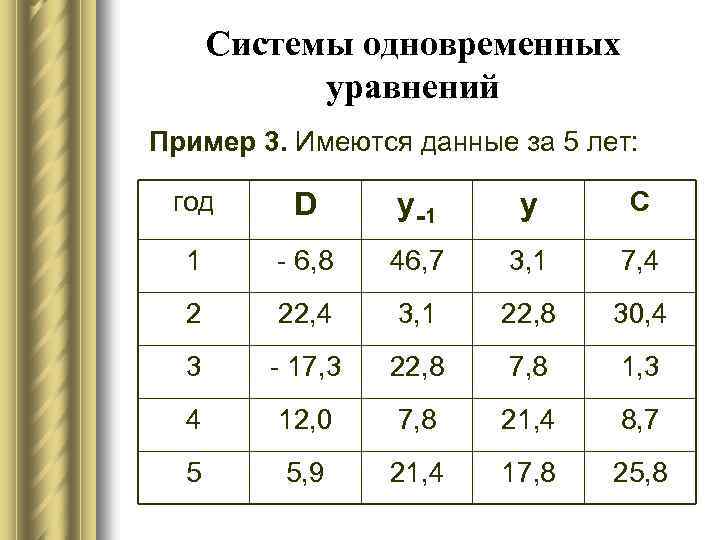 Системы одновременных уравнений Пример 3. Имеются данные за 5 лет: год D y -1 y С 1 - 6, 8 46, 7 3, 1 7, 4 2 22, 4 3, 1 22, 8 30, 4 3 - 17, 3 22, 8 7, 8 1, 3 4 12, 0 7, 8 21, 4 8, 7 5 5, 9 21, 4 17, 8 25, 8
Системы одновременных уравнений Пример 3. Имеются данные за 5 лет: год D y -1 y С 1 - 6, 8 46, 7 3, 1 7, 4 2 22, 4 3, 1 22, 8 30, 4 3 - 17, 3 22, 8 7, 8 1, 3 4 12, 0 7, 8 21, 4 8, 7 5 5, 9 21, 4 17, 8 25, 8
 Системы одновременных уравнений Требуется: Построить модель вида : y 1 = f (y 2, х1), y 2 = f (y 1, х2), рассчитав соответствующие структурные коэффициенты. Решение.
Системы одновременных уравнений Требуется: Построить модель вида : y 1 = f (y 2, х1), y 2 = f (y 1, х2), рассчитав соответствующие структурные коэффициенты. Решение.
 Системы одновременных уравнений Решение. Система одновременных уравнений с двумя эндогенными и двумя экзогенными переменными имеет вид: y 1 = b 12 y 2 + a 11 х1 + ε 1 y 2 = b 21 y 1 + a 22 х2 + ε 2
Системы одновременных уравнений Решение. Система одновременных уравнений с двумя эндогенными и двумя экзогенными переменными имеет вид: y 1 = b 12 y 2 + a 11 х1 + ε 1 y 2 = b 21 y 1 + a 22 х2 + ε 2
 Системы одновременных уравнений В каждом уравнении две эндогенные и одна отсутствующая экзогенная переменная из имеющихся в системе. Для каждого уравнения данной системы действует счетное правило 2=1+1. Это означает, что каждое уравнение и система в целом идентифицированы. Для определения параметров такой системы применяется косвенный метод наименьших квадратов.
Системы одновременных уравнений В каждом уравнении две эндогенные и одна отсутствующая экзогенная переменная из имеющихся в системе. Для каждого уравнения данной системы действует счетное правило 2=1+1. Это означает, что каждое уравнение и система в целом идентифицированы. Для определения параметров такой системы применяется косвенный метод наименьших квадратов.
 Системы одновременных уравнений С этой целью структурная форма модели преобразуется в приведенную форму: y 1 = δ 11 х1 + δ 12 х2 y 2 = δ 21 х1 + δ 22 х2 в которой коэффициенты при х определяют методом наименьших квадратов. Для нахождения значений δ 11 и δ 12 запишем систему нормальных уравнений: Σy 1 х1 = δ 11 Σ х12 + δ 12 Σ х1 х2 Σy 1 х2 = δ 11 Σ х1 х2 + δ 12 Σ х22
Системы одновременных уравнений С этой целью структурная форма модели преобразуется в приведенную форму: y 1 = δ 11 х1 + δ 12 х2 y 2 = δ 21 х1 + δ 22 х2 в которой коэффициенты при х определяют методом наименьших квадратов. Для нахождения значений δ 11 и δ 12 запишем систему нормальных уравнений: Σy 1 х1 = δ 11 Σ х12 + δ 12 Σ х1 х2 Σy 1 х2 = δ 11 Σ х1 х2 + δ 12 Σ х22
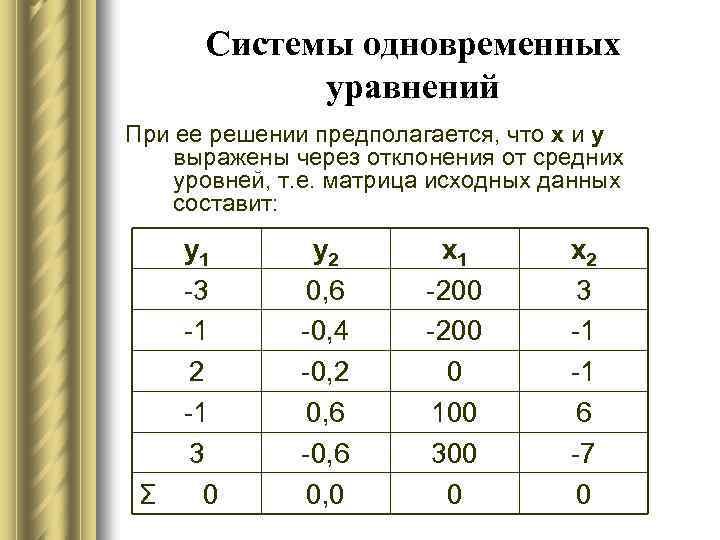 Системы одновременных уравнений При ее решении предполагается, что х и у выражены через отклонения от средних уровней, т. е. матрица исходных данных составит: y 1 -3 -1 2 -1 3 Σ 0 y 2 0, 6 -0, 4 -0, 2 0, 6 -0, 6 0, 0 х1 -200 0 100 300 0 х2 3 -1 -1 6 -7 0
Системы одновременных уравнений При ее решении предполагается, что х и у выражены через отклонения от средних уровней, т. е. матрица исходных данных составит: y 1 -3 -1 2 -1 3 Σ 0 y 2 0, 6 -0, 4 -0, 2 0, 6 -0, 6 0, 0 х1 -200 0 100 300 0 х2 3 -1 -1 6 -7 0
 Системы одновременных уравнений Применительно к таким исходным данным находим необходимые суммы: Σy 1 х1 = 1600 Σ х12 = 180 000 Σ х1 х2 = -1900 Σy 1 х2 = -37 Σ х22 = 96
Системы одновременных уравнений Применительно к таким исходным данным находим необходимые суммы: Σy 1 х1 = 1600 Σ х12 = 180 000 Σ х1 х2 = -1900 Σy 1 х2 = -37 Σ х22 = 96
 Системы одновременных уравнений Система нормальных уравнений: 1600 = 180 000 δ 11 – 1900 δ 12 - 37 = - 1900 δ 11 + 96 δ 12 Решая ее, получим: δ 11 = 0, 00609 δ 12 = - 0, 26481 Итак, имеем y 1 = 0, 00609 х1 – 0, 26481 х2
Системы одновременных уравнений Система нормальных уравнений: 1600 = 180 000 δ 11 – 1900 δ 12 - 37 = - 1900 δ 11 + 96 δ 12 Решая ее, получим: δ 11 = 0, 00609 δ 12 = - 0, 26481 Итак, имеем y 1 = 0, 00609 х1 – 0, 26481 х2
 Системы одновременных уравнений Аналогично строим систему нормальных уравнений для определения коэффициентов δ 21 и δ 22 : Σy 2 х1 = δ 21 Σ х12 + δ 22 Σ х1 х2 Σy 2 х2 = δ 21 Σ х1 х2 + δ 22 Σ х22 Σy 2 х1 = - 160 Σy 2 х2 = 10, 2 - 160 = 180 000 δ 21 – 1900 δ 22 10, 2 = - 1900 δ 21 + 96 δ 22
Системы одновременных уравнений Аналогично строим систему нормальных уравнений для определения коэффициентов δ 21 и δ 22 : Σy 2 х1 = δ 21 Σ х12 + δ 22 Σ х1 х2 Σy 2 х2 = δ 21 Σ х1 х2 + δ 22 Σ х22 Σy 2 х1 = - 160 Σy 2 х2 = 10, 2 - 160 = 180 000 δ 21 – 1900 δ 22 10, 2 = - 1900 δ 21 + 96 δ 22
 Системы одновременных уравнений Следовательно, δ 21 = 0, 00029 δ 22 = 0, 11207, тогда второе уравнение примет вид: y 2 = 0, 00029 х1 – 0, 11207 х2
Системы одновременных уравнений Следовательно, δ 21 = 0, 00029 δ 22 = 0, 11207, тогда второе уравнение примет вид: y 2 = 0, 00029 х1 – 0, 11207 х2
 Системы одновременных уравнений Приведенная форма модели имеет вид: y 1 = 0, 00609 х1 – 0, 26481 х2 y 2 = 0, 00029 х1 + 0, 11207 х2 Из приведенной формы модели определяем коэффициенты структурной модели: y 1 = 0, 00609 х1 – 0, 26481 х2 х2 = y 2 - 0, 00029 х1 0, 11207
Системы одновременных уравнений Приведенная форма модели имеет вид: y 1 = 0, 00609 х1 – 0, 26481 х2 y 2 = 0, 00029 х1 + 0, 11207 х2 Из приведенной формы модели определяем коэффициенты структурной модели: y 1 = 0, 00609 х1 – 0, 26481 х2 х2 = y 2 - 0, 00029 х1 0, 11207
 Системы одновременных уравнений y 1 = 0, 00609 х1 – 0, 26481 y 2 - 0, 00029 х1 0, 11207 = -2, 36290 y 2 + 0, 00678 х1 Итак, первое уравнение СФМ: y 1 = - 2, 36290 y 2 + 0, 00678 х1 =
Системы одновременных уравнений y 1 = 0, 00609 х1 – 0, 26481 y 2 - 0, 00029 х1 0, 11207 = -2, 36290 y 2 + 0, 00678 х1 Итак, первое уравнение СФМ: y 1 = - 2, 36290 y 2 + 0, 00678 х1 =
 Системы одновременных уравнений y 2 = 0, 00029 х1 + 0, 11207 х2 х1 = y 1 + 0, 026481 х2 0, 00609
Системы одновременных уравнений y 2 = 0, 00029 х1 + 0, 11207 х2 х1 = y 1 + 0, 026481 х2 0, 00609
 Системы одновременных уравнений y 2 = 0, 00029 y 1 + 0, 26481 х2 0, 00609 + 0, 11207 х2 = = 0, 04762 y 1 + 0, 12468 х2 Второе уравнение СФМ: y 2 = 0, 04762 y 1 + 0, 12468 х2
Системы одновременных уравнений y 2 = 0, 00029 y 1 + 0, 26481 х2 0, 00609 + 0, 11207 х2 = = 0, 04762 y 1 + 0, 12468 х2 Второе уравнение СФМ: y 2 = 0, 04762 y 1 + 0, 12468 х2
 Системы одновременных уравнений Итак, структурная форма модели имеет вид: y 1 = - 2, 36290 y 2 + 0, 00678 х1+ ε 1 y 2 = 0, 04762 y 1 + 0, 12468 х2 + ε 2
Системы одновременных уравнений Итак, структурная форма модели имеет вид: y 1 = - 2, 36290 y 2 + 0, 00678 х1+ ε 1 y 2 = 0, 04762 y 1 + 0, 12468 х2 + ε 2
 Системы одновременных уравнений Пример 4. Рассматривается следующая модель: Ct = a 1+ b 11 Yt + b 12 Ct-1+ U 1 (функция потребления) It = a 2+ b 21 rt + b 22 It-1+ U 2 (функция инвестиций) rt = a 3+ b 31 Yt + b 32 Mt + U 3 (функция денежного рынка) Yt = C t + I t + Gt (тождество дохода)
Системы одновременных уравнений Пример 4. Рассматривается следующая модель: Ct = a 1+ b 11 Yt + b 12 Ct-1+ U 1 (функция потребления) It = a 2+ b 21 rt + b 22 It-1+ U 2 (функция инвестиций) rt = a 3+ b 31 Yt + b 32 Mt + U 3 (функция денежного рынка) Yt = C t + I t + Gt (тождество дохода)
 Системы одновременных уравнений Требуется: 1. В предположении, что имеются временные ряды данных по всем переменным модели, предложите способ оценки ее параметров. 2. Как изменится ваш ответ на вопрос 1, если из модели исключить тождество дохода?
Системы одновременных уравнений Требуется: 1. В предположении, что имеются временные ряды данных по всем переменным модели, предложите способ оценки ее параметров. 2. Как изменится ваш ответ на вопрос 1, если из модели исключить тождество дохода?
 Системы одновременных уравнений Решение: 1. Модель представляет собой систему одновременных уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое уравнение на идентификацию. Модель включает четыре эндогенные переменные (Ct, It, Yt, rt ) и четыре предопределенные переменные – две экзогенные переменные (Mt , Gt ) и две лаговые эндогенные переменные (Ct-1 , It-1).
Системы одновременных уравнений Решение: 1. Модель представляет собой систему одновременных уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое уравнение на идентификацию. Модель включает четыре эндогенные переменные (Ct, It, Yt, rt ) и четыре предопределенные переменные – две экзогенные переменные (Mt , Gt ) и две лаговые эндогенные переменные (Ct-1 , It-1).
 Системы одновременных уравнений Проверим необходимое условие идентификации для уравнений модели. 1 уравнение. Это уравнение включает две эндогенные переменные (Ct, Yt ) и одну предопределенную переменную (Ct-1 ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1 > 2. уравнение сверхидентифицировано.
Системы одновременных уравнений Проверим необходимое условие идентификации для уравнений модели. 1 уравнение. Это уравнение включает две эндогенные переменные (Ct, Yt ) и одну предопределенную переменную (Ct-1 ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1 > 2. уравнение сверхидентифицировано.
 Системы одновременных уравнений 2 уравнение. Это уравнение включает две эндогенные переменные (It, rt) и не включает три предопределенные переменные. Как и первое уравнение, оно сверхидентифицировано. 3 уравнение. Уравнение 3 тоже включает две эндогенные переменные (Yt, rt) и не включает три предопределенные переменные. Это уравнение сверхидентифицировано.
Системы одновременных уравнений 2 уравнение. Это уравнение включает две эндогенные переменные (It, rt) и не включает три предопределенные переменные. Как и первое уравнение, оно сверхидентифицировано. 3 уравнение. Уравнение 3 тоже включает две эндогенные переменные (Yt, rt) и не включает три предопределенные переменные. Это уравнение сверхидентифицировано.
 Системы одновременных уравнений 4 уравнение. Уравнение 4 представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет. Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
Системы одновременных уравнений 4 уравнение. Уравнение 4 представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет. Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
 Системы одновременных уравнений Ct Yt Ct-1 It rt It-1 Mt Gt 1 уравнение -1 b 12 0 0 0 2 уравнение 0 0 0 -1 b 22 0 0 3 уравнение 0 b 31 0 0 -1 0 b 32 0 4 уравнение 1 -1 0 0 0 1
Системы одновременных уравнений Ct Yt Ct-1 It rt It-1 Mt Gt 1 уравнение -1 b 12 0 0 0 2 уравнение 0 0 0 -1 b 22 0 0 3 уравнение 0 b 31 0 0 -1 0 b 32 0 4 уравнение 1 -1 0 0 0 1
 Системы одновременных уравнений В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть равен числу эндогенных переменных модели минус 1, т. е. 4 -1=3. 1 уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
Системы одновременных уравнений В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть равен числу эндогенных переменных модели минус 1, т. е. 4 -1=3. 1 уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
 Системы одновременных уравнений А = -1 b 21 0 -1 1 0 b 22 0 0 0 b 32 0 0 0 1 Ее ранг равен 3, так как определитель квадратной подматрицы 3 х3 этой матрицы не равен нулю: -1 b 21 0 Det A´= 0 -1 0 ≠ 0 1
Системы одновременных уравнений А = -1 b 21 0 -1 1 0 b 22 0 0 0 b 32 0 0 0 1 Ее ранг равен 3, так как определитель квадратной подматрицы 3 х3 этой матрицы не равен нулю: -1 b 21 0 Det A´= 0 -1 0 ≠ 0 1
 Системы одновременных уравнений Достаточное условие идентификации для 1 уравнения выполняется. 2 уравнение. Выпишем матрицу коэффициентов переменных, не входящих в уравнение: -1 b 12 0 0 А = 0 b 31 0 b 32 0 1 -1 0 0 1 при
Системы одновременных уравнений Достаточное условие идентификации для 1 уравнения выполняется. 2 уравнение. Выпишем матрицу коэффициентов переменных, не входящих в уравнение: -1 b 12 0 0 А = 0 b 31 0 b 32 0 1 -1 0 0 1 при
 Системы одновременных уравнений Ее ранг равен 3, так как определитель квадратной подматрицы 3 х3 этой матрицы не равен нулю: -1 b 21 0 Det. A´ = 0 -1 0 ≠ 0 1 Достаточное условие идентификации для 2 уравнения выполняется.
Системы одновременных уравнений Ее ранг равен 3, так как определитель квадратной подматрицы 3 х3 этой матрицы не равен нулю: -1 b 21 0 Det. A´ = 0 -1 0 ≠ 0 1 Достаточное условие идентификации для 2 уравнения выполняется.
 Системы одновременных уравнений 3 уравнение. Выпишем матрицу коэффициентов при переменных, не входящих в уравнение: -1 b 12 0 А = 0 0 -1 1 0 0 b 22 0 0 1
Системы одновременных уравнений 3 уравнение. Выпишем матрицу коэффициентов при переменных, не входящих в уравнение: -1 b 12 0 А = 0 0 -1 1 0 0 b 22 0 0 1
 Системы одновременных уравнений Ее ранг равен 3, так как определитель квадратной подматрицы 3 х3 этой матрицы не равен нулю: -1 0 0 Det. A´ = 0 -1 0 ≠ 0 1 1 1 Достаточное условие идентификации для 3 уравнения выполняется.
Системы одновременных уравнений Ее ранг равен 3, так как определитель квадратной подматрицы 3 х3 этой матрицы не равен нулю: -1 0 0 Det. A´ = 0 -1 0 ≠ 0 1 1 1 Достаточное условие идентификации для 3 уравнения выполняется.
 Системы одновременных уравнений Таким образом, все уравнения модели сверхидентифицированы. Для оценки параметров каждого из уравнений будем применять двухшаговый МНК. Шаг 1. Запишем приведенную форму модели в общем виде: Ct = A 1+ A 2 Ct-1 + A 3 It-1 + A 4 Mt + A 5 Gt + V 1 ; It = B 1+ B 2 Ct-1 + B 3 It-1 + B 4 Mt + B 5 Gt + V 2 ; Yt = D 1+ D 2 Ct-1 + D 3 It-1 + D 4 Mt + D 5 Gt + V 3 ; rt = E 1+ E 2 Ct-1 + E 3 It-1 + E 4 Mt + E 5 Gt + V 4 ; где V 1, V 2 , V 3 , V 4 - случайные ошибки.
Системы одновременных уравнений Таким образом, все уравнения модели сверхидентифицированы. Для оценки параметров каждого из уравнений будем применять двухшаговый МНК. Шаг 1. Запишем приведенную форму модели в общем виде: Ct = A 1+ A 2 Ct-1 + A 3 It-1 + A 4 Mt + A 5 Gt + V 1 ; It = B 1+ B 2 Ct-1 + B 3 It-1 + B 4 Mt + B 5 Gt + V 2 ; Yt = D 1+ D 2 Ct-1 + D 3 It-1 + D 4 Mt + D 5 Gt + V 3 ; rt = E 1+ E 2 Ct-1 + E 3 It-1 + E 4 Mt + E 5 Gt + V 4 ; где V 1, V 2 , V 3 , V 4 - случайные ошибки.
 Системы одновременных уравнений Определим параметры каждого из приведенных выше уравнений в отдельности обычным МНК. Затем найдем расчетные значения эндогенных переменных Ŷt, řt, используемых в правой части структурной модели, подставляя в каждое уравнение приведенной формы соответствующее значение предопределенных переменных.
Системы одновременных уравнений Определим параметры каждого из приведенных выше уравнений в отдельности обычным МНК. Затем найдем расчетные значения эндогенных переменных Ŷt, řt, используемых в правой части структурной модели, подставляя в каждое уравнение приведенной формы соответствующее значение предопределенных переменных.
 Системы одновременных уравнений Шаг 2. В исходных структурных уравнениях заменим эндогенные переменные, выступающие в качестве факторных признаков, их расчетными значениями: Ct = a 1+ b 11 Ŷt + b 12 Ct-1+ U 1* , где U 1* = U 1 + b 11 V 1 ; It = a 2+ b 21 řt + b 22 It-1+ U 2 * , где U 2* = U 2 + b 21 V 2 ; rt = a 3+ b 31 Ŷt + b 32 Mt + U 3* , где U 3* = U 3 + b 31 V 3 Применяя к каждому из полученных уравнений в отдельности обычный МНК, определим структурные параметры a 1 b 12 a 2 b 21 b 22 a 3 b 31 b 32
Системы одновременных уравнений Шаг 2. В исходных структурных уравнениях заменим эндогенные переменные, выступающие в качестве факторных признаков, их расчетными значениями: Ct = a 1+ b 11 Ŷt + b 12 Ct-1+ U 1* , где U 1* = U 1 + b 11 V 1 ; It = a 2+ b 21 řt + b 22 It-1+ U 2 * , где U 2* = U 2 + b 21 V 2 ; rt = a 3+ b 31 Ŷt + b 32 Mt + U 3* , где U 3* = U 3 + b 31 V 3 Применяя к каждому из полученных уравнений в отдельности обычный МНК, определим структурные параметры a 1 b 12 a 2 b 21 b 22 a 3 b 31 b 32
 Системы одновременных уравнений 2. Если из модели исключить тождество дохода, число предопределенных переменных модели уменьшится на 1 (из модели будет исключена переменная Gt). Число эндогенных переменных модели также снизится на единицу – переменная Yt станет экзогенной. В правых частях функции потребления и функции денежного рынка будут находиться только предопределенные переменные.
Системы одновременных уравнений 2. Если из модели исключить тождество дохода, число предопределенных переменных модели уменьшится на 1 (из модели будет исключена переменная Gt). Число эндогенных переменных модели также снизится на единицу – переменная Yt станет экзогенной. В правых частях функции потребления и функции денежного рынка будут находиться только предопределенные переменные.
 Системы одновременных уравнений Функция инвестиций постулирует зависимость эндогенной переменной It от эндогенной переменной rt (которая зависит только от предопределенных переменных) и предопределенной переменной It-1.
Системы одновременных уравнений Функция инвестиций постулирует зависимость эндогенной переменной It от эндогенной переменной rt (которая зависит только от предопределенных переменных) и предопределенной переменной It-1.
 Системы одновременных уравнений Таким образом, мы получим рекурсивную систему. Ее параметры можно оценивать обычным МНК, и нет необходимости исследования системы уравнения на идентификацию.
Системы одновременных уравнений Таким образом, мы получим рекурсивную систему. Ее параметры можно оценивать обычным МНК, и нет необходимости исследования системы уравнения на идентификацию.


