Системы линейных алгебраических уравнений (СЛАУ)


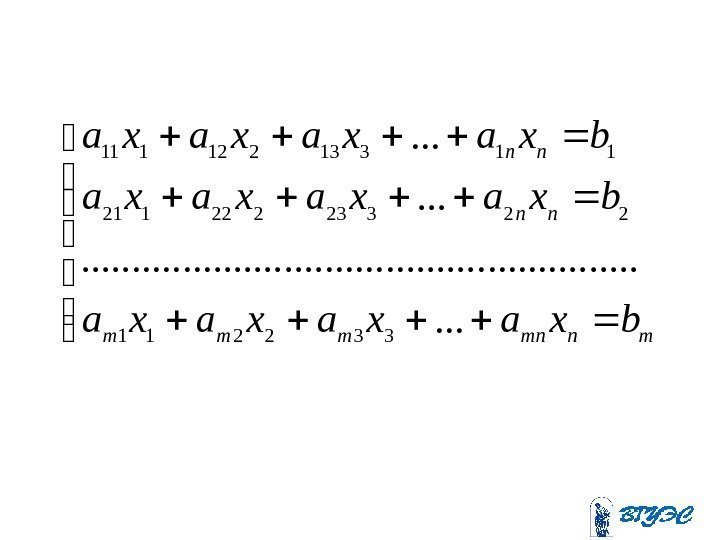













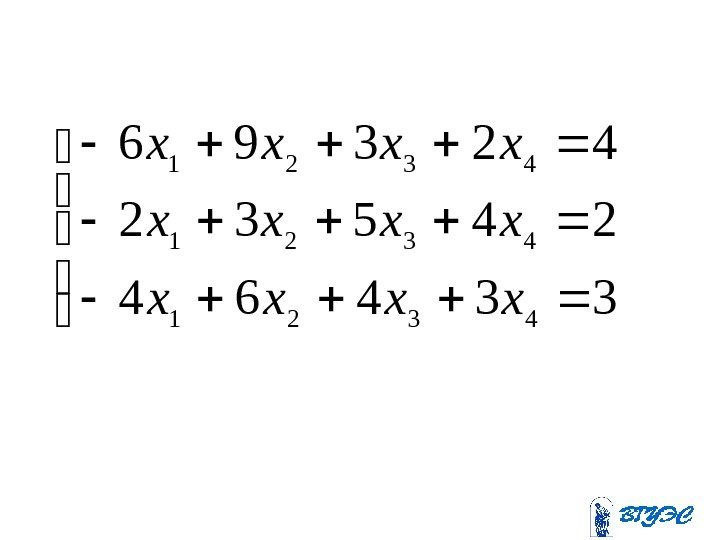





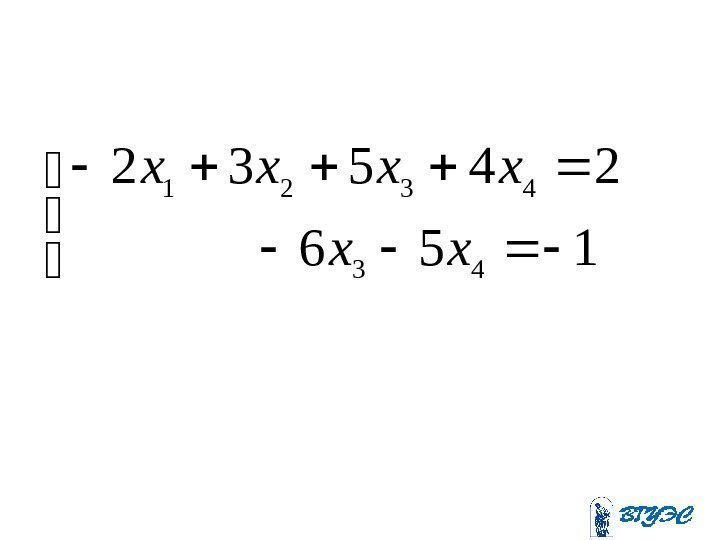
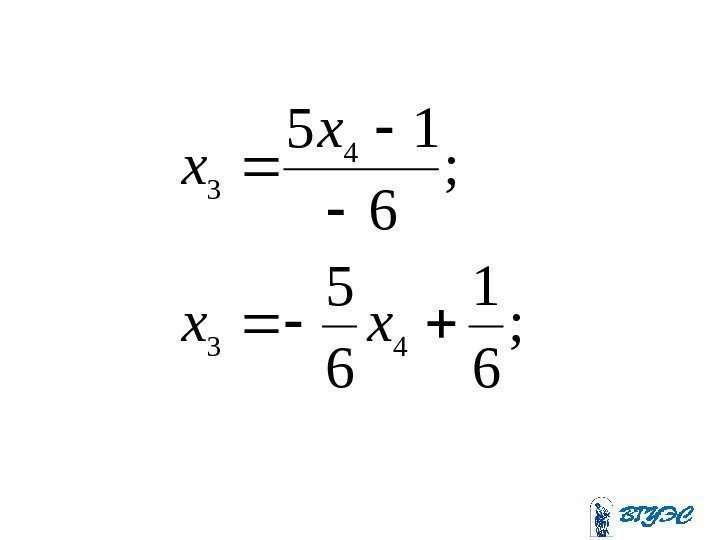
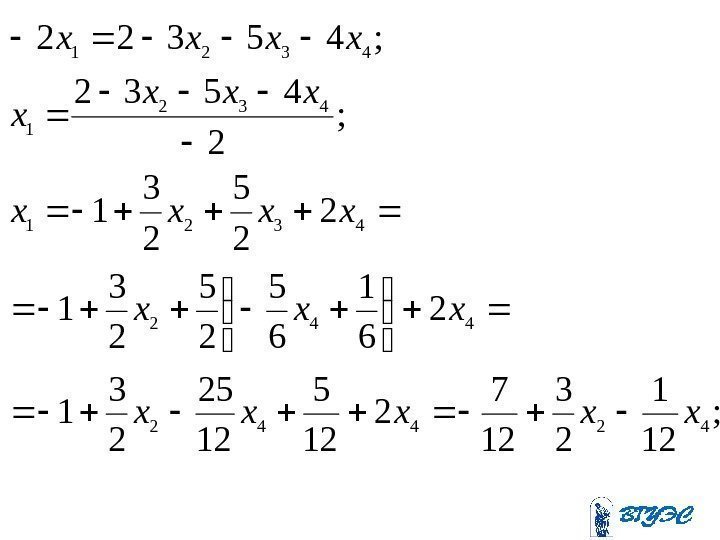
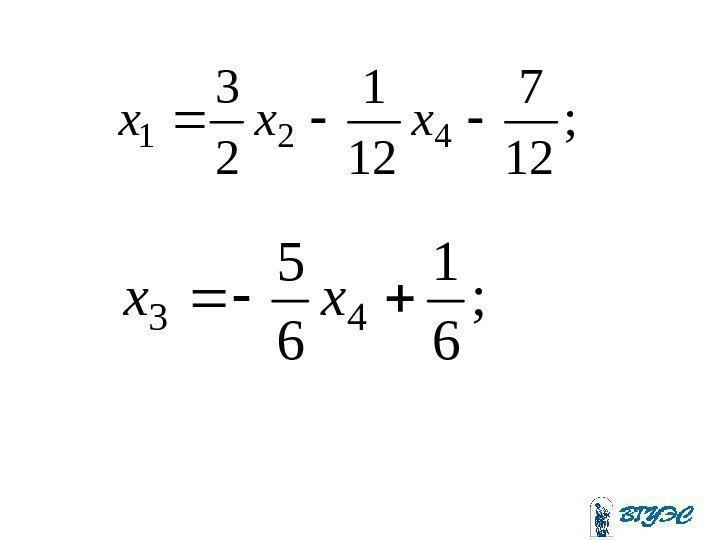
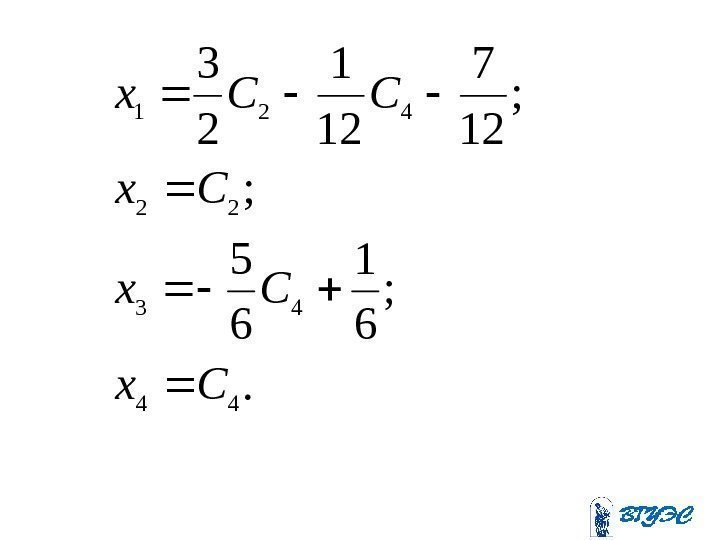

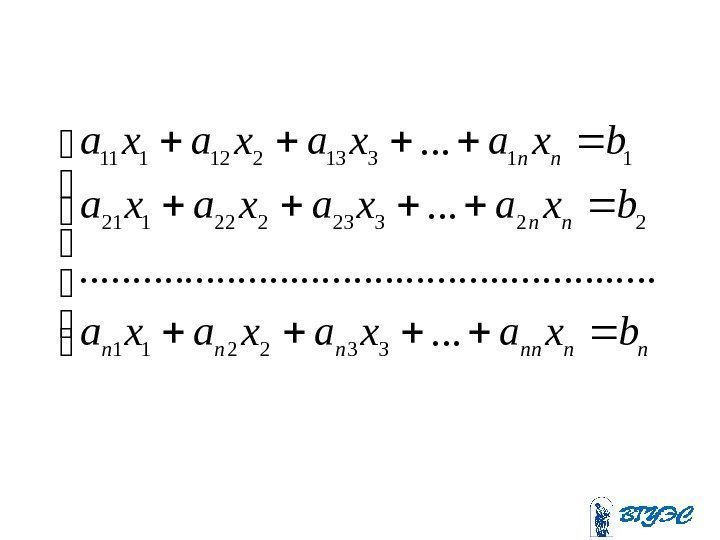
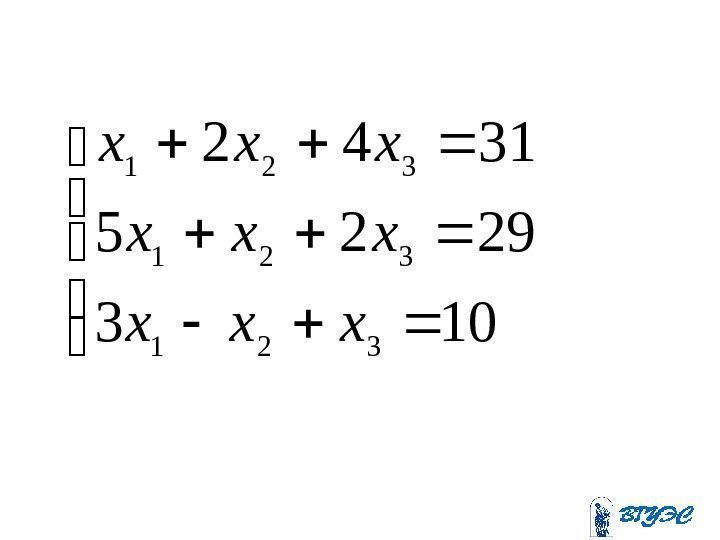
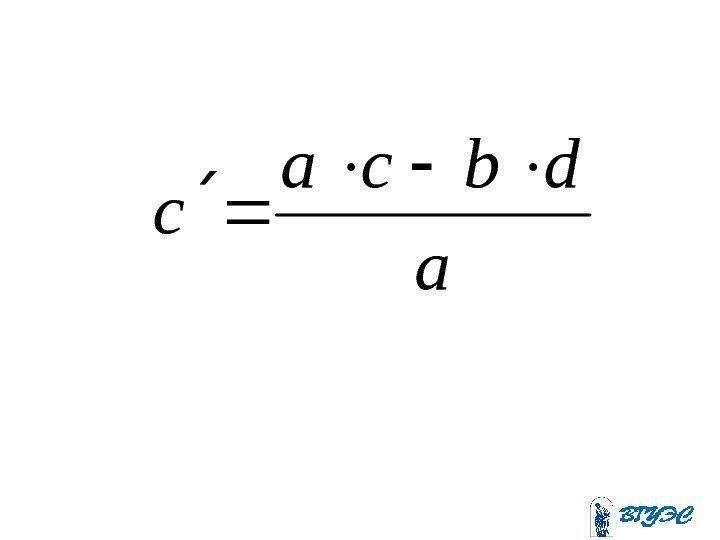
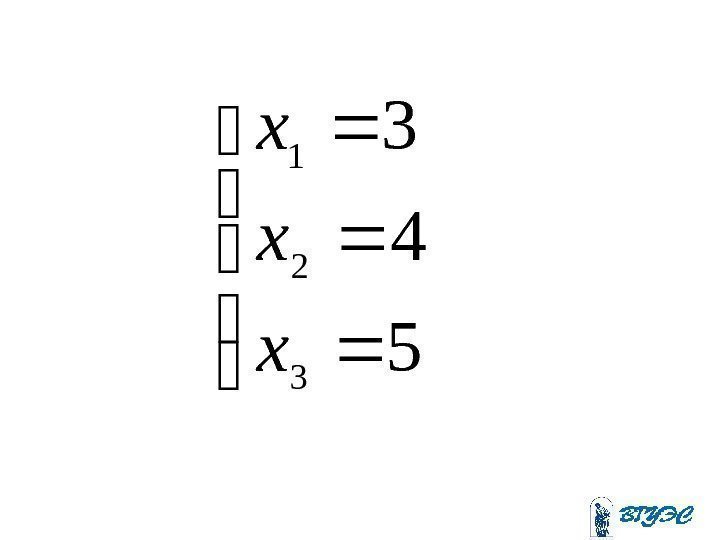
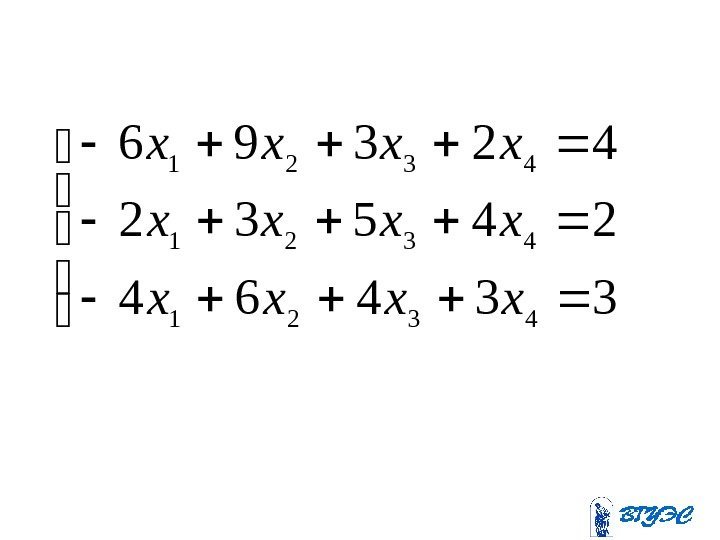
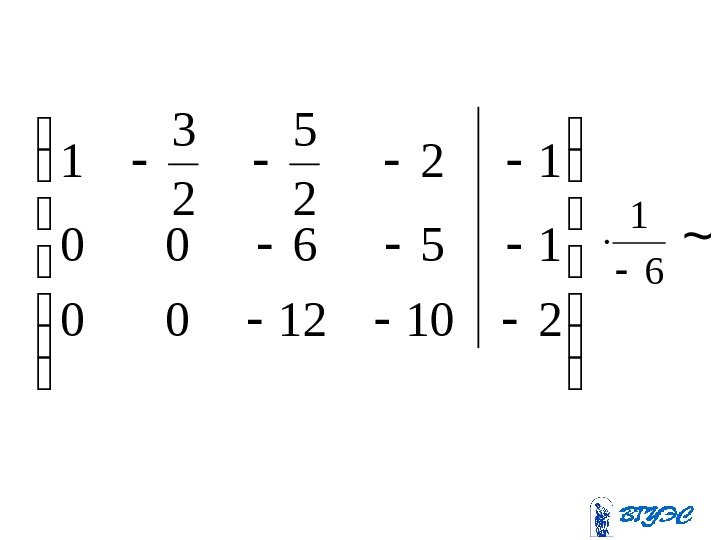
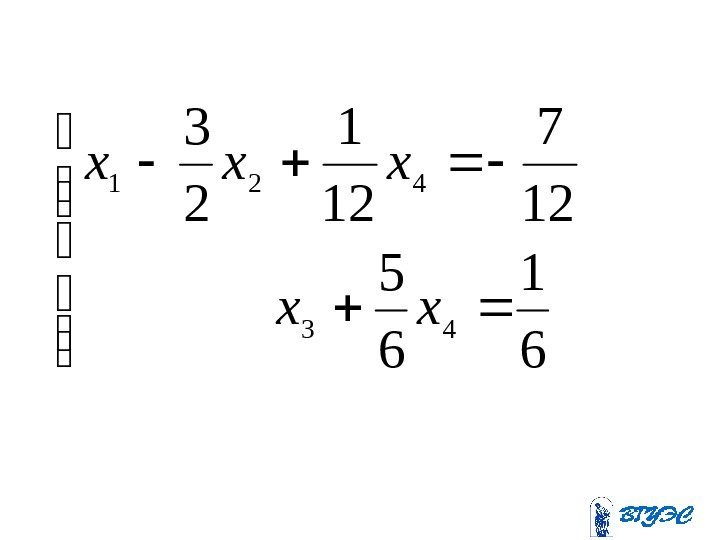
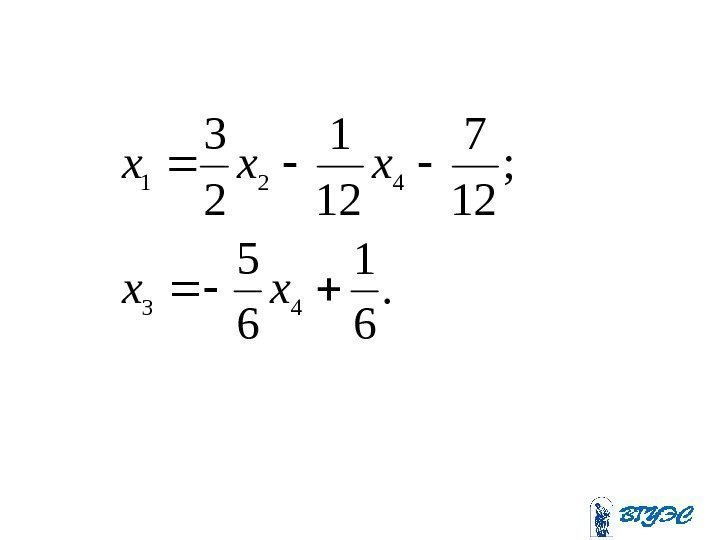
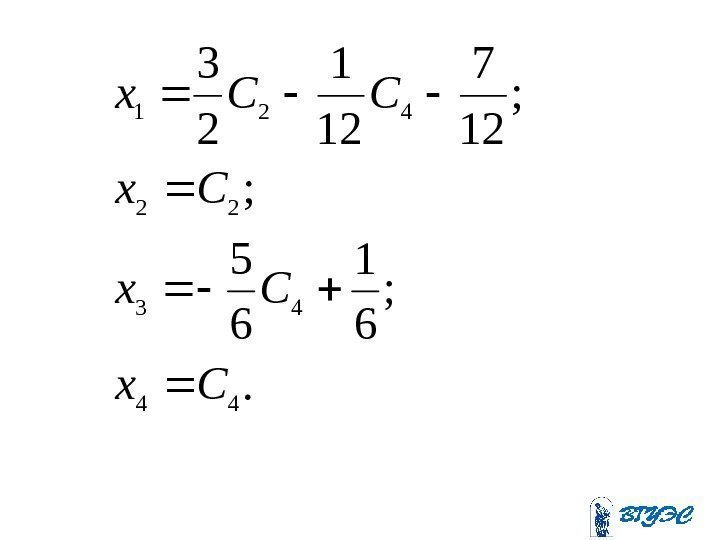


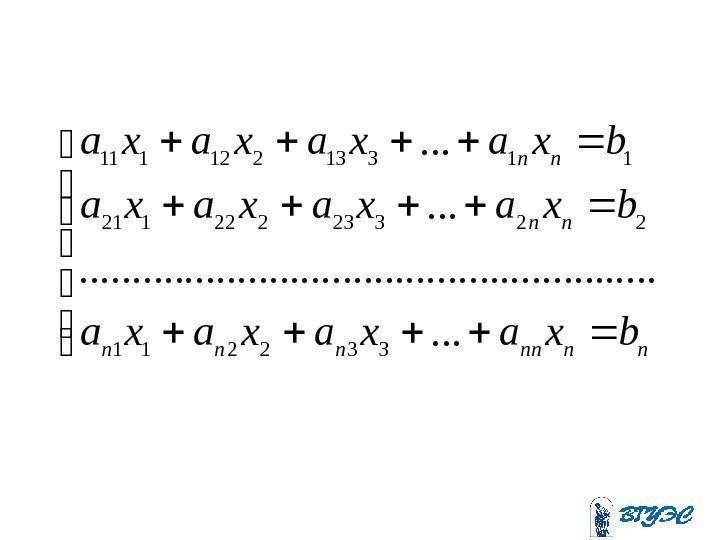

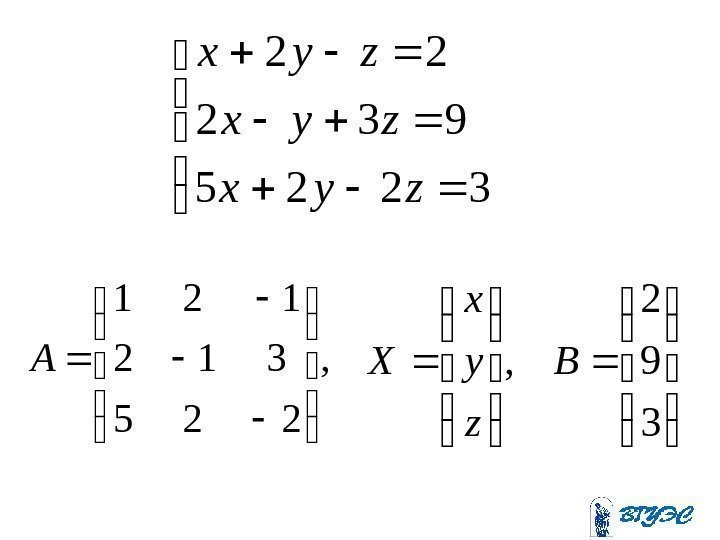
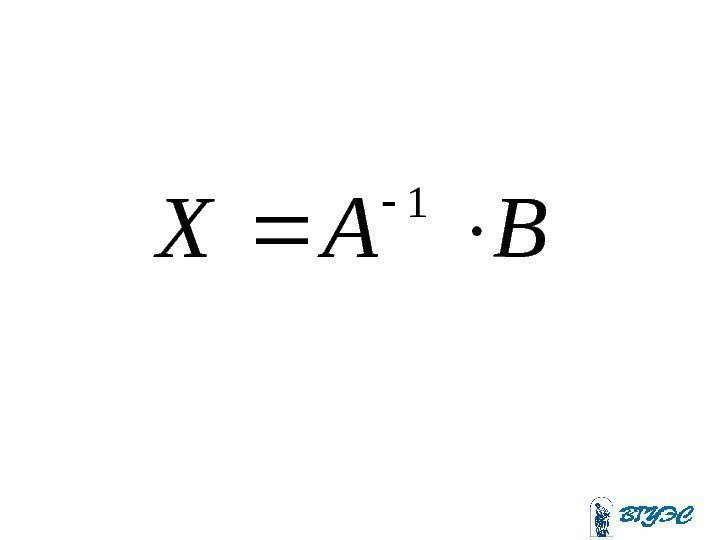
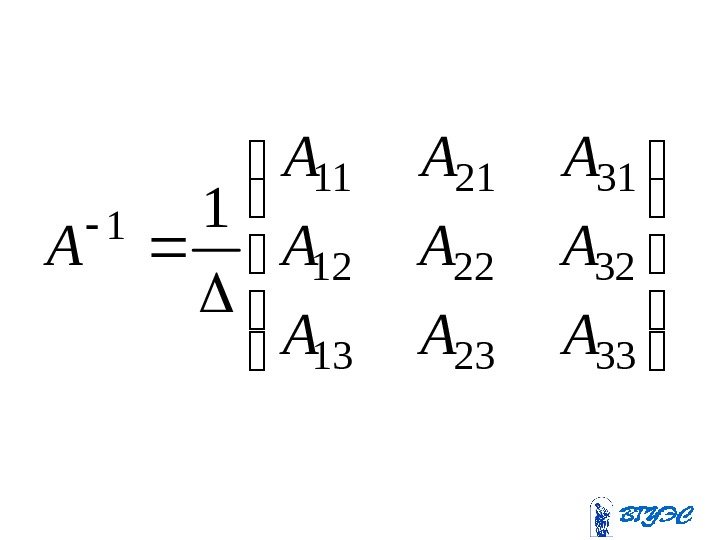
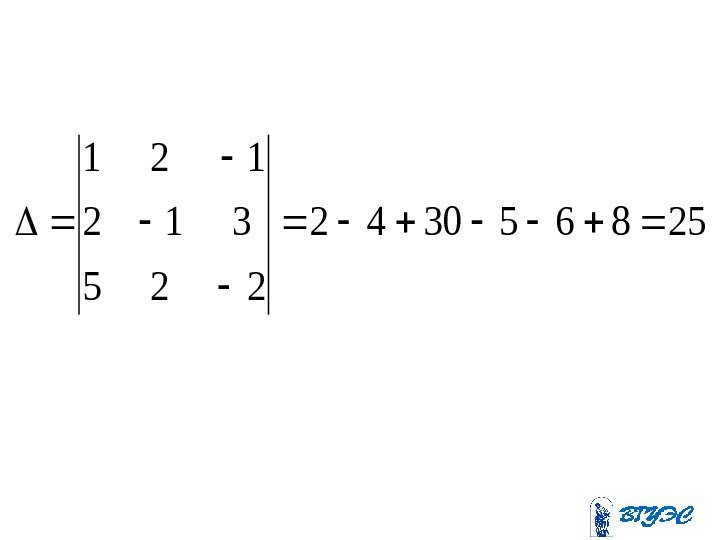
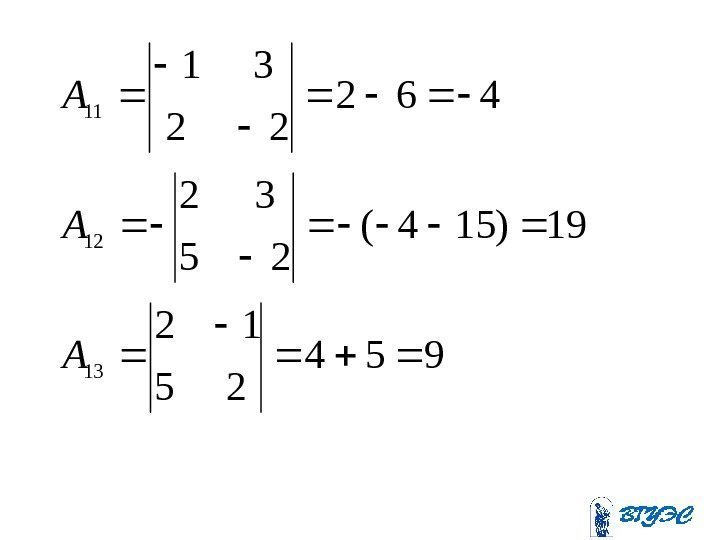
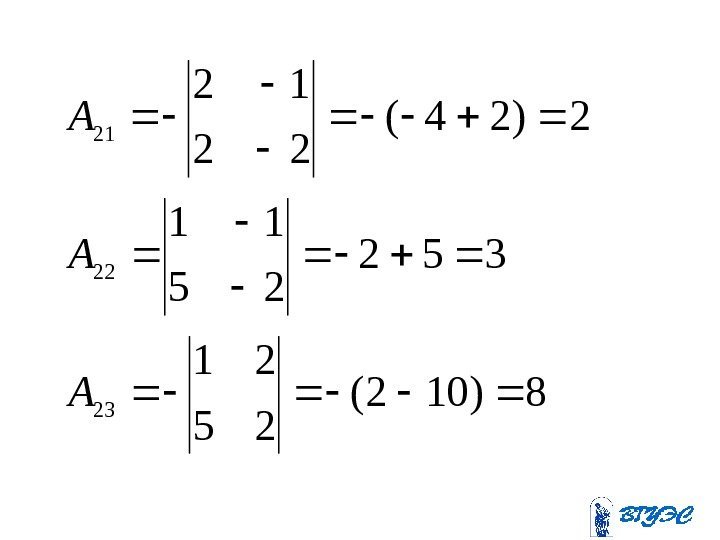
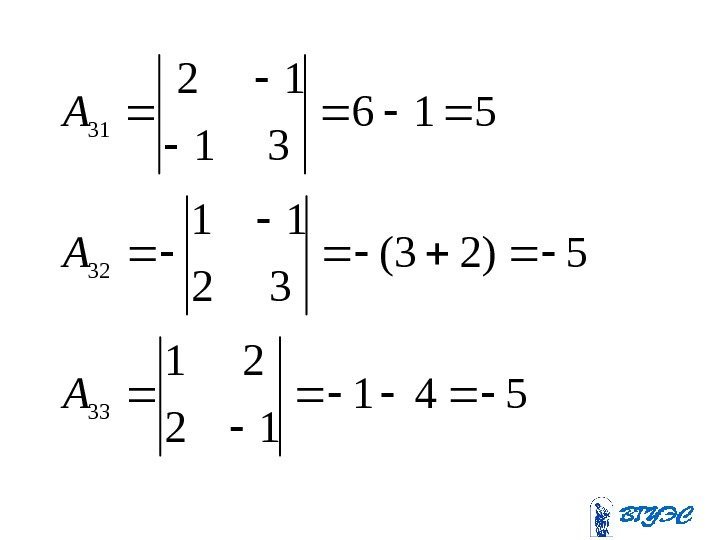
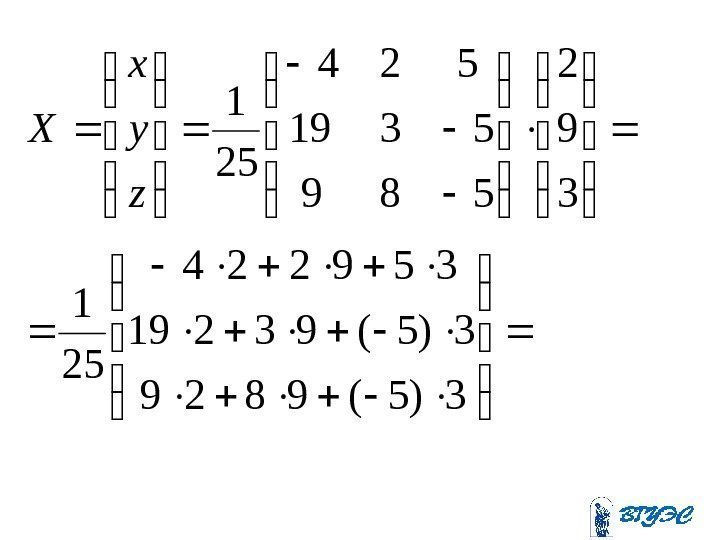
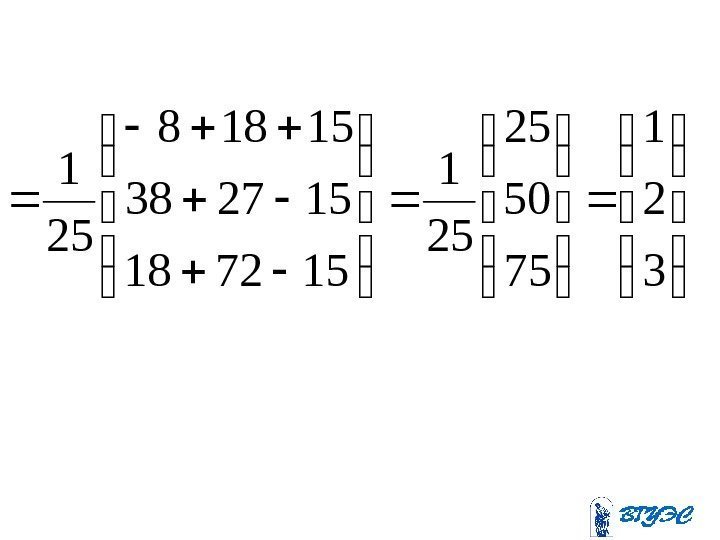
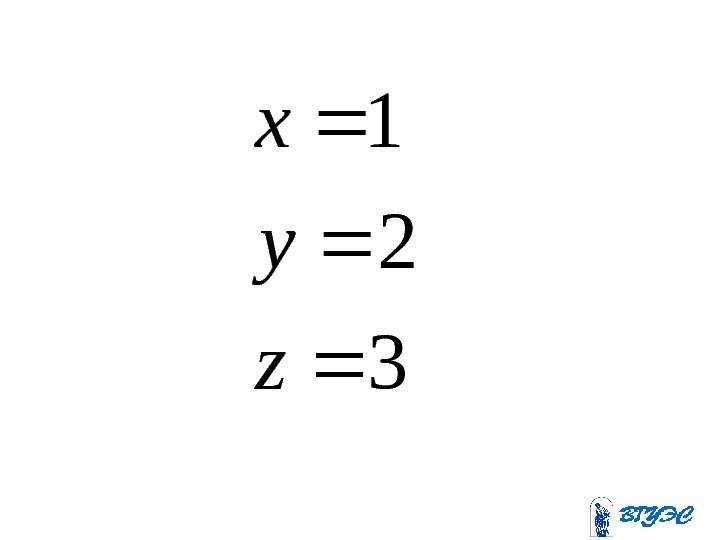


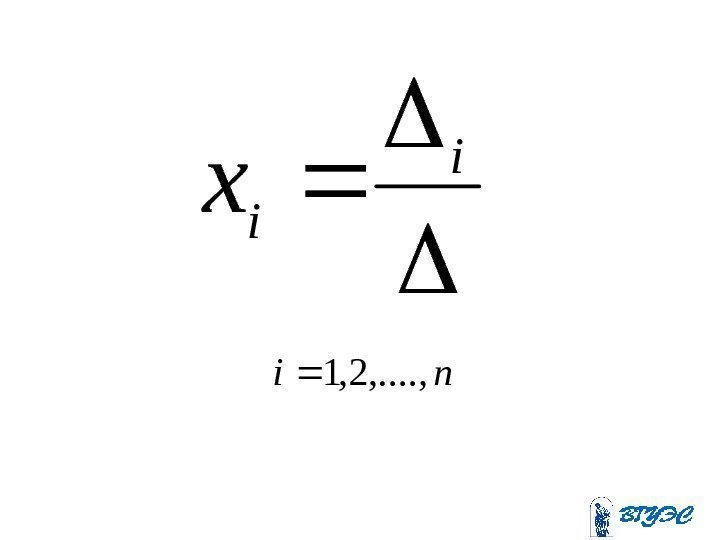


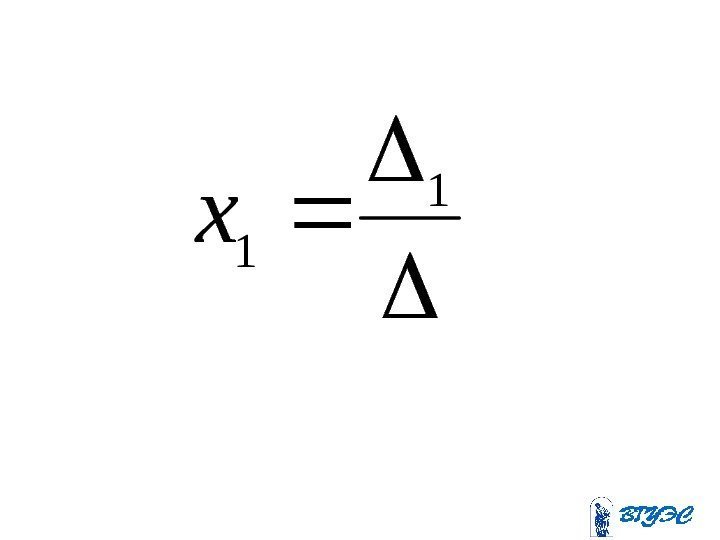
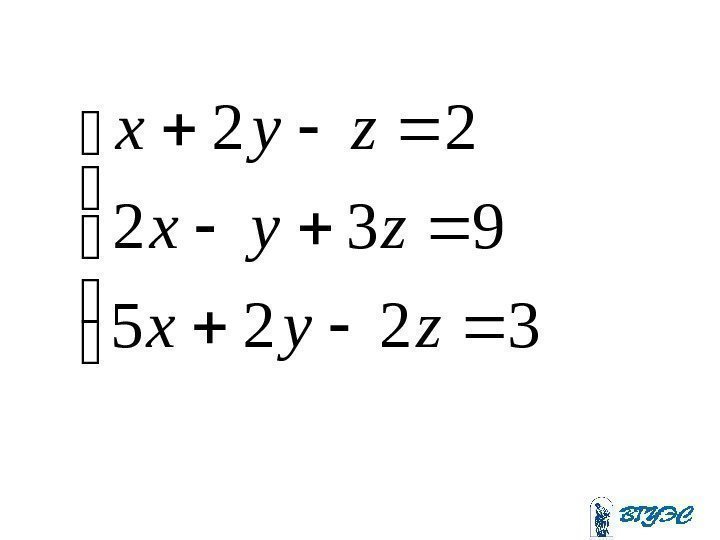
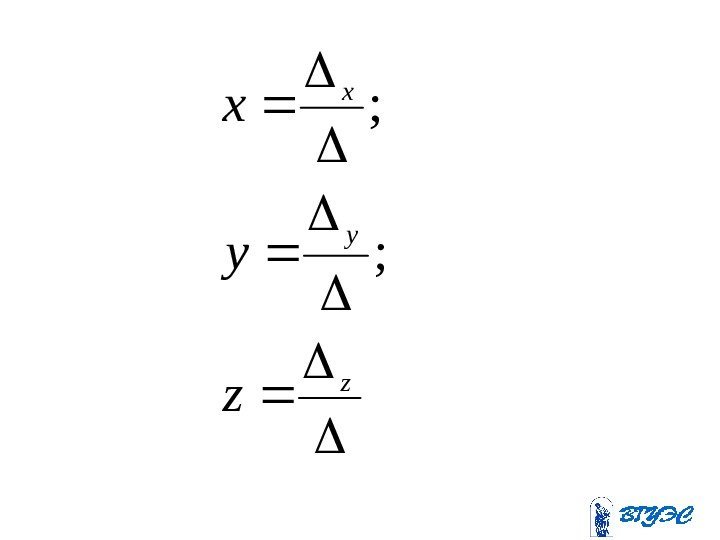
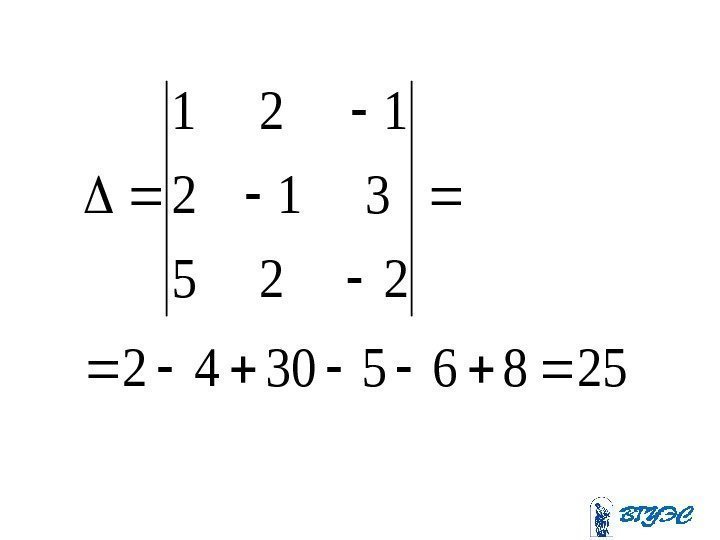
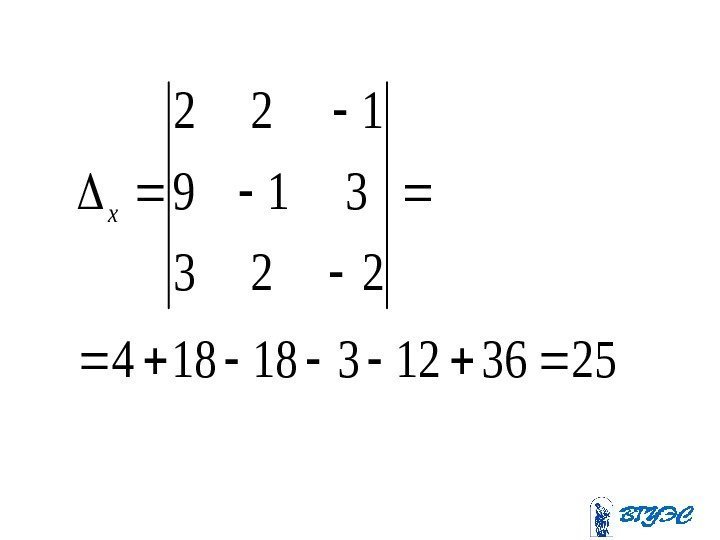
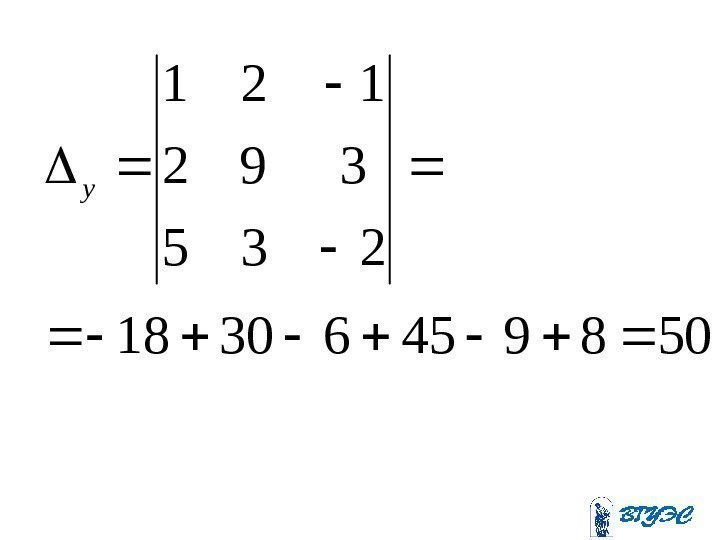
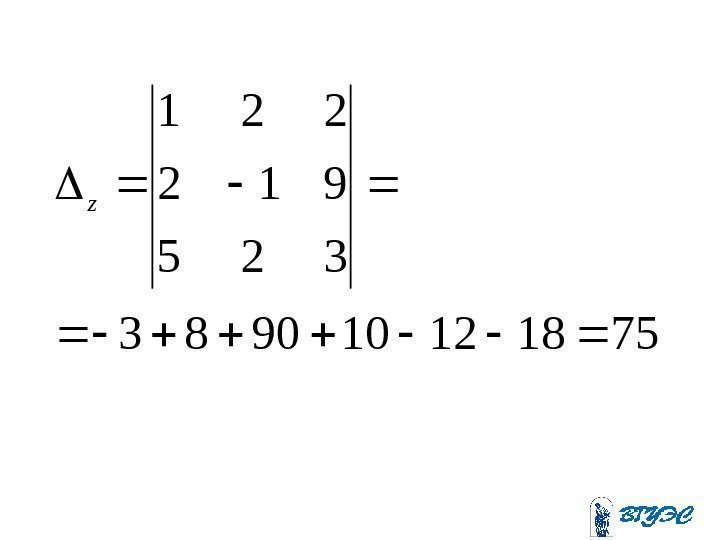
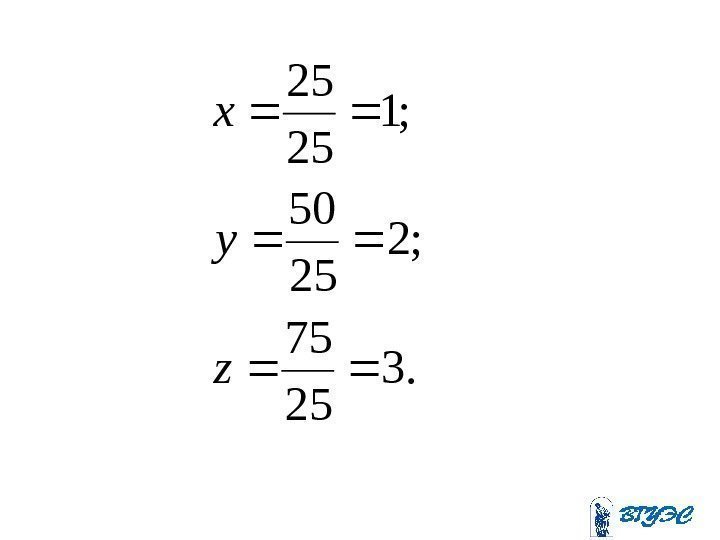

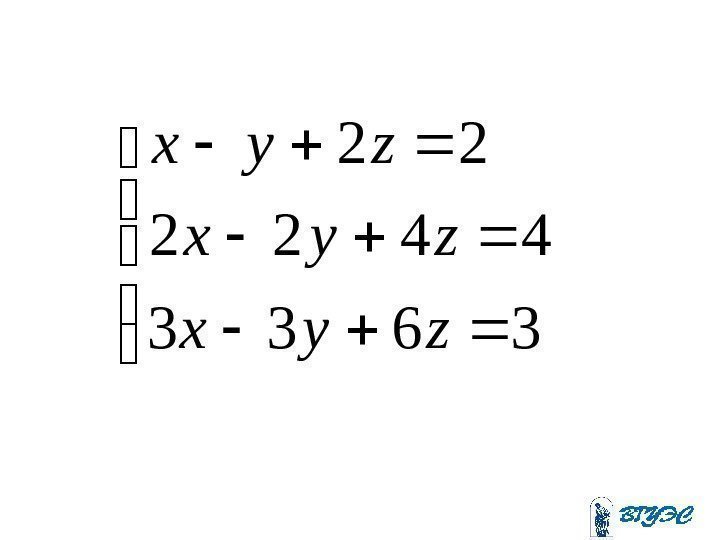
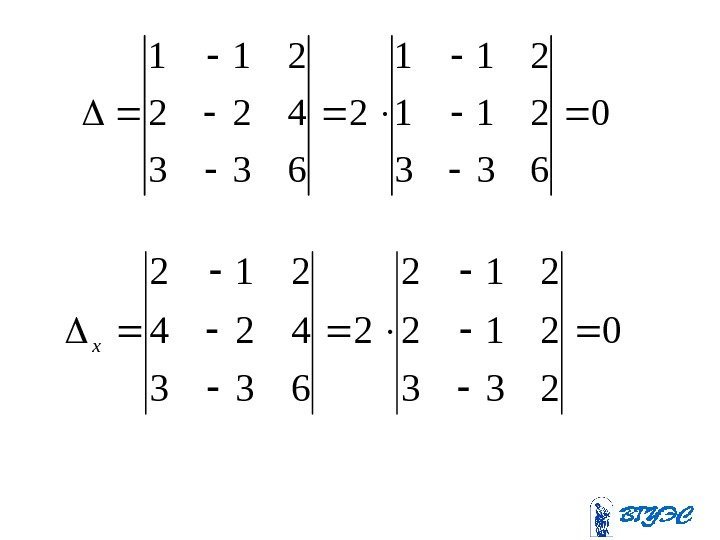


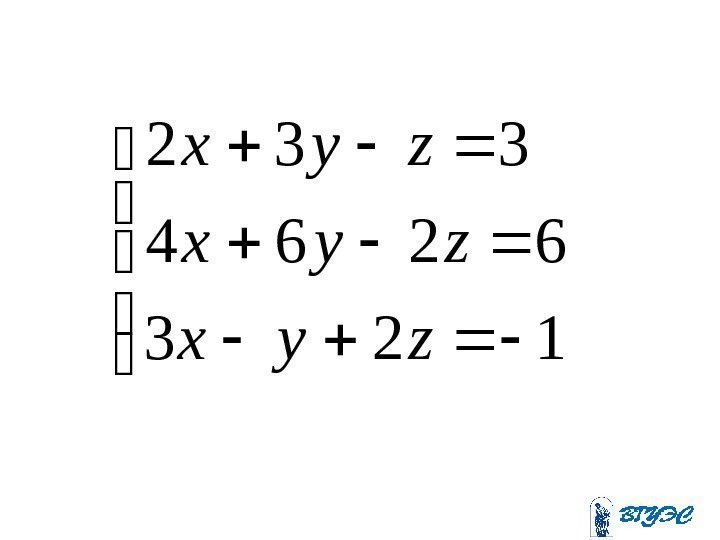
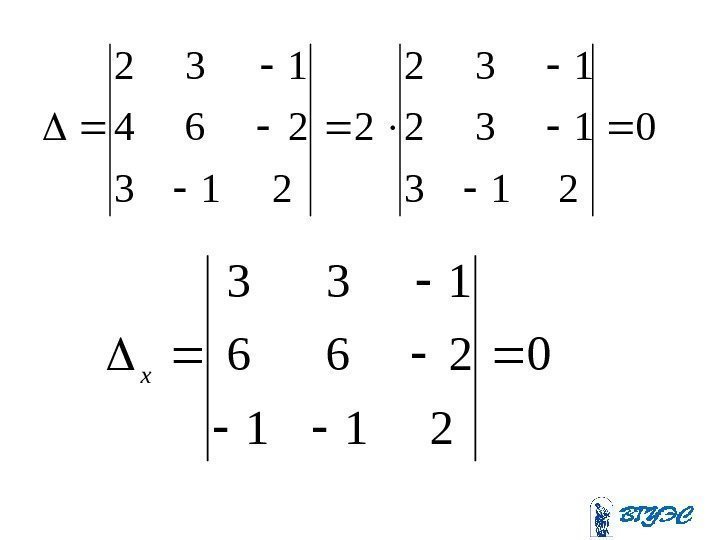
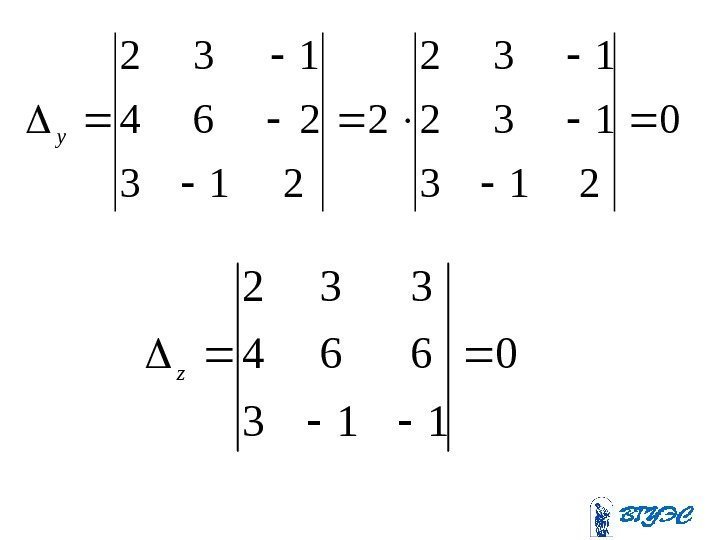

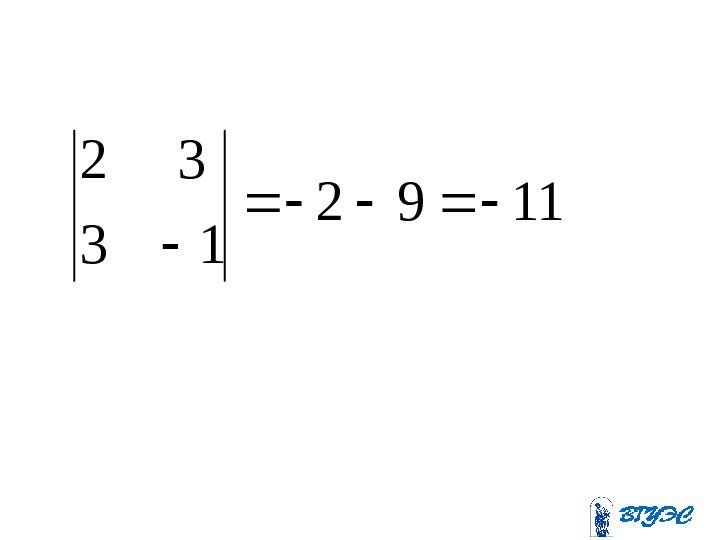
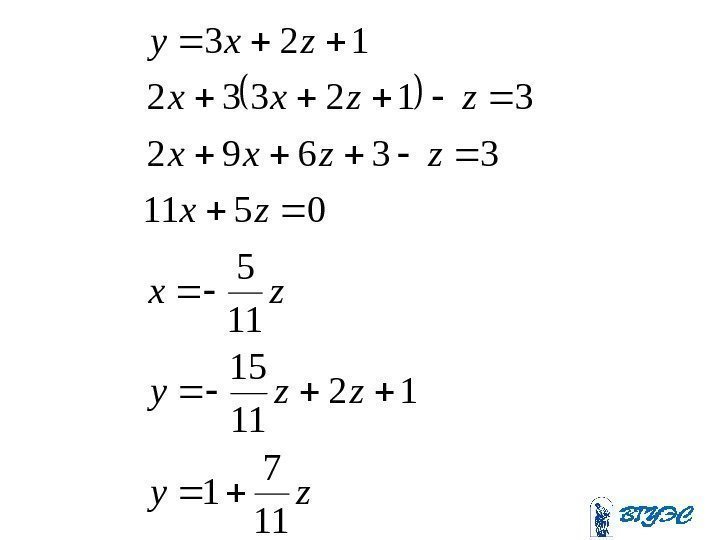
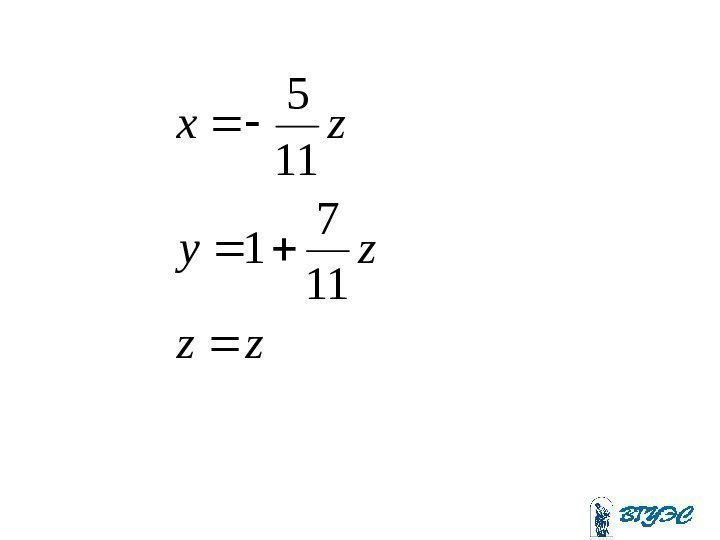


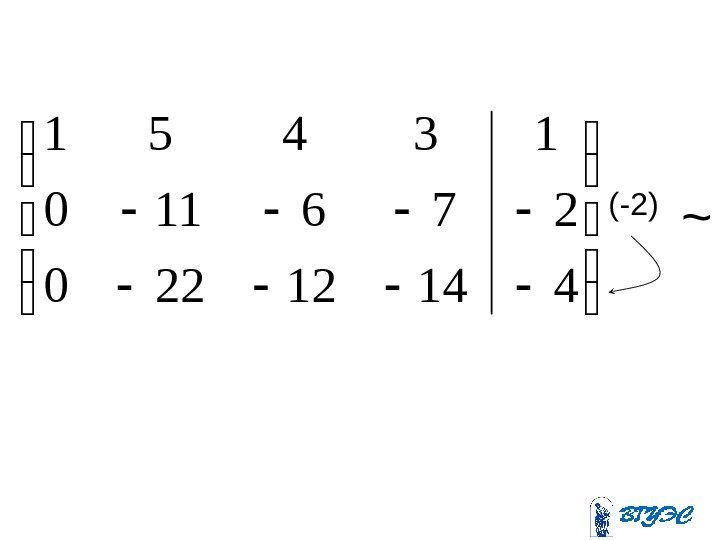


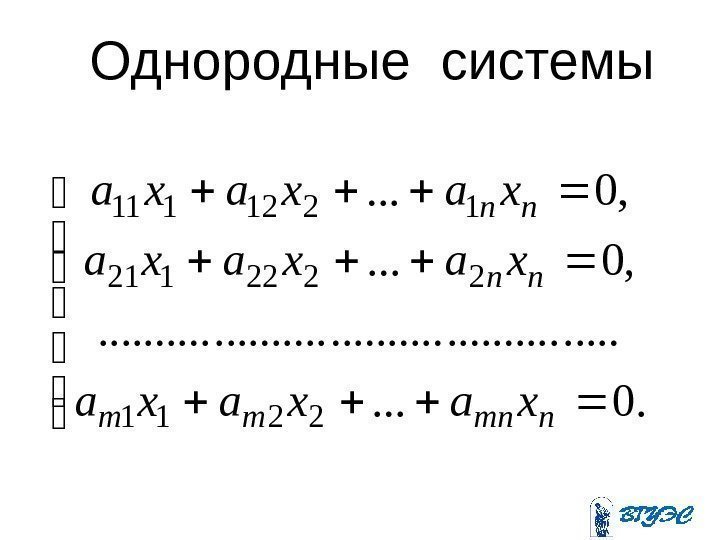

3.sistemy_lineynyh_algebraicheskih_uravneniy.ppt
- Размер: 495.0 Кб
- Автор:
- Количество слайдов: 115
Описание презентации Системы линейных алгебраических уравнений (СЛАУ) по слайдам
 Системы линейных алгебраических уравнений (СЛАУ)
Системы линейных алгебраических уравнений (СЛАУ)
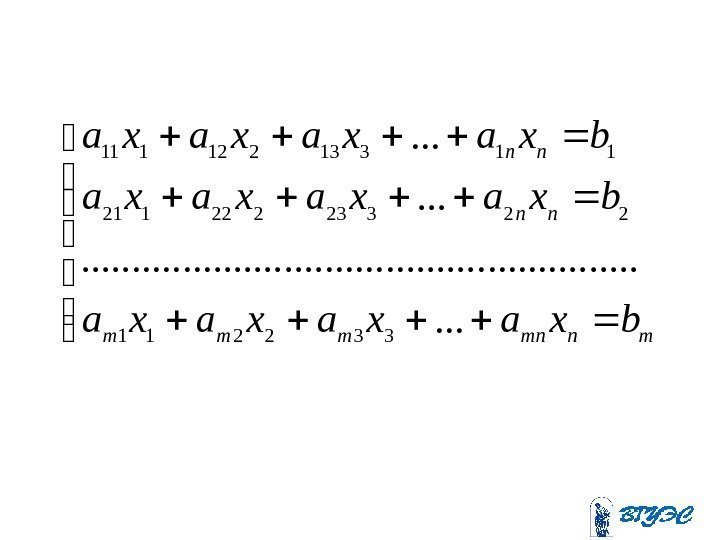 mnmnmmm nn nn bxa. . . xaxaxa. . . . bxa. . . xaxaxa
mnmnmmm nn nn bxa. . . xaxaxa. . . . bxa. . . xaxaxa
 • Здесь — неизвестные; — коэффициенты при неизвестных, где — номер уравнения, — номер неизвестного; — свободные члены (правые части). n xxx, . . . , , 21 ij a i j i b
• Здесь — неизвестные; — коэффициенты при неизвестных, где — номер уравнения, — номер неизвестного; — свободные члены (правые части). n xxx, . . . , , 21 ij a i j i b
 • Система наз. неоднородной, если не все равны нулю. Система наз. однородной, если все равны нулю. i b
• Система наз. неоднородной, если не все равны нулю. Система наз. однородной, если все равны нулю. i b
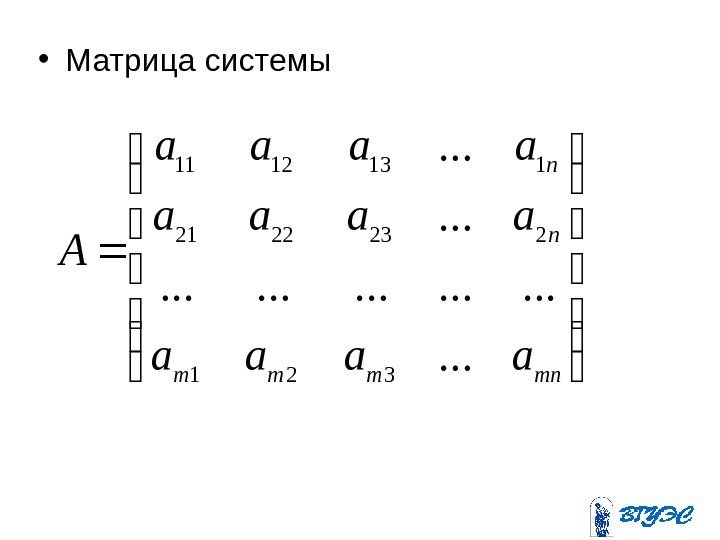
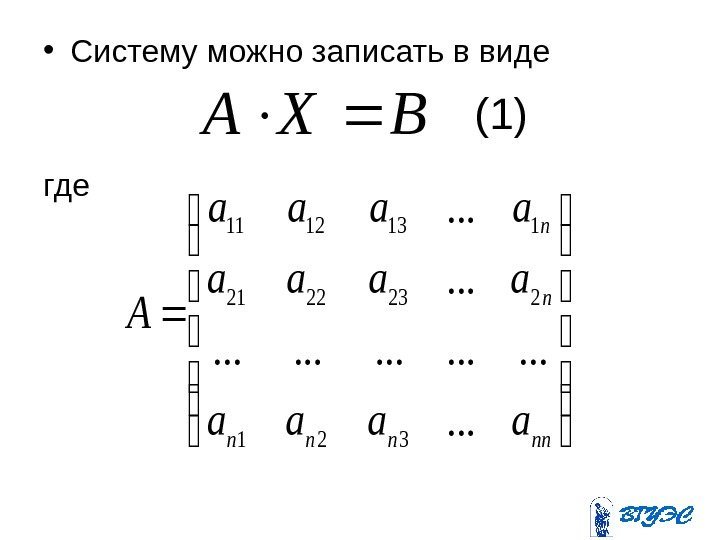
 • Матрица системы mnmmm n n aaaa A. . .
• Матрица системы mnmmm n n aaaa A. . .
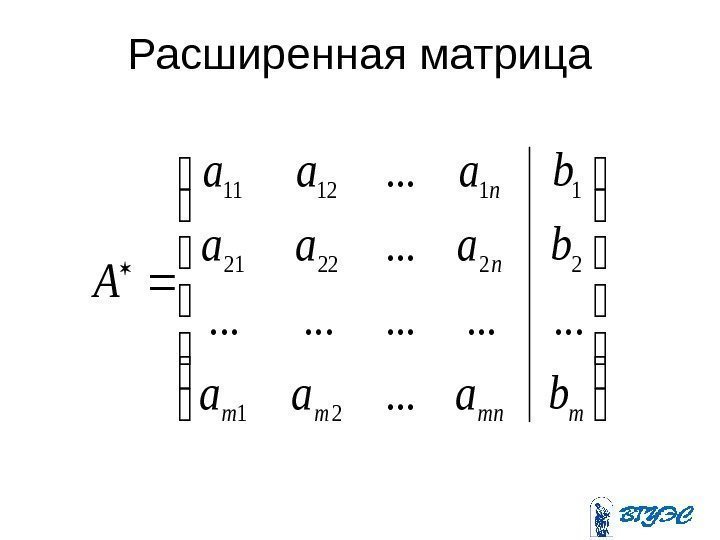
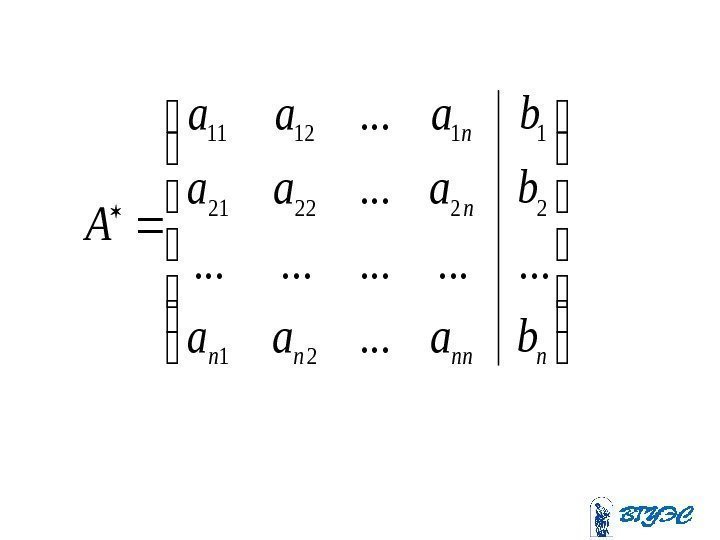
 Расширенная матрица mmnmm n n baaa A. . .
Расширенная матрица mmnmm n n baaa A. . .
 Решением системы будем называть упорядоченный набор чисел обращающий каждое уравнение системы в верное равенство. n xxx, . . . , ,
Решением системы будем называть упорядоченный набор чисел обращающий каждое уравнение системы в верное равенство. n xxx, . . . , ,
 Решить систему — значит найти все ее решения или доказать, что ни одного решения нет. Система, имеющая хотя бы одно решение, называется совместной. Если система имеет только одно решение, то она называется определенной.
Решить систему — значит найти все ее решения или доказать, что ни одного решения нет. Система, имеющая хотя бы одно решение, называется совместной. Если система имеет только одно решение, то она называется определенной.
 Если система не имеет решений, то она называется несовместной. Система, имеющая более чем одно решение, называется неопределенной (совместной и неопределенной). Если число уравнений системы совпадает с числом неизвестных , то система называется квадратной.
Если система не имеет решений, то она называется несовместной. Система, имеющая более чем одно решение, называется неопределенной (совместной и неопределенной). Если число уравнений системы совпадает с числом неизвестных , то система называется квадратной.
 Две системы, множества решений которых совпадают, называются эквивалентными или равносильными. Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием.
Две системы, множества решений которых совпадают, называются эквивалентными или равносильными. Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием.
 Метод Гаусса
Метод Гаусса
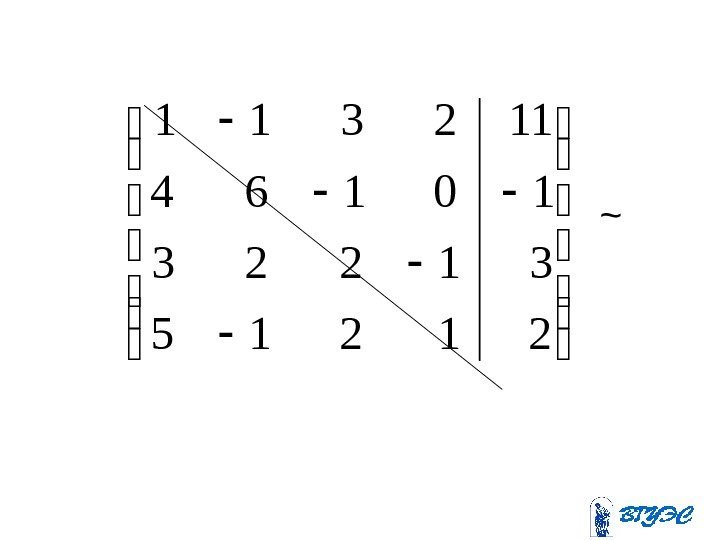
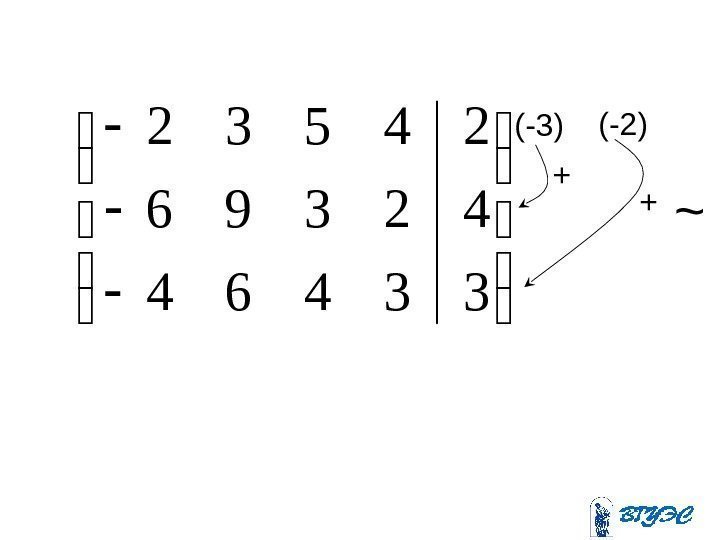
 Рассмотрим квадратную систему: . 225 ; 3223 ; 164 ; 1123 4321 321 4321 xxxx
Рассмотрим квадратную систему: . 225 ; 3223 ; 164 ; 1123 4321 321 4321 xxxx
 ~
~
 ~
~
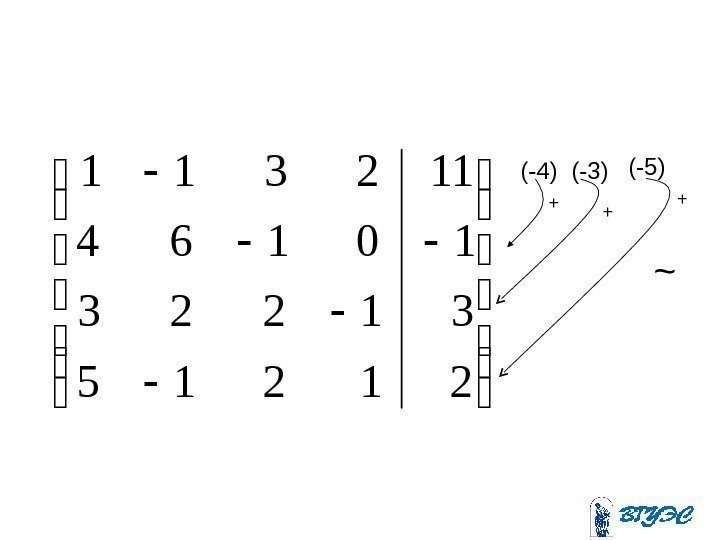
 ~ 21215 31223 10164 112311(-4) (-3) (-5) + + +
~ 21215 31223 10164 112311(-4) (-3) (-5) + + +
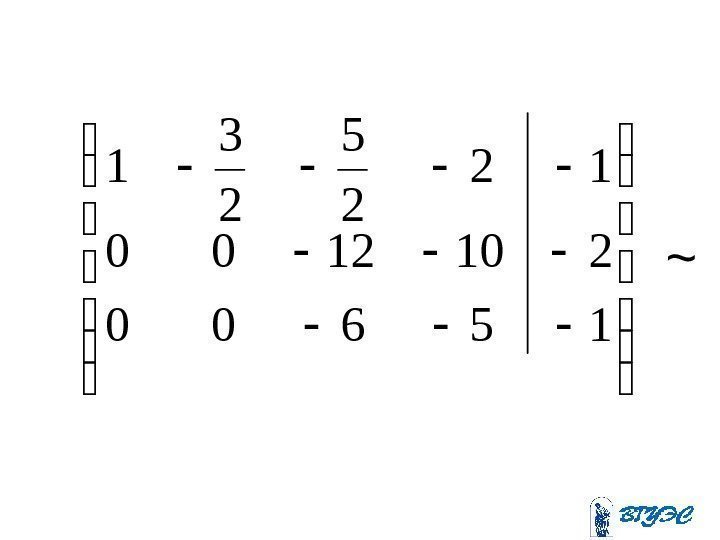
 5391340 307750 45813100 112311(-2) (-5) 2 + +
5391340 307750 45813100 112311(-2) (-5) 2 + +
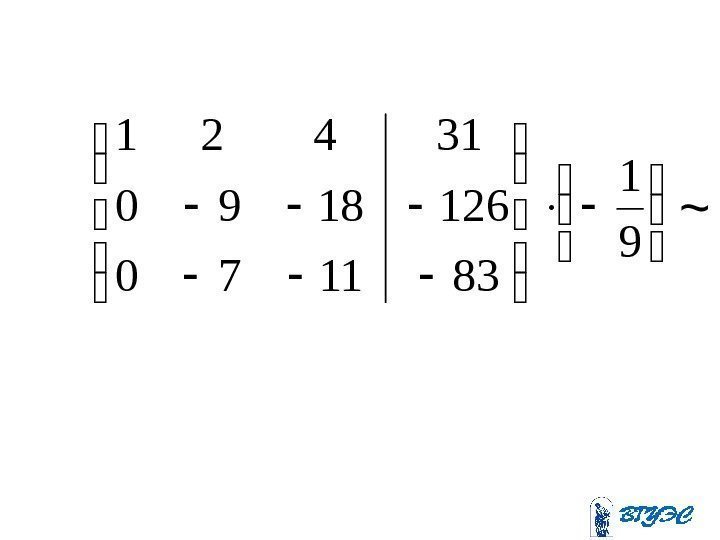
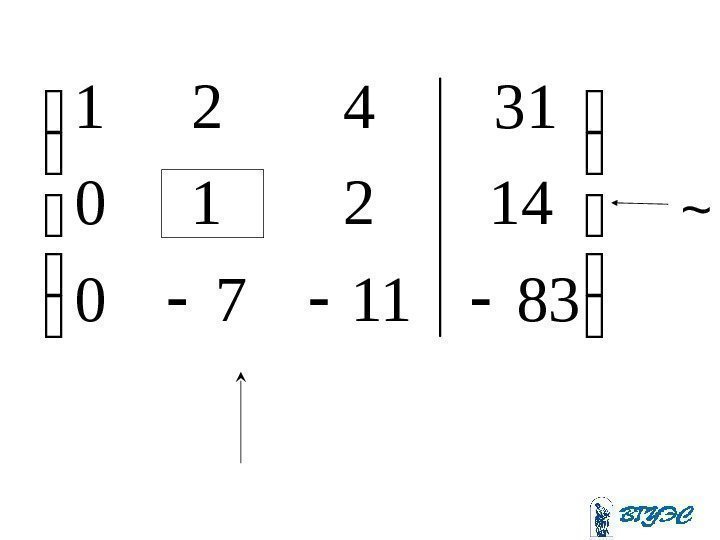
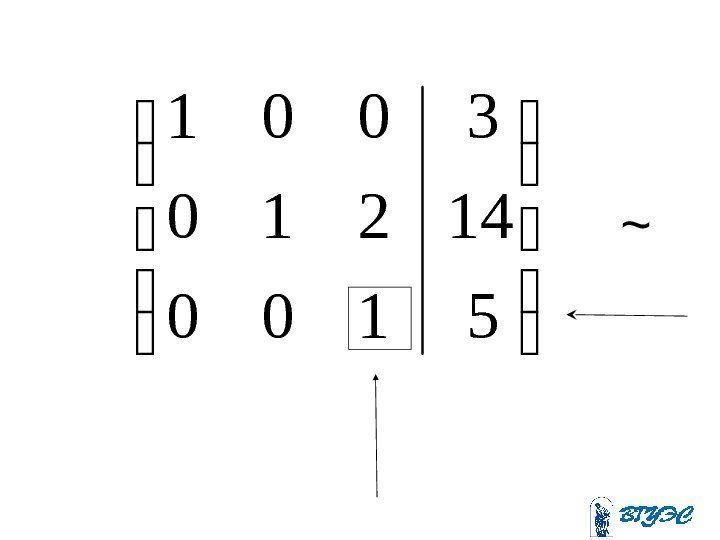
 175293900 156100 45813100 112311(-39) + ~
175293900 156100 45813100 112311(-39) + ~

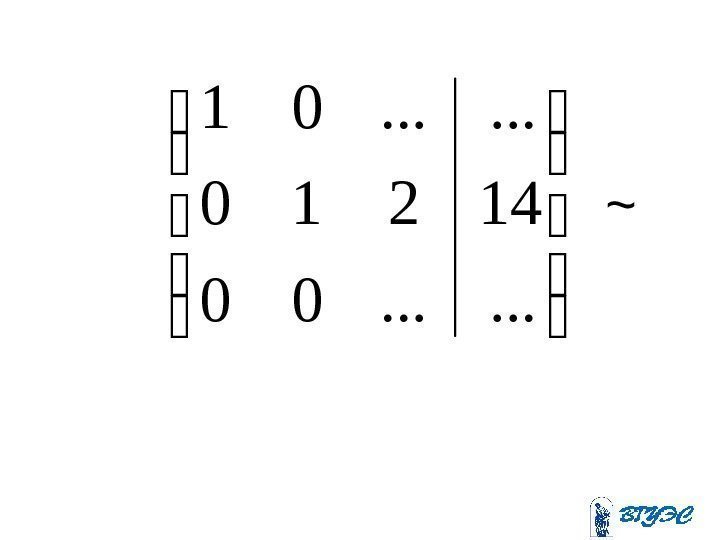
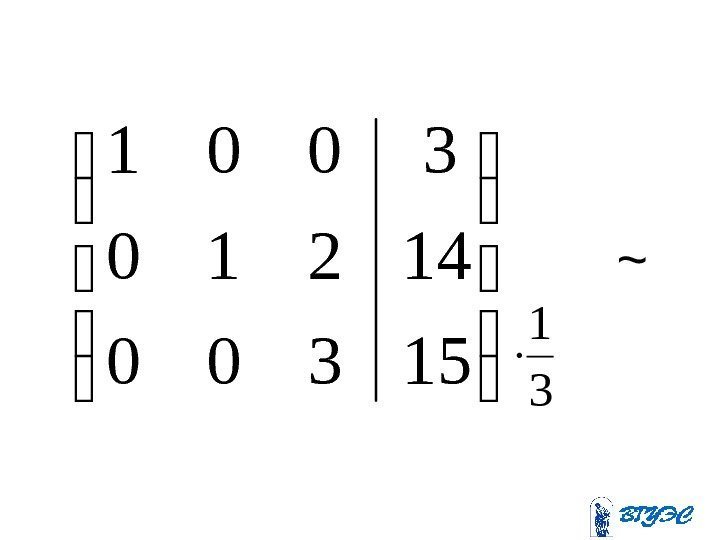
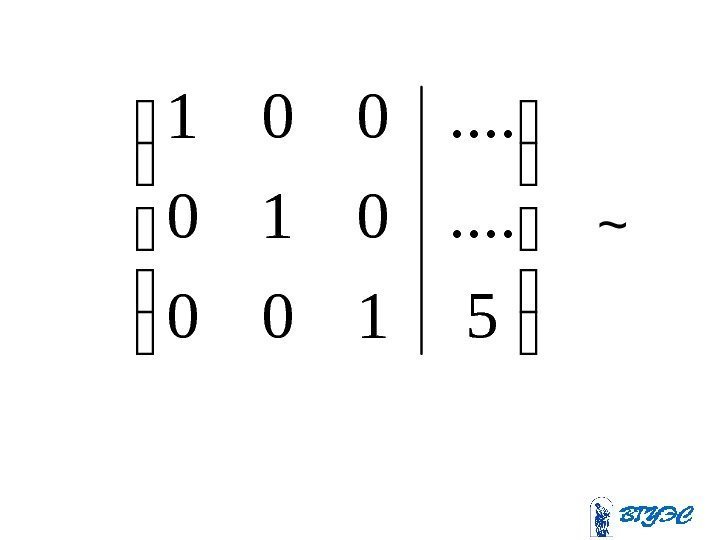
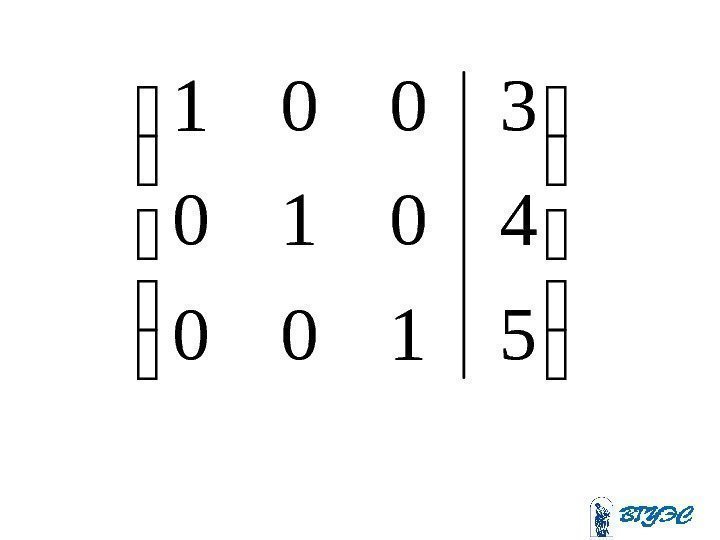
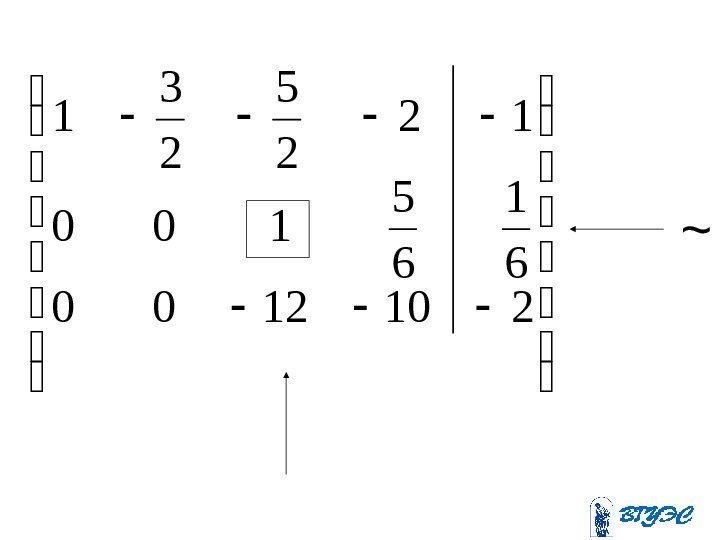
 Полученная матрица соответствует системе: . 410205 ; 15 6 ; 45 81310 ; 11 23 443 4321 x xx xxxx
Полученная матрица соответствует системе: . 410205 ; 15 6 ; 45 81310 ; 11 23 443 4321 x xx xxxx
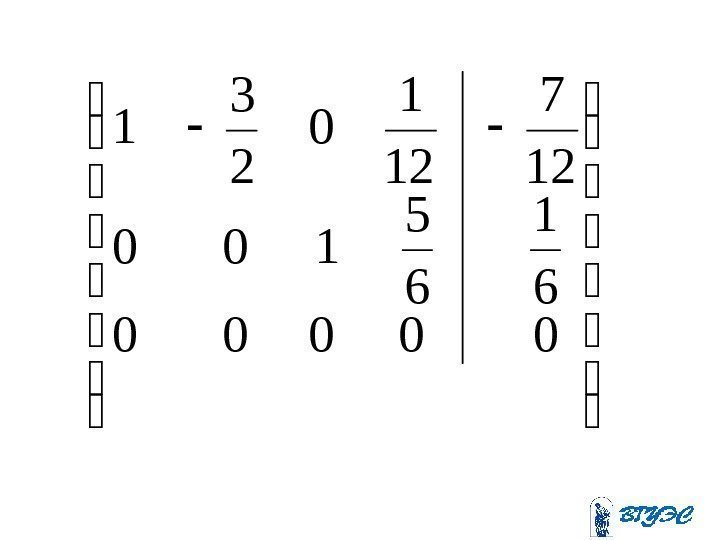
 . 2 ; 312152615615 ; 10163945 2831345 8134510 ; 149111 2233111 2311 4 43 2 4321 x xx х xxxx
. 2 ; 312152615615 ; 10163945 2831345 8134510 ; 149111 2233111 2311 4 43 2 4321 x xx х xxxx
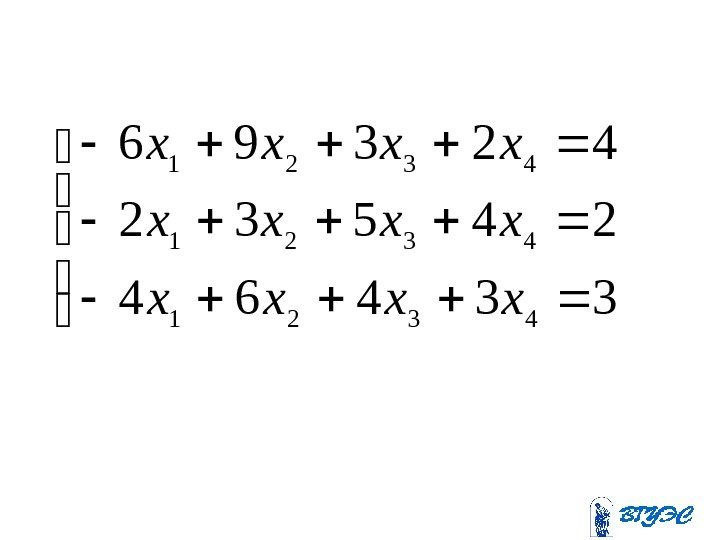 33464 24532 42396 4321 xxxx
33464 24532 42396 4321 xxxx
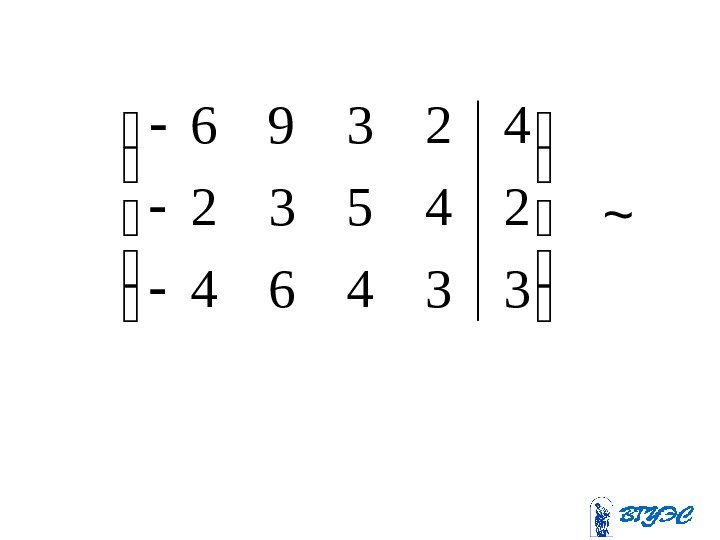
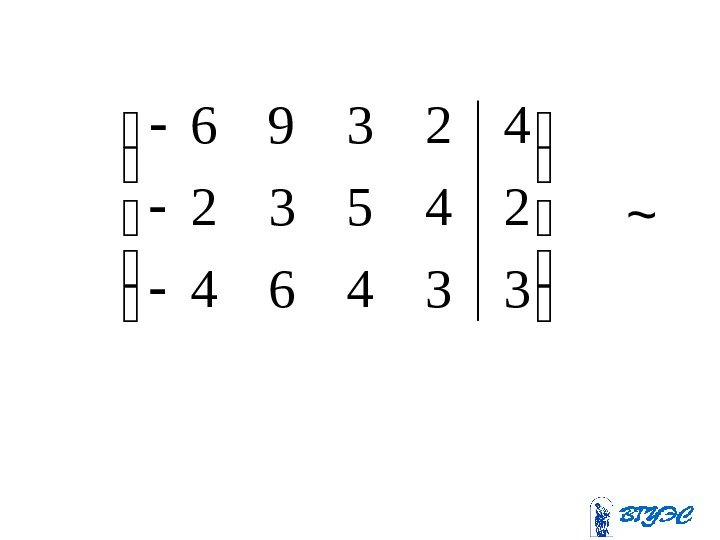
 33464 24532 42396~
33464 24532 42396~
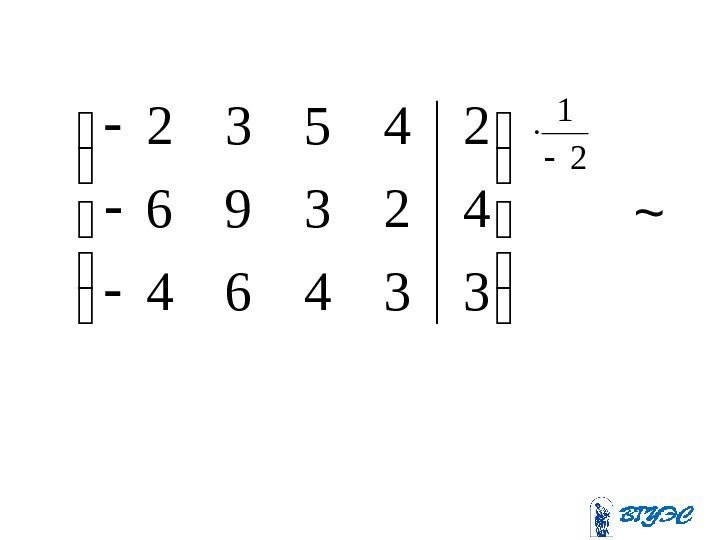
 33464 42396 24532(-3) (-2) + + ~
33464 42396 24532(-3) (-2) + + ~
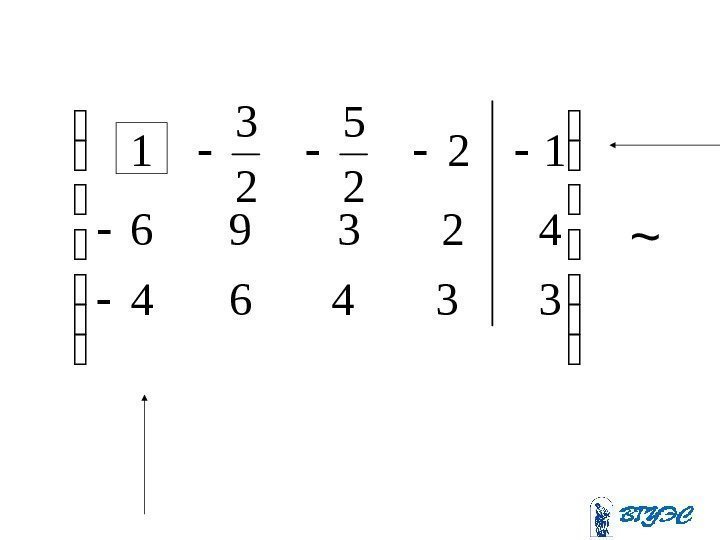
 15600 2101200 24532~
15600 2101200 24532~
 2101200 15600 24532(-2) + ~
2101200 15600 24532(-2) + ~
 00000 15600 24532~
00000 15600 24532~

 • Рассмотрим минор назовем его базисным. Тогда базисные переменные. 012 60 52 31 , xx
• Рассмотрим минор назовем его базисным. Тогда базисные переменные. 012 60 52 31 , xx
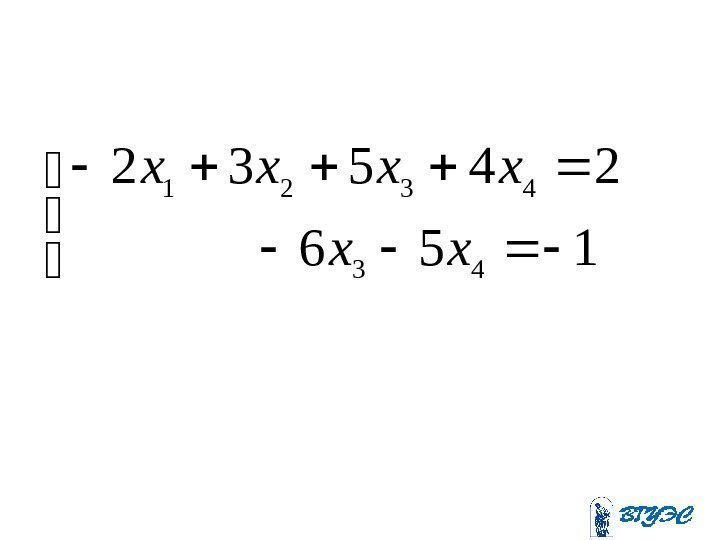 156 24532 43 4321 xx xxxx
156 24532 43 4321 xx xxxx
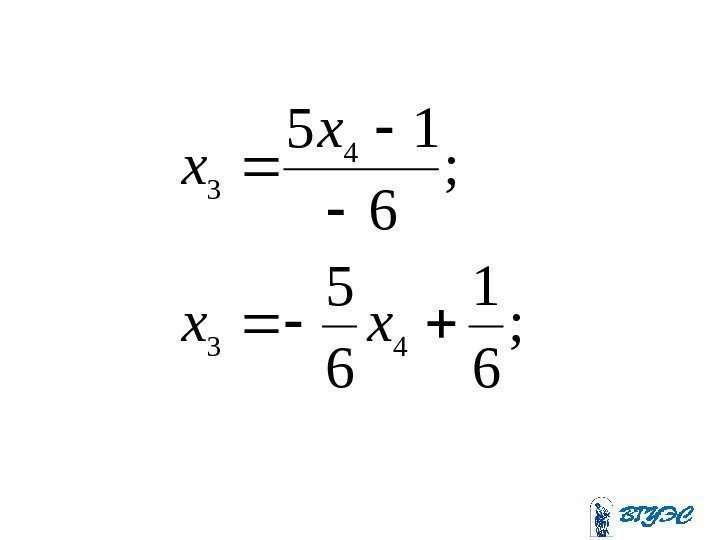 ; 61 65 ; 6 15 43 4 3 xx x x
; 61 65 ; 6 15 43 4 3 xx x x
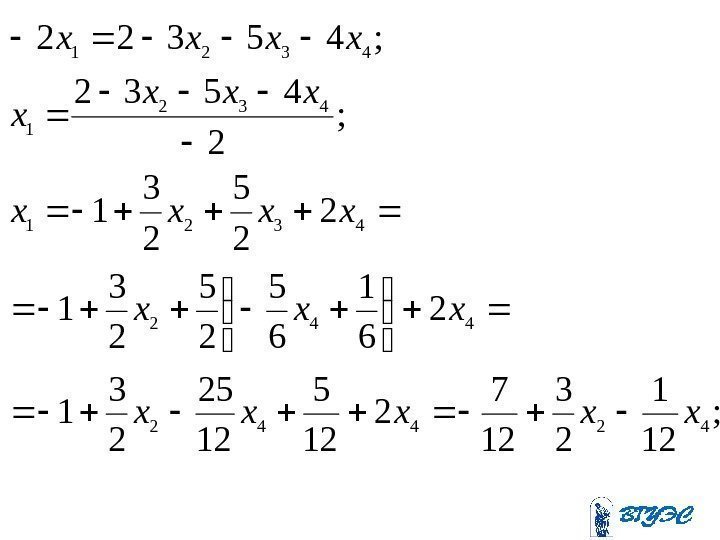 ; 12 1 23 12 7 2 12 5 12 25 23 1 2 61 65 25 23 1 2 25 23 1 ; 2 4532 ; 45322 42442 4321 4321 xxxxx xxxx
; 12 1 23 12 7 2 12 5 12 25 23 1 2 61 65 25 23 1 2 25 23 1 ; 2 4532 ; 45322 42442 4321 4321 xxxxx xxxx
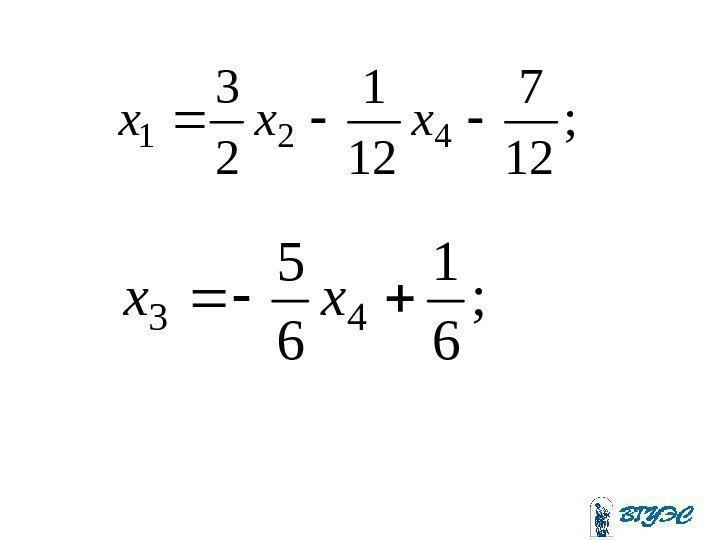 ; 12 7 12 1 2 3 421 xxx ; 6 1 6 5 43 xx
; 12 7 12 1 2 3 421 xxx ; 6 1 6 5 43 xx
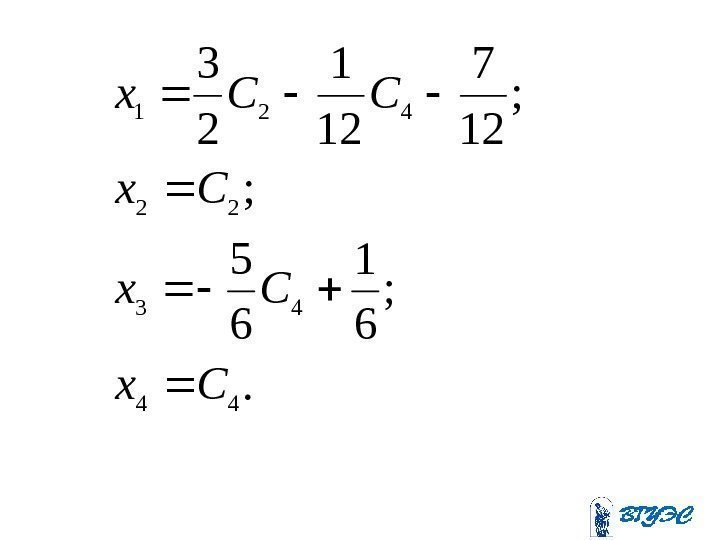 . ; 6 1 6 5 ; ; 12 7 12 1 2 3 44 43 22 421 Cx Cx Cx CCx
. ; 6 1 6 5 ; ; 12 7 12 1 2 3 44 43 22 421 Cx Cx Cx CCx
 Метод Жордана-Гаусса
Метод Жордана-Гаусса
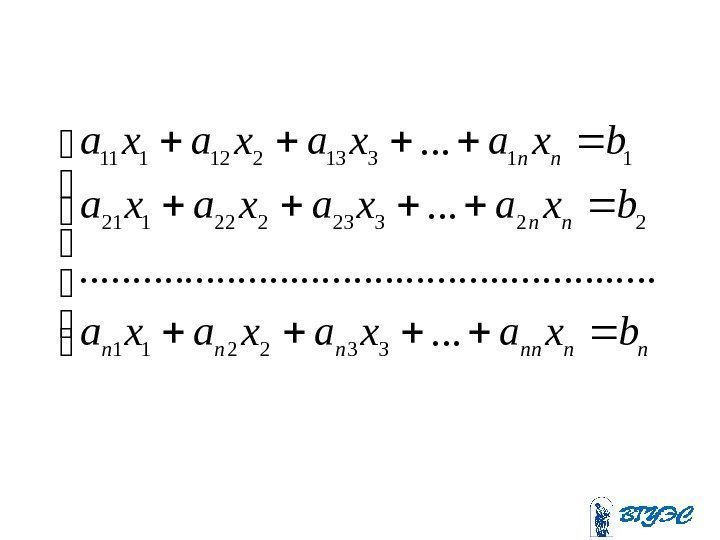 nnnnnnn nn nn bxa. . . xaxaxa. . . . bxa. . . xaxaxa
nnnnnnn nn nn bxa. . . xaxaxa. . . . bxa. . . xaxaxa
 nnnnn n n baaa A. . .
nnnnn n n baaa A. . .
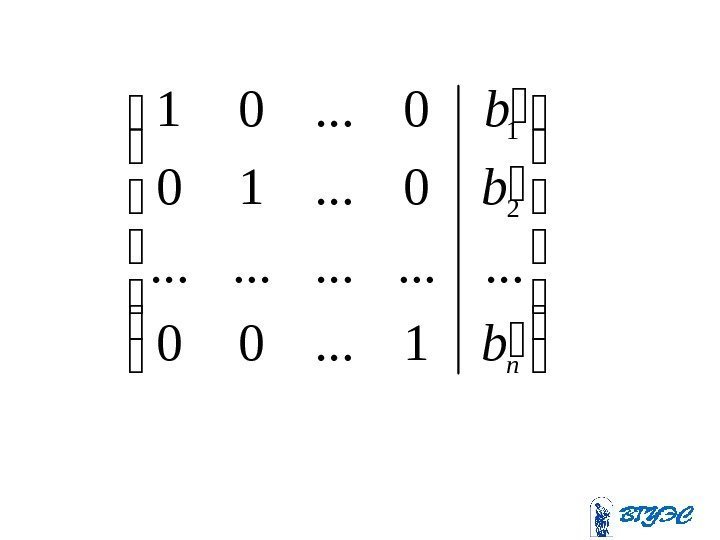
 n b b b 1. . . 00. . . . 0. . . 10 0. . .
n b b b 1. . . 00. . . . 0. . . 10 0. . .
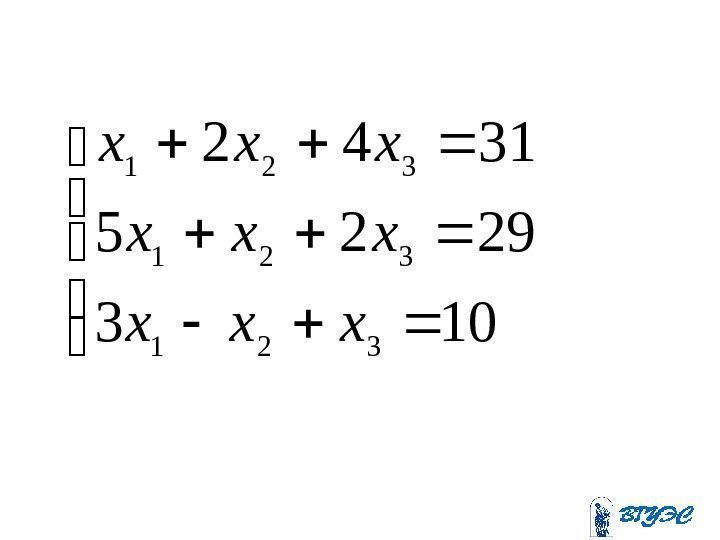 103 2925 3142 321 321 xxx xxx
103 2925 3142 321 321 xxx xxx

 a cb d
a cb d
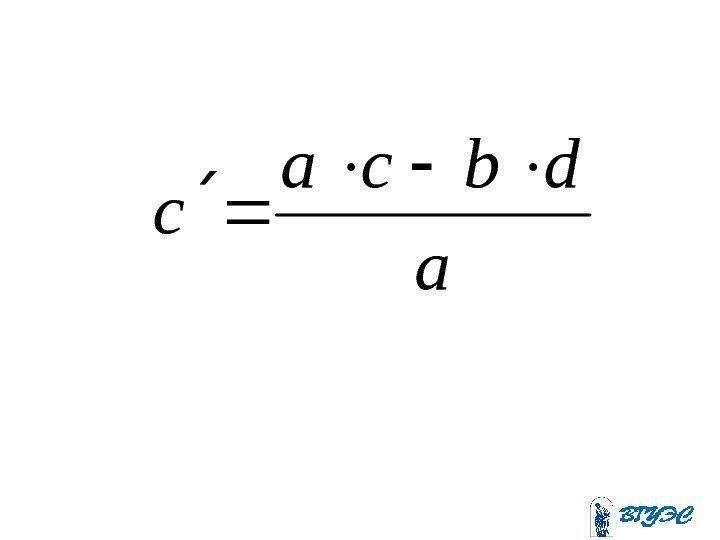 a dbсa с
a dbсa с
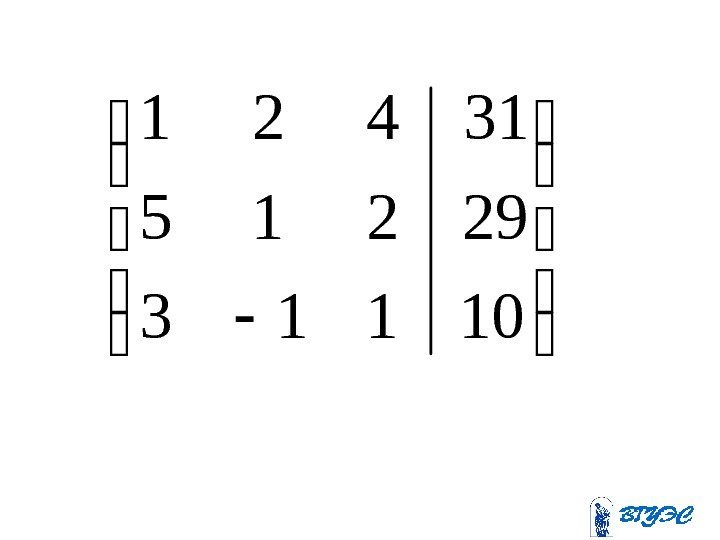
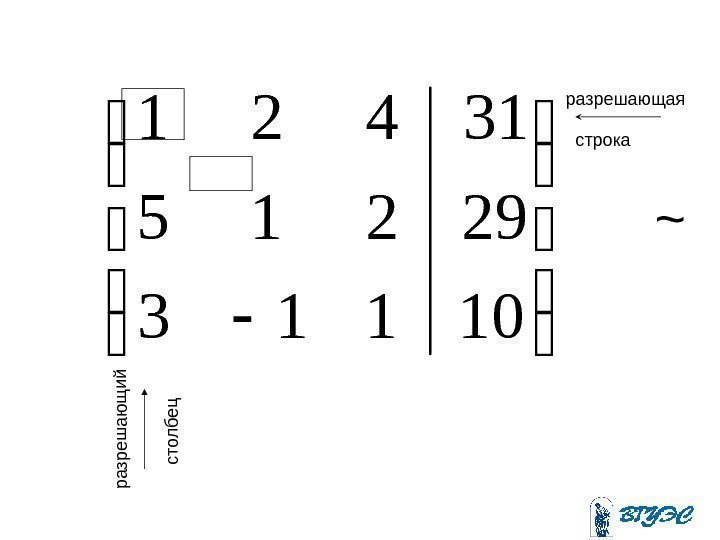
 10113 29215 31421 разрешающаяразреш аю щ ий строка стол б ец ~
10113 29215 31421 разрешающаяразреш аю щ ий строка стол б ец ~
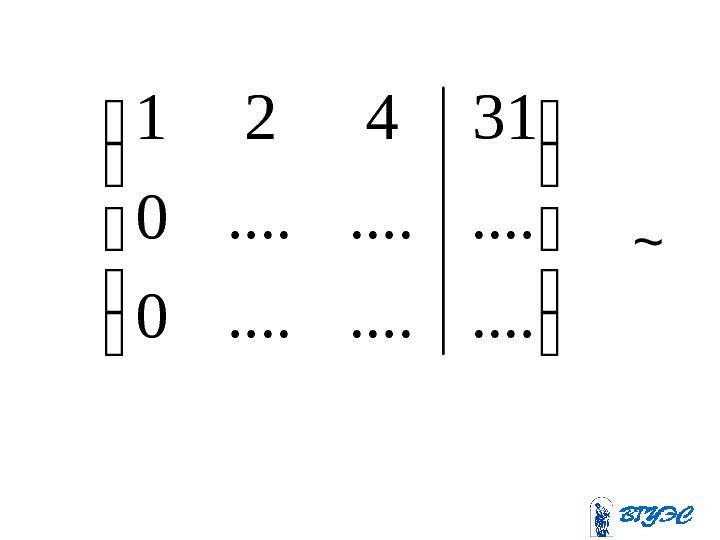
 . . . 0 31421~
. . . 0 31421~
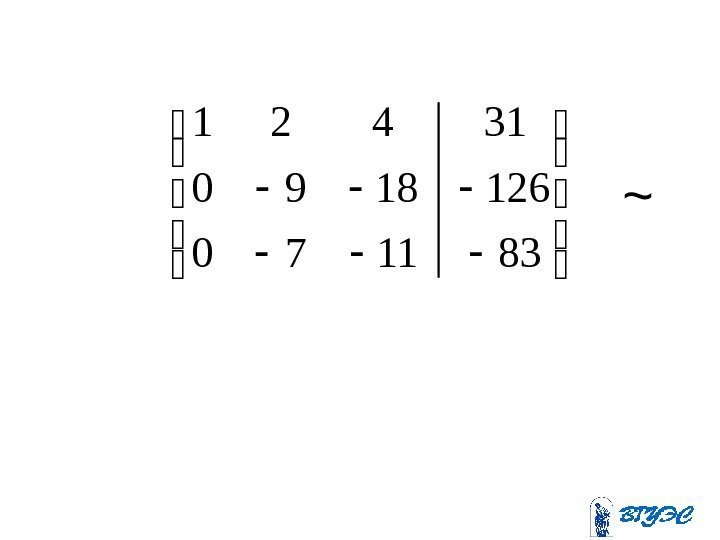
 831170 1261890 31421~
831170 1261890 31421~
 9 1 831170 1261890 31421~
9 1 831170 1261890 31421~
 831170 14210 31421~
831170 14210 31421~
 . . . 00 14210. . . 01~
. . . 00 14210. . . 01~
 15300 14210 3001 3 1 ~
15300 14210 3001 3 1 ~
 5100 14210 3001~
5100 14210 3001~
 5100. . 010. . 001~
5100. . 010. . 001~

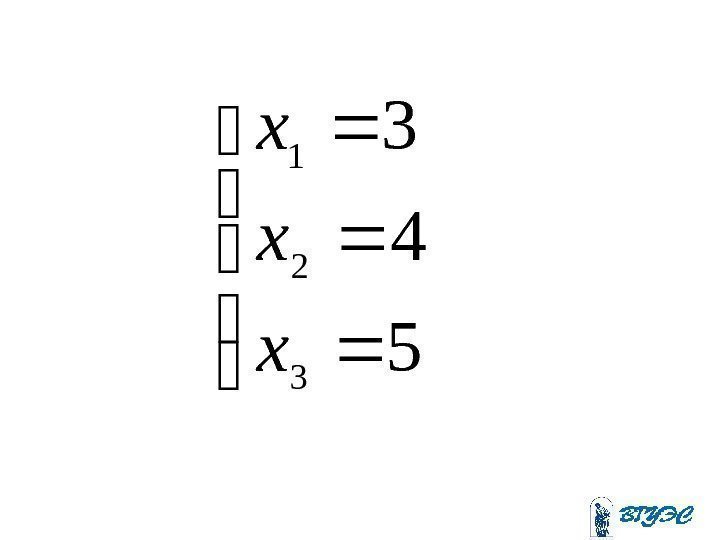 5 4 3 3 2 1 x x x
5 4 3 3 2 1 x x x
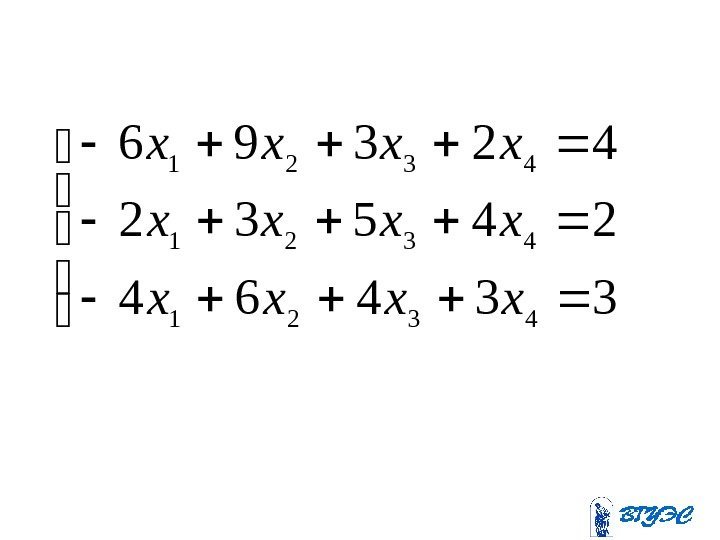 33464 24532 42396 4321 xxxx
33464 24532 42396 4321 xxxx
 33464 24532 42396~
33464 24532 42396~
 33464 42396 24532 2 1 ~
33464 42396 24532 2 1 ~
 3 3 4 6 4 4 2 3 9 6 12 2 5 2 3 1 ~
3 3 4 6 4 4 2 3 9 6 12 2 5 2 3 1 ~
 1560 0 210120 0 12 2 5 2 3 1~
1560 0 210120 0 12 2 5 2 3 1~
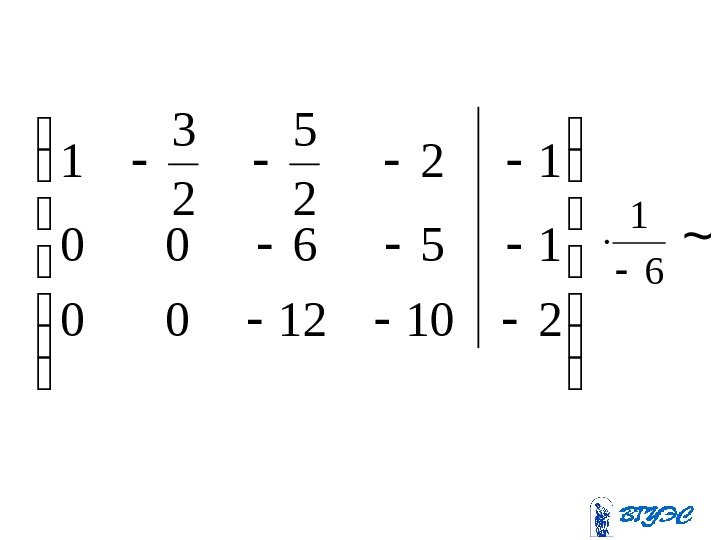 210120 0 1560 0 12 2 5 2 3 1 6 1 ~
210120 0 1560 0 12 2 5 2 3 1 6 1 ~
 210120 0 6 1 6 5 1 0 0 12 2 5 2 3 1~
210120 0 6 1 6 5 1 0 0 12 2 5 2 3 1~

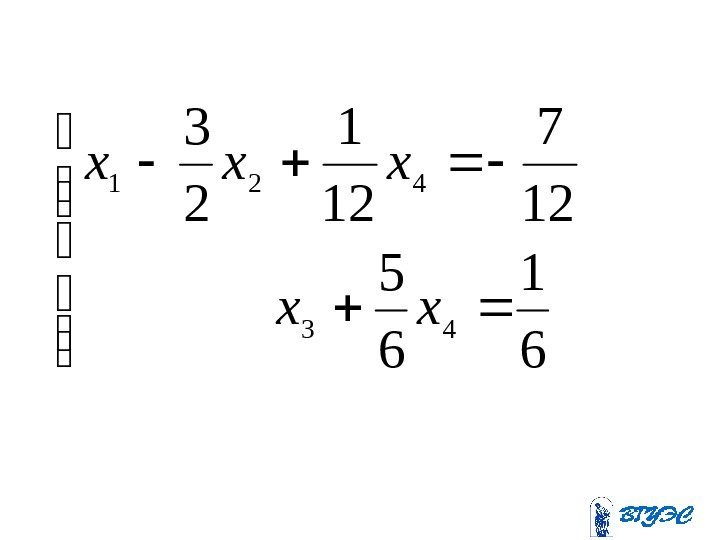 6 1 6 5 12 7 12 1 2 3 43 421 xx xxx
6 1 6 5 12 7 12 1 2 3 43 421 xx xxx
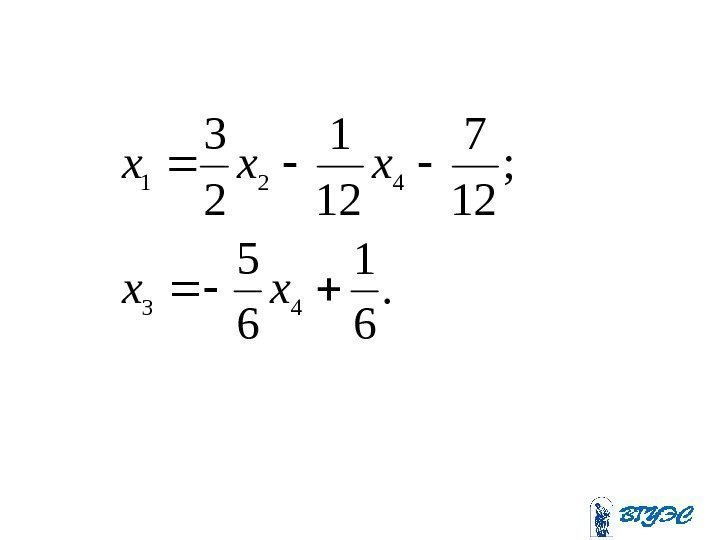 . 61 65 ; 12 7 12 1 2343 421 xx xxx
. 61 65 ; 12 7 12 1 2343 421 xx xxx
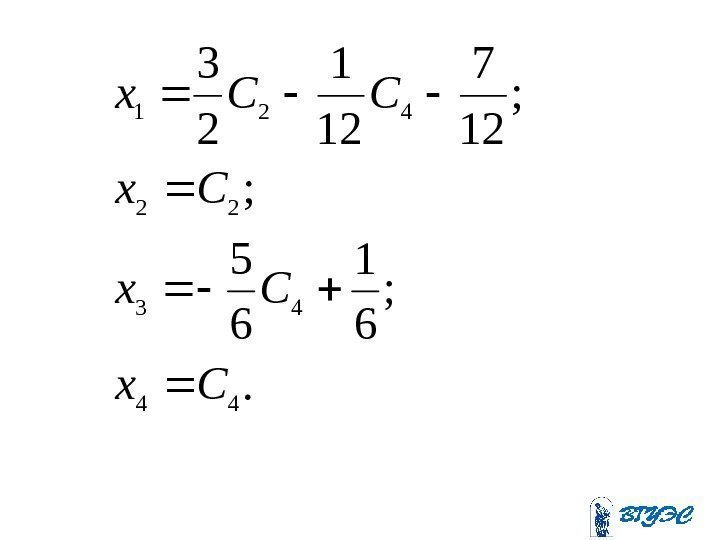 . ; 6 1 6 5 ; ; 12 7 12 1 2 3 44 43 22 421 Cx Cx Cx CCx
. ; 6 1 6 5 ; ; 12 7 12 1 2 3 44 43 22 421 Cx Cx Cx CCx
 Матричный метод
Матричный метод
 • С помощью этого метода можно решать квадратные системы линейных уравнений
• С помощью этого метода можно решать квадратные системы линейных уравнений
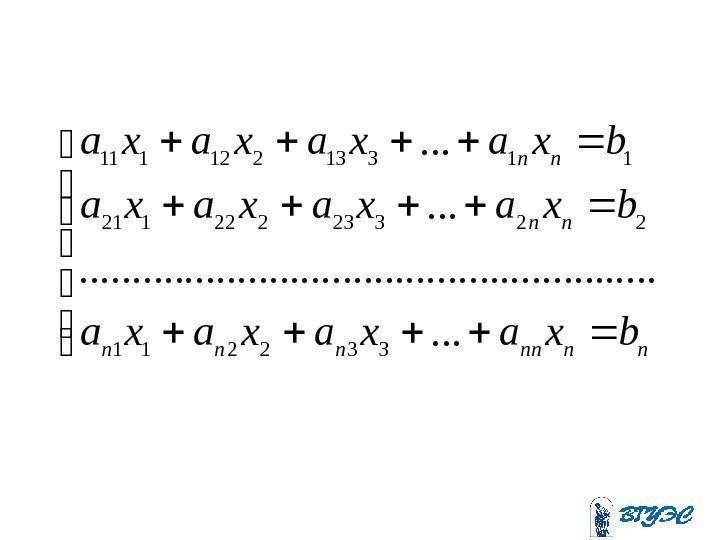 nnnnnnn nn nn bxa. . . xaxaxa. . . . bxa. . . xaxaxa
nnnnnnn nn nn bxa. . . xaxaxa. . . . bxa. . . xaxaxa
 • Систему можно записать в виде где. BXA nnnnn n n aaaa A. . . 321 2232221 1131211 (1)
• Систему можно записать в виде где. BXA nnnnn n n aaaa A. . . 321 2232221 1131211 (1)
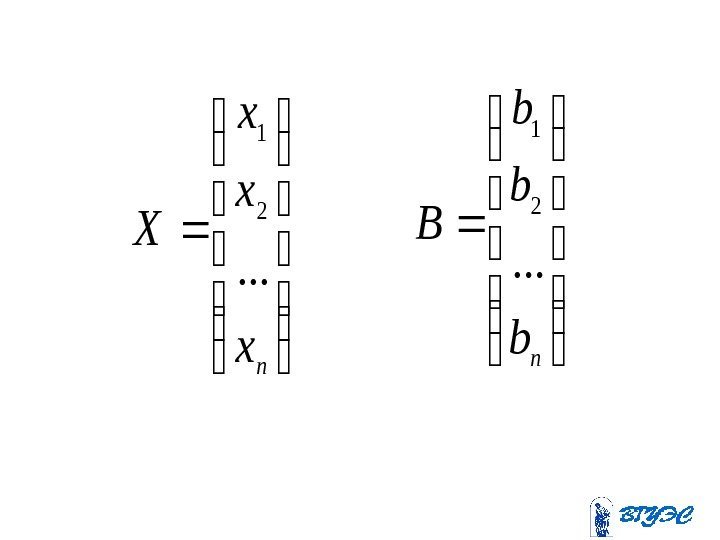
 n x x x X. . . 2 1 n b b b B. . .
n x x x X. . . 2 1 n b b b B. . .
 • Если матрица невырожденная, то можно выполнить преобразования. A BAXAA 11 BAX 1 (2)
• Если матрица невырожденная, то можно выполнить преобразования. A BAXAA 11 BAX 1 (2)
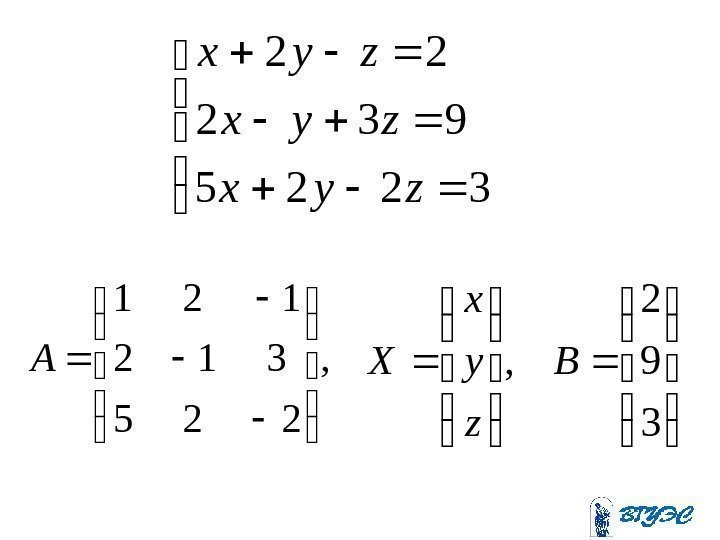 3225 932 22 zyx zyx , 225 312 121 A, z y x X
3225 932 22 zyx zyx , 225 312 121 A, z y x X
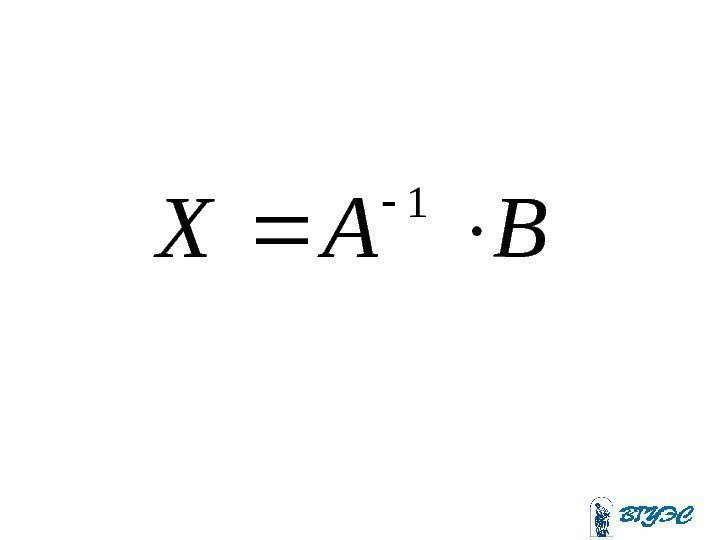 BAX
BAX
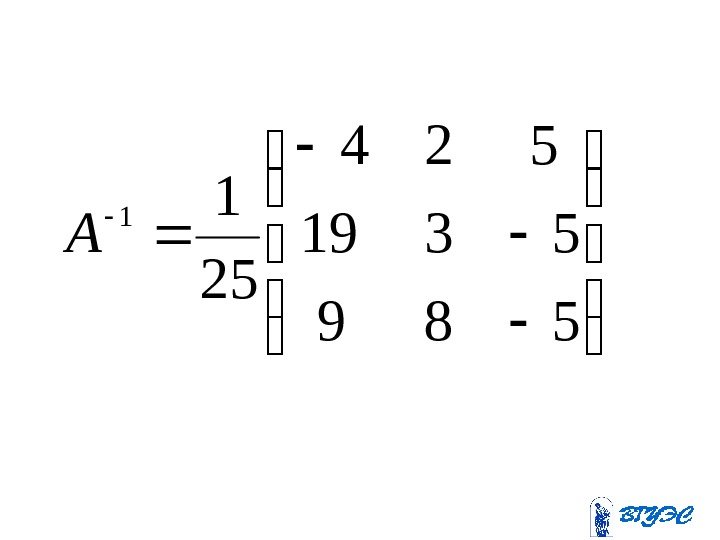
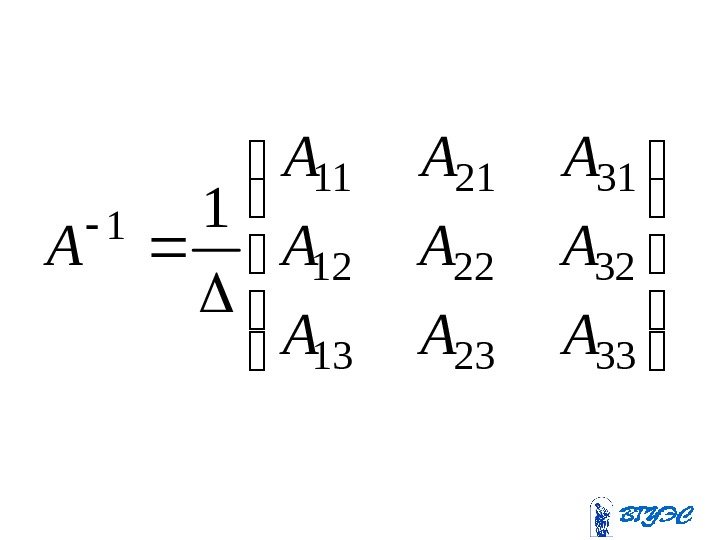 332313 322212 312111 1 1 ААА ААА А
332313 322212 312111 1 1 ААА ААА А
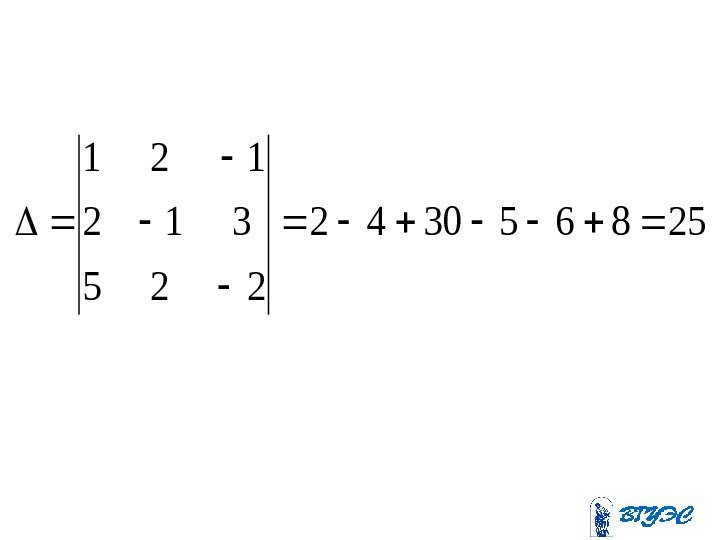
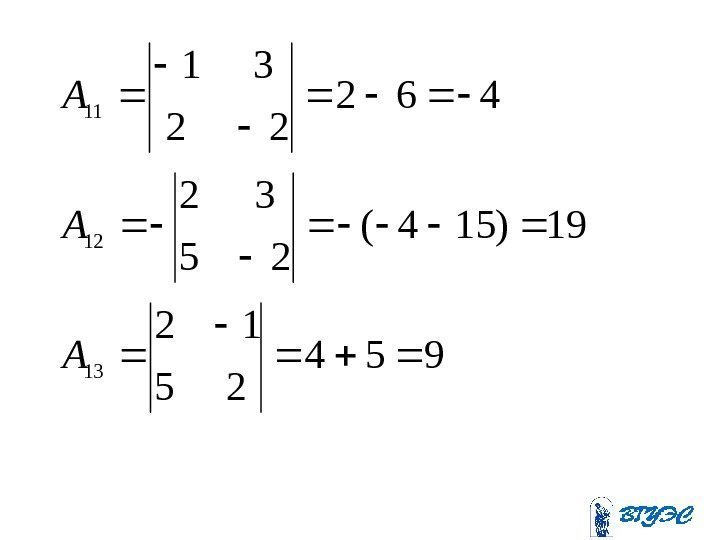 954 25 12 19)154(
954 25 12 19)154(
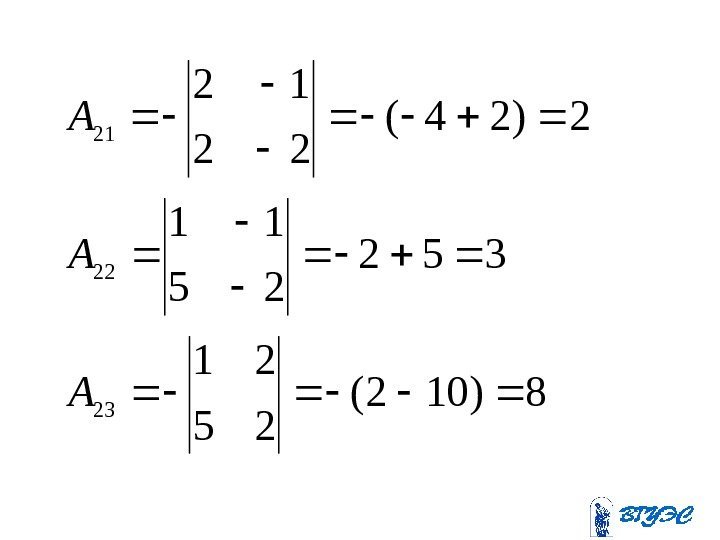 8)102( 25 21 352 25 11 2)24(
8)102( 25 21 352 25 11 2)24(
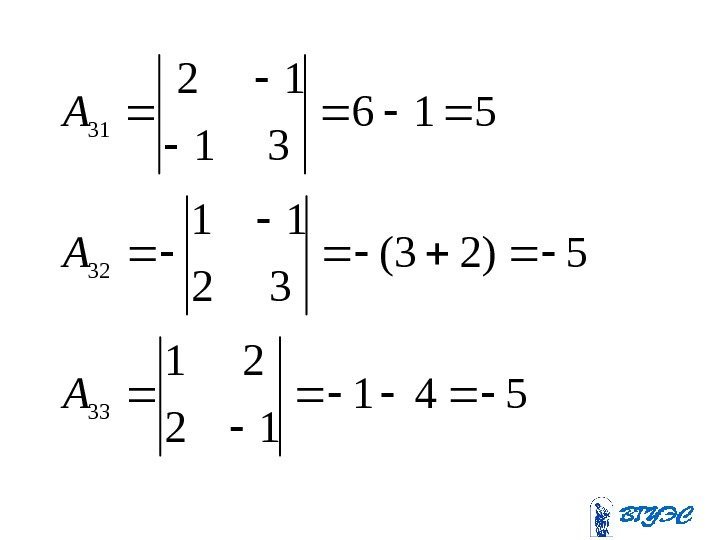 541 12 21 5)23(
541 12 21 5)23(

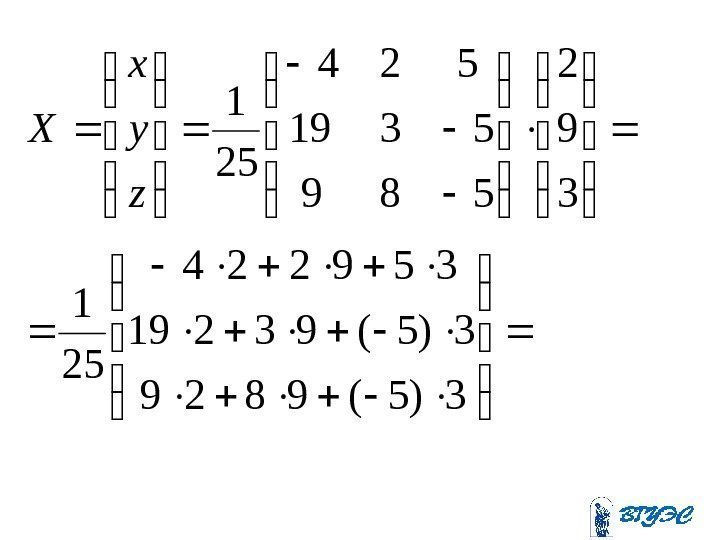 3)5(9829 3)5(93219 359224 25 1 3 9 2 589 5319 524 25 1 z y x X
3)5(9829 3)5(93219 359224 25 1 3 9 2 589 5319 524 25 1 z y x X
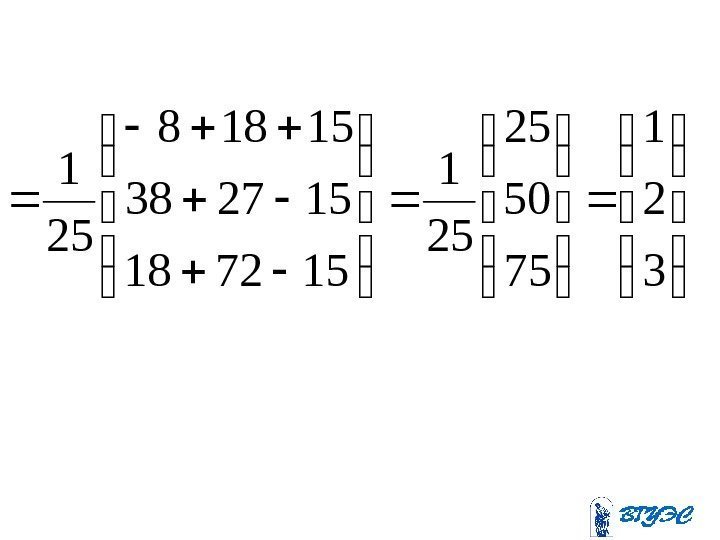
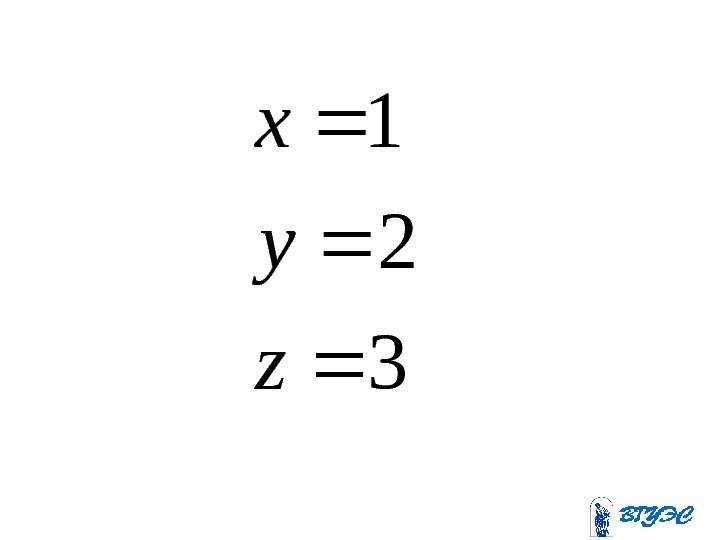 3 2 1 z y x
3 2 1 z y x
 Метод Крамера
Метод Крамера
 • Если определитель системы линейных уравнений с неизвестными отличен от нуля, то эта система является определенной и её единственное решение находится по формуламn n
• Если определитель системы линейных уравнений с неизвестными отличен от нуля, то эта система является определенной и её единственное решение находится по формуламn n
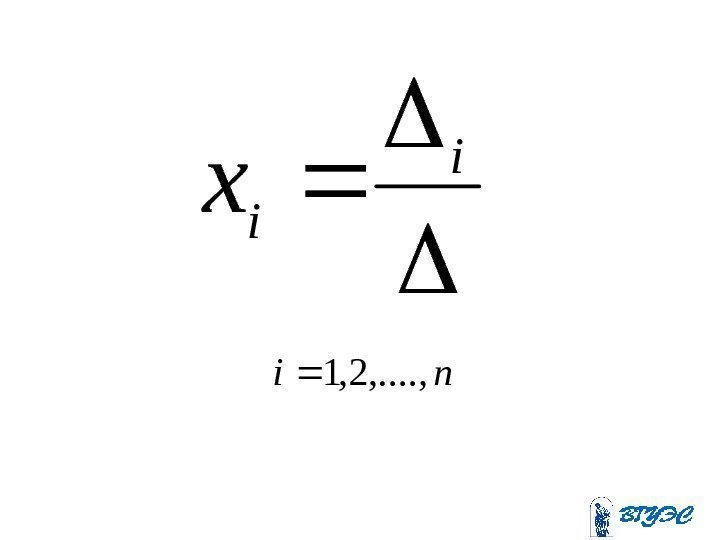 i ix ni, . . , 2,
i ix ni, . . , 2,
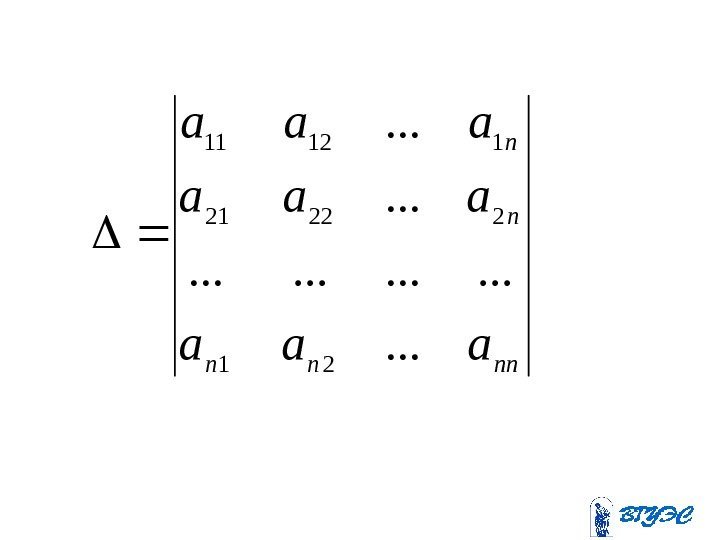
 nnnn n n aaa aaa. . . . .
nnnn n n aaa aaa. . . . .
 Здесь – – определитель, получающийся из определителя заменой ii -го-го столбца столбцом свободных членов. i
Здесь – – определитель, получающийся из определителя заменой ii -го-го столбца столбцом свободных членов. i
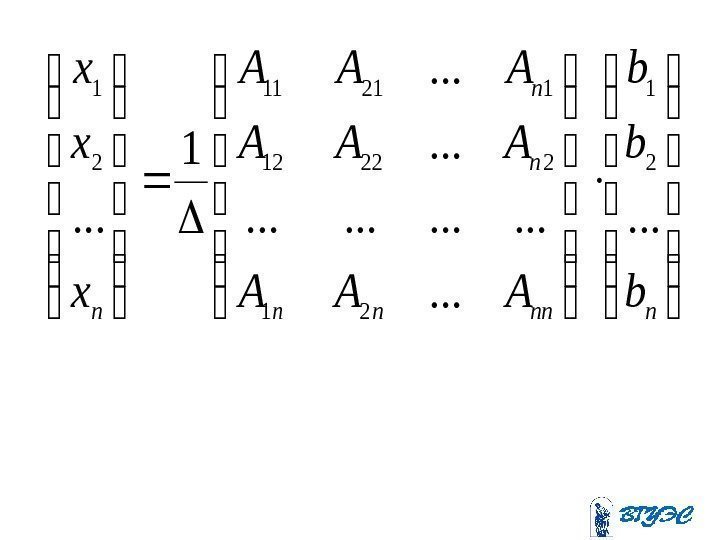
 nnnnn n b b b AAA AAA x x x. . . 1. . .
nnnnn n b b b AAA AAA x x x. . . 1. . .
 nn b. Ab. A x 1221111 1. . . nn nnnn n n b. Ab. A aab aab 1221111 2 2222 1121. . .
nn b. Ab. A x 1221111 1. . . nn nnnn n n b. Ab. A aab aab 1221111 2 2222 1121. . .
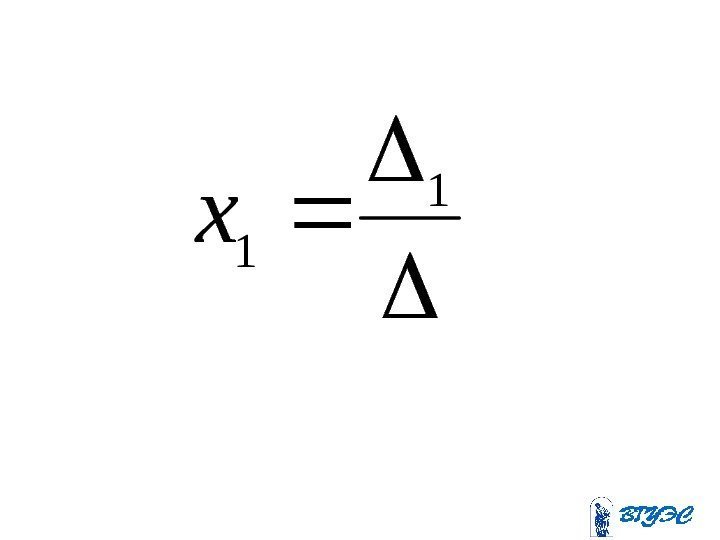 1 1 x
1 1 x
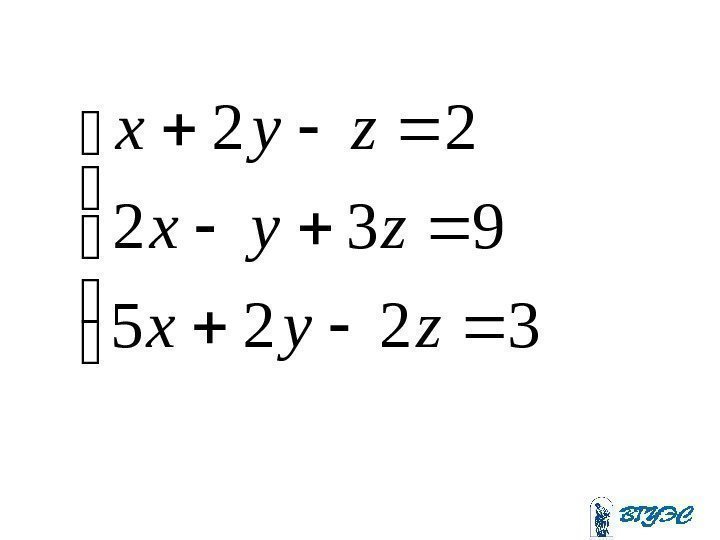 3225 932 22 zyx zyx
3225 932 22 zyx zyx
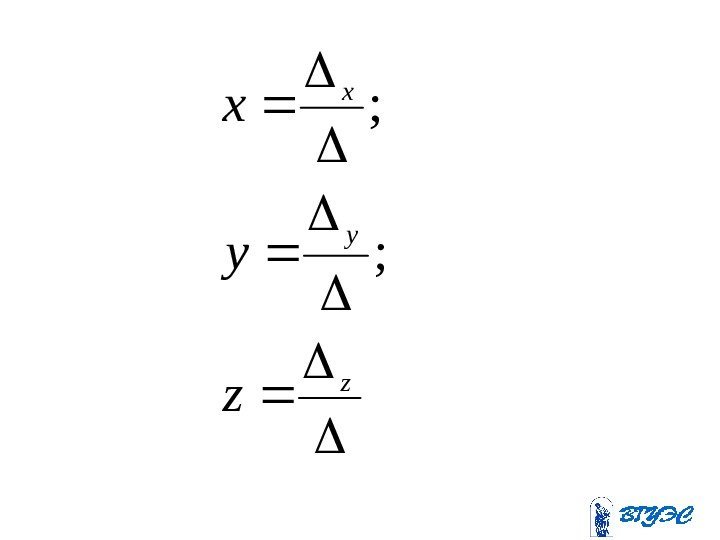 z y x ; ;
z y x ; ;
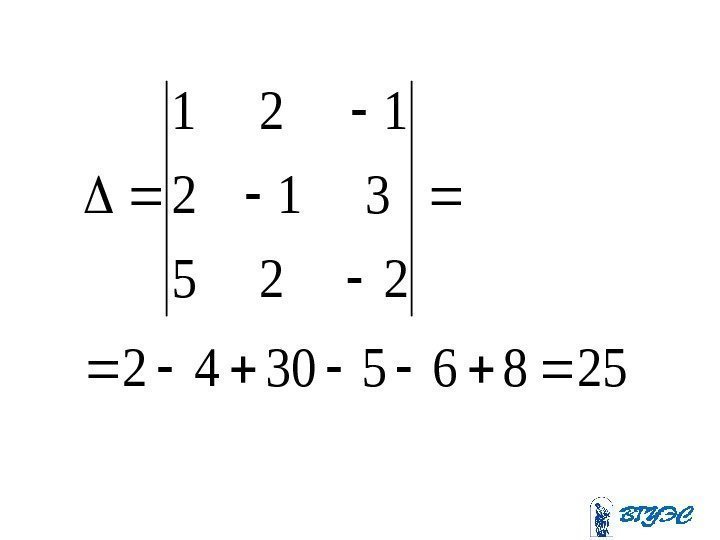
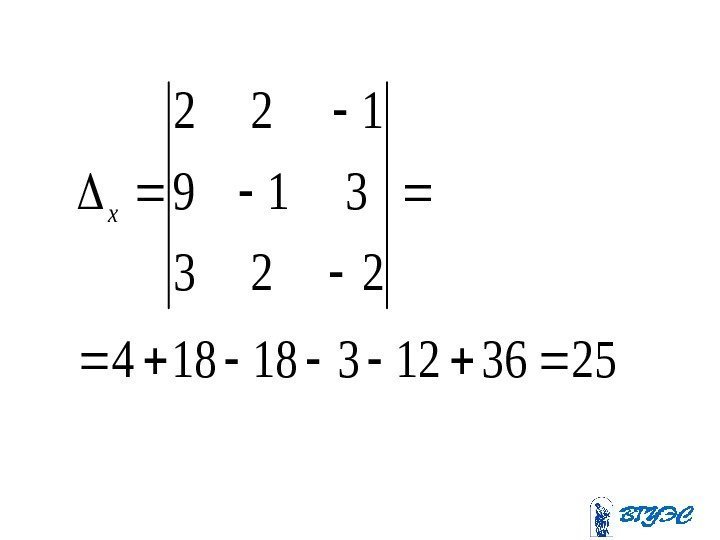 253612318184 223 319 122 x
253612318184 223 319 122 x
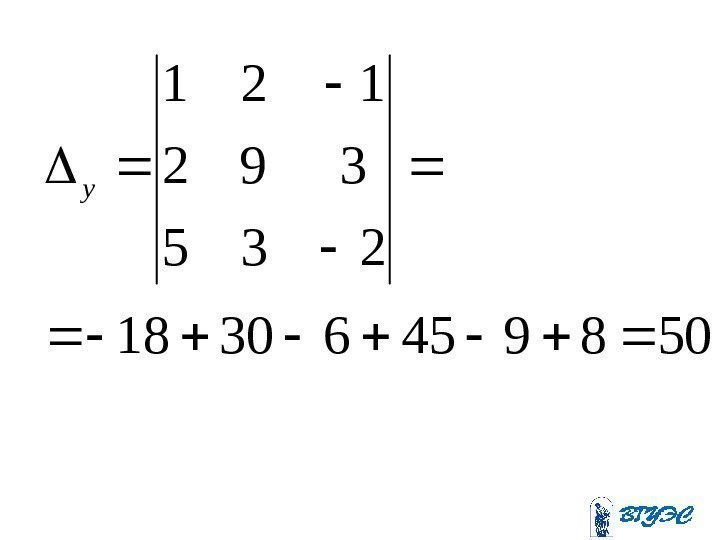 50894563018 235 392 121 y
50894563018 235 392 121 y
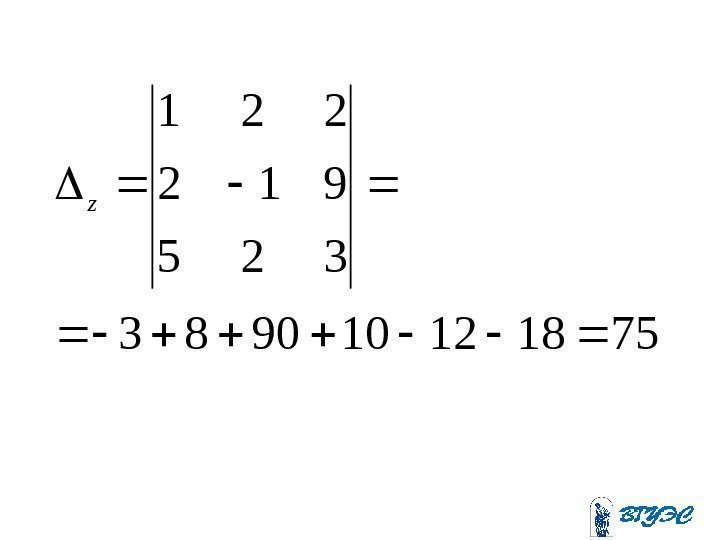 751812109083 325 912 221 z
751812109083 325 912 221 z
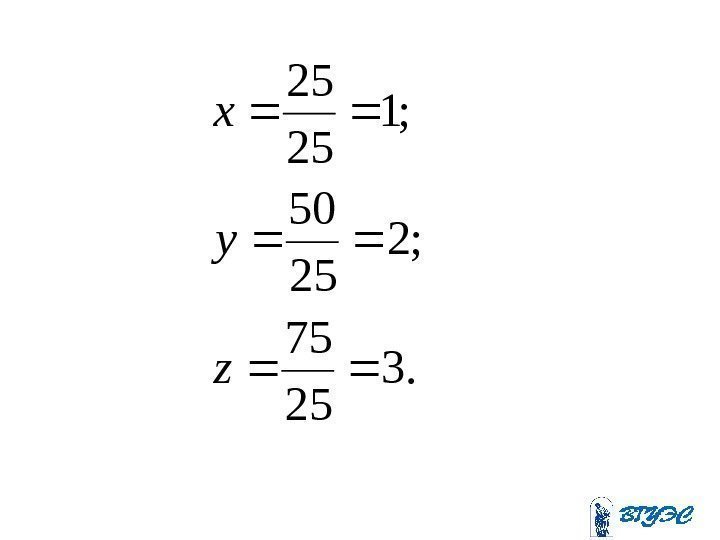 . 3 25 75 ; 2 25 50 ; 1 25 25 z y x
. 3 25 75 ; 2 25 50 ; 1 25 25 z y x
 • Если и по крайне мере один из определителей , то система не имеет решения. • Если , система либо не имеет решения, либо имеет бесконечно много решений. 00 i 00 i
• Если и по крайне мере один из определителей , то система не имеет решения. • Если , система либо не имеет решения, либо имеет бесконечно много решений. 00 i 00 i
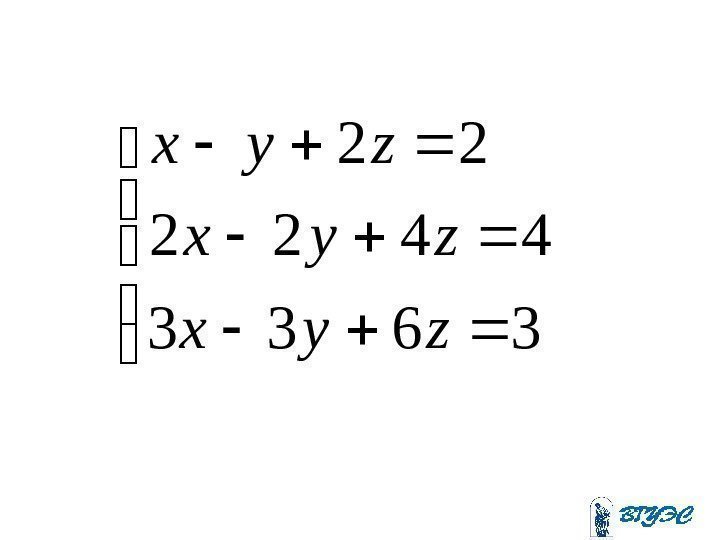 3633 4422 22 zyx zyx
3633 4422 22 zyx zyx
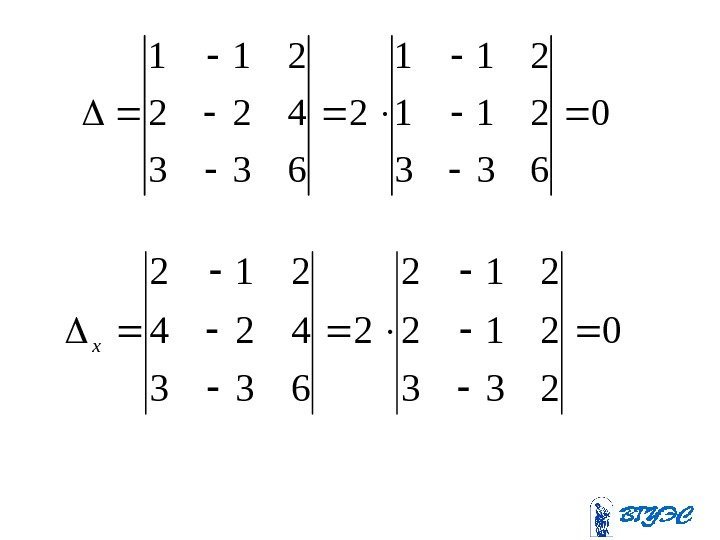 0 633 211 2 633 422 211 0 233 212 2 633 424 212 x
0 633 211 2 633 422 211 0 233 212 2 633 424 212 x
 0 633 221 2 633 442 221 y 0 333 211 2 333 422 211 z
0 633 221 2 633 442 221 y 0 333 211 2 333 422 211 z
 • Система не имеет решения, т. к. первое и третье уравнения противоречивы
• Система не имеет решения, т. к. первое и третье уравнения противоречивы
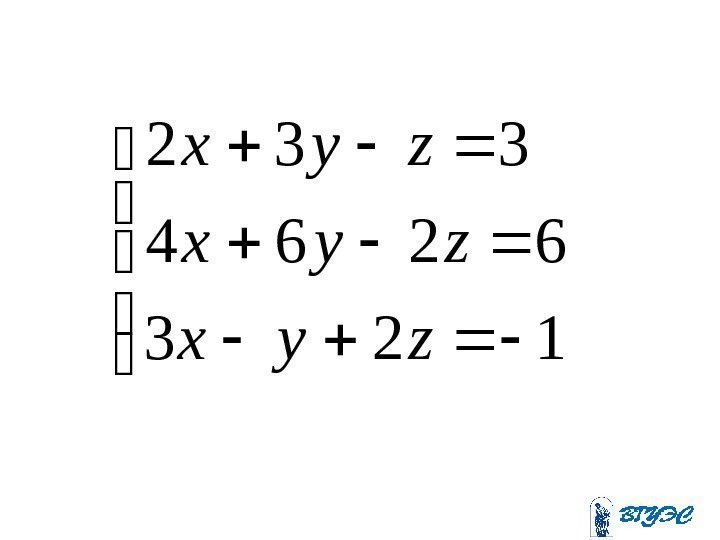 123 6264 332 zyx zyx
123 6264 332 zyx zyx
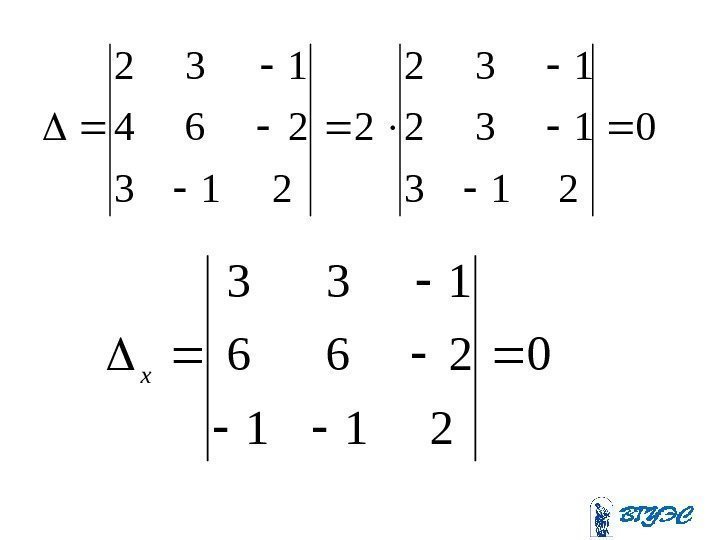 0 213 132 2 213 264 132 0 211 266 133 x
0 213 132 2 213 264 132 0 211 266 133 x
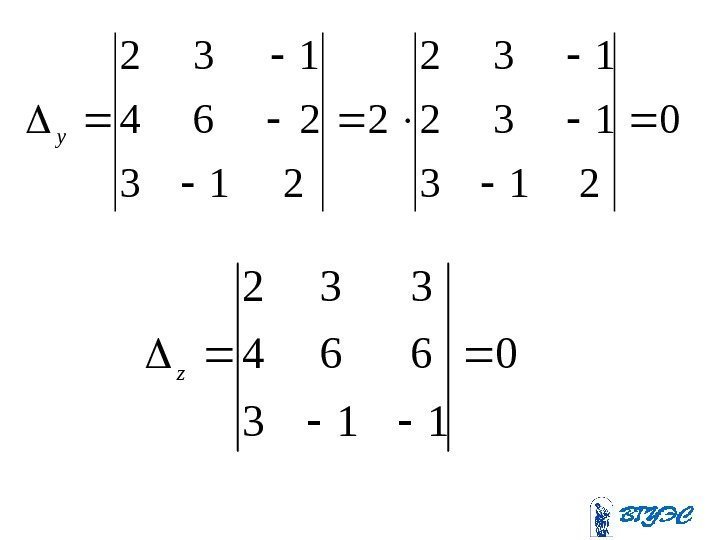 0 213 132 2 213 264 132 y 0 113 664 332 z
0 213 132 2 213 264 132 y 0 113 664 332 z
 • Второе уравнение получается умножением первого на два. Данная система равносильна системе Система имеет бесчисленное множество решений. 123 332 zyx
• Второе уравнение получается умножением первого на два. Данная система равносильна системе Система имеет бесчисленное множество решений. 123 332 zyx
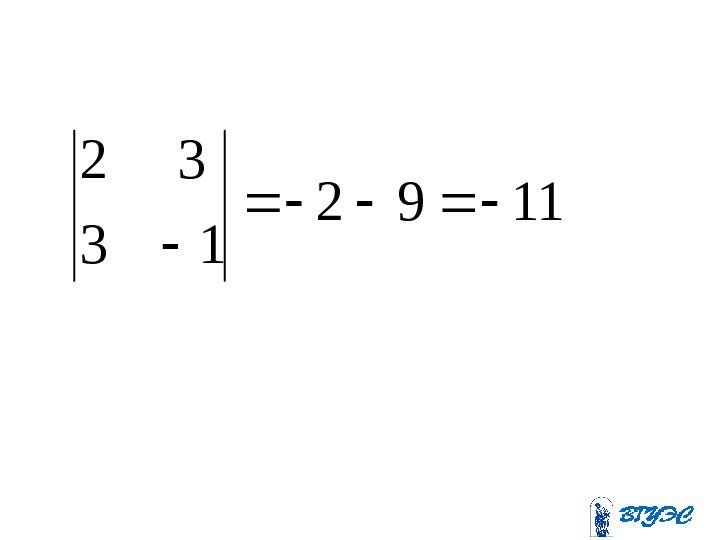
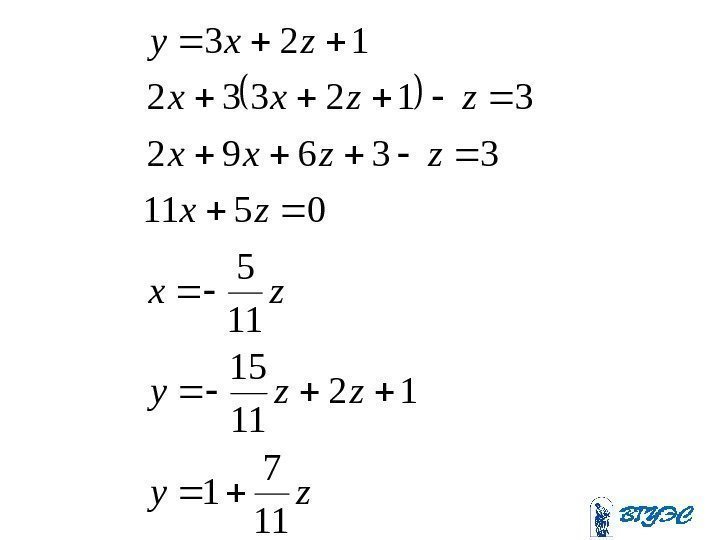 zy zx zx zzxx zxy
zy zx zx zzxx zxy
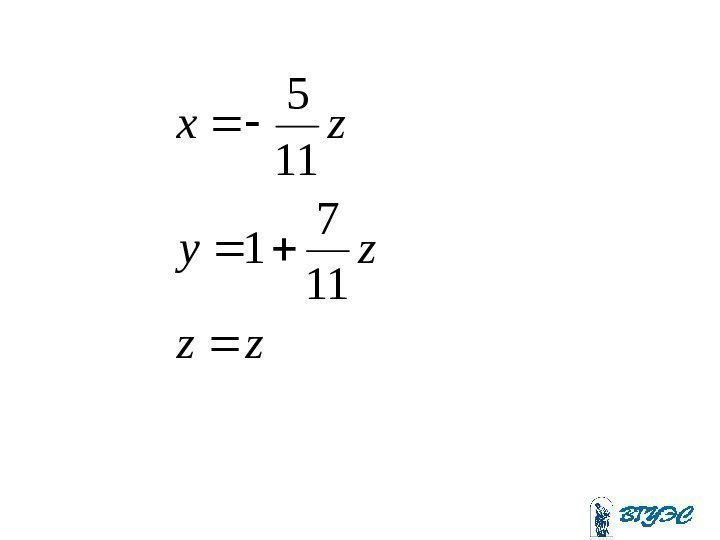 zz zy zx
zz zy zx
 Т е о р е м а К р о н е к е р а — К а п е л л и Для того чтобы система неоднородных линейных уравнений с неизвестными была совместной, необходимо и достаточно, чтобы m n Ar. Ar
Т е о р е м а К р о н е к е р а — К а п е л л и Для того чтобы система неоднородных линейных уравнений с неизвестными была совместной, необходимо и достаточно, чтобы m n Ar. Ar
 • Замечание. Пусть система совместна и — если число уравнений равно числу неизвестных, причем , то система имеет единственное решение; — если число уравнений меньше числа неизвестных, то система имеет множество решение. k. Ar 0 nk nk
• Замечание. Пусть система совместна и — если число уравнений равно числу неизвестных, причем , то система имеет единственное решение; — если число уравнений меньше числа неизвестных, то система имеет множество решение. k. Ar 0 nk nk
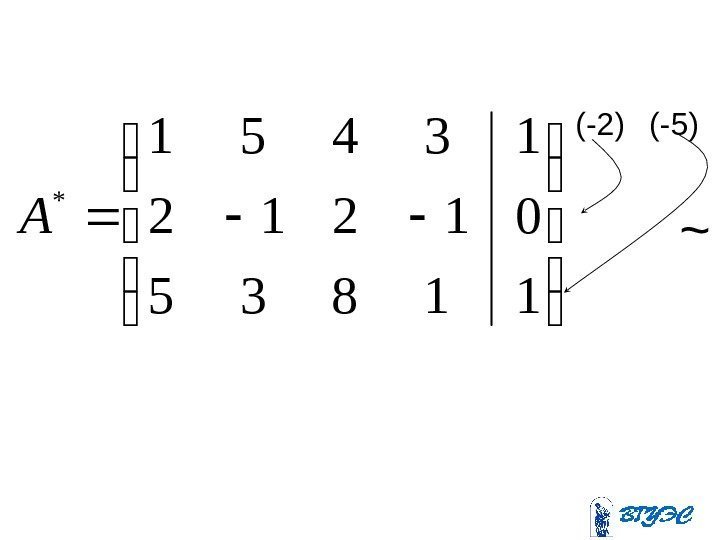
 (-2) (-5) 11835 01212 13451 * A ~
(-2) (-5) 11835 01212 13451 * A ~
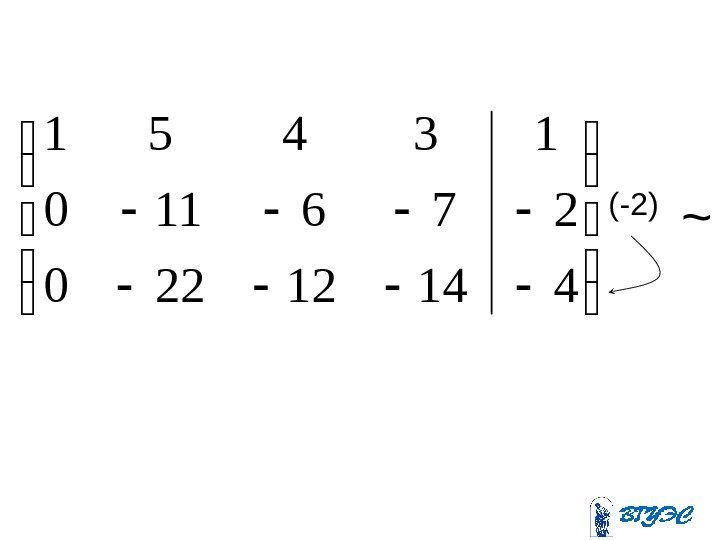 41412220 276110 13451 (-2) ~
41412220 276110 13451 (-2) ~
 00000 276110 1345142)()( * Ar. Ar
00000 276110 1345142)()( * Ar. Ar
 . 11 7 11 6 11 2 ; 11 2 11 14 11 1 432 431 xxx
. 11 7 11 6 11 2 ; 11 2 11 14 11 1 432 431 xxx
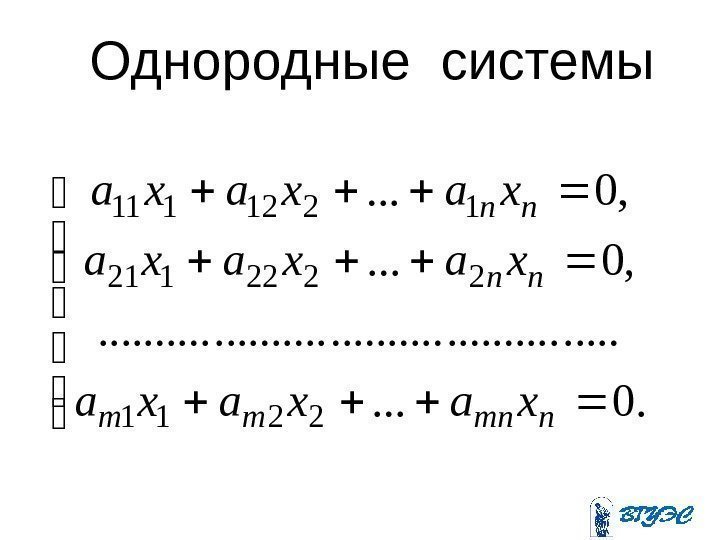 Однородные системы . 0. . . , 0. . . 2211 2222121 1212111 nmnmm nn nn xaxaxa
Однородные системы . 0. . . , 0. . . 2211 2222121 1212111 nmnmm nn nn xaxaxa
 Теорема о совместности однородной системы Для того чтобы однородная система линейных уравнений имела решение, необходимо и достаточно, чтобы ранг матрицы этой системы был меньше числа неизвестных n.
Теорема о совместности однородной системы Для того чтобы однородная система линейных уравнений имела решение, необходимо и достаточно, чтобы ранг матрицы этой системы был меньше числа неизвестных n.

