Системы координат и картографические проекции Значение координат

Системы координат и картографические проекции

Значение координат в геоинформационных системах Рассмотрение компьютерных моделей географических объектов позволяет выделить сущность представления реального мира в ГИС: модели географических объектов и их пространственные свойства – местоположение, форма, размеры, пространственные отношения – представляются посредством координат. Следовательно, и обработка географических данных в свою очередь связана с обработкой координат географических объектов. Таким образом, координаты являются базовым компонентом в моделях географических объектов. Для определения местоположения объектов на Земле используются системы координат, введенные для реального пространства Земли.

Земные сферы и сфероиды Физическая поверхность планеты Земля имеет сложную форму. Физическую модель фигуры Земли представляет геоид – уровенная поверхность, к которой отвесные линии всюду перпендикулярны и которая проходит через точку начала отсчета высот на среднем уровне океана.

Ученые из высшей технической школы Цюриха и геодезического института Мюнхена в середине 80 -х годов построили модель физической поверхности Земли в виде деформированной объемной фигуры на основании анализа спутниковых данных о силе земного притяжения в различных точках планеты Геоид

Геометрические модели Земли Сложную поверхность планеты Земля апроксимируют двумя геометрическими моделями: 1) сферой 2) сфероидом - эллипсоидом вращения, сжатым с полюсов. Выбор геометрической модели Земли зависит от цели решаемой задачи и необходимой точности результата вычислений.

Сфероиды и сферы

Представление Земли в виде сферы упрощает математические вычисления. Сфера основана на круге и описывается одним параметром – радиусом Земли. Земная сфера применяется в тех случаях, когда различие между сферой и сфероидом не существенно для точности результатов решения задачи. Например, при мелкомасштабном картографировании масштаба 1: 5 000 и меньше.

Представление Земли в виде сфероида связано со сложными математическими вычислениями и служит для вычислений геодезических широт, долгот, азимутов, длин, площадей, расчетов картографических проекций и решения других практических задач. Фигура Земли апроксимируется сфероидом для отображения поверхности Земли на картах масштаба 1: 1 000 и более крупных. Сфероид основан на эллипсе. Форма эллипса определена двумя радиусами - большой полуосью a и малой полуосью b.

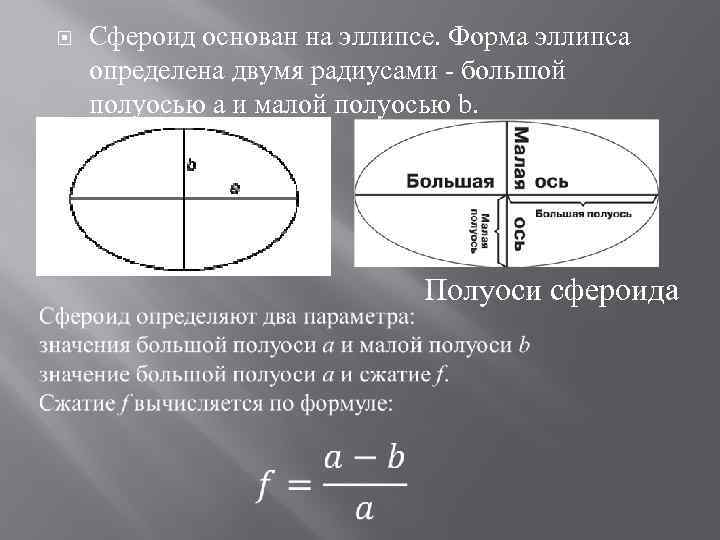Сфероид основан на эллипсе. Форма эллипса определена двумя радиусами - большой полуосью a и малой полуосью b. Полуоси сфероида

Сжатие характеризует различие в длинах полуосей. Сжатие может изменяться от нуля до единицы. Значение сжатия равное нулю означает, что эти две оси равны и образуют сферу. Сжатие сфероида Земли - маленькая величина, выражаемая десятичным числом (приблизительно равна 0, 003353). На основании геодезических измерений в разное время определен ряд сфероидов, которые представляют Землю. В таблице представлены некоторые сфероиды.

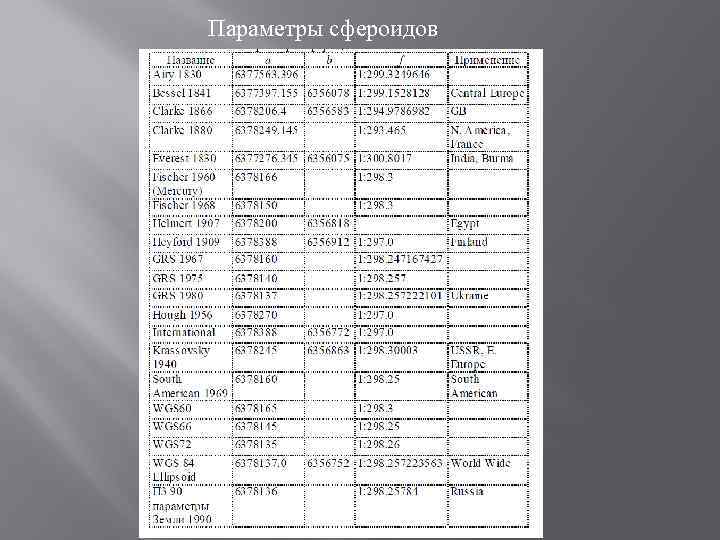Параметры сфероидов

Мировая геодезическая система WGS– 84 Системой пространственных прямоугольных координат, связанной с моделью Земли, является Мировая геодезическая система WGS 84 (World Geodetic System 1984). Она имеет широкое применение в связи с использованием спутниковых данных, получаемых в глобальной системе позиционирования GPS. Мировая геодезическая система WGS 84 была определена по спутниковым доплеровским (измеренные с помощью эффекта Доплера) измерениям в январе 1987 г. В последующие 1994 и 1996 годы WGS 84 была совершенствована за счет дополнительных точных спутниковых, геодезических и гравиметрических измерений.

Системы криволинейных координат Геодезическая система координат использует трехмерную сфероидическую поверхность, чтобы определить местоположения точек на Земле геодезическими координатами, которые в ГИС обозначаются φ, λ, h. Геодезическая широта φ точки – это угол между плоскостью экватора и нормалью к поверхности сфероида в точке. Геодезическая долгота λ точки – это угол между плоскостью начального меридиана и плоскостью геодезического меридиана точки. Геодезическая высота h точки – это длина отрезка нормали от сфероида до точки.

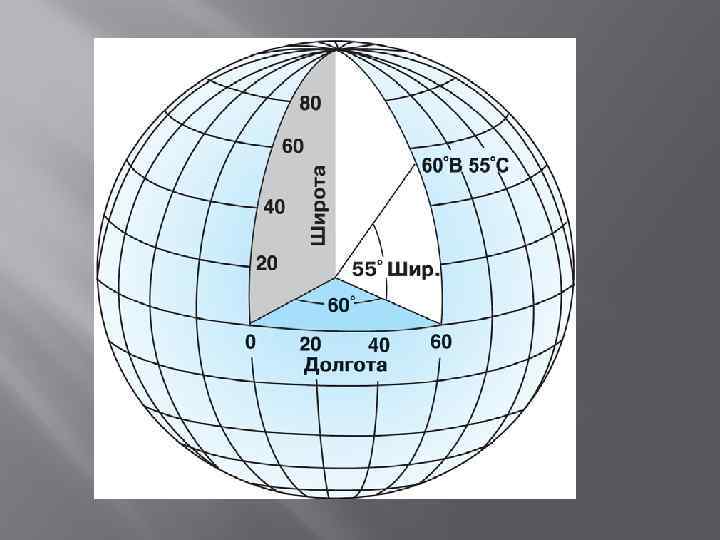
Кривыми координатными линиями являются меридианы и параллели. Меридиан - координатная линия, во всех точках которой долгота имеет постоянное значение. Параллель - координатная линия, для которой широта имеет постоянное значение. Эти координатные линии охватывают земной шар и формируют сеть параллелей и меридианов. Линия нулевой широты или максимальная параллель называется экватором. Линия нулевой долготы называется главным меридианом. Для большинства географических систем координат главный меридиан проходит через Гринвич (Greenwich) в Англии.

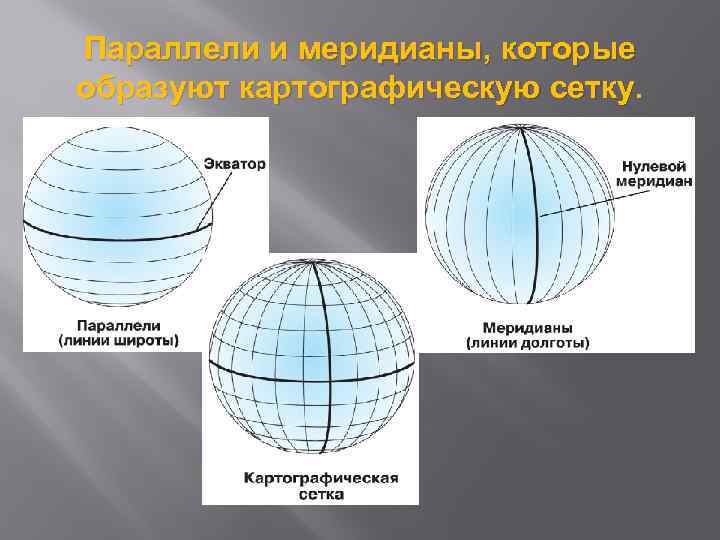Параллели и меридианы, которые образуют картографическую сетку.

Обозначение главного меридиана в Гринвичской обсерватории

Начало сетки параллелей и меридианов (0, 0) определено там, где пересекаются экватор и главный меридиан. Значения широты и долготы измеряются или в градусах, минутах, и секундах (degrees, minutes, and seconds - DMS), или в десятичных градусах. Значения 0 широты изменяются относительно экватора в диапазоне от -90° в Южном полюсе до +90° в Северном полюсе. Значения долготы изменяются относительно главного меридиана от -180° при перемещении на запад и до +180° при перемещении на восток. Долгота и широта могут иметь точные положения на поверхности земного шара.

Поскольку меридианы сходятся к полюсам, расстояние, представленное одним градусом долготы, не есть постоянная величина; оно уменьшается к полюсам. Так, например, на сфероиде Кларка 1866 один градус долготы в экваторе равняется 111. 321 км. (1° – 111 км. , 1' - 1. 85 км. , 1" – 31 м. ). На широте 60° один градус долготы равняется 55. 802 км. Так как градусы широты и долготы не имеют стандартную длину, для точного определения расстояния или площади требуются сложные математические зависимости.

Картографические проекции Картографической проекцией называется математическое преобразование трехмерной поверхности Земли, рассматриваемой как сфера или сфероид, на плоскость. Поверхность Земли проецируется на поверхность проецирования. В последующем поверхность проецирования развертывается в плоскость, для которой вводится проецированная система координат. В таких случаях поверхности проецирования называют развертывающимися поверхностями.

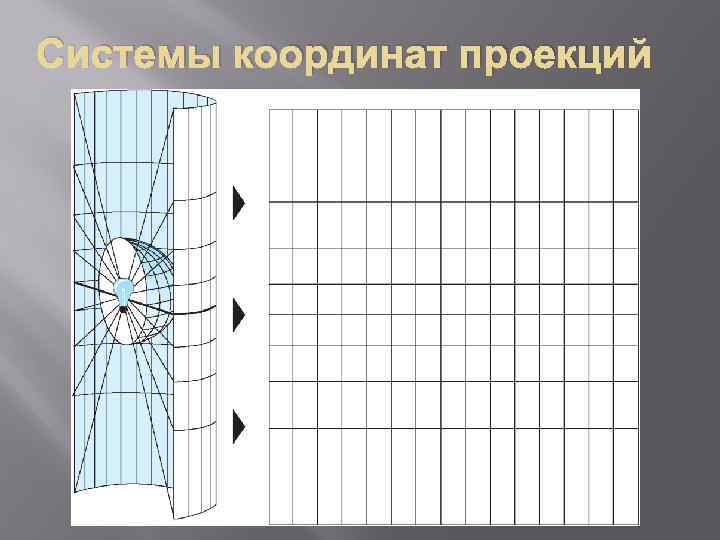Системы координат проекций

Картографическая проекция использует математические формулы, чтобы связать сфероидические/сферические координаты с плоскими плановыми координатами. В общем случае математическое преобразование представляется зависимостями: x = f 1(φ, λ) y = f 2(φ, λ)

В результате проецирования на плоскости получается искаженной сетка поверхности Земли. Это иллюстрация того, что сфера или сфероид не могут быть развернуты в любую плоскость без искажений. Представление поверхности Земли в двух измерениях приводит к искажениям формы, площади, расстояния или направления. Картографические проекции разработаны для определенных целей. Одна картографическая проекция может использоваться для крупномасштабных данных в ограниченной области, другая используется для мелкомасштабной карты мира. Картографические проекции, разработанные для мелкомасштабных данных, обычно основаны на сферических, а не на сфероидальных системах координат.

Классификация по типу искажений Конформные проекции Равноплощадные проекции Равнопромежуточные проекции Азимутальные проекции

Конформные проекции сохраняют локальную форму. Чтобы сохранять индивидуальные углы, описывающие пространственные отношения, конформная проекция должна показать перпендикулярные линии географической сетки, пересекающиеся на карте под углом 90 градусов. Картографическая проекция сохранет все углы. Отрицательная сторона проекции заключается в том, что площадь, ограниченная серией дуг, может быть значительно искажена в процессе. Никакая картографическая проекция не может сохранять формы больших областей.

Равноплощадные проекции сохраняют площадь отображенных пространственных объектов. Чтобы обеспечить это, другие свойства - форма, угол, и масштаб - искажаются. В равноплощадных проекциях меридианы и параллели не могут пересекаться под прямыми углами. В некоторых случаях, особенно на картах малых регионов, формы очевидно не искажены, и трудно отличить равноплощадную проекцию от конформной проекции без документирования или измерений.

Равнопромежуточные проекции сохраняют расстояния между определенными точками. Любой проекцией масштаб не поддерживается корректно везде в полной карте. Однако, в большинстве случаев имеются одна или большее число линий на карте, по которым масштаб поддерживается правильно. Большинство проекций, сохраняющих расстояния, имеют одну или большее количество линий, для которых длина линии на карте является той же самой длиной (в масштабе карты), как такой же самой линии на земном шаре. Такие расстояния считаются истинными и отвечают истинному масштабу между двумя точками на карте.

Азимутальные проекции Самый короткий маршрут между двумя точками на кривой поверхности Земли проходит по сферическому эквиваленту прямой линии на плоской поверхности. Это - большой круг, проходящий через две точки. Проекции истинного направления (True-direction projections) или азимутальные проекции содержат некоторые дуги большого круга, представляющие направления или азимуты всех точек на карте правильно относительно центра.

Классификация по типу проецирования Цилиндрическая Коническая Плоская

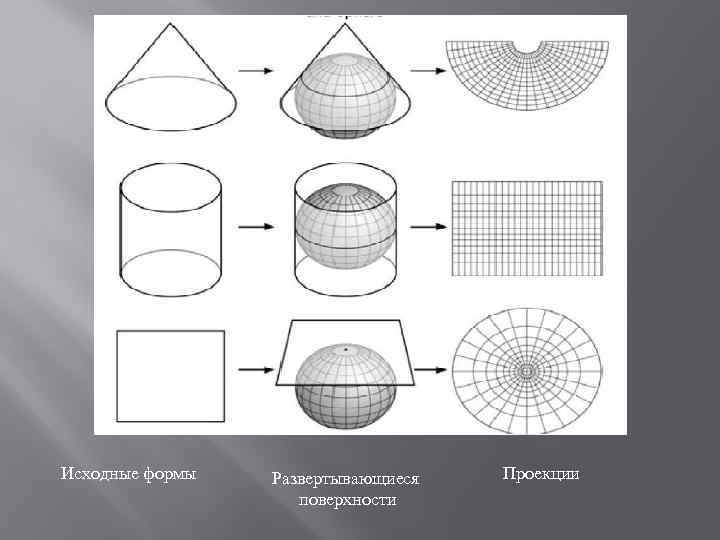Исходные формы Развертывающиеся поверхности Проекции

Поверхности проецирования - конусы, цилиндры и плоскости могут принимать нормальное, поперечное или наклонное положение относительно оси вращения сферы или сфероида.

Коническая проекция Конические проекции используют конус как поверхность проецирования. Наиболее простая коническая проекция касательная к земному шару по параллели. Эта линия является стандартной параллелью. Меридианы проецируются на коническую поверхность, соединяясь в вершине или точке конуса. Параллели проецируются на конус как кольца. Конус затем разрезается по любому меридиану и развертывается в плоскость. Заключительная коническая проекция имеет прямо сходящиеся линии для меридианов и концентрические дуги окружностей для параллелей. Противоположный линии разреза меридиан становится центральным меридианом. С удалением от стандартной параллели искажения становятся большими. Конические проекции используются для зон средних широт, которые имеют восточно-западную ориентацию, и не используются для полярных областей.

Секущие конические проекции определены двумя стандартными параллелями. Модель искажений для секущих проекций разная между стандартными параллелями и за ними. Секущая проекция имеет меньшие искажения, чем касательная проекция. Если ось конуса не совмещают с полярной осью земного шара, такие типы проекций называются перспективными.

Цилиндрическая проекция Цилиндрические проекции используют цилиндр как поверхность проецирования. Подобно коническим проекциям, цилиндрические проекции могут также быть секущими или касательными. Ось цилиндра может располагаться по оси вращения эллипсоида, в плоскости экватора, наклонно к оси вращенияэллипсоида.

При размещении оси цилиндра по оси вращения эллипсоида создается нормальная цилиндрическая проекция. Примером является проекция Меркатора, у которой экватор является ее линией касания. Сечения геометрически проецируются на цилиндрическую поверхность, а параллели математически проецируются. Этим создается координатная сетка с углами 90 градусов. Цилиндр разрезается по любому меридиану, чтобы построить конечную цилиндрическую проекцию.

Плоские проекции (Planar projections) используют плоскость как поверхность проецирования. Плоская проекция также известна как азимутальная проекция или зенитальная проекция. Плоскость может быть касательной к земному шару в одной точке, или может быть секущей. Точкой касания может быть Полярный Полюс, Южный Полюс, точка на экваторе или любая точка между ними. Возможные положения поверхности проецирования: полярное, экваториальное и наклонное (косое).