Системы дифференциальных уравнений Общие понятия
Системы дифференциальных уравнений ¡ Нормальные системы Д. У. l Система уравнений вида l с неизвестными функциями l называется нормальной системой дифференциальных уравнений. l
Системы дифференциальных уравнений ¡ ¡ ¡ Решением системы Д. У. называется вектор-функция определенная в , имеющая там производную первого порядка и такая, что при подстановке ее и ее производных в систему каждое уравнение превращается в тождество. Производной вектор- функции называется вектор-функция
Системы дифференциальных уравнений ¡ ¡ Задача Коши для системы Д. У. : найти решение системы такое , что в некоторой точке оно удовлетворяет начальному условию
Системы дифференциальных уравнений ¡ Векторная запись системы Д. У. ¡ Обозначим: ¡ Получим векторное уравнение ¡ ¡ ¡ Решение векторного уравнения – это вектор-функция , удовлетворяющая векторному уравнению:
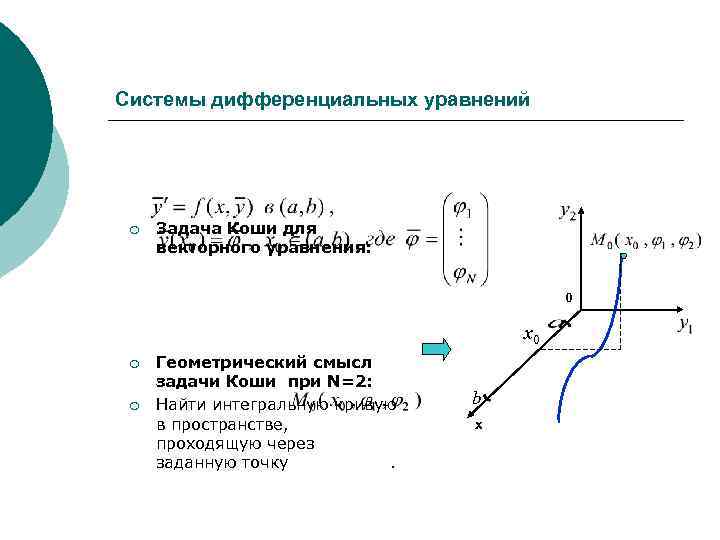
Системы дифференциальных уравнений ¡ Задача Коши для векторного уравнения: 0 x 0 ¡ ¡ Геометрический смысл задачи Коши при N=2: Найти интегральную кривую в пространстве, проходящую через заданную точку. b х
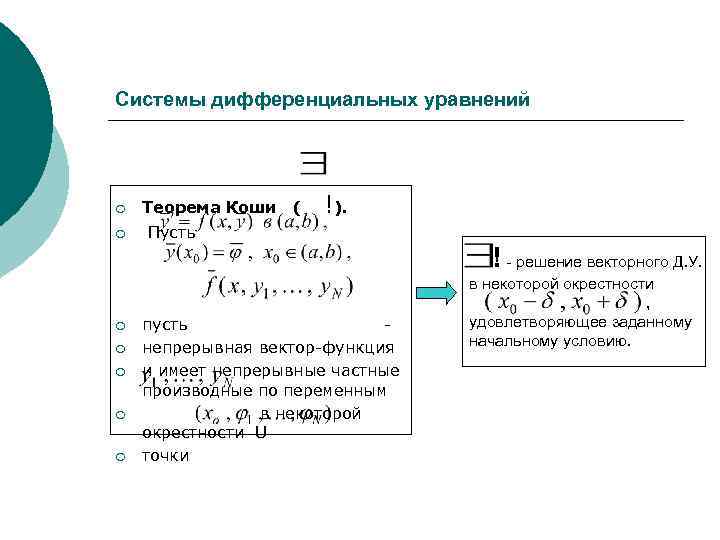
Системы дифференциальных уравнений ¡ ¡ ¡ ¡ Теорема Коши ( !). Пусть пусть непрерывная вектор-функция и имеет непрерывные частные производные по переменным в некоторой окрестности U точки ! - решение векторного Д. У. в некоторой окрестности , удовлетворяющее заданному начальному условию.
Скачать презентацию Системы дифференциальных уравнений Общие понятия Системы дифференциальных
Lection_19.ppt