Системи штучного інтелекту Лекція 3 Генетичні алгоритми 1

Системи штучного інтелекту Лекція 3. Генетичні алгоритми 1

Загальний підхід • генетичні алгоритми виникли в результаті спостереження і спроб копіювання природних процесів, що відбуваються в світі живих організмів, зокрема, еволюції та пов'язаної з нею селекції (природнього відбору) популяцій живих істот. 2

Історичні факти • Ідею генетичних алгоритмів висловив Дж. Холланд у кінці шістдесятих — початку сімдесятих років XX століття. • Він працював над алгоритмами, що оперували послідовностями двійкових цифр (одиниць і нулів), що одержали назву хромосом. Ці алгоритми імітували еволюційні процеси в поколіннях таких хромосом. У них були реалізовані механізми селекції та репродукції, аналогічно вживаними природній еволюції. 3

Генетичні алгоритми і традиційні методи оптимізації • Генетичні алгоритми — це процедури пошуку, засновані на механізмах природного відбору і спадкоємства. У них використовується еволюційний принцип виживання найбільш пристосованих особин. Вони відрізняються від традиційних методів оптимізації декількома базовими елементами. Зокрема, генетичні алгоритми: – обробляють не значення параметрів самого завдання, а їх закодовану форму; – здійснюють пошук рішення виходячи не з єдиної точки, а з їх деякої популяції; – використовують тільки цільову функцію, а не її похідні або іншу додаткову інформацію; – застосовують імовірнісні, а не детерміновані правила вибору. 4

Основні поняття генетичних алгоритмів • • Популяція — це кінцева множина особин. Особини, що входять в популяцію, у генетичних алгоритмах представляються хромосомами з закодованими в них множинами параметрів задачі, тобто рішень, які інакше називаються точками в просторі пошуку (search points). У деяких роботах особини називаються організмами. Хромосоми (інші назви — ланцюжки або кодові послідовності) — це впорядковані послідовності генів. Ген (який також називається властивістю, знаком чи детектором) — це атомарний елемент генотипу, зокрема, хромосоми. Генотип або структура — це набір хромосом даної особини. Отже, особинами популяції можуть бути генотипи або одиничні хромосоми (в досить поширеному випадку, коли генотип складається з однієї хромосоми). Фенотип — це набір значень, які відповідає даному генотипу, тобто декодована структура або безліч параметрів задачі (розв’язок, точка простору пошуку). Алель — це значення конкретного гена, також визначається як значення властивості або варіант властивості. Локус чи позиція вказує місце розміщення даного гена в хромосомі (ланцюжку). Множина позицій генів — це локи. 5

Основні поняття генетичних алгоритмів • Дуже важливим поняттям у генетичних алгоритмах вважається функція пристосованості (fitness function), яка інакше називається функцією оцінки. Вона являє міру пристосованості даної особини в популяції. Ця функція відіграє найважливішу роль, оскільки дозволяє оцінити ступінь пристосованості конкретних особин у популяції і вибрати з них найбільш пристосовані (тобто мають найбільші значення функції пристосованості) відповідно з еволюційним принципом виживання «найсильніших» (які найкраще пристосувалися). • На кожній ітерації генетичного алгоритму пристосованість кожної особини даної популяції оцінюється за допомогою функції пристосованості, і на цій основі створюється наступна популяція особин, що складають безліч потенційних рішень проблеми, наприклад, задачі оптимізації. Чергова популяція в генетичному алгоритмі називається поколінням, а до новостворюваної популяції особин застосовується термін «нове покоління» або «покоління нащадків» . 6

Приклад використання ГА • f(х) = 2 х2 +1, х = 1. . 15 • Задача оптимізації цієї функції полягає в переміщені в просторі, який складається з 16 точок зі значеннями 0, 1, …, 15 для виявлення тієї точки, в якій функція приймає максимальне (або мінімальне) значення. 7

Приклад використання ГА • В цьому випадку в ролі параметра задачі виступає змінна х. Множина {0, 1, . . . , 15} складає простір пошуку та одночасно — множину потенціальних розв’язків задачі. Кожне з 16 чисел, які належать цій множині, називається точкою простору пошуку, розв’язком, значенням параметра, фенотипом. Розв’язок, який оптимізує функцію, називається найкращим або оптимальним розв’язком. Значення параметра х від 0 до 15 можна закодувати наступним чином: • 0000 0001 0010 0011 0100 0101 0110 0111 • 1000 1001 1010 1011 1100 1101 1110 1111 • Пристосованість окремих хромосом в популяції визначається значенням цієї функції для значень х, які відповідають цим хромосомам, тобто для фенотипів, які відповідають певним генотипам. 8

Класичний ГА Основний (класичний) генетичний алгоритм (який також називається елементарним чи простим генетичним алгоритмом) складається з наступних кроків: – ініціалізація, або вибір вихідної популяції хромосом; – оцінка пристосованості хромосом в популяції; – перевірка умови зупинки алгоритму; – селекція хромосом; – застосування генетичних операторів; – формування нової популяції; – вибір «найкращої» хромосоми. 9

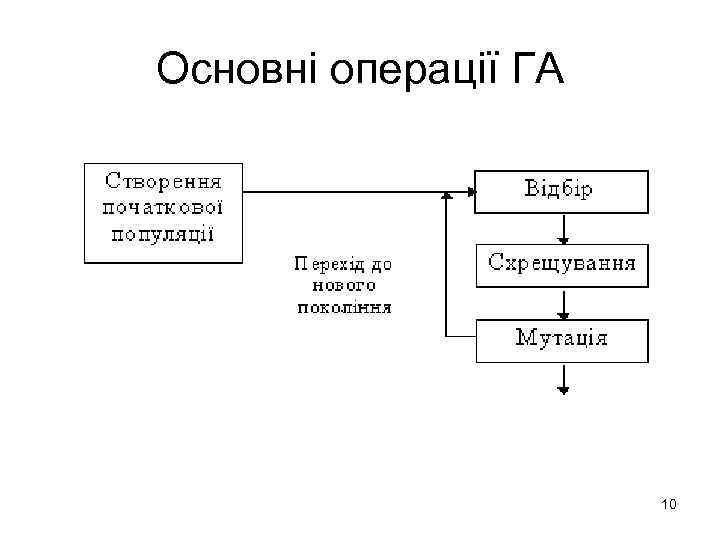Основні операції ГА 10

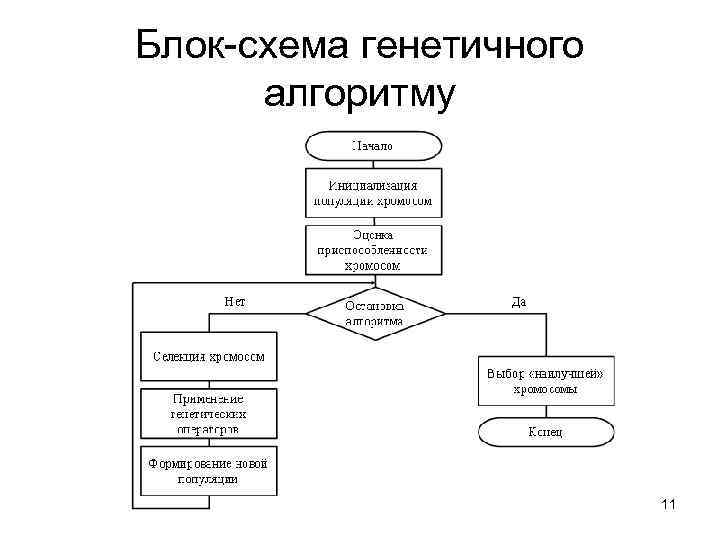Блок-схема генетичного алгоритму 11

Перевірка умови зупинки алгоритму • Визначення умови зупинки генетичного алгоритму залежить від його конкретного застосування. У оптимізаційних задачах, якщо відомо максимальне (або мінімальне) значення функції пристосованості, то зупинка алгоритму може відбутися після досягнення очікуваного оптимального значення, можливо — з заданою точністю. • Зупинка алгоритму також може статися у разі, коли його виконання не приводить до поліпшення вже досягнутого значення. Алгоритм може бути зупинений після закінчення певного часу виконання або після виконання заданої кількості ітерацій. Якщо умова зупинки виконана, то проводиться перехід до завершального етапу вибору «найкращої» хромосоми. В іншому випадку на наступному кроці виконується селекція. 12

Селекція хромосом • Селекція хромосом полягає у виборі (по розрахованим на другому етапі значеннями функції пристосованості) тих хромосом, які братимуть участь у створенні нащадків для наступної популяції, тобто для чергового покоління. Такий вибір здійснюється згідно з принципом природного добору, за яким найбільші шанси на участь у створенні нових особин мають хромосоми з найбільшими значеннями функції пристосованості. • Існують різні методи селекції. Найбільш популярним вважається так званий метод рулетки, який свою назву отримав за аналогією з відомою азартною грою. Кожній хромосомі може бути зіставлений сектор колеса рулетки, величина якого встановлюється пропорційною значенню функції пристосованості даної хромосоми. Тому чим більше значення функції пристосованості, тим більше сектор на колесі рулетки. 13

Схема виконання генетичного алгоритму 14

Метод рулетки • Все колесо рулетки відповідає сумі значень функції пристосованості всіх хромосом розглянутої популяції. Кожній хромосомі, що позначається chi для і =1, 2, …, N (де N позначає чисельність популяції) відповідає сектор колеса V(сhj), виражений у відсотках згідно з формулою 15

Метод рулетки • Селекція хромосоми може бути представлена як результат повороту колеса рулетки, оскільки хромосома «яка виграла» (тобто обрана) відноситься до сектору цього колеса, що випав. • Очевидно, що чим більше сектор, тим більше вірогідність «перемоги» відповідної хромосоми. Тому ймовірність вибору даної хромосоми виявляється пропорційною значенню її функції пристосованості. Якщо все коло колеса рулетки представити у вигляді цифрового інтервалу [0, 100], то вибір хромосоми можна ототожнити з вибором числа з інтервалу [a, b], де а і b позначають відповідно початок і закінчення фрагмента кола, відповідного цьому сектору колеса; очевидно, що 0 <а < b <100. 16

Перехід до наступних кроків ГА • В результаті процесу селекції створюється батьківська популяція, також звана батьківським пулом (matingpool) з чисельністю N, що дорівнює чисельності поточної популяції. • Застосування генетичних операторів до хромосом, відібраних за допомогою селекції, призводить до формування нової популяції нащадків від створеної на попередньому кроці батьківської популяції. • У класичному генетичному алгоритмі застосовуються два основних генетичних оператора: оператор схрещування (сrossover) та оператор мутації (mutation). Однак слід зазначити, що оператор мутації грає явно другорядну роль в порівнянні з оператором схрещування. Це означає, що схрещування в класичному генетичному алгоритмі здійснюється практично завжди, тоді як мутація — досить рідко. Вірогідність схрещування, як правило, досить велика (звичайно 0, 5 <рc <1), тоді як імовірність мутації встановлюється дуже малою (найчастіше 0 <рm <0, 1). Це випливає з аналогії зі світом живих організмів, де мутації відбуваються надзвичайно рідко. 17

Оператор схрещування • • На першому етапі схрещування вибираються пари хромосом з батьківського популяції (батьківського пулу). Це тимчасова популяція, що складається з хромосом, відібраних в результаті селекції та призначених для подальших перетворень операторами схрещування і мутації з метою формування нової популяції нащадків. На даному етапі хромосоми з батьківського популяції об'єднуються в пари. Це здійснюється випадковим способом відповідно до ймовірністю схрещування Pс. Далі для кожної пари відібраних таким чином батьків розігрується позиція гена (локус) у хромосомі, що визначає так звану точку схрещування. Якщо хромосома кожного з батьків складається з L генів, то очевидно, що точка схрещування Lк представляє собою натуральне число, менше L. Тому фіксація точки схрещування зводиться до випадкового вибору числа з інтервалу [1, L-1] У результаті схрещування пари батьківських хромосом виходить така пара нащадків: нащадок, хромосома якого на позиціях від 1 до Lк складається з генів першого з батьків, а на позиціях від Lк + 1 до L — із генів другого з батьків; нащадок, хромосома якого на позиціях від 1 до Lк складається з генів другого з батьків, а на позиціях від Lк + 1 до L — з генів першого з батьків. 18

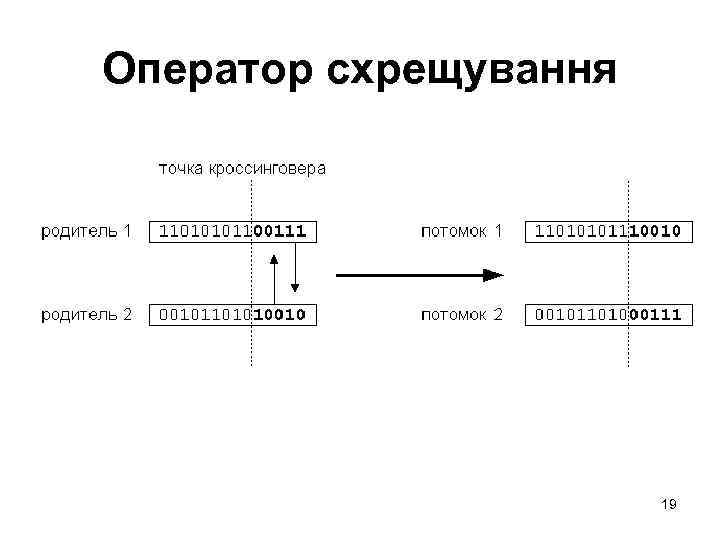Оператор схрещування 19

Оператор мутації • Оператор мутації з імовірністю рm змінює значення гена в хромосомі на протилежне (тобто з 0 на 1 або навпаки). Наприклад, якщо в хромосомі [10011010] мутації піддається ген на позиції 7, то його значення, рівне 1, змінюється на 0. що призводить до утворення хромосоми [100110001010]. Як вже згадувалося вище, ймовірність мутації зазвичай дуже мала, і саме від неї залежить, чи буде цей ген мутувати чи ні. Вірогідність рm мутації може емулюватися, наприклад, випадковим вибором числа з інтервалу [0, 1] для кожного гена і відбором для виконання цієї операції тих генів, для яких розігране число виявляється меншим або рівним значенню рm. 20

Ілюстрація виконання класичного генетичного алгоритму • Розглянемо сильно спрощений і досить штучний приклад, що складається в знаходженні хромосоми з максимальною кількістю одиниць. Припустимо, що хромосоми складаються з 12 генів, а популяція налічує 8 хромосом. Зрозуміло, що найкращою буде хромосома, що складається з 12 одиниць. Подивимося, як протікає процес вирішення цієї вельми тривіальної задачі за допомогою генетичного алгоритму. 21

Ілюстрація виконання класичного генетичного алгоритму • Ініціалізація, або вибір вихідної популяції хромосом. Необхідно випадковим чином згенерувати 8 двійкових послідовностей довжиною 12 бітів. Це можна досягти, наприклад, підкиданням монети (96 разів, при випаданні «орла» приписується значення 1, а у разі «решки» — 0). Таким чином можна сформувати вихідну популяцію ch 1 = [11100101] ch 5 = [010001100100] ch 2= [00111010] ch 6 = [010011000101] ch 3 = [01110011] ch 7 = [101011011011] ch 4 = [00101000] ch 8 = [000010111100] 22

Ілюстрація виконання класичного генетичного алгоритму • Оцінка пристосованості хромосом в популяції. У спрощеному прикладі, що розглядається, вирішується задача знаходження такої хромосоми, яка містить найбільшу кількість одиниць. Тому функція пристосованості визначає кількість одиниць у хромосомі. Позначимо функцію пристосованості символом F. Тоді її значення для кожної хромосоми з вихідної популяції будуть такі: F(ch 1) = 7 F(ch 5)= 4 F(ch 2) = 6 F(ch 6) = 5 F(ch 3) = 8 F(ch 7) = 8 F(ch 4) = 3 F(ch 8) = 5 • Хромосоми ch 3 і ch 7 характеризуються найбільшими значеннями функції приналежності. У цій популяції вони вважаються найкращими кандидатами на рішення задачі. 23

Ілюстрація виконання класичного генетичного алгоритму • Селекція хромосом. Селекція проводиться методом рулетки. На підставі формул (1. 2) і (1. 3) для кожної з 8 хромосом поточної популяції (у нашому випадку — вихідної популяції, для якої N = 8) отримуємо сектори колеса рулетки, виражені у відсотках v(ch 1) = 15, 22 v(ch 2) = 13, 04 v(ch 3) = 17, 39 v(ch 4) =6, 52 v(ch 5) =8, 70 v(ch 6) = 10, 87 v(ch 7) = 17, 39 v(ch 8) = 10, 87 24

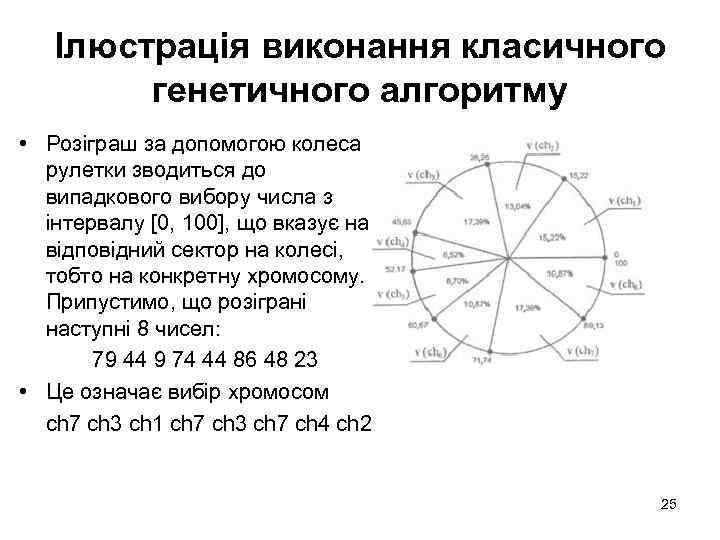Ілюстрація виконання класичного генетичного алгоритму • Розіграш за допомогою колеса рулетки зводиться до випадкового вибору числа з інтервалу [0, 100], що вказує на відповідний сектор на колесі, тобто на конкретну хромосому. Припустимо, що розіграні наступні 8 чисел: 79 44 9 74 44 86 48 23 • Це означає вибір хромосом ch 7 ch 3 ch 1 ch 7 ch 3 ch 7 ch 4 ch 2 25

Ілюстрація виконання класичного генетичного алгоритму • Припустимо, що ні одна з відібраних у процесі селекції хромосом не піддається мутації, і всі вони складають популяцію хромосом, призначених для схрещування. Це означає, що ймовірність схрещування Pс = 1, а ймовірність мутації рm = 0. Припустимо, що з цих хромосом випадковим чином сформовані пари батьків ch 2 и ch 7 ch 1 и ch 7 ch 3 и ch 4 ch 3 и ch 7 26

Ілюстрація виконання класичного генетичного алгоритму • Для першої пари випадковим чином вибрана точка схрещування lk = 4, для другої lk = 3, для третьої lk = 11, для четвертої lk = 5. В результаті виконання оператора схрещування виходять 4 пари нащадків. 27

Ілюстрація виконання класичного генетичного алгоритму • Формування нової популяції. Після виконання операції схрещування ми отримуємо наступну популяцію нащадків: Ch 1 = [001111011011] Ch 5 = [01110010] Ch 2 = [101000111010] Ch 6 = [00101001] Ch 3 = [111011011011] Ch 7 = [011101011011] Ch 4 = [10100101] Ch 8 = [101011110011] 28

Ілюстрація виконання класичного генетичного алгоритму • Оцінки пристосованості хромосом з новосформованої популяції, яка стає поточною. Значення функцій пристосованості хромосом цієї популяції складають: F(Ch 1) = 8 F(Ch 5) = 7 F(Ch 2) = 6 F(Ch 6) = 4 F(Ch 3) = 9 F(Ch 7) = 8 F(Ch 4) = 6 F(Ch 8) = 8 • Помітно, що популяція нащадків характеризується набагато більш високим середнім значенням функції пристосованості, ніж популяція батьків. Звернемо увагу, що в результаті схрещування отримана хромосома Ch 3 з найбільшим значенням функції пристосованості, яким не володіла ні одна хромосома з батьківського популяції. 29

Загальний програмний алгоритм ГА 30

Теорія “sheme” • Хоча зовні здається, що ГА обробляє рядки, насправді при цьому неявно відбувається обробка шим (“sheme”), що представляють шаблони подоби між рядками. ГА практично не може займатися повним перебором усіх представлень у просторі пошуку. 31

Теорія “sheme” • Шима - це рядок довжиною l (що дорівнює довжині будь-якого рядка популяції), що складається зі знаків алфавіту {0; 1; *}, де {*} - невизначений символ. 32

Теорія “sheme” • Кожна шима визначає безліч усіх бінарних рядків довжини l, що мають у відповідних позиціях або 0, або 1, у залежності від того, який біт знаходиться у відповідній позиції самої шими. • Наприклад, шима, 1**01, визначає собою множину з чотирьох п’ятибітових рядків {10001; 10101; 11001; 11101}. • У шим виділяють дві властивості - порядок і визначена довжина. Порядок шими - це число визначених бітів ("0" чи "1") у шимі. 33

Теорія “sheme” • Визначена довжина - відстань між крайніми визначеними бітами у шимі. Наприклад, вищезгадана шима має порядок o(1**01)=3, а визначена довжина d(1**01) = 4. Кожен рядок у популяції являється прикладом 2 l шим. 34

Теорія “sheme” • Будуючі блоки - це шими, що мають такі властивості, як високу пристосованість, низький порядок, коротку визначену довжину. • Пристосованість шими визначається, як середнє серед пристосованостей прикладів, котрі її містять. Після процедури відбору залишаються лише строки с найбільш високою пристосованістю. 35

Теорія “sheme” • Нехай m(H, t) - число прикладів шими H у t-ому поколінні. Обчислимо очікуване число прикладів H у наступному поколінні m(H, t+1) у термінах m(H, t). Простий ГА кожному рядку ставить у відповідність імовірність її "виживання" при відбиранні пропорційно її пристосованості. Очікується, що шима H може бути обрана m(H, t)*(f(H)/fср. ) разів, де fср. - середня пристосованість популяції, а f(H) - середня пристосованість тих рядків у популяції, що є прикладами H. 36

Геометрична інтерпретація теорії “sheme” • Розглянемо на прикладі простої одномірної функції f(x) процедуру переходу з евклідова простору параметрів в простір представлень. f(x) = 10 + x cos(x), на відрізку [0, 10]. 37

Геометрична інтерпретація теорії “sheme” • Нехай кодування буде здійснюватися бінарними рядками довжини 3. Тобто відрізок [0, 10] потрібно розбити на 23 = 8 підінтервалів, кожному з яких буде відповідати унікальна двійкова комбінація, одержувана перекладом номера підінтервала, рахуючи зліва направо, у двійковій позиційній системі. Довжина кожного такого інтервалу буде h=10: 8=1, 25. 38

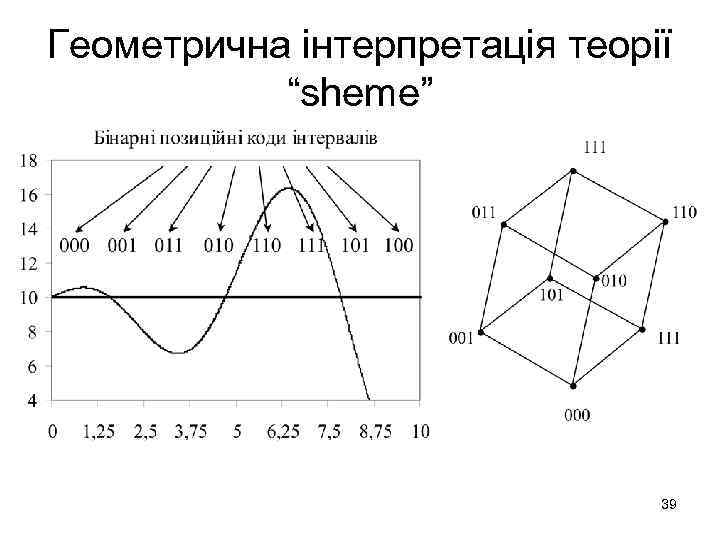Геометрична інтерпретація теорії “sheme” 39

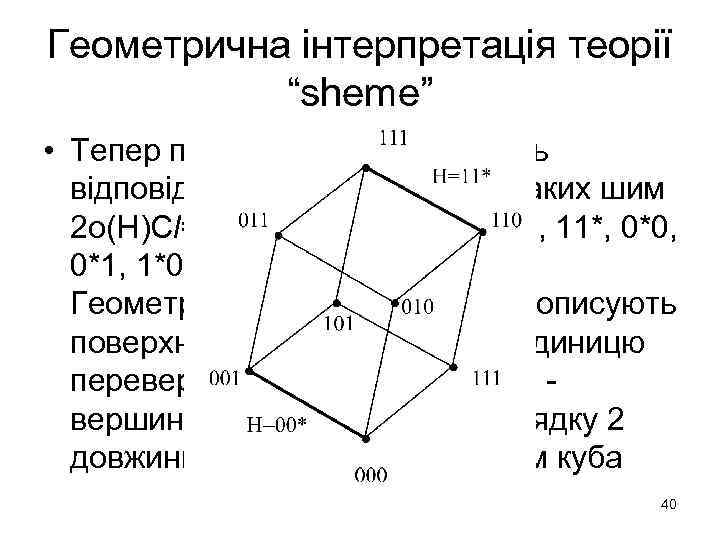Геометрична інтерпретація теорії “sheme” • Тепер подивимося, чому будуть відповідати шими порядку 2. Таких шим 2 o(H)Cl=22 C 3=12: {00*, 01*, 10*, 11*, 0*0, 0*1, 1*0, 1*1, *00, *01, *10, *11}. Геометрично, усі такі шаблони описують поверхні, розмірність яких на одиницю перевершує розмірність крапки - вершини куба, тобто шими порядку 2 довжини 3 відповідають ребрам куба 40

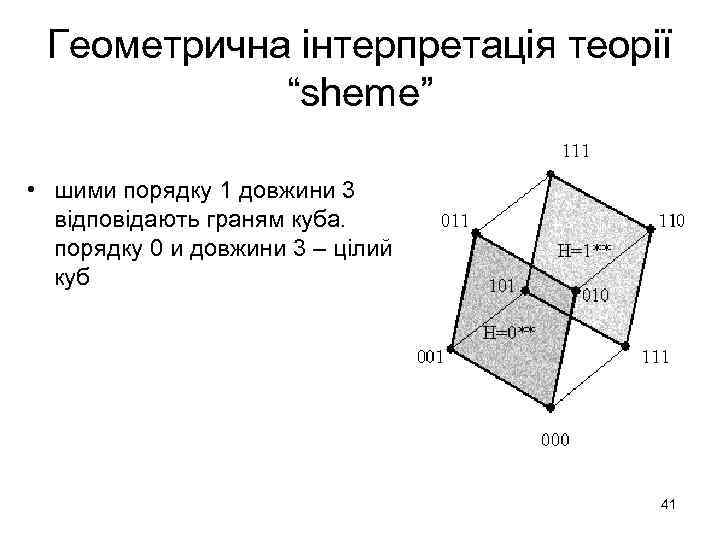Геометрична інтерпретація теорії “sheme” • шими порядку 1 довжини 3 відповідають граням куба. порядку 0 и довжини 3 – цілий куб 41

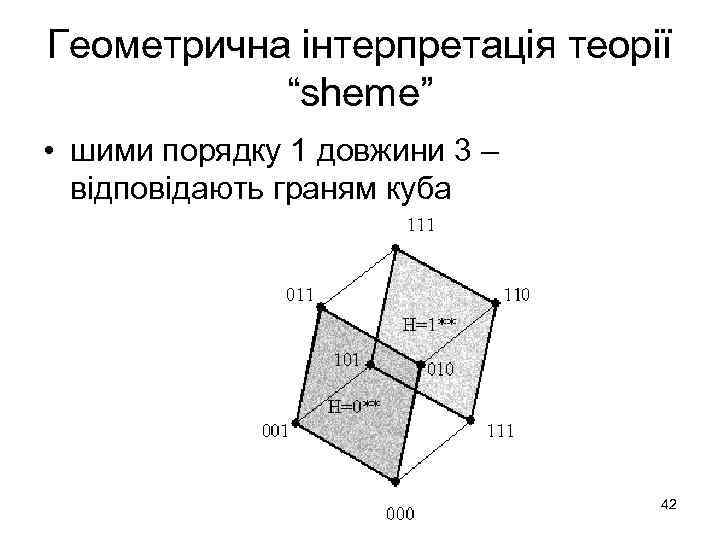Геометрична інтерпретація теорії “sheme” • шими порядку 1 довжини 3 – відповідають граням куба 42

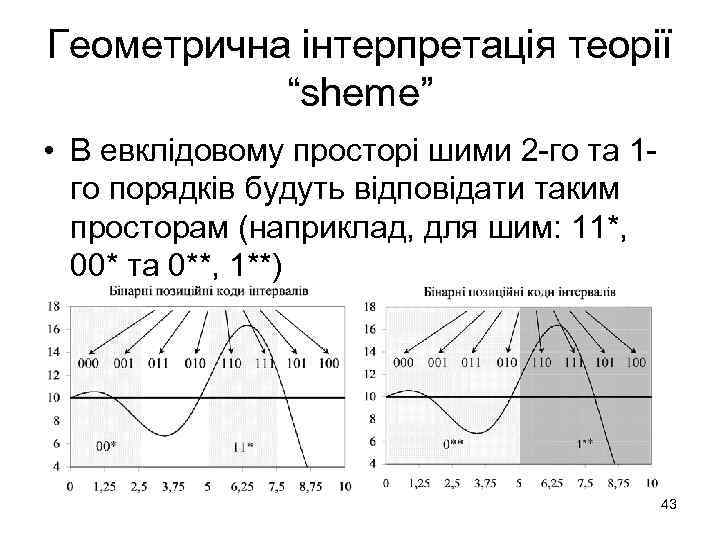Геометрична інтерпретація теорії “sheme” • В евклідовому просторі шими 2 -го та 1 го порядків будуть відповідати таким просторам (наприклад, для шим: 11*, 00* та 0**, 1**) 43

Переваги та недоліки ГА • Переваги генетичних алгоритмів – не вимагають жодної інформації про поверхні відповіді; – розриви, існуючі на поверхні відповіді мають незначний ефект на повну ефективність оптимізації; – стійки до потрапляння в локальні оптимуми; – добре працюють при вирішенні великомасштабних проблем оптимізації; – можуть бути використані для широкого класу задач; – прості і прозорі в реалізації; – можуть бути використані в задачах з мінливим середовищем. • ГА не бажано використовувати: – – у разі, коли необхідно знайти точний глобальний оптимум; при великому часі обчислення функції; необхідно знайти всі рішення задачі, а не одне з них; конфігурація не є простою (вимагає кодування рішення). 44

Корисні посилання • http: //www. gotai. net/documents/doc-imp 005. aspx - ГА на C# • http: //matlab. exponenta. ru/fuzzylogic/book 5/1_2. php - ГА на Mat. Lab • http: //www. aiportal. ru/articles/geneticalgorithms/algorithm-example. html - приклад розв’язку задачі 45

Дякую за увагу! 46