Система счисления совокупность приемов наименования и записи

Система счисления – совокупность приемов наименования и записи чисел Базисные числа – символы, используемые для записи чисел Основание системы – количество базисных чисел системы счисления позиционные 352, 23 величина числа зависит от номера позиции цифры при его записи непозиционные VII, XIX каждой цифре соответствует величина, не зависящая от ее места в записи числа

непозиционные системы счисления Период палеолита. 10 -11 тысяч лет до н. э. § Единичная ( «палочная» ) или см. пример 2, 5 тысяч лет до н. э. § Древнеегипетская десятичная непозиционная система = 345 - единицы - десятки - сотни

непозиционные системы счисления 2 тысячи лет до н. э. § Вавилонская шестидесятеричная цифры: и - единицы - десятки - 60 ; 602 ; 603 ; … ; 60 n = 33 = 60 + 2 = 82 2 -ой разряд 1 -ый разряд пример

=384 = 3600 + 30 + 2 = 3632 пропущенный шестидесятичный разряд Шестидесятеричная вавилонская система – первая известная нам система счисления, основанная на позиционном принципе.

непозиционные системы счисления § Римская система 500 лет до н. э. Цифры: I V X L C D M 1 5 10 50 100 500 1000 Число формировалось из цифр, а также с помощью групп: Группа 1 -го вида - несколько одинаковых подряд идущих цифр: XX = 20 Группа 2 -го вида - разность значений двух цифр, если слева стоит меньшая: СМ = 1000 – 100 = 900 Величина числа суммируется из значений цифр и групп 1 -го или 2 -го вида: X X X I I = 32 D X L I I = 542

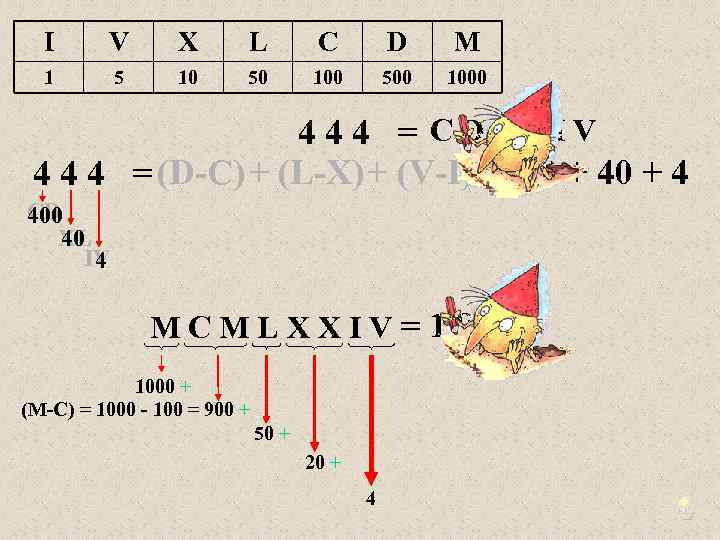I V X L C D M 1 5 10 50 100 500 1000 444 = CDXLIV 4 4 4 = (D-C)+ (L-X)+ (V-I) = 400 + 4 CD 400 XL 40 IV 4 MCMLXXIV=1974 1000 + (M-C) = 1000 - 100 = 900 + 50 + 20 + 4

непозиционные системы счисления § Алфавитные системы 1 2 3 4 5 6 7 8 9 10 «Фита» «Веди» «Земля» «Иже» «И» «Аз» «Глаголь» «Добро» «Есть» «Зело» - титло «… В год 6367. Варяги из заморья взимали дань…» ( «Повесть временных лет» ) - тысячи - тьма: х10 000 = 10 000 100 000 - легион 1000. . . - леодр 000 1050 - колода «более сего несть человеческому уму разумевати»

позиционные системы счисления Позиционной называют систему счисления, в которой число представляется в виде последовательности цифр, количественное значение которых зависит от места (позиции), которое занимает каждая из них в числе. 1000 100 (103) (102) 10 1 4 позиция 1 (100) 1 3 позиция (102)позиция х1 х 1000 1235 Десятичная система: 1, 10, счисления…–, 10 n 102, 103, Базис позиционной системы2 3 Двоичная система: чисел, каждое из 2 n это последовательность 1, 2, 2 , … , P-ичнаязадает значение -n, …, p «по -1, p 0, p 1 и … , pn система: …, p цифры -2, p месту» , которых «вес» каждого разряда. p – основание системы

позиционные системы счисления § Традиционные: P-ичные Базис системы – геометрическая прогрессия с основанием p: …, p-2, p-1, p 0, p 1, p 2, p 3, p 4, p 5, … Десятичная система Пример: 25310 Основание: 10 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Базис: …, 10 -2, 10 -1, 1, 102, 103, … , 10 n • Почему в записи § Нетрадиционные числа в Фибоначчиевая система Базис: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … фибоначчиевой Алфавит: 0, 1 системе не могут Пример: 10000100 ф = 3 + 34 =3710 стоять две единицы подряд? § Смешанные: P-Q-ичные Каждая цифра числа, заданного в Q-ичной системе, заменяется ее представлением в P-ичной системе. Двоично-десятичная система 3580910 = 0011 0101 1000 0000 10012 -10

позиционные системы счисления В любой традиционной P-ичной позиционной системе счисления число равно сумме степеней основания: 147, 20510 = 1 100 + 4 10 + 7 1 + 2 0, 1 + 0 0, 01 + 5 0, 001 = = 1 102 + 4 101+7 100+2 10 -1 + 0 10 -2 + 5 10 -3 Xp = an…a 1 a 0, b-1…b-k. . . P X = an. Pn + an-1 Pn-1 + … +a 1 P + a 0 + b-1 P-1 + b-2 P-2 + … + b-k. P-k + … Арифметические действия над числами во всех P-ичных системах счисления выполняются одинаково. ( + )

Двоичная система счисления p=2 – основание системы; 0, 1 – алфавит …, ¼, ½, 1, 2, 4, 8, 16, 32, … – базис (…, 2 -2, 2 -1, 20, 21, 22, 23, 24, 25, …) Перевод из двоичной системы счисления в десятичную: Лейбниц, изрядное 41 1 0 0 1(Leibniz)0 Готфрид+ 0 22 + 1 23 + 0 24 + 1 25 = 1 + 8 + 32 = время = 1 2 + 0 21 10 Лейбниц 2 уделивший двоичной Вильгельм 25 24 23 22 21(1646 -1716) 20 немецкий философ, математик, физик, языковед (бинарной) математике, видел в ней «… прообраз творения» . см. слайд Он считал, что «единица С конца ХХ века, века компьютеризации, человечество пользуется двоичной системой + 32 =1+4 1001012 = 1 + 0 21 + 1 22 + 0 23 + 0 24 + 1 25 представляет = 3710 ежедневно, так как вся информация, божественное начало, а обрабатываемая ЭВМ, хранится в них= 2 – 8 + 32 = 4210 в 1010102 = 0 + 1 21 + 0 22 + 1 23 + 0 24 + 1 25 ноль + небытие. Высшее двоичном 2 виде. 4 Существо создает все 1 8 16 32 64 128 20 21 22 23 24 25 сущее из небытия точно 26 27 таким же образом, как

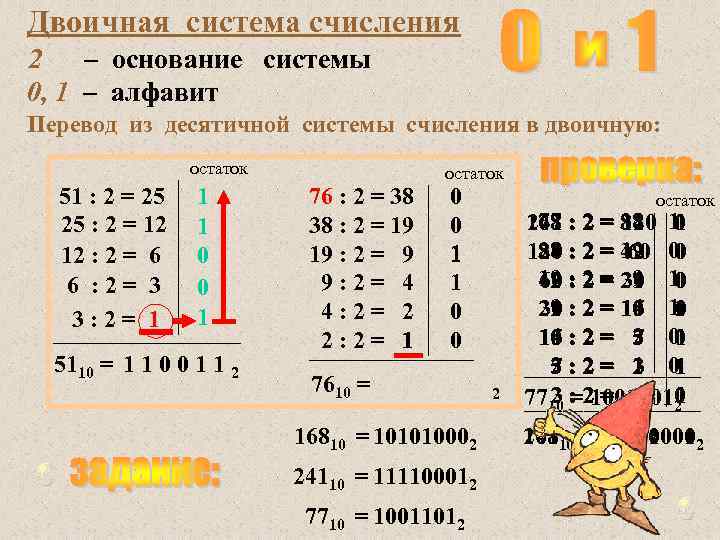Двоичная система счисления 2 – основание системы 0, 1 – алфавит Перевод из десятичной системы счисления в двоичную: остаток 51 : 2 = 25 25 : 2 = 12 12 : 2 = 6 6 : 2= 3 3: 2= 1 1 1 0 0 1 5110 = 1 1 0 0 1 1 2 76 : 2 = 38 38 : 2 = 19 19 : 2 = 9 9: 2= 4 4: 2= 2 2: 2= 1 остаток 0 0 1 1 0 0 7610 = 16810 = 101010002 24110 = 111100012 7710 = 10011012 остаток 2 77 38 0 168 : 2 = 84 11 241 120 38 19 0 120 : 2 = 42 0 84 60 19 : 2 = 21 1 9 42 60 30 0 9 4 21 : 2 = 10 10 30 15 1 4 2 0 10 : 2 = 5 01 15 7 2 5: 2= 1 0 7 2 1 3 2= = 1 2 3 1 7710 : 210011010 241 16810 = 101010002 11110001