Скачать презентацию SISTEM SATU FASA EET 103 TEKNOLOGI ELEKTRIK Скачать презентацию SISTEM SATU FASA EET 103 TEKNOLOGI ELEKTRIK

992b38678738d295a963dff3cdfff968.ppt

  • Количество слайдов: 114

SISTEM SATU FASA EET 103 TEKNOLOGI ELEKTRIK SISTEM SATU FASA EET 103 TEKNOLOGI ELEKTRIK

SISTEM SATU FASA • Pengenalan dan ciri-ciri sistem satu fasa • Kebaikan dan keburukan SISTEM SATU FASA • Pengenalan dan ciri-ciri sistem satu fasa • Kebaikan dan keburukan sistem satu fasa • Pengiraan voltan, arus dan kuasa

PENGENALAN DAN CIRI-CIRI SISTEM SATU FASA • ALTERNATING CURRENT: a current or voltage varies PENGENALAN DAN CIRI-CIRI SISTEM SATU FASA • ALTERNATING CURRENT: a current or voltage varies periodically in magnitude and direction

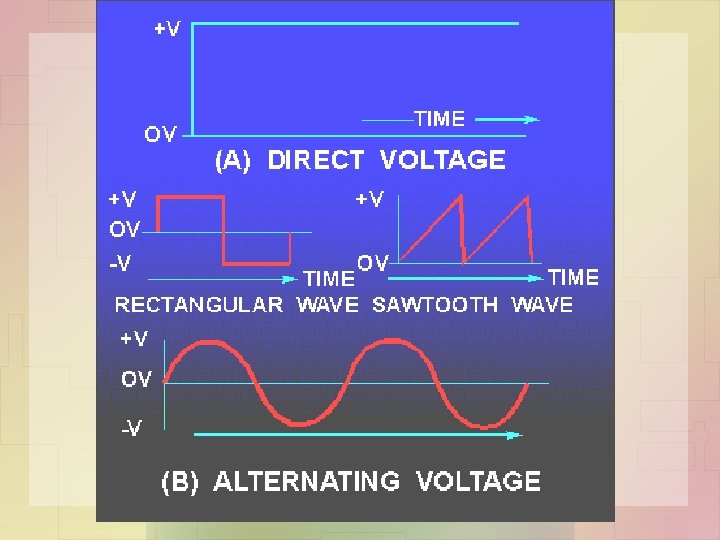
PERBEZAAN AC DAN DC Difference between DC and AC: • DC: a direct flow PERBEZAAN AC DAN DC Difference between DC and AC: • DC: a direct flow of electrons through a conductor such as a metal wire. A battery or DC generator usually provides a source of electrons and the potential or voltage between the positive (+) and negative (-) terminals.

• AC (Alternating Current): a back-and-forth movement of electrons in a wire. When • AC (Alternating Current): a back-and-forth movement of electrons in a wire. When the force of a negative (-) charge is at one end of a wire and a positive (+) potential is at the other end, the electrons in the wire will move away from the (-) charge, just like in DC electricity. But if the charges at the ends of the wires are suddenly switched, the electrons will reverse their direction.

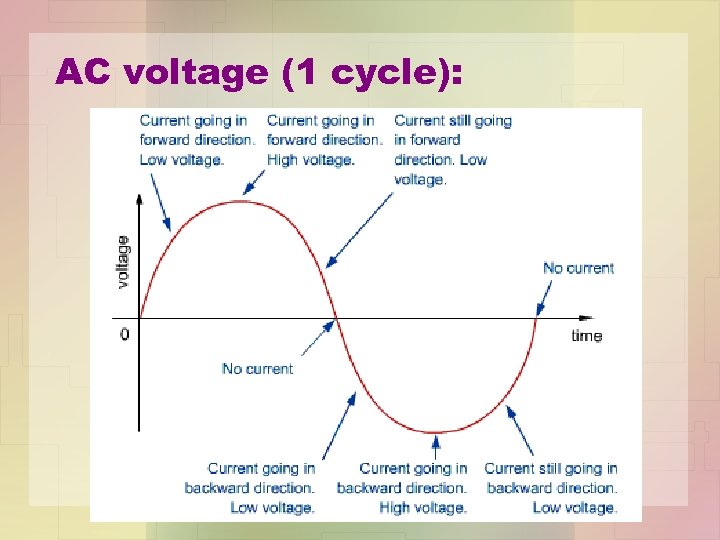AC voltage (1 cycle): AC voltage (1 cycle):

Mathematics of AC voltages • An AC voltage v(t) can be described mathematically as Mathematics of AC voltages • An AC voltage v(t) can be described mathematically as a function of time by the following equation: where A is the amplitude in volts (also called the peak voltage), ω is the angular frequency in radians per second t is the time in seconds

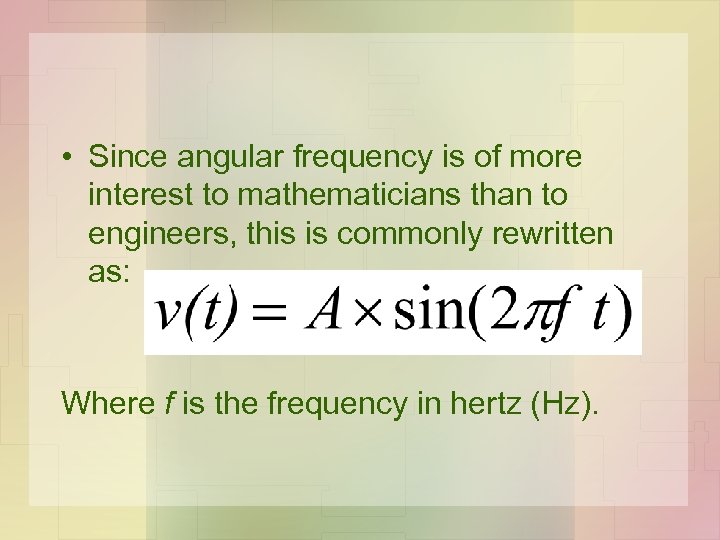• Since angular frequency is of more interest to mathematicians than to engineers, • Since angular frequency is of more interest to mathematicians than to engineers, this is commonly rewritten as: Where f is the frequency in hertz (Hz).

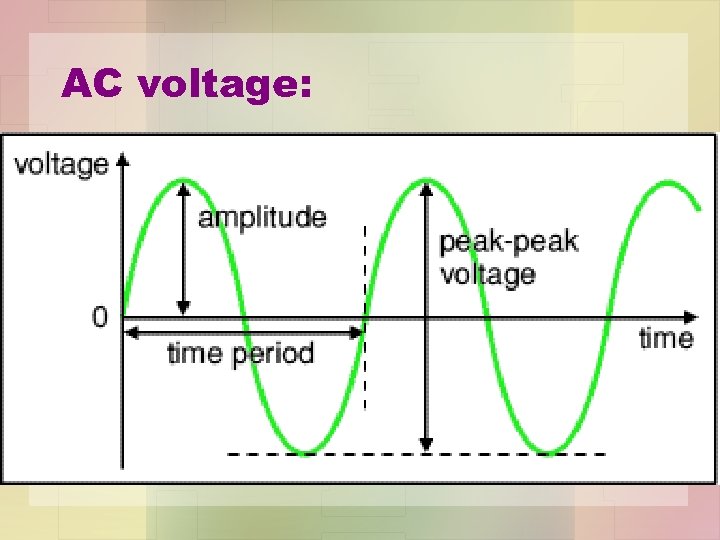AC voltage: AC voltage:

• Amplitude is the maximum voltage reached by the signal. It is measured • Amplitude is the maximum voltage reached by the signal. It is measured in volts, V. • Peak voltage (Vp) is another name for amplitude. • Peak-peak voltage (Vp-p) is twice the peak voltage (amplitude). When reading an oscilloscope trace it is usual to measure peak-peak voltage.

RMS (effective) value: • The root-mean-square (RMS) value of an alternating current is the RMS (effective) value: • The root-mean-square (RMS) value of an alternating current is the steady direct current which converts electrical energy to other forms of energy in a given resistance at the same rate as the alternating current (AC). • In power distribution work the AC voltage is nearly always given in as a root-mean-square (rms) value, written Vrms. For a sinusoidal voltage:

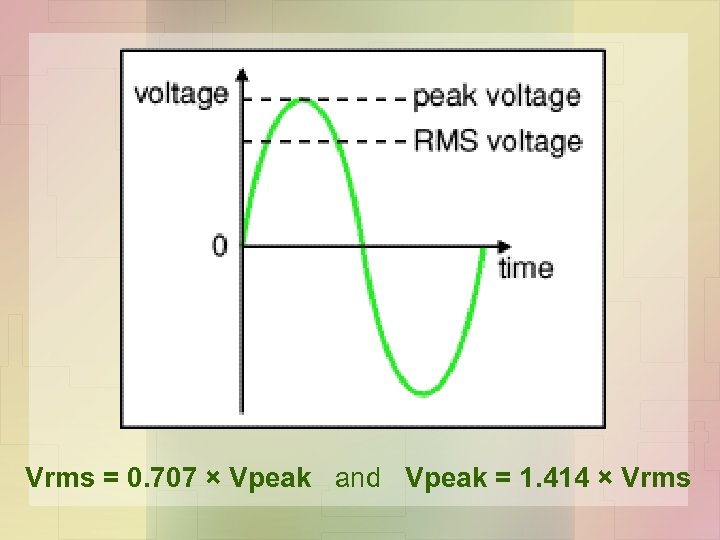Vrms = 0. 707 × Vpeak and Vpeak = 1. 414 × Vrms Vrms = 0. 707 × Vpeak and Vpeak = 1. 414 × Vrms

Frequency • The number of complete cycles of alternating current or voltage completed each Frequency • The number of complete cycles of alternating current or voltage completed each second • Frequency is always measured and expressed in hertz (Hz).

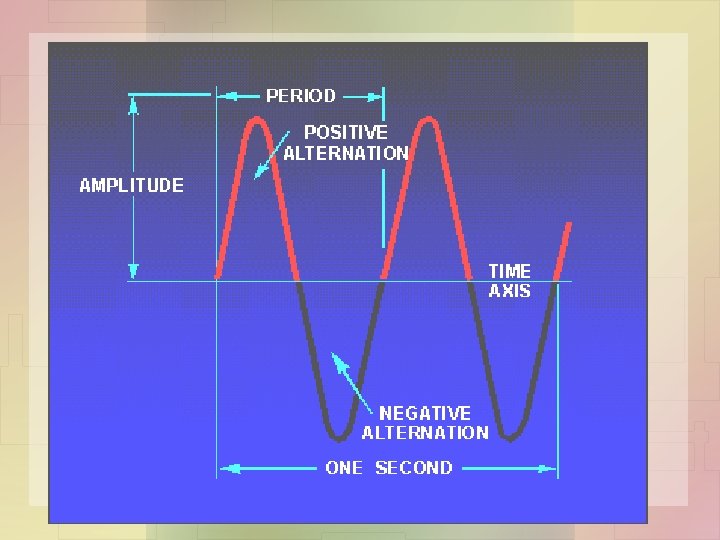
Period • An individual cycle of any sine wave represents a definite amount of Period • An individual cycle of any sine wave represents a definite amount of TIME. • The time required to complete one cycle of a waveform is called the PERIOD of the wave. • The relationship between Period (T) in seconds and frequency (f) in Hz:

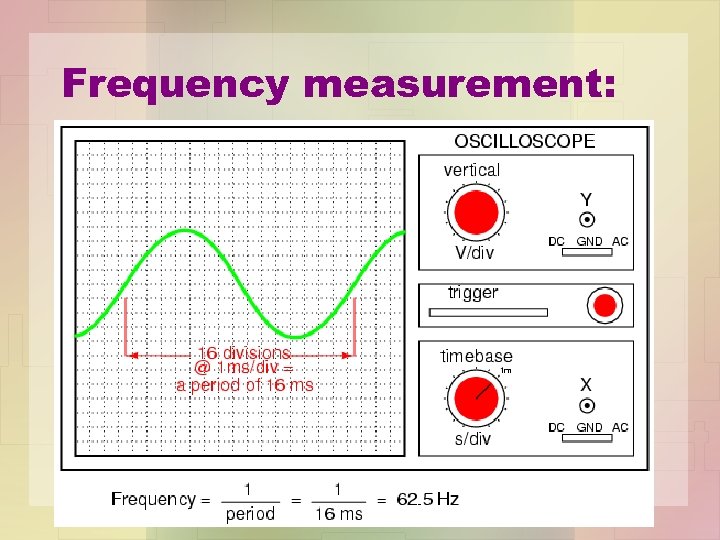Frequency measurement: Frequency measurement:

Wavelength • The time it takes for a sine wave to complete one cycle Wavelength • The time it takes for a sine wave to complete one cycle is defined as the period of the waveform. The distance traveled by the sine wave during this period is referred to as WAVELENGTH.

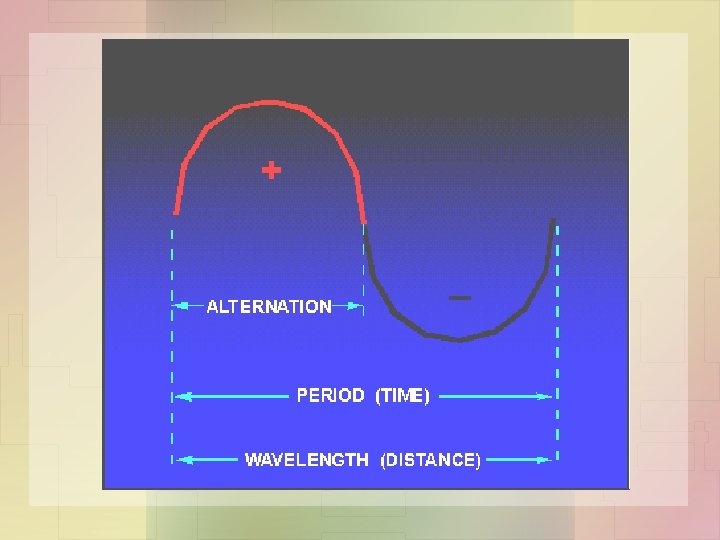
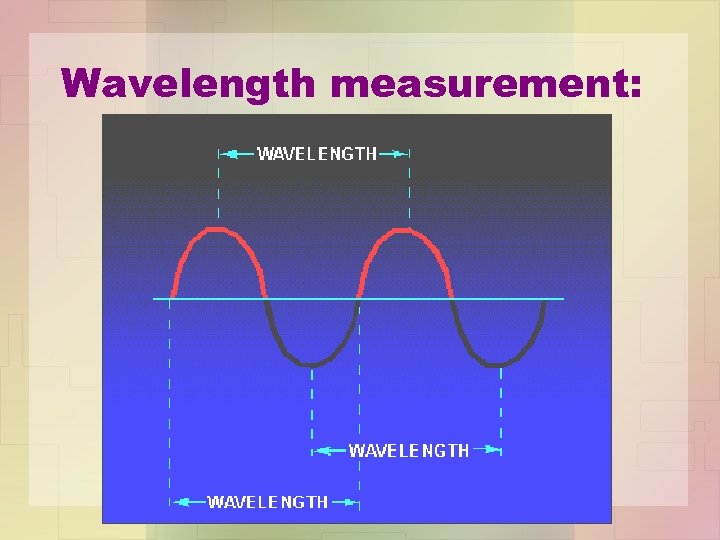Wavelength measurement: Wavelength measurement:

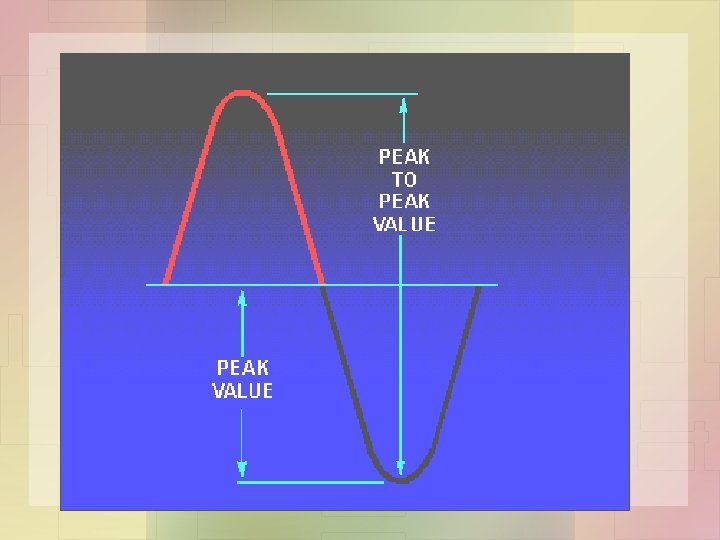
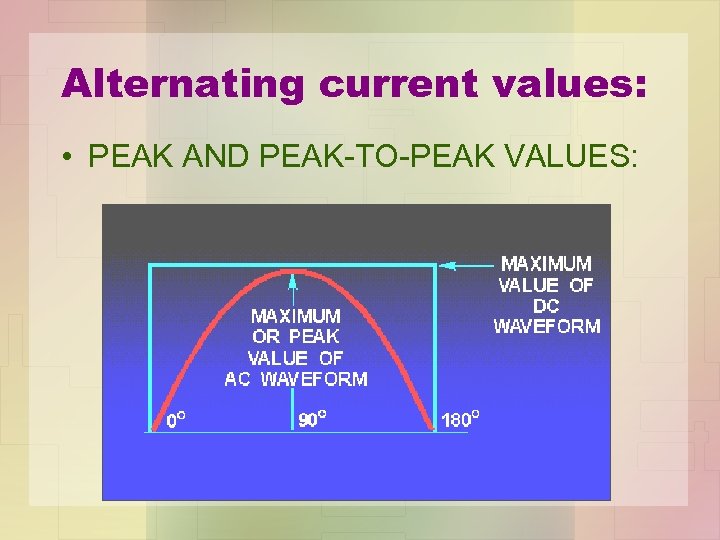Alternating current values: • PEAK AND PEAK-TO-PEAK VALUES: Alternating current values: • PEAK AND PEAK-TO-PEAK VALUES:

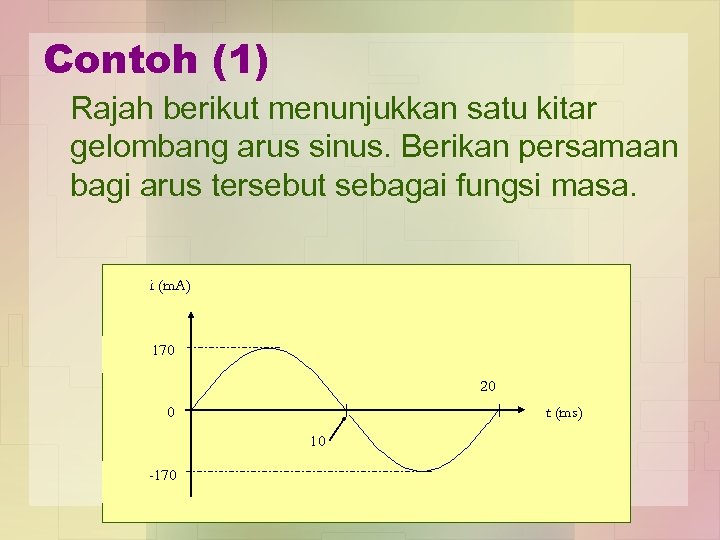Contoh (1) Rajah berikut menunjukkan satu kitar gelombang arus sinus. Berikan persamaan bagi arus Contoh (1) Rajah berikut menunjukkan satu kitar gelombang arus sinus. Berikan persamaan bagi arus tersebut sebagai fungsi masa. i (m. A) 170 20 0 t (ms) 10 -170

Penyelesaian: • Persamaan umum bagi gelombang sinus ialah i(t) = Im sin t • Penyelesaian: • Persamaan umum bagi gelombang sinus ialah i(t) = Im sin t • Dari rajah gelombang diketahui; Im = 170 m. A dan T = 20 ms = 0. 02 s

• Maka, frekuensi dapat dikira seperti berikut: f = 1/T = 1/0. 02 • Maka, frekuensi dapat dikira seperti berikut: f = 1/T = 1/0. 02 = 50 Hz • Seterusnya persamaan arus menjadi, i(t) = Imsin t = 170 sin(2 ft) = 170 sin(100 t) m. A

Contoh (2) Satu voltan ulang-alik bentuk sin mempunyai frekuensi 2500 Hz dan nilai puncak Contoh (2) Satu voltan ulang-alik bentuk sin mempunyai frekuensi 2500 Hz dan nilai puncak 15 V. Lukiskan bentuk satu kitar gelombang voltan tersebut.

Penyelesaian • Dari soalan, diketahui nilai-nilai berikut: Vm = 15 V dan T = Penyelesaian • Dari soalan, diketahui nilai-nilai berikut: Vm = 15 V dan T = 0. 4 ms • Rajah umum gelombang sinus adalah seperti berikut: v (V) 15 0. 4 0 t (ms) 0. 2 -15

Contoh (3) Satu voltan ulang-alik sinus diberikan oleh persamaan: v(t) = 156 kos(800 t)V Contoh (3) Satu voltan ulang-alik sinus diberikan oleh persamaan: v(t) = 156 kos(800 t)V Lukiskan rajah satu kitar gelombang voltan tersebut.

Penyelesaian: Diberi, v(t) = Vm kos( t) = 156 kos(800 t) volt Maka, nilai Penyelesaian: Diberi, v(t) = Vm kos( t) = 156 kos(800 t) volt Maka, nilai puncak voltan, Vm = 156 = 2 f = 800 f = 400 Tempoh bagi gelombang ini ialah; T = 1/f = 1/400 = 2. 5 ms

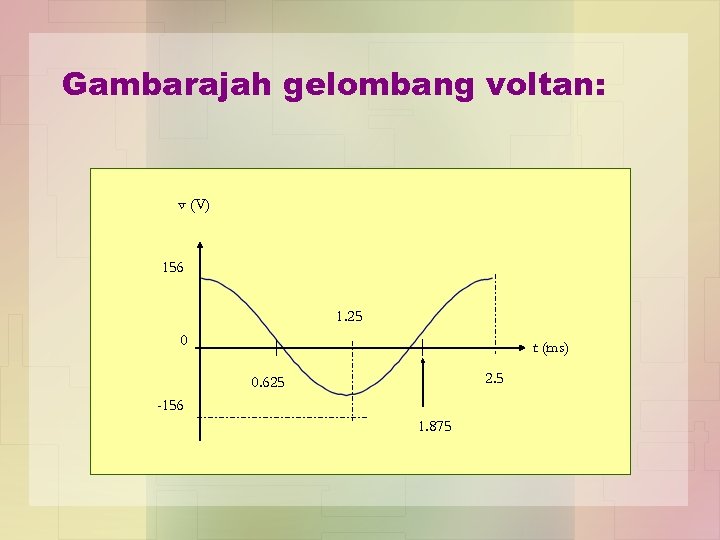Gambarajah gelombang voltan: v (V) 156 1. 25 0 t (ms) 2. 5 0. Gambarajah gelombang voltan: v (V) 156 1. 25 0 t (ms) 2. 5 0. 625 -156 1. 875

INSTANTANEOUS VALUE • The INSTANTANEOUS value of an alternating voltage or current is the INSTANTANEOUS VALUE • The INSTANTANEOUS value of an alternating voltage or current is the value of voltage or current at one particular instant • There actually an infinite number of instantaneous values between zero and the peak value.

AVERAGE VALUE • The AVERAGE value of an alternating current or voltage is the AVERAGE VALUE • The AVERAGE value of an alternating current or voltage is the average of ALL the INSTANTANEOUS values during ONE alternation.

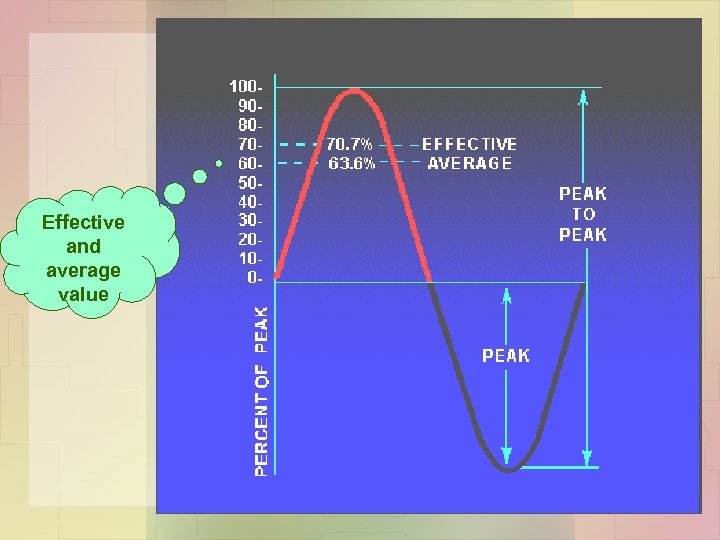Effective and average value Effective and average value

Phase angle (sudut fasa): • Apabila sesuatu gelombang sinus tidak melepasi nilai kosong pada Phase angle (sudut fasa): • Apabila sesuatu gelombang sinus tidak melepasi nilai kosong pada t=0, maka persamaan gelombang tersebut mempunyai sudut fasa yang perlu dipertimbangkan. • Sudut fasa menunjukkan ANJAKAN sesuatu gelombang dari sifar. • Gelombang sinus boleh bermula dari apa-apa nilai seperti berikut. Ia tidak semestinya bermula dari sifar (atau dari nilai puncak bagi fungsi kos).

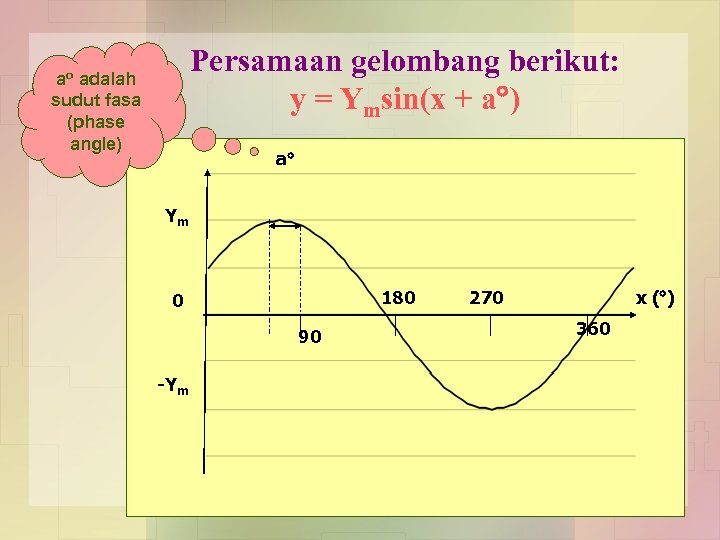Persamaan gelombang berikut: y = Ymsin(x + a ) ao adalah sudut fasa (phase Persamaan gelombang berikut: y = Ymsin(x + a ) ao adalah sudut fasa (phase angle) a Ym 180 0 90 -Ym 270 x ( ) 360

Sine Waves In Phase (sefasa) • When two sine waves are precisely in step Sine Waves In Phase (sefasa) • When two sine waves are precisely in step with one another, they are said to be IN PHASE. To be in phase, the two sine waves must go through their maximum and minimum points at the same time and in the same direction.

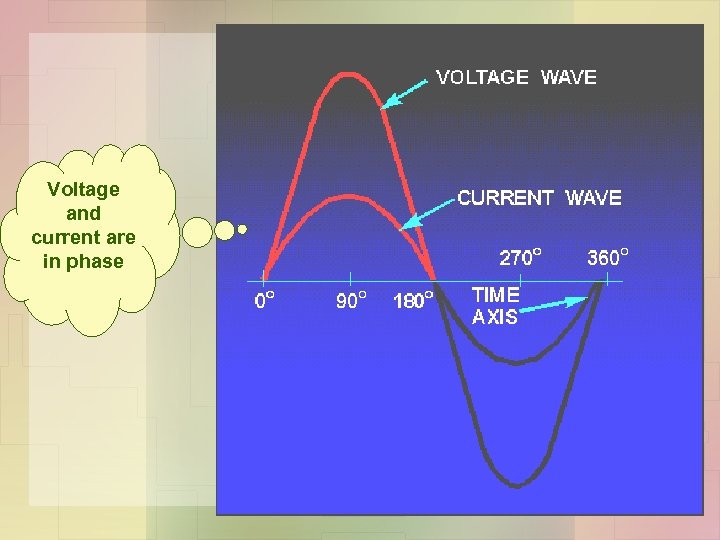Voltage and current are in phase Voltage and current are in phase

Sine Waves Out Of Phase (tidak sefasa) • Voltage wave E 1 which is Sine Waves Out Of Phase (tidak sefasa) • Voltage wave E 1 which is considered to start at 0° (time one). As voltage wave E 1 reaches its positive peak, voltage wave E 2 starts its rise (time two). Since these voltage waves do not go through their maximum and minimum points at the same instant of time, a PHASE DIFFERENCE exists between the two waves. The two waves are said to be OUT OF PHASE.

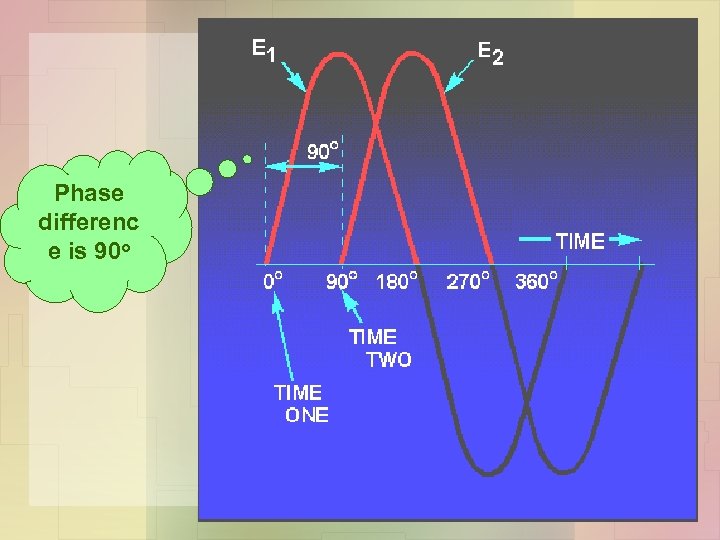Phase differenc e is 90 o Phase differenc e is 90 o

GELOMBANG TIDAK SEFASA • Dua gelombang sinus yang tidak sefasa boleh diwakilkan dengan persamaan: GELOMBANG TIDAK SEFASA • Dua gelombang sinus yang tidak sefasa boleh diwakilkan dengan persamaan: v(t) = Vm kos t ; i(t) = Im kos( t + ) • Arus i(t) MENDAHULU (leading) voltan v(t) dengan sudut . • Dalam sebutan masa, arus mendahului voltan dengan tempoh ( T/360) saat. • Boleh juga disebut voltan MENGEKOR (lagging) arus dengan sudut

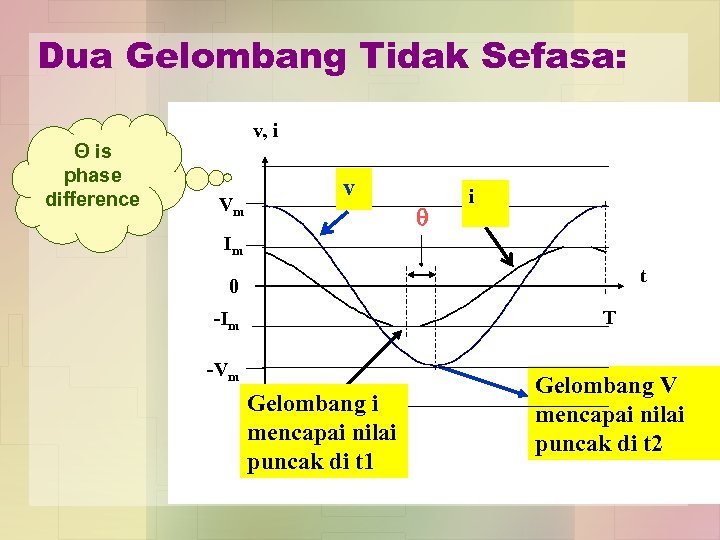Dua Gelombang Tidak Sefasa: Θ is phase difference v, i Vm v i Im Dua Gelombang Tidak Sefasa: Θ is phase difference v, i Vm v i Im t 0 T -Im -Vm Gelombang i mencapai nilai puncak di t 1 Gelombang V mencapai nilai puncak di t 2

CONTOH (4) Lukiskan satu kitar gelombang arus sinus yang diberikan oleh persamaan i(t) = CONTOH (4) Lukiskan satu kitar gelombang arus sinus yang diberikan oleh persamaan i(t) = 70 sin(8000 t + 0. 943 rad) m. A. Tandakan nilai-nilai kritikal.

PENYELESAIAN Bentuk am gelombang arus ialah: i(t) = Im sin( t + ) = PENYELESAIAN Bentuk am gelombang arus ialah: i(t) = Im sin( t + ) = 70 sin(8000 t + 0. 943 rad) Dari persamaan diatas, nilai-nilai kritikal ialah: Im = 70; = 2 f = 8000 ;

f = 4000 Hz = 4 k. Hz; Maka, T = 1/f = 1/4000 f = 4000 Hz = 4 k. Hz; Maka, T = 1/f = 1/4000 = 0. 25 ms; Dan, = 0. 943 rad = 54

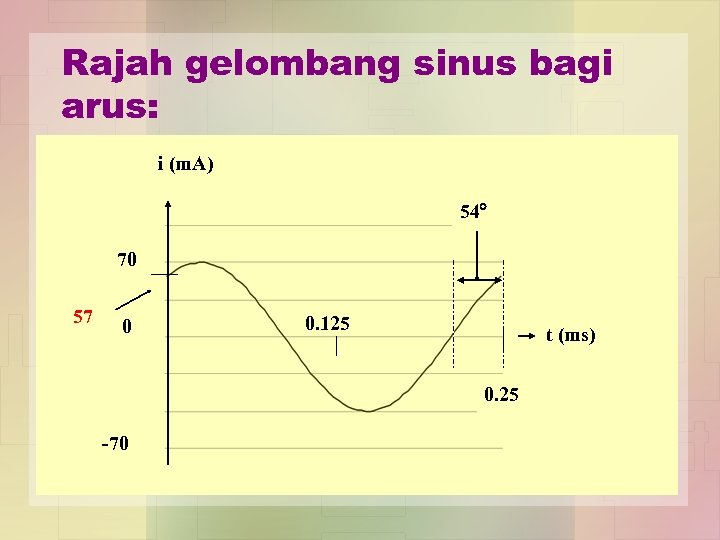Rajah gelombang sinus bagi arus: i (m. A) 54 70 57 0 0. 125 Rajah gelombang sinus bagi arus: i (m. A) 54 70 57 0 0. 125 t (ms) 0. 25 -70

SISTEM SATU FASA • Pengenalan dan ciri-ciri sistem satu fasa • Kebaikan dan keburukan SISTEM SATU FASA • Pengenalan dan ciri-ciri sistem satu fasa • Kebaikan dan keburukan sistem satu fasa • Pengiraan voltan, arus dan kuasa

KEBAIKAN DAN KEBURUKAN SISTEM SATU FASA • Direct current has several disadvantages compared to KEBAIKAN DAN KEBURUKAN SISTEM SATU FASA • Direct current has several disadvantages compared to alternating current. Direct current must be generated at the voltage level required by the load. Alternating current, however, can be generated at a high level and stepped down at the consumer end (through the use of a transformer) to whatever voltage level is required by the load.

• The major advantage that AC electricity has over DC is that AC • The major advantage that AC electricity has over DC is that AC voltages can be transformed to higher or lower voltages. This means that the high voltages used to send electricity over great distances from the power station could be reduced to a safer voltage for use in the house. • This is done by the use of a transformer. This device uses properties of AC electromagnets to change the voltages. • It is easy to convert AC to DC but expensive to convert DC to AC.

SISTEM SATU FASA • Pengenalan dan ciri-ciri sistem satu fasa • Kebaikan dan keburukan SISTEM SATU FASA • Pengenalan dan ciri-ciri sistem satu fasa • Kebaikan dan keburukan sistem satu fasa • Pengiraan voltan, arus dan kuasa

COMPLEX NUMBER 1. POLAR FORM Z= Z n Z : magnitude of Z n COMPLEX NUMBER 1. POLAR FORM Z= Z n Z : magnitude of Z n : angle of Z

2. RECTANGULAR FORM Z = R + j. X § R: real value of 2. RECTANGULAR FORM Z = R + j. X § R: real value of Z § X: imaginary value of Z § j : operator valued √-1

3. EXPONENTIAL FORM Z = rej § r : magnitude § : angle 3. EXPONENTIAL FORM Z = rej § r : magnitude § : angle

RECTANGULAR FORM TO POLAR FORM RECTANGULAR FORM TO POLAR FORM

POLAR FORM TO RECTANGULAR FORM POLAR FORM TO RECTANGULAR FORM

COMPLEX NUMBER ALGEBRA OPERATION • To ADD two number: – Transform to Rectangular • COMPLEX NUMBER ALGEBRA OPERATION • To ADD two number: – Transform to Rectangular • To MULTIPLY two number: – Transform to Polar • To SUBTRACT two number: SUBTRACT – Transform to Polar

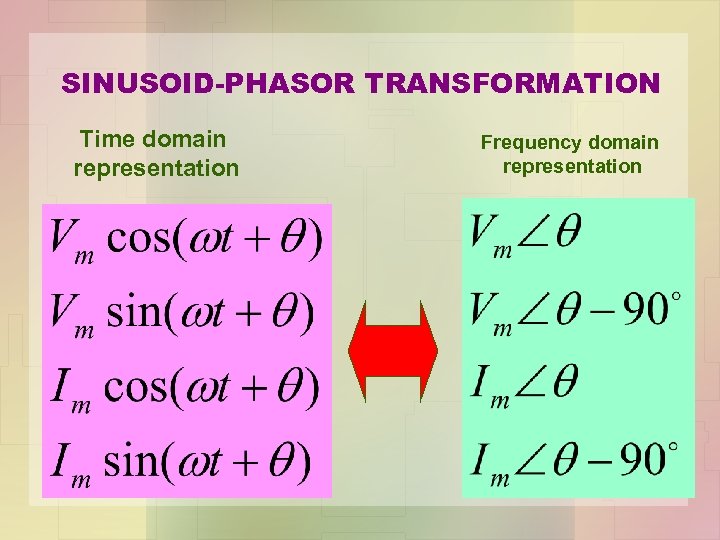SINUSOID-PHASOR TRANSFORMATION Time domain representation Frequency domain representation SINUSOID-PHASOR TRANSFORMATION Time domain representation Frequency domain representation

Ohm’s Law in AC circuit Ohm’s Law in AC circuit

RESISTOR IN AC IN FREQUENCY DOMAIN: RESISTOR IN AC IN FREQUENCY DOMAIN:

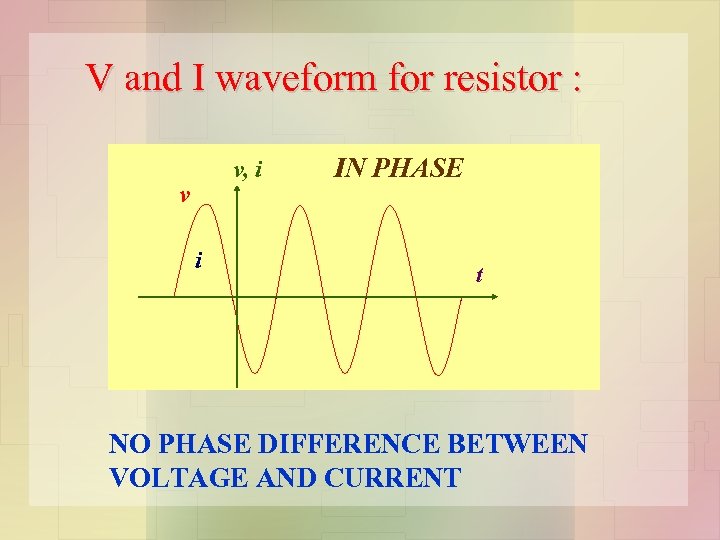V and I waveform for resistor : v, i v i IN PHASE t V and I waveform for resistor : v, i v i IN PHASE t NO PHASE DIFFERENCE BETWEEN VOLTAGE AND CURRENT

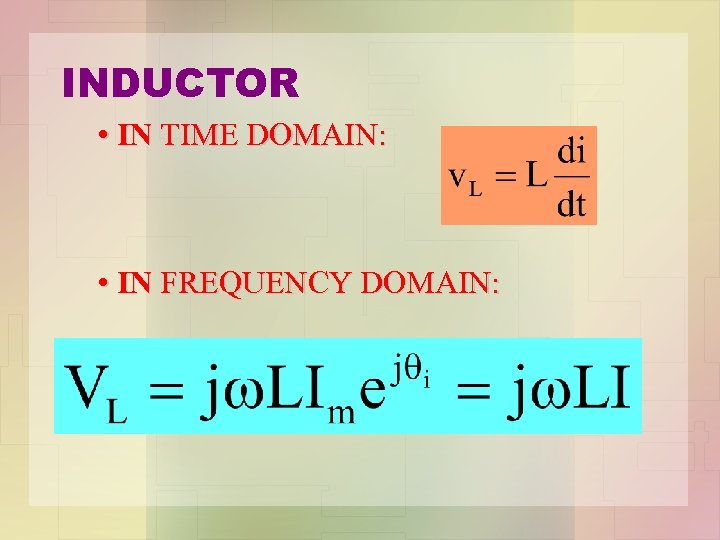INDUCTOR • IN TIME DOMAIN: • IN FREQUENCY DOMAIN: INDUCTOR • IN TIME DOMAIN: • IN FREQUENCY DOMAIN:

GELOMBANG LITAR L v v, i i t 90º ARUS MENGEKOR VOLTAN (ELI) BEZA GELOMBANG LITAR L v v, i i t 90º ARUS MENGEKOR VOLTAN (ELI) BEZA FASA SEBANYAK 90º = (1/4)T = 1/4 f

KAPASITOR • IN TIME DOMAIN: • IN FREQUENCY DOMAIN: KAPASITOR • IN TIME DOMAIN: • IN FREQUENCY DOMAIN:

GELOMBANG LITAR C v, i v i t Arus mendulu voltan sebanyak 90° (ICE) GELOMBANG LITAR C v, i v i t Arus mendulu voltan sebanyak 90° (ICE)

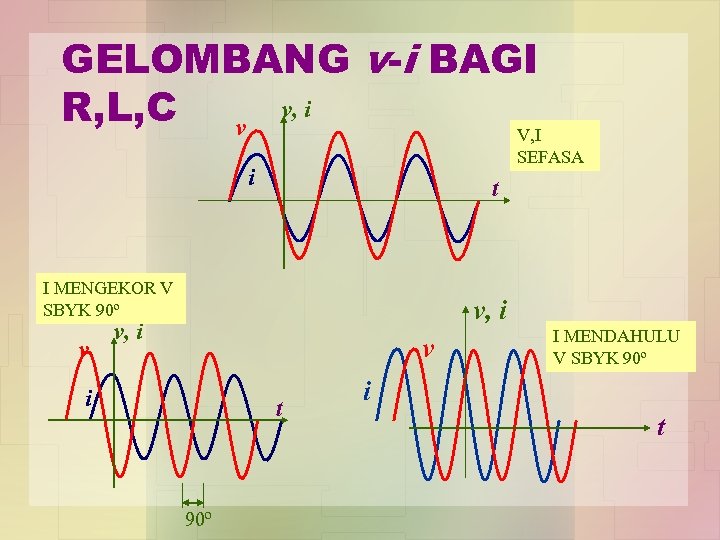GELOMBANG v-i BAGI R, L, C v v, i V, I SEFASA i t GELOMBANG v-i BAGI R, L, C v v, i V, I SEFASA i t I MENGEKOR V SBYK 90º v v, i v i t 90º I MENDAHULU V SBYK 90º i t

Penentuan Mendulu/Mengekor Penentuan Mendulu/Mengekor

ARUS MENGEKOR VOLTAN Dengan menganggap gelombang Arus sbg RUJUKAN: Jika gelombang voltan mpy sudut ARUS MENGEKOR VOLTAN Dengan menganggap gelombang Arus sbg RUJUKAN: Jika gelombang voltan mpy sudut fasa positif Terletak disebelah kiri gelombang arus Gelombang voltan mendulu gelombang arus.

ARUS MENDULU VOLTAN Jika gelombang voltan mpy sudut fasa negatif Terletak disebelah kanan gelombang ARUS MENDULU VOLTAN Jika gelombang voltan mpy sudut fasa negatif Terletak disebelah kanan gelombang arus gelombang voltan mengekor gelombang arus.

AC CIRCUIT ELEMENT REACTANCE AND IMPEDANCE AC CIRCUIT ELEMENT REACTANCE AND IMPEDANCE

REACTANCE All elements in AC circuit (resistor, inductor and capacitor) should have same unit REACTANCE All elements in AC circuit (resistor, inductor and capacitor) should have same unit before you do the analysis.

• Inductor value (in henry) and capasitor value (in farad) must be transform • Inductor value (in henry) and capasitor value (in farad) must be transform into ohms ( ). • Inductance and capacitance value in ohms are known as reactance which is inductive reactance for inductor, and capacitive reactance for capacitor.

• Symbol for inductive reactance is XL and for capacitive reactance is Xc. • Symbol for inductive reactance is XL and for capacitive reactance is Xc. . • Formula to get XL dan Xc: HAFAL!

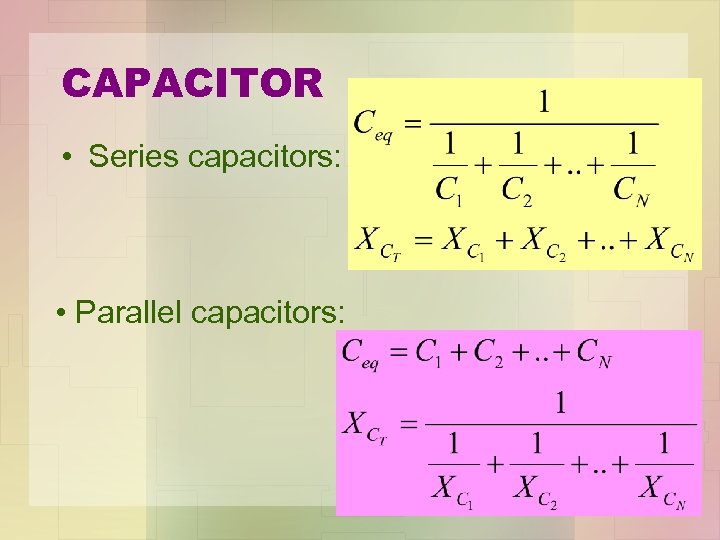CAPACITOR • Series capacitors: • Parallel capacitors: CAPACITOR • Series capacitors: • Parallel capacitors:

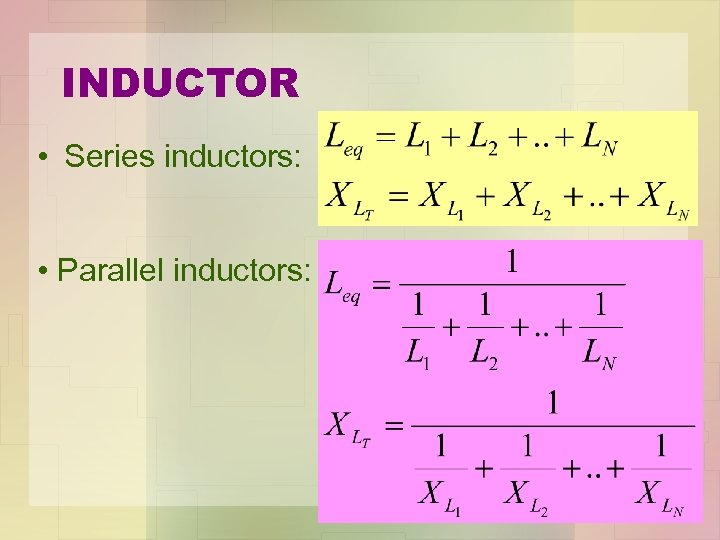INDUCTOR • Series inductors: • Parallel inductors: INDUCTOR • Series inductors: • Parallel inductors:

IMPEDANCE Impedance is a element connecting the resistance, inductive reactance and capacitive reactance in IMPEDANCE Impedance is a element connecting the resistance, inductive reactance and capacitive reactance in time domain.

• Impedance is represent by Z symbol: (ohms) • is angle between voltage • Impedance is represent by Z symbol: (ohms) • is angle between voltage and current • Impedance is complex number because of magnitude and angle

• Resistance impedance, ZR: • Resistance impedance, ZR:

• Inductive impedance, ZL • Inductive impedance, ZL

• Capacitive impedance, Zc • Capacitive impedance, Zc

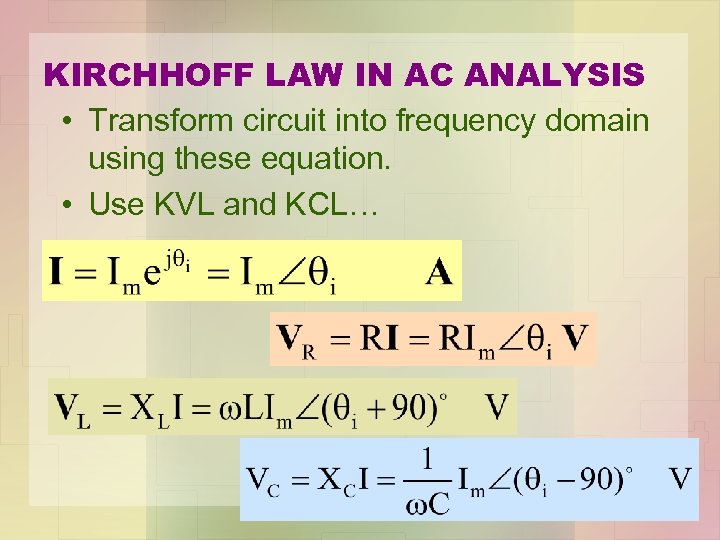KIRCHHOFF LAW IN AC ANALYSIS • Transform circuit into frequency domain using these equation. KIRCHHOFF LAW IN AC ANALYSIS • Transform circuit into frequency domain using these equation. • Use KVL and KCL…

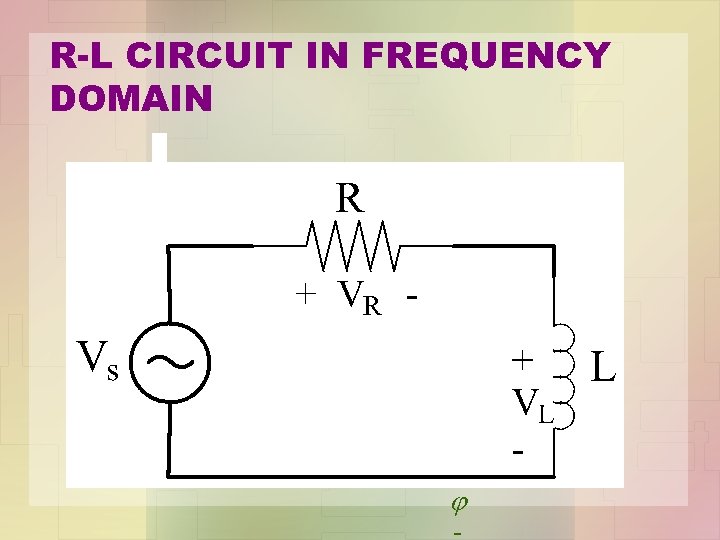R-L CIRCUIT IN FREQUENCY DOMAIN +R j VI VL = L V R V R-L CIRCUIT IN FREQUENCY DOMAIN +R j VI VL = L V R V m

CONTOH (1) : LITAR RL Given Vs = 40 cos (2000 t - 60º). CONTOH (1) : LITAR RL Given Vs = 40 cos (2000 t - 60º). Find, a) Phasor voltage across R; b) Phasor voltage across L; c) Current, i(t) expression

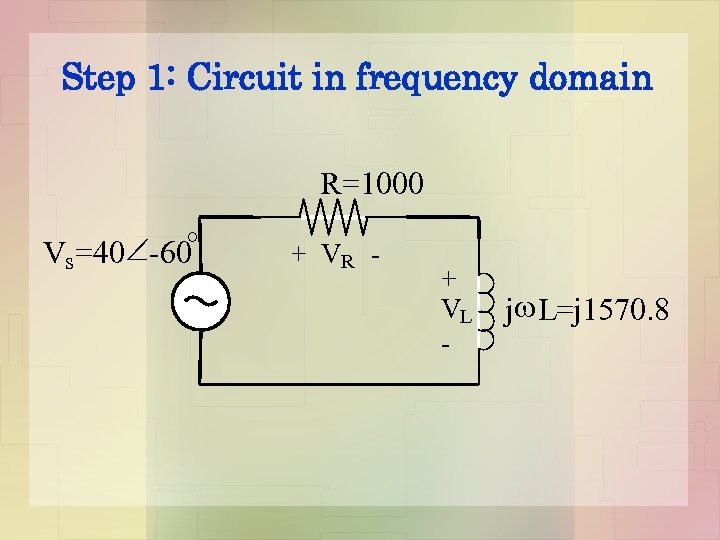Step 1: Circuit in frequency domain R=1000 Vs=40 -60° + VR - + VL Step 1: Circuit in frequency domain R=1000 Vs=40 -60° + VR - + VL - j L=j 1570. 8

Step 2: Find circuit impedance Step 2: Find circuit impedance

Step 3: Calculate current Step 3: Calculate current

Phasor current is; Phasor current is;

(a) Phasor voltage across R, (a) Phasor voltage across R,

(b) Phasor voltage across L, (b) Phasor voltage across L,

(c) Current, i(t) expression: » » Transform I in time domain (c) Current, i(t) expression: » » Transform I in time domain

CONTOH (2) : LITAR RC Given VC = 60 cos(1000 t - 33º). Find, CONTOH (2) : LITAR RC Given VC = 60 cos(1000 t - 33º). Find, a) Phasor current, I b) Phasor voltage across R c) Voltage source, vs(t).

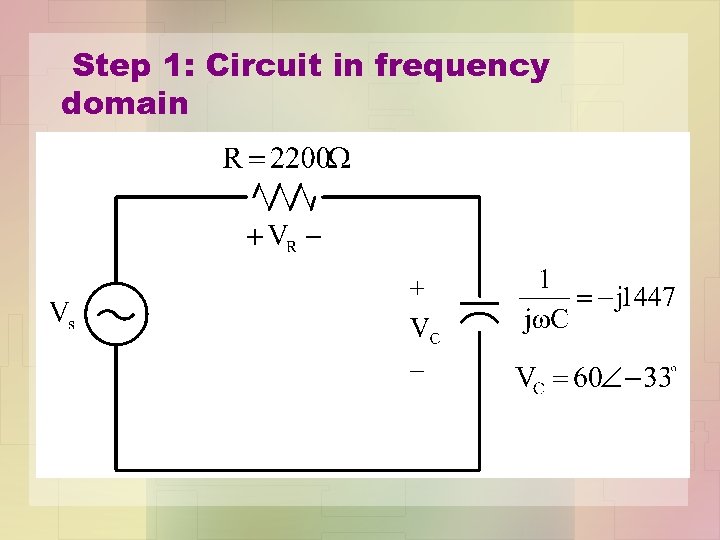Step 1: Circuit in frequency domain Step 1: Circuit in frequency domain

Step 2: Circuit impedance (Z) Step 2: Circuit impedance (Z)

Step 3: Find I, VR, VS (a) Phasor current; (b) Phasor voltage across R; Step 3: Find I, VR, VS (a) Phasor current; (b) Phasor voltage across R;

(c) Source phasor voltage; Transform V into time domain; (c) Source phasor voltage; Transform V into time domain;

IMPEDANCE TRIANGLE IMPEDANCE TRIANGLE

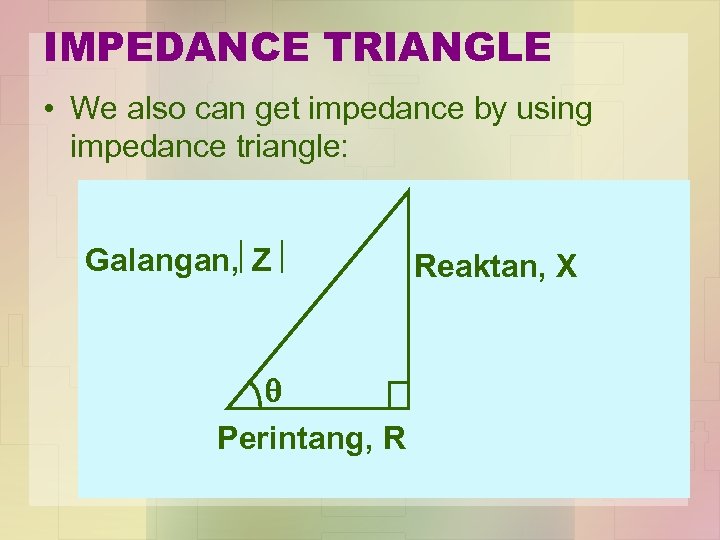IMPEDANCE TRIANGLE • We also can get impedance by using impedance triangle: Galangan, Z IMPEDANCE TRIANGLE • We also can get impedance by using impedance triangle: Galangan, Z Perintang, R Reaktan, X

• Dari segitiga galangan; • Ini bermakna, dengan mengetahui Galangan (Z), kita boleh • Dari segitiga galangan; • Ini bermakna, dengan mengetahui Galangan (Z), kita boleh juga mengetahui nilai perintang (R) dan Reaktan (X).

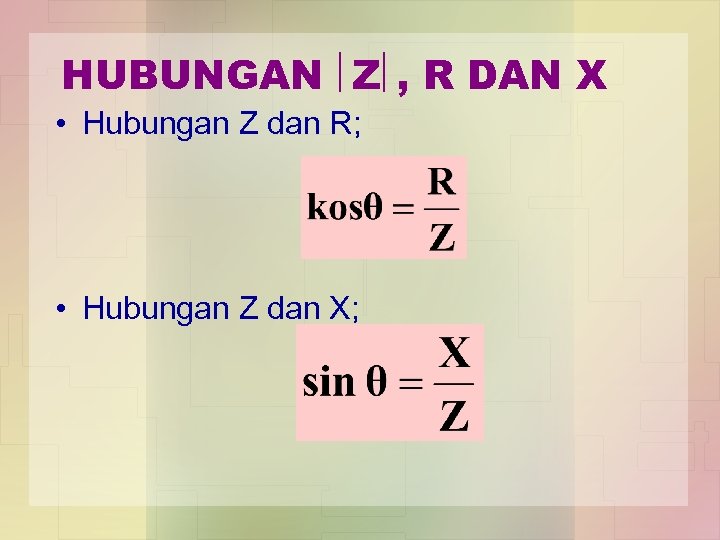HUBUNGAN Z , R DAN X • Hubungan Z dan R; • Hubungan Z HUBUNGAN Z , R DAN X • Hubungan Z dan R; • Hubungan Z dan X;

AC Power Calculation AC Power Calculation

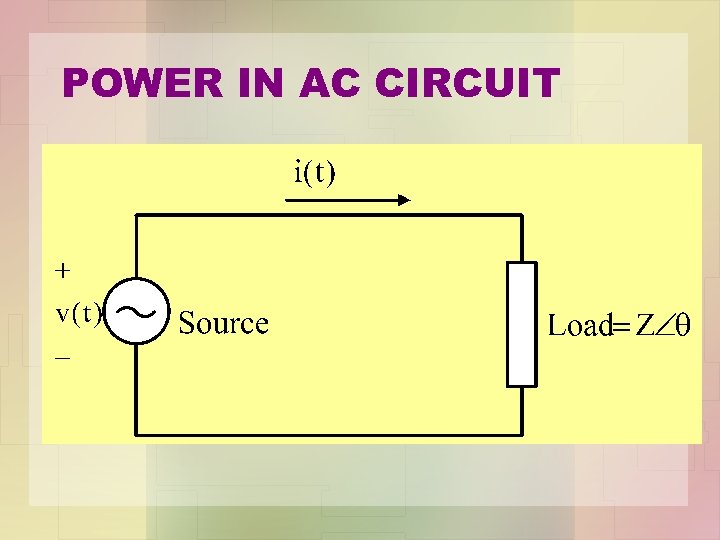POWER IN AC CIRCUIT POWER IN AC CIRCUIT

INSTANTENAOUS POWER (KUASA SEKETIKA) • Kuasa seketika yg diserap oleh setiap peranti elektrik adalah INSTANTENAOUS POWER (KUASA SEKETIKA) • Kuasa seketika yg diserap oleh setiap peranti elektrik adalah hasil darab Voltan seketika yg merintanginya dan Arus seketika yang melaluinya.

RMS VALUE • Semua nilai Voltan dan Arus dalam pengiraan kuasa adalah menggunakan nilai RMS VALUE • Semua nilai Voltan dan Arus dalam pengiraan kuasa adalah menggunakan nilai RMS (root mean square). Iaitu: • Dimana, Vm dan Im adalah Nilai Puncak (peak) bagi voltan dan arus.

1. AVERAGE POWER (KUASA PURATA) • Kuasa purata atau kuasa sebenar ditakrifkan sebagai: • 1. AVERAGE POWER (KUASA PURATA) • Kuasa purata atau kuasa sebenar ditakrifkan sebagai: • Unit bagi kuasa purata ialah Watt.

• Kuasa purata pada Perintang boleh juga diwakili oleh persamaan berikut: • Kita • Kuasa purata pada Perintang boleh juga diwakili oleh persamaan berikut: • Kita tahu V=IR, maka kuasa purata turut diwakili oleh:

• Kuasa purata ialah kuasa berguna yg. disebabkan oleh elemen Perintang. • Dengan • Kuasa purata ialah kuasa berguna yg. disebabkan oleh elemen Perintang. • Dengan itu, kuasa purata bagi beban reaktif (L atau C) adalah Kosong. • ialah Sudut antara Voltan dan Arus, ATAU dikenali juga sebagai Sudut Galangan, Z.

Nilai diperolehi seperti berikut: Nilai diperolehi seperti berikut:

CONTOH (1) Voltan sinus mempunyai amplitud maksimum 625 Volt dikenakan pada terminal yg mempunyai CONTOH (1) Voltan sinus mempunyai amplitud maksimum 625 Volt dikenakan pada terminal yg mempunyai Perintang 50. Dapatkan kuasa purata yang dihantar kepada perintang tersebut.

PENYELESAIAN • Nilai rms: • Kuasa purata bagi perintang diperolehi: PENYELESAIAN • Nilai rms: • Kuasa purata bagi perintang diperolehi:

2. REACTIVE POWER (KUASA REAKTIF) • Kuasa Reaktif ditakrifkan sebagai: 2. REACTIVE POWER (KUASA REAKTIF) • Kuasa Reaktif ditakrifkan sebagai:

• Kuasa reaktif juga merupakan kuasa yg disimpan oleh elemen reaktif iaitu L • Kuasa reaktif juga merupakan kuasa yg disimpan oleh elemen reaktif iaitu L atau C. • Maka, kuasa reaktif boleh juga dicari dengan:

CONTOH (2) Diberi v= 100 kos ( t + 15º) dan i= 4 sin CONTOH (2) Diberi v= 100 kos ( t + 15º) dan i= 4 sin ( t - 15º), Pada terminal rangkaian, dapatkan: (a)Kuasa purata (b)Kuasa reaktif i + v - Rangkaian

PENYELESAIAN • Tukarkan persamaan arus, i dalam bentuk kos: i= 4 kos ( t PENYELESAIAN • Tukarkan persamaan arus, i dalam bentuk kos: i= 4 kos ( t - 105º) • Dari persamaan Kuasa Purata: • Maka,

• Dari pers. Kuasa reaktif: • Maka, • Dari pers. Kuasa reaktif: • Maka,

• Nilai kuasa purata, P= -100 W: Bermaksud kuasa purata telah dihantar balik • Nilai kuasa purata, P= -100 W: Bermaksud kuasa purata telah dihantar balik dari beban kepada terminal bekalan. • Nilai kuasa reaktif, Q=173. 21 Var: Bermaksud kuasa reaktif telah diserap oleh beban.

AC POWER FORMULA • AC power calculation can be done by using these formula: AC POWER FORMULA • AC power calculation can be done by using these formula: