Single Crystal Structure Determination of Organic and Organometallic

Single Crystal Structure Determination of Organic and Organometallic Compounds A. L. (Ton) Spek National Single Crystal Service Facility Utrecht University Amsterdam, 23 -10 -2007

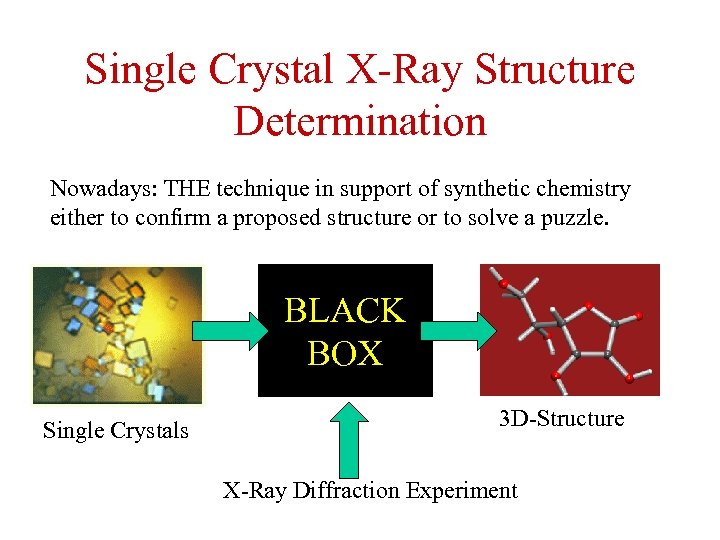Single Crystal X-Ray Structure Determination Nowadays: THE technique in support of synthetic chemistry either to confirm a proposed structure or to solve a puzzle. BLACK BOX Single Crystals 3 D-Structure X-Ray Diffraction Experiment

Some History • The first X-ray structure determination was carried out around 1913 (Bragg). • In the sixties, 40 years ago, a small molecule crystal structure determination still took in the order of half a year. • Main problems were the time consuming data collection, the solution of the ‘Phase Problem’ and the scarce and slow university main frame computing facilities. • We received in the late 70 th an interesting request from a synthetic chemist interested in the 3 D structure of a new compound: ‘. . Can you inject this sample in your diffractometer. . ’, a request that looked naïve at the time. • In hindsight he was visionary, since …

Announced Aug 2007: Tabletop ‘Black Box’ – Smart X 2 S Crystal Structure ?

Current Status • Data collection and evaluation procedures have now evolved to a level that a subset of the routine samples can indeed be analyzed automatically in a matter of hours. • The problem is that many real world samples still turn out to be non-routine. • Thus still a working knowledge is needed of what is in the box … in order to get a reliable structure.

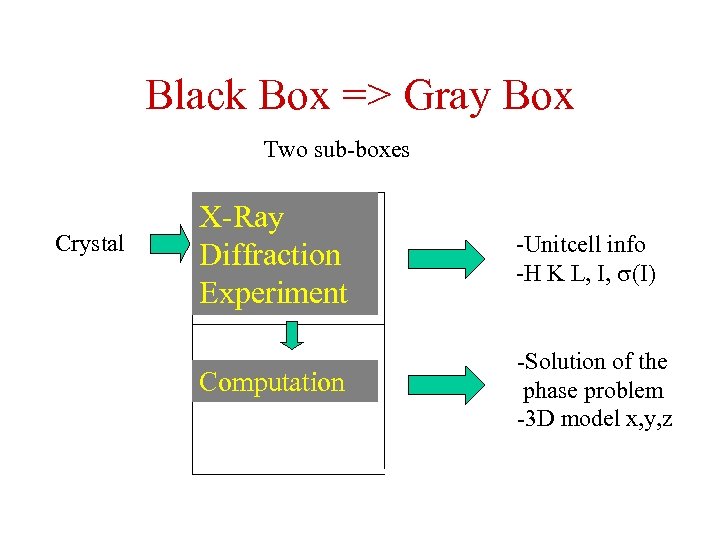Black Box => Gray Box Two sub-boxes Crystal X-Ray Diffraction Experiment -Unitcell info -H K L, I, (I) Computation -Solution of the phase problem -3 D model x, y, z

X-Ray Diffraction Experiment X-Ray Sources • Sealed Tube (Cu. Ka, Mo. Ka) 1 -3 k. W • Rotating Anode (Cu. Ka, Mo. Ka) ~ 10 k. W • Rotating Anode + Focussing Mirrors • New: Microsource ~30 W Low Temperature Unit for the best data

X-Ray Diffraction Experiment Reflection Registration. Techniques • 2 D-X-Ray Film (Weissenberg Camera etc. ) • 1 D-Point Detector (Scientilation counter – CAD 4 Automation • 2 D-Image Plate • CCD 2 D Detector (Kappa. CCD, APEX) • Future? Real time 2 D low noise, shutterless detectors

X-Ray source, Goniometer & Serial Detector

LNT CCD - Detector X-ray Crystal Goniometer X-ray source, goniometer + crystal, N 2 -cooling and CCD Detector

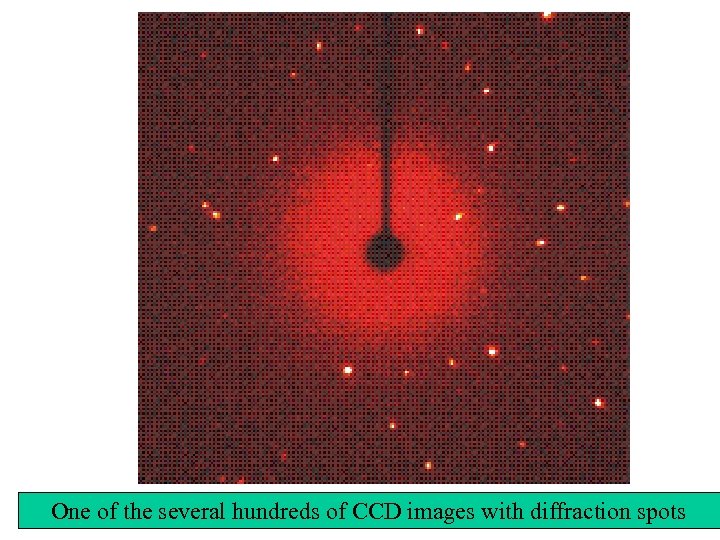One of the several hundreds of CCD images with diffraction spots

Data Collection • Diffraction Condition (determines the position of the diffracted beams on the detector): 2 dhkl sin(Q) = n l (Bragg Equation) • Result: - Cell Dimensions, a, b, c, a, b, g - Reflection intensities by planes (hkl) in the crystal: I(hkl) (many thousands)

Computation • • Data Reduction to hkl I and (I) Correction for absorption effects Determination of the Space Group Solution of the Phase Problem Abstraction of a Parameter Model from 3 D-density map Refinement of the Structural Model Analysis of the geometry, intermolecular interactions Structure Validation

Data Reduction • Integration and scaling of the diffraction intensities • E. g. with programs (Generally comes with the hardware) DENZO, EVAL-CCD, SAINT

Correction for Absorption • Numerical correction based on the description of the crystal in terms of its bounding faces. • Correction based on Phi-scans (Serial Det. ) • Fitted ‘Absorption Surface’ based on multiple measured reflections with different setting angles (SADABS, TWINABS, MULABS etc. )

Determination of the Space Group Based on: • Cell Dimensions • Laue Symmetry • Intensity Statistics (Centro/Non-Centro) • Systematic Extinctions • Space Group Frequency in the CSD Note: Not always a unique proposal

Structure Determination • Experiment Ihkl |Fhkl| = Sqrt(Ihkl) • Needed for 3 D structure (approximate) Phases: fhkl |Fhkl| + fhkl = Fhkl 3 D-Fourier Synthesis r(x, y, z) = [ Shkl Fhkl exp{-2 i(hx + ky + lz)}] / V x, y, z are fractional coordinates (range 0 1) Example next slide

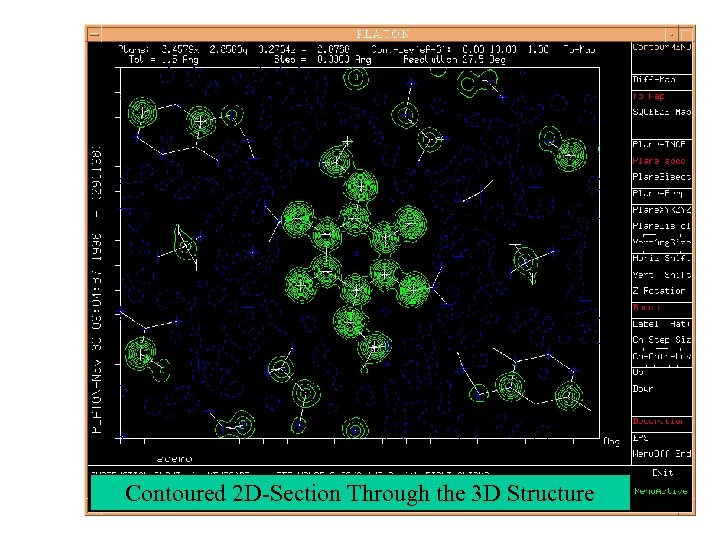Contoured 2 D-Section Through the 3 D Structure

Solution of the Phase Problem • Direct Methods e. g. SHELXS, SHELXD, SIR, CRUNCH • Patterson Methods DIRDIF • Fourier Difference Maps (Structure Completion) • New: Charge Flipping

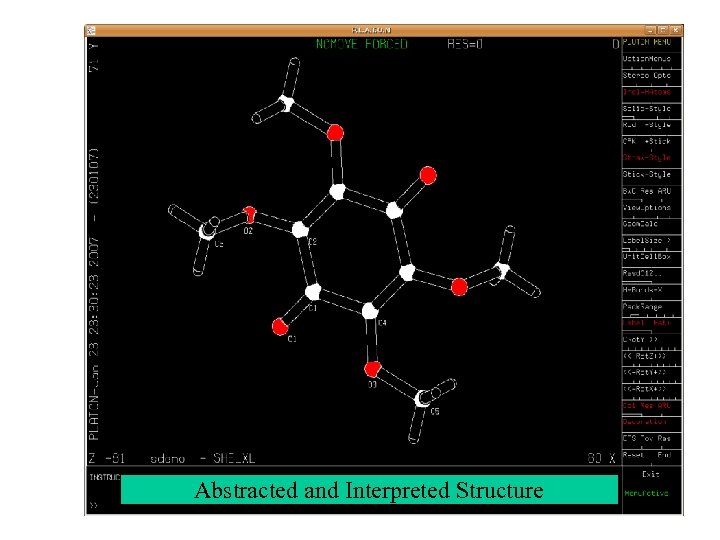Abstracted and Interpreted Structure

3 D Parameter Model • Extract the 3 D Coordinates (x, y, z) of the atoms. • Assign Atom Types (Scattering type C, O etc. ) • Assign Additional Parameters to Model the Thermal Motion (T) of the Atoms. • Other Parameters: Extinction, Twinning, Flack x • Model: Fhkl = Sj=1, n fj T exp{2 i(hx + ky + lz)} • Non-linear Least-squares Parameter Refinement until Convergence. • Minimize: Shkl w [(Fhklobs)2 – (Fhklcalc)2]2 • Agreement Factor: R = S |Fobs – Fcalc| / S|Fobs|

Refinement of the Structural Model Refinement Steps (Programs SHELXL, Crystals, XTAL etc) 1. Refine positional parameters + isotropic U 2. Refine positional + anisotropic parameters 3. Introduce H-atoms 4. Refine H-atoms with x, y, z, U(iso) or riding on their carrier atoms 5. Refine weighting scheme 6. ORTEP presentation

Analysis of the Geometry and Intermolecular Interactions Programs: PLATON, PARST etc • Bond distances, angles, torsion angles, ring (puckering) geometry etc. • Intermolecular Contacts Hydrogen Bonds (O-H. . O, N-H. . O, O-H. . )

Structure Validation • • • Refinement results in CIF File format. Final Fobs/Fcalc data in FCF File Format IUCr CHECKCIF tool PLATON Validation Tool Check in Cambridge Crystallographic Database for similar structures.

Technical Issues and Problems • • • Poor crystal quality (e. g. fine needle bundles) Determination of the correct Space Group Symmetry Pseudo-Symmetry Absolute Structure of light atom structures Twinning Positional and substitutional disorder of part (or even the whole) molecule • Disordered Solvent • Incommensurate structures • Diffuse scattering, streaks, diffuse layers

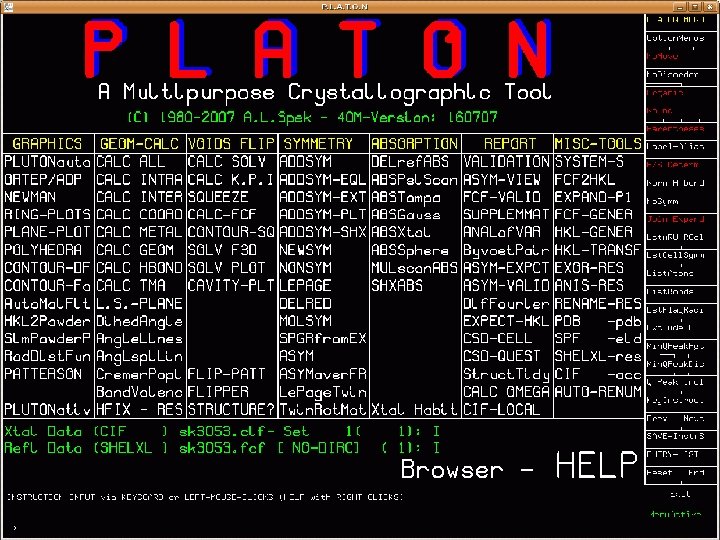
Tools offered by PLATON • The program PLATON offers multiple tools that can be used to analyse and solve problems encountered in a single crystal structure determination • Next slide Main Feature Menu PLATON

Selected Tools • ADDSYM – Detection and Handling of Missed (Pseudo)Symmetry • Twin. Rot. Mat – Detection of Twinning • SOLV – Report of Solvent Accessible Voids • SQUEEZE – Handling of Disordered Solvents in Least Squares Refinement (Easy to use Alternative for Clever Disorder Modelling) • Bijvoet. Pair – Post-refinement Absolute Structure Determination (Alternative for Flack x) • VALIDATION – PART of IUCr CHECKCIF

ADDSYM • About 1% of the 2006 & 2007 entries in the CSD need a change of space group. • Often, a structure solves only in a space group with lower symmetry than the correct space group. The structure should subsequently be checked for higher symmetry. • Next slides: Recent examples of missed symmetry

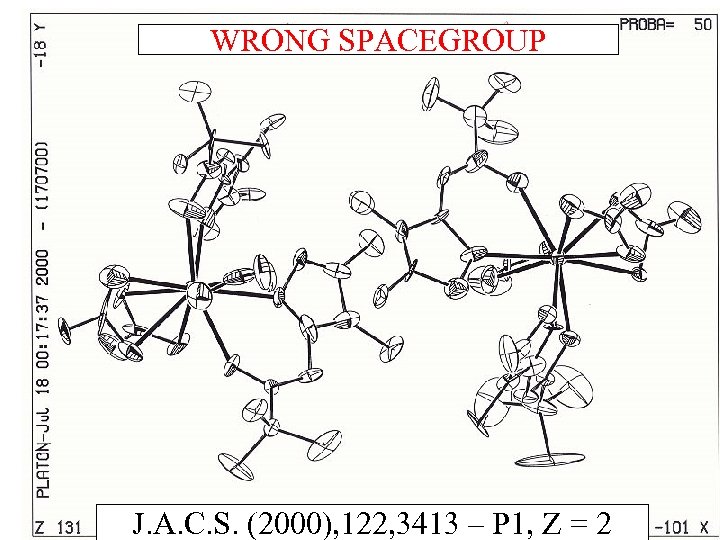WRONG SPACEGROUP J. A. C. S. (2000), 122, 3413 – P 1, Z = 2

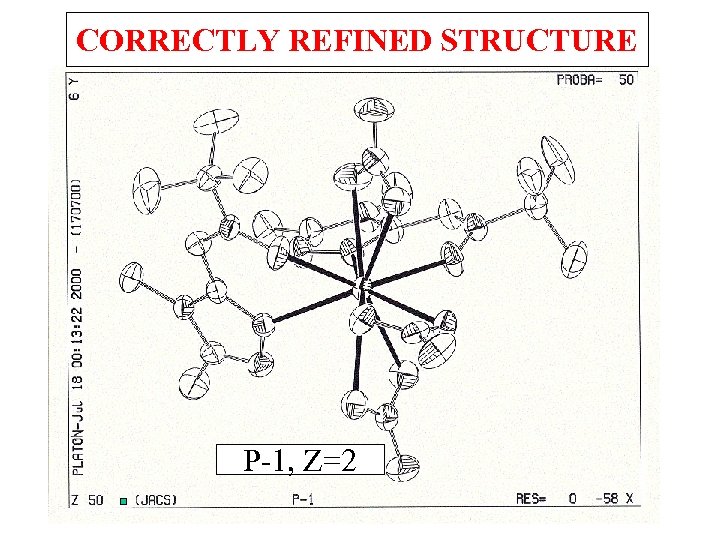CORRECTLY REFINED STRUCTURE P-1, Z=2

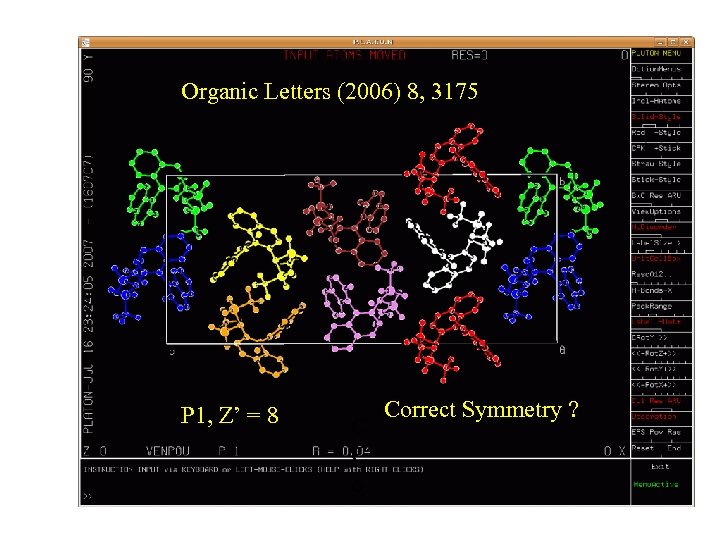Organic Letters (2006) 8, 3175 P 1, Z’ = 8 C C o Correct Symmetry ?

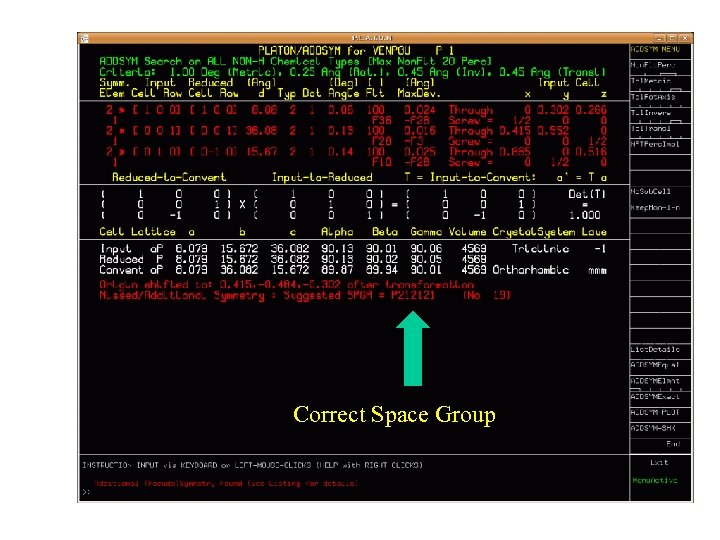Correct Space Group

After Transformation to P 212121, Z’ = 2

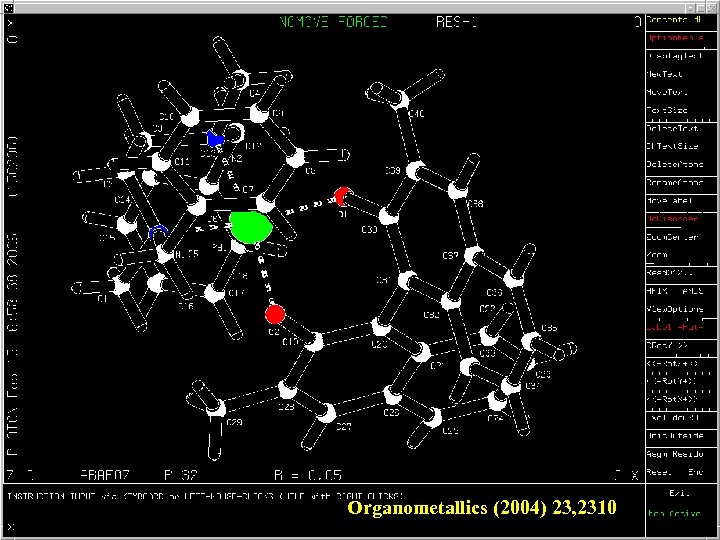Organometallics (2004) 23, 2310

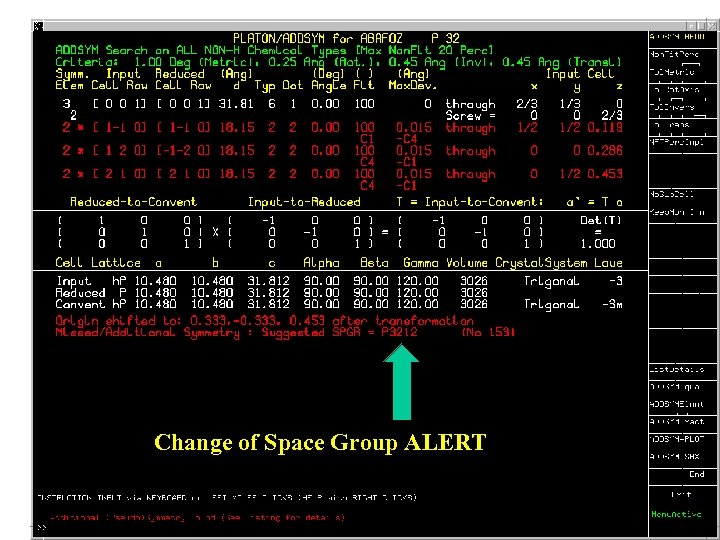Change of Space Group ALERT

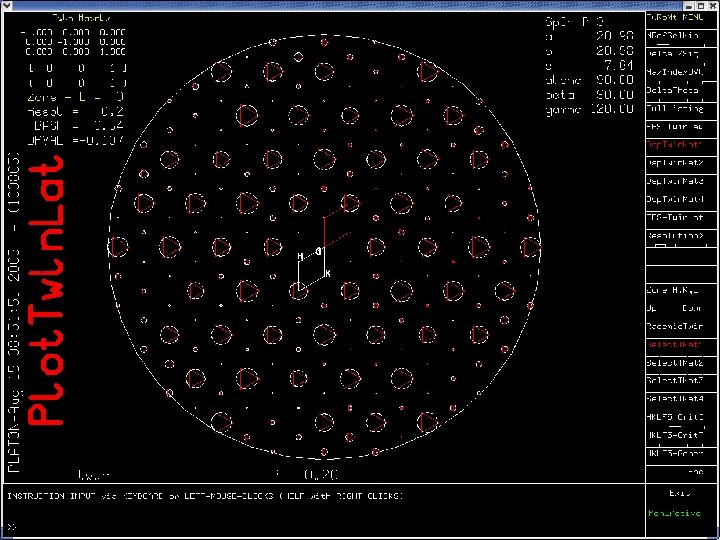
(Pseudo)Merohedral Twinning • Options to handle twinning in L. S. refinement available in SHELXL, CRYSTALS etc. • Problem: Determination of the Twin Law that is in effect. • Partial solution: coset decomposition, try all possibilities (I. e. all symmetry operations of the lattice but not of the structure) • ROTAX (S. Parson et al. (2002) J. Appl. Cryst. , 35, 168. (Based on the analysis of poorly fitting reflections of the type F(obs) >> F(calc) ) • Twin. Rot. Mat Automatic Twinning Analysis as implemented in PLATON (Based on a similar analysis but implemented differently)

Twin. Rot. Mat Example • Originally published as disordered in P 3. • Solution and Refinement in the trigonal space group P-3 R= 20%. • Run PLATON/Twin. Rot. Mat on CIF/FCF • Result: Twin law with an the estimate of the twinning fraction and the estimated drop in R-value • Example of a Merohedral Twin

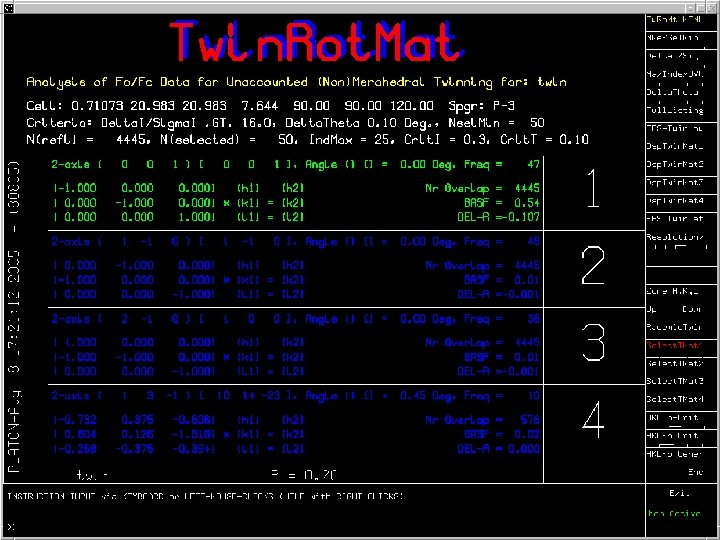
Ideas behind the Algorithm • Reflections effected by twinning show-up in the least-squares refinement with F(obs) >> F(calc) • Overlapping reflections necessarily have the same Theta value within a tolerance. • Generate a list of implied possible twin axes based on the above observations. • Test each proposed twin law for its effect on the R -value.

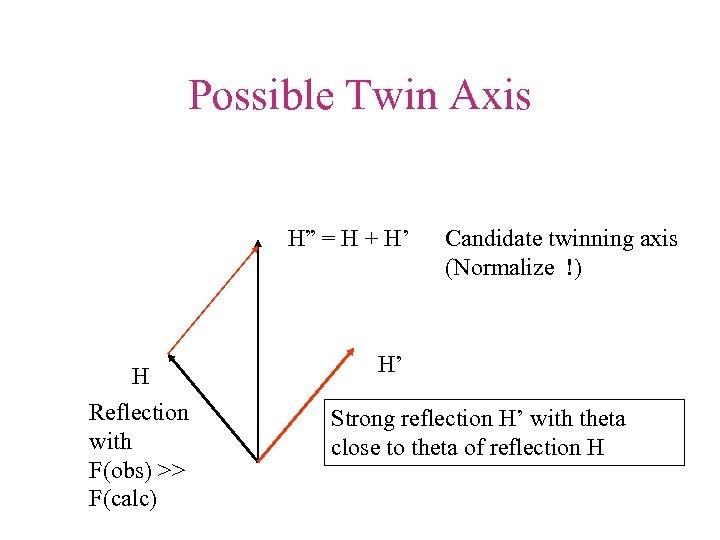Possible Twin Axis H” = H + H’ H Reflection with F(obs) >> F(calc) Candidate twinning axis (Normalize !) H’ Strong reflection H’ with theta close to theta of reflection H

Solvent Accessible Voids • A typical crystal structure has only in the order of 65% of the available space filled. • The remainder volume is in voids (cusps) in-between atoms (too small to accommodate an H-atom) • Solvent accessible voids can be defined as regions in the structure that can accommodate at least a sphere with radius 1. 2 Angstrom without intersecting with any of the van der Waals spheres assigned to each atom in the structure. • Next Slide: Void Algorithm: Cartoon Style

DEFINE SOLVENT ACCESSIBLE VOID STEP #1 – EXCLUDE VOLUME INSIDE THE VAN DER WAALS SPHERE

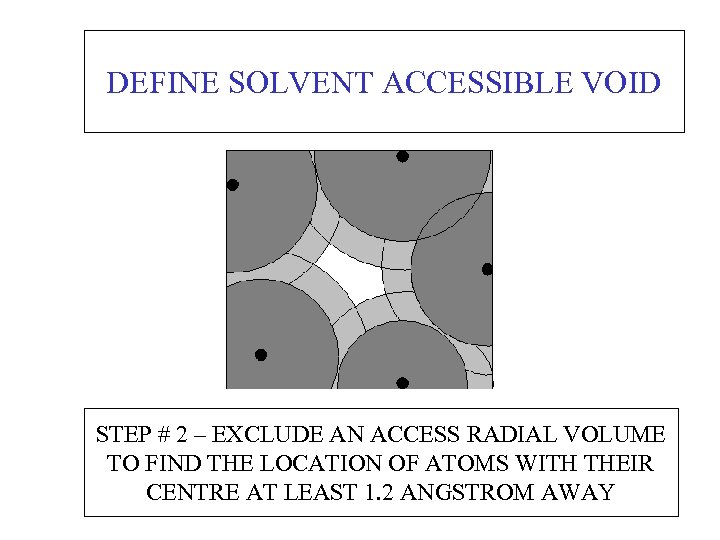DEFINE SOLVENT ACCESSIBLE VOID STEP # 2 – EXCLUDE AN ACCESS RADIAL VOLUME TO FIND THE LOCATION OF ATOMS WITH THEIR CENTRE AT LEAST 1. 2 ANGSTROM AWAY

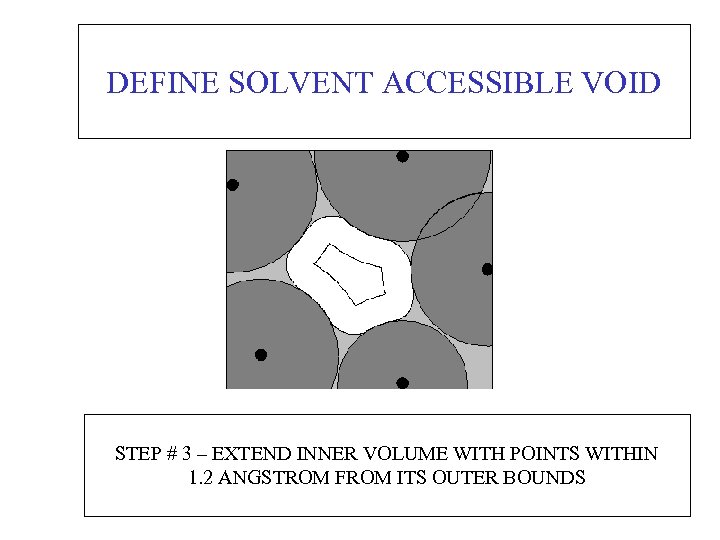DEFINE SOLVENT ACCESSIBLE VOID STEP # 3 – EXTEND INNER VOLUME WITH POINTS WITHIN 1. 2 ANGSTROM FROM ITS OUTER BOUNDS

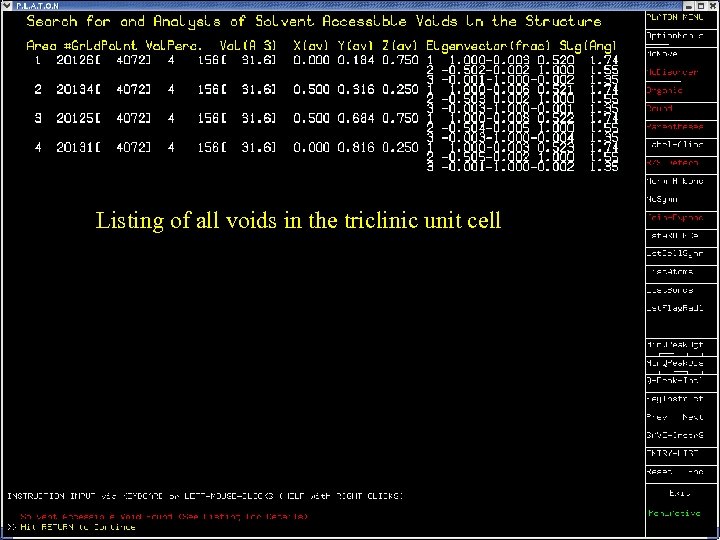Listing of all voids in the triclinic unit cell Cg

VOID APPLICATIONS • Calculation of Kitaigorodskii Packing Index • As part of the SQUEEZE routine to handle the contribution of disordered solvents in crystal structure refinement • Determination of the available space in solid state reactions (Ohashi) • Determination of pore volumes, pore shapes and migration paths in microporous crystals

SQUEEZE • Takes the contribution of disordered solvents to the calculated structure factors into account by back-Fourier transformation of density found in the ‘solvent accessible volume’ outside the ordered part of the structure (iterated). • Filter: Input shelxl. res & shelxl. hkl Output: ‘solvent free’ shelxl. hkl • Refine with SHELXL or Crystals • Note: SHELXL lacks option for fixed contribution to Structure Factor Calculation.

SQUEEZE Algorithm 1. 2. 3. 4. 5. Calculate difference map (FFT) Use the VOID-map as a mask on the FFT-map to set all density outside the VOID’s to zero. FFT-1 this masked Difference map -> contribution of the disordered solvent to the structure factors Calculate an improved difference map with F(obs) phases based on F(calc) including the recovered solvent contribution and F(calc) without the solvent contribution. Recycle to 2 until convergence.

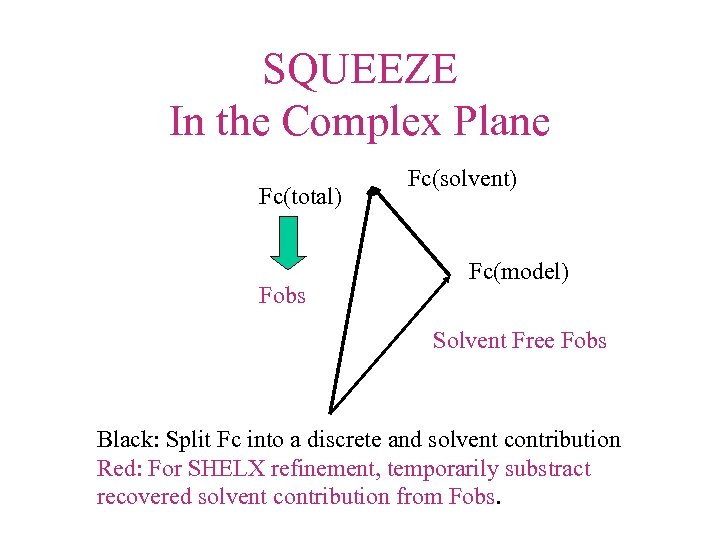SQUEEZE In the Complex Plane Fc(total) Fobs Fc(solvent) Fc(model) Solvent Free Fobs Black: Split Fc into a discrete and solvent contribution Red: For SHELX refinement, temporarily substract recovered solvent contribution from Fobs.

Comment • The Void-map can also be used to count the number of electrons in the masked volume. • A complete dataset is required for this feature. • Ideally, the solvent contribution is taken into account as a fixed contribution in the Structure Factor calculation (CRYSTALS) otherwise it is subtracted temporarily from Fobs 2 (SHELXL) and re-instated afterwards with info saved beyond column 80 for the final Fo/Fc list.

Publication Note • Always give the details of the use of SQUEEZE in the comment section • Append the small CIF file produced by PLATON to the main CIF • Use essentially complete data sets with sufficient resolution only. • Make sure that there is no unresolved charge balance problem.

Absolute Structure Determination Complex Scattering Factors • Scattering factor: f = f 0 + f ’ + if ’’ Where: f 0 = a function of diffraction angle Q and equal to the number of electrons in the atom at Q = 0. f ‘and f ’’ atom type and l dependent i = sqrt(-1) • Note: A phase shift is often represented mathematically as a complex number.

Breakdown of Friedels Law • It can be derived from the expression for the calculated structure factor that for noncentrosymmetric crystal structures: |Fhkl| not necessarily equal to |F-h-k-l| for f “ > 0, thus breaking the earlier assumed Friedel Law: |Fhkl| = |F-h-k-l| (The Friedel Law still holds for centro-symmetric structures containing racemic mixtures of chiral compounds).

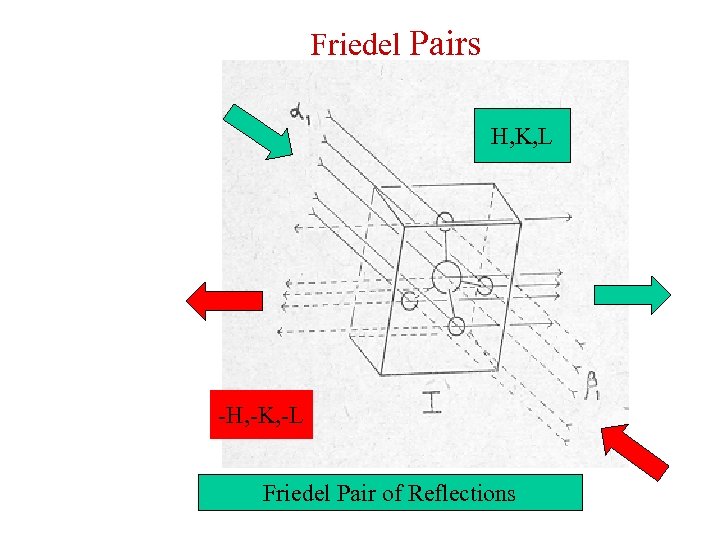Friedel Pairs H, K, L -H, -K, -L Friedel Pair of Reflections

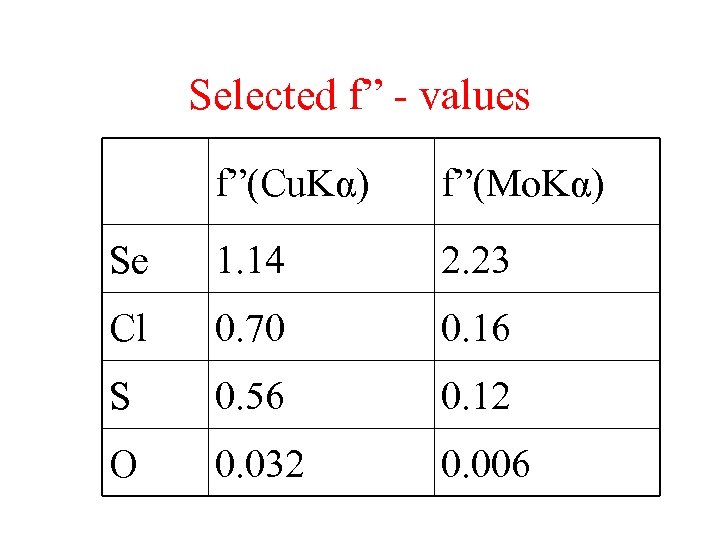Selected f” - values f”(Cu. Kα) f”(Mo. Kα) Se 1. 14 2. 23 Cl 0. 70 0. 16 S 0. 56 0. 12 O 0. 032 0. 006

Flack Parameter • The current official method to establish the absolute configuration of a chiral molecule calls for the determination of the Flack x parameter. Flack, H. D. (1983). Acta Cryst. A 39, 876 -881. • Twinning Model (mixture model and image): Ihklcalc = (1 – x) |Fhkl|2 + x |F-h-k-l|2 • Result of the least-squares refinement: x(u) Where x has physically a value between 0 and 1 and u the standard uncertainty (‘esd’)

Interpretation of the Flack x • H. D. Flack & G. Bernardinelli (2000) J. Appl. Cryst. 33, 1143 -1148. • For a statistically valid determination of the absolute structure: u should be < 0. 04 and |x| < 2 u • For a compound with known enantiopurity: u should be < 0. 1 and |x| < 2 u

Post-Refinement Absolute Structure Determination • Unfortunately, many pharmaceuticals contain in their native form only light atoms that at best have only weak anomalous scattering power and thus fail the strict Flack conditions. • Alternative approaches are offered by PLATON with scatter plots and the determination of the Hooft y parameter

Scatter Plot of Bijvoet Differences • Plot of the Observed Bijvoet (Friedel) Differences against the Calculated Differences. • A Least-Squares line is calculated • The Green least squares line should run from the lower left to the upper right corner for the correct absolute structure. • Vertical bars on data points indicate the su on the Bijvoet Difference. Example

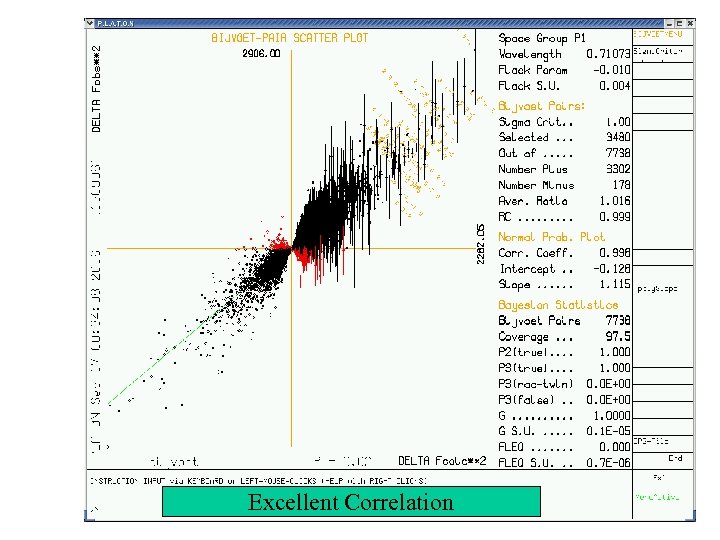Excellent Correlation

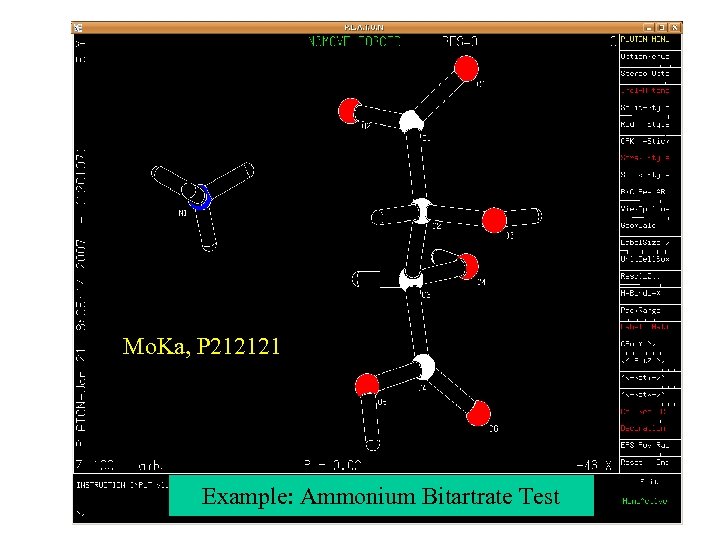Mo. Ka, P 212121 Example: Ammonium Bitartrate Test

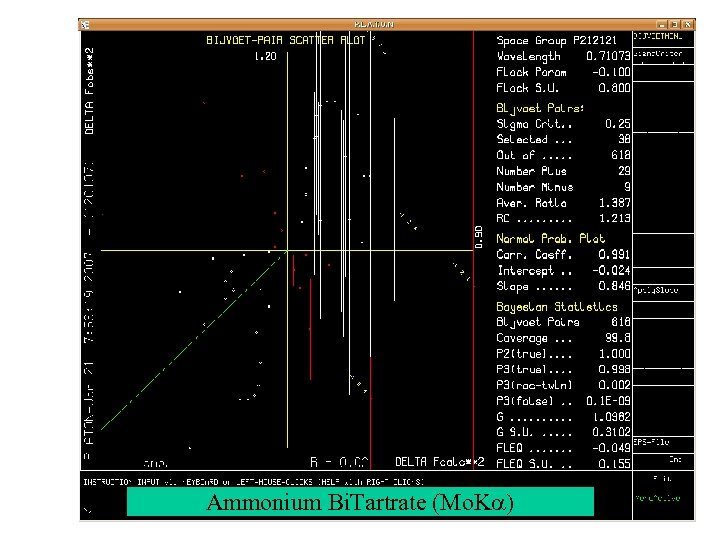Ammonium Bi. Tartrate (Mo. Ka)

Bayesian Approach • Rob Hooft (Bruker) has developed an alternative approach for the analyses of Bijvoet differences that is based on Bayesian statistics. (Paper under review) • Under the assumption that the material is enantiopure, the probability that the assumed absolute structure is correct, given the set of observed Bijvoet Pair Differences, is calculated. • An extension of the method also offers the Fleq y (Hooft y) parameter to be compared with the Flack x. • Example: Ascorbic Acid, P 21, Mo. Ka data

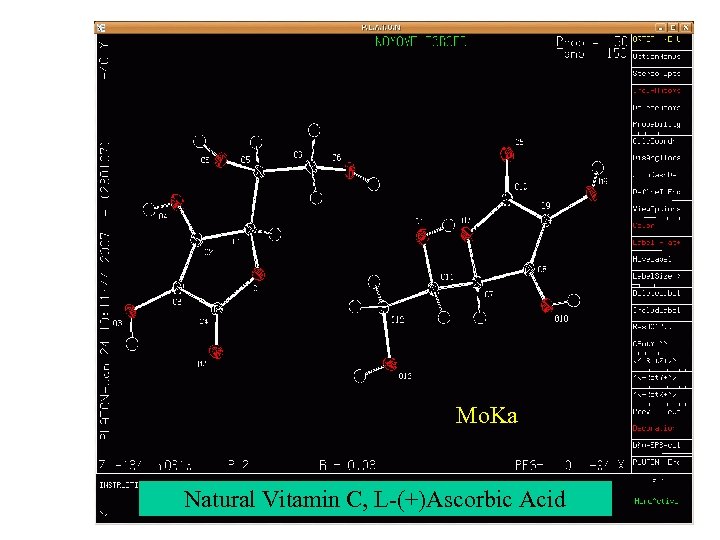Mo. Ka Natural Vitamin C, L-(+)Ascorbic Acid

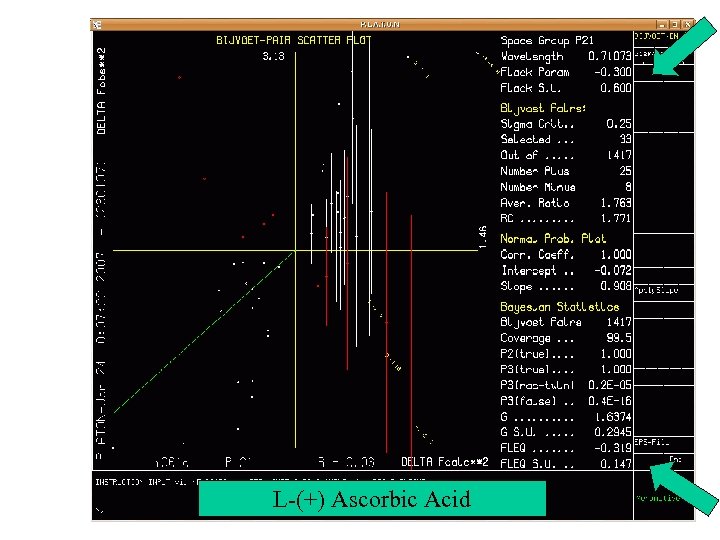L-(+) Ascorbic Acid

Hooft y Proper Procedure • Collect data with an essentially complete set of Bijvoet Pairs • Refine in the usual way (preferably) with BASF and TWIN instructions (SHELXL) • Structure Factors to be used in the analysis are recalculated in PLATON from the parameters in the CIF (No Flack x contribution).

Do we need Validation ? Some Statistics • • • Validation CSD Entries 2006 + 2007 Number of entries: 35760 # of likely Space Group Changes: 384 # of structures with voids: 3354 Numerous problems with H, O, OH, H 2 O etc. • Example

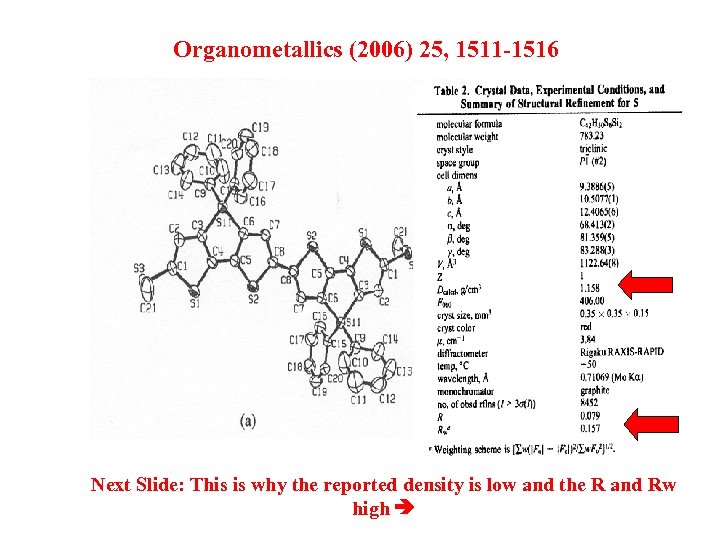Organometallics (2006) 25, 1511 -1516 Next Slide: This is why the reported density is low and the R and Rw high

Solvent Accessible Void of 235 Ang 3 out of 1123 Ang 3 Not Accounted for in the Refinement Model

SOLUTION A solution for the structure validation problem was pioneered by the International Union of Crystallography - Provide and archive crystallographic data in the computer readable CIF standard format. - Offer Automated validation, with a computer generated report for authors and referees. - Have journals enforce a structure validation protocol. - The IUCr journals and most major journals now indeed implement some form of validation procedure.

THE CIF DATA STANDARD - Driving Force: Syd Hall (IUCr/ Acta Cryst C) Early Adopted by XTAL & SHELX(T)L. Currently: Win. GX, Crystals, Texsan, Maxus etc. Acta Cryst. C/E – Electronic Submission Acta Cryst. : Automatic Validation at the Gate CIF data available for referees for detailed inspection (and optional calculations). - Data retrieval from the WEB for published papers - CCDC – Deposition in CIF-FORMAT.

VALIDATION QUESTIONS Single crystal validation addresses three simple but important questions: 1 – Is the reported information complete? 2 – What is the quality of the analysis? 3 – Is the Structure Correct?

IUCr CHECKCIF WEB-Service http: //checkcif. iucr. org reports the outcome of: • IUCr standard tests Consistency, Missing Data, Proper Procedure, Quality etc. • + Additional PLATON based tests Missed Symmetry, Twinning, Voids, Geometry, Displacement Parameters, Absolute Structure etc.

ALERT LEVELS • • ALERT A – Serious Problem ALERT B – Potentially Serious Problem ALERT C – Check & Explain ALERT G – Verify or Take Notice

ALERT TYPES 1 - CIF Construction/Syntax errors, Missing or Inconsistent Data. 2 - Indicators that the Structure Model may be Wrong or Deficient. 3 - Indicators that the quality of the results may be low. 4 - Cosmetic Improvements, Queries and Suggestions.

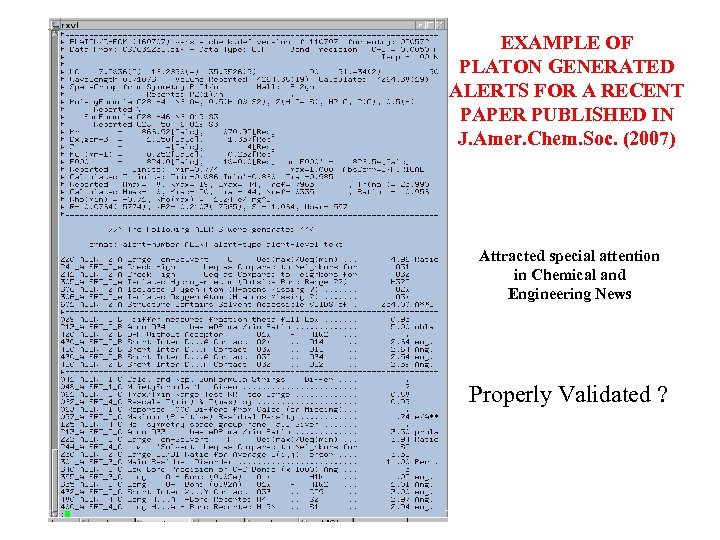EXAMPLE OF PLATON GENERATED ALERTS FOR A RECENT PAPER PUBLISHED IN J. Amer. Chem. Soc. (2007) Attracted special attention in Chemical and Engineering News Properly Validated ?

Problems Addressed by PLATON/CIF-CHECK - Missed Higher Space Group Symmetry Solvent Accessible Voids in the Structure Unusual Displacement Parameters Hirshfeld Rigid Bond test Misassigned Atom Type Population/Occupancy Parameters Mono Coordinated/Bonded Metals Isolated Atoms (e. g. O, H, Transition Metals)

More Problems Addressed by PLATON - Too Many Hydrogen Atoms on an Atom Missing Hydrogen Atoms Valence & Hybridization Short Intra/Inter-Molecular Contacts O-H without Acceptor Unusual Bond Length/Angle CH 3 Moiety Geometry To be extended with tests for new problems ‘invented’ by authors.

Additional Problems Addressed by PLATON/FCF-CHECK • • Information from. cif and. fcf files Report on the resolution of the data Report about randomly missing data Check the completeness of the data (e. g. for missing cusps of data • Report on Missed (Pseudo) Merohedral Twinning • Report on Friedel Pairs and Absolute Structure • Next Slide: ASYM VIEW Display for the inspection of the data completeness

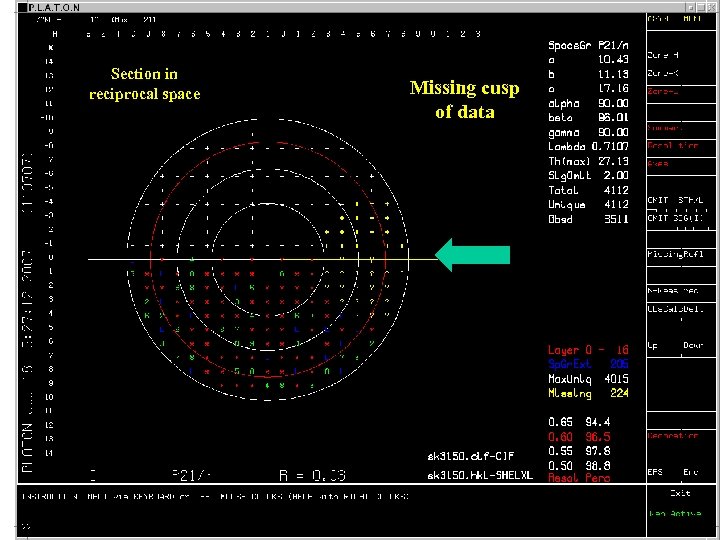Section in reciprocal space Missing cusp of data

Incorrectly Oriented O-H • The O-H moiety is generally, with very few exceptions, part of a D-H. . A system. • An investigation of structures in the CSD brings up many ‘exceptions’. • Closer analysis shows that misplacement of the OH hydrogen atom is in general the cause. • Molecules have an environment in the crystal ! • Example

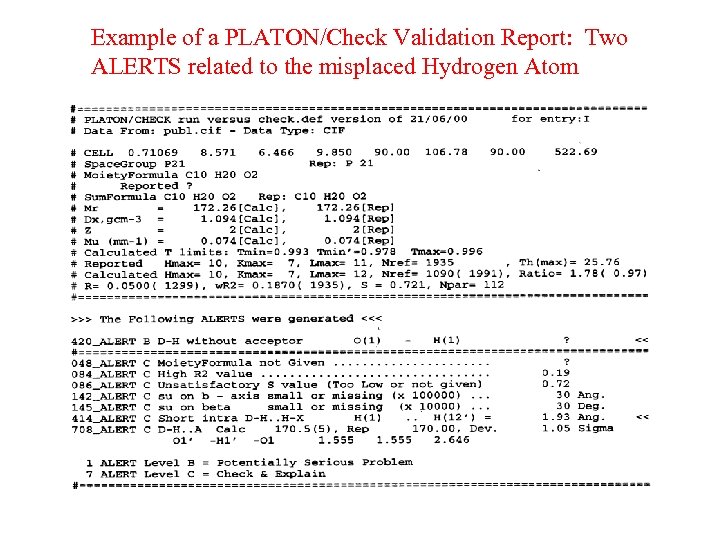Example of a PLATON/Check Validation Report: Two ALERTS related to the misplaced Hydrogen Atom

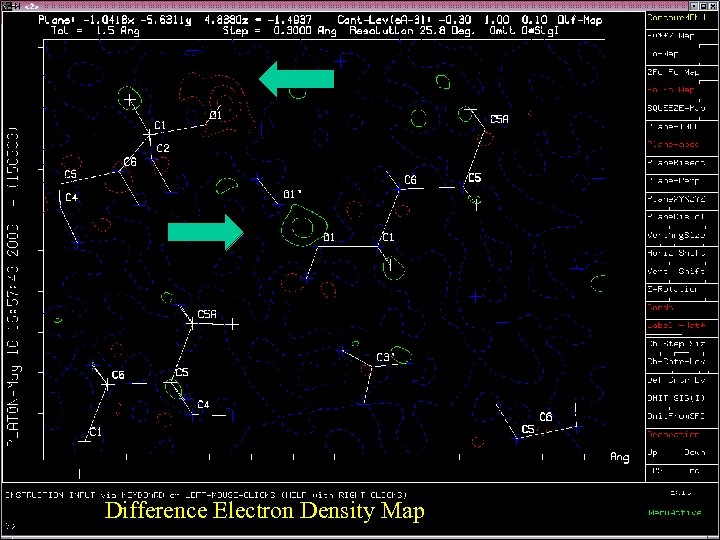Difference Electron Density Map

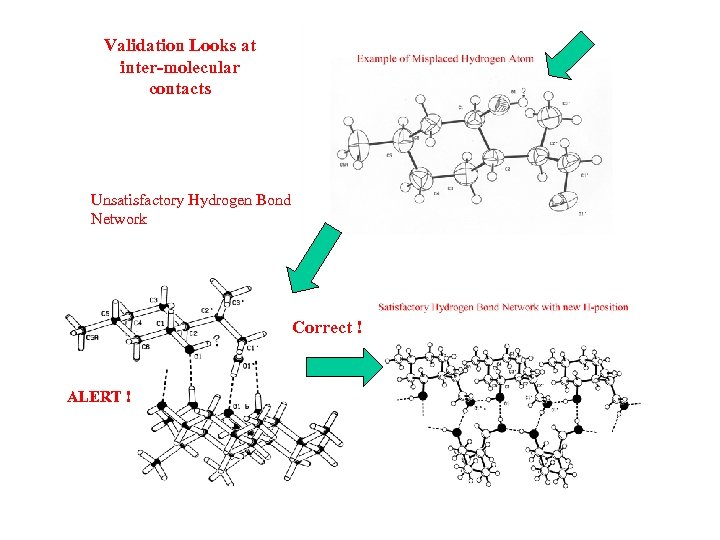Validation Looks at inter-molecular contacts Unsatisfactory Hydrogen Bond Network Correct ! ALERT !

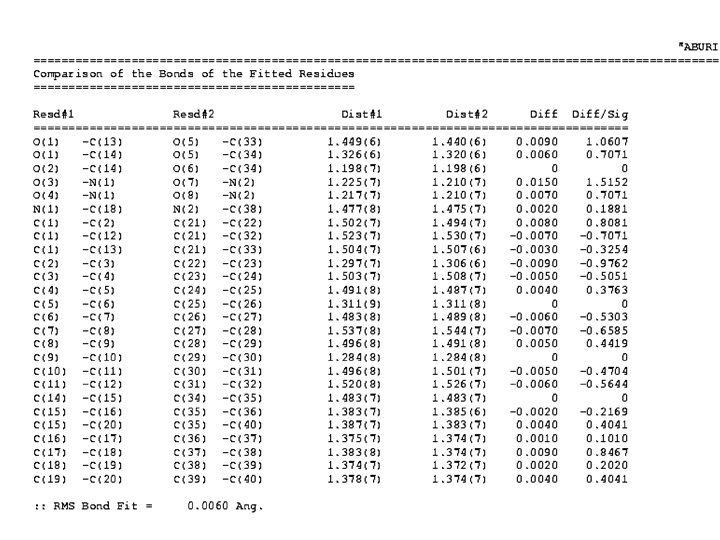
QUATERNION FIT • In many cases, an automatic molecule fit can be performed • A) Identical atom numbering • B) Sufficient number of Unique Atoms • C) By manual picking of a few atom pairs

QUATERNION FIT

Simulated Powder Patterns • It is not always apparent that two crystal structures are identical. The assigned unit cell or space group can differ. • Comparison of the associated calculated powder patterns should solve the issue. • Example for the CSD:

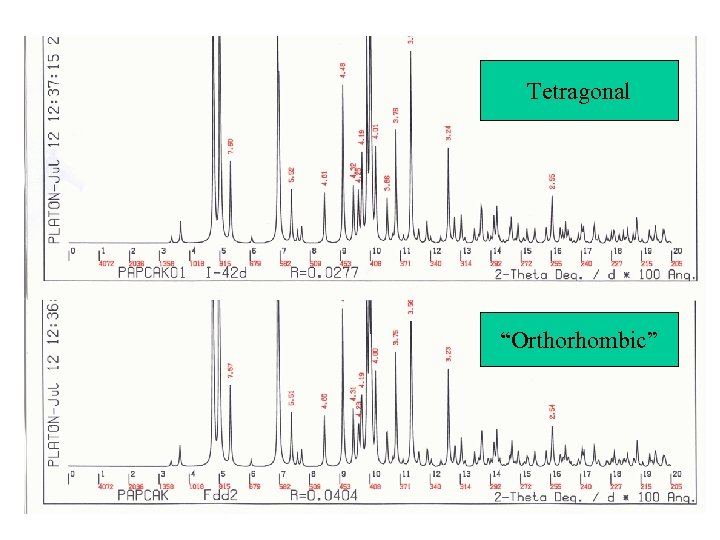Tetragonal “Orthorhombic”

THE MESSAGE - Validation should not be postponed to the publication phase. All validation issues should be taken care of during the analysis. - Everything unusual in a structure is suspect, mostly incorrect (artifact) and should be investigated and discussed in great detail and supported by additional independent evidence. - The CSD can be very helpful when looking for possible precedents.

CONCLUSION Validation Procedures are excellent Tools to: - Set Quality Standards (Not just on R-Value) - Save a lot of Time in Checking, both by the Investigators and the Journals (referees) - Point at Interesting Features (Pseudo-Symmetry, short Interactions etc. ) to be discussed. - Surface a problem that only an experienced Crystallographer might be able to Address - Proof of a GOOD structure.

Additional Info http: //www. cryst. chem. uu. nl (including a copy of this powerpoint presentation) Thanks for your attention !!