Символом F обозначено одно из указанных ниже логических

Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F? 1) ¬(X Y) Z 2) ¬(X ¬Y) Z 3) ¬(X Y) Z 4) (X Y) Z XYZF 0001 0011 0101

Для какого из указанных значений X истинно высказывание ¬((X > 2)→(X > 3))? 1) 1 2) 2 3) 3 4) 4

Какое из приведённых имен удовлетворяет логическому условию: (первая буква согласная → вторая буква согласная) / (предпоследняя буква гласная → последняя буква гласная)? 1) КРИСТИНА 2) МАКСИМ 3) СТЕПАН 4) МАРИЯ

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &. 1) принтеры & сканеры & продажа 2) принтеры & продажа 3) принтеры | продажа 4) принтеры | сканеры | продажа

Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент: Ключевое слово сканер принтер монитор Количество сайтов, для которых данное слово является ключевым 200 250 450 Сколько сайтов будет найдено по запросу (принтер | сканер) & монитор если по запросу принтер | сканер было найдено 450 сайтов, по запросу принтер & монитор – 40, а по запросу сканер & монитор – 50.

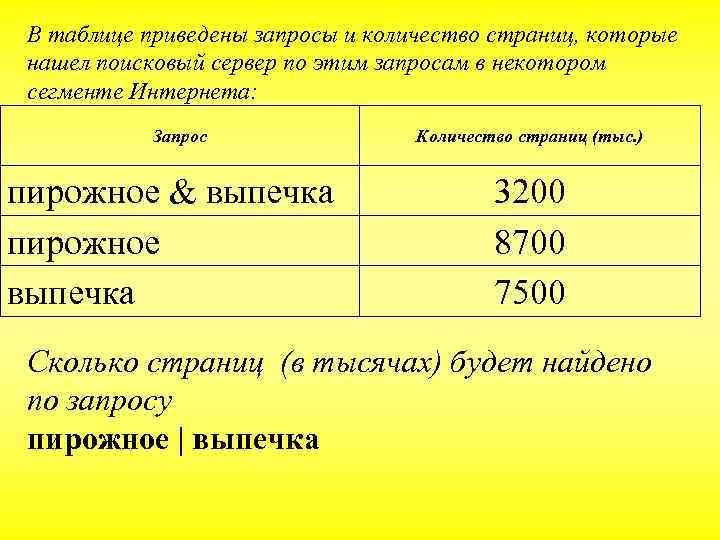
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета: Запрос пирожное & выпечка пирожное выпечка Количество страниц (тыс. ) 3200 8700 7500 Сколько страниц (в тысячах) будет найдено по запросу пирожное | выпечка

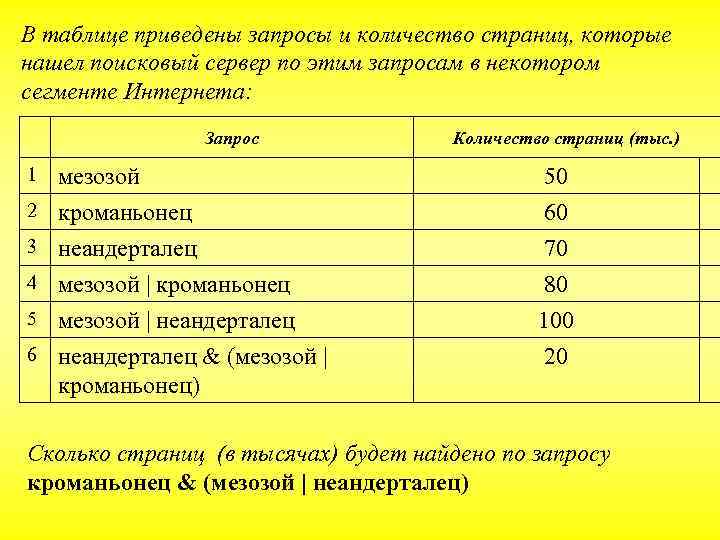
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета: Запрос 1 Количество страниц (тыс. ) мезозой 2 кроманьонец 3 неандерталец 50 60 70 4 80 100 20 мезозой | кроманьонец 5 мезозой | неандерталец 6 неандерталец & (мезозой | кроманьонец) Сколько страниц (в тысячах) будет найдено по запросу кроманьонец & (мезозой | неандерталец)

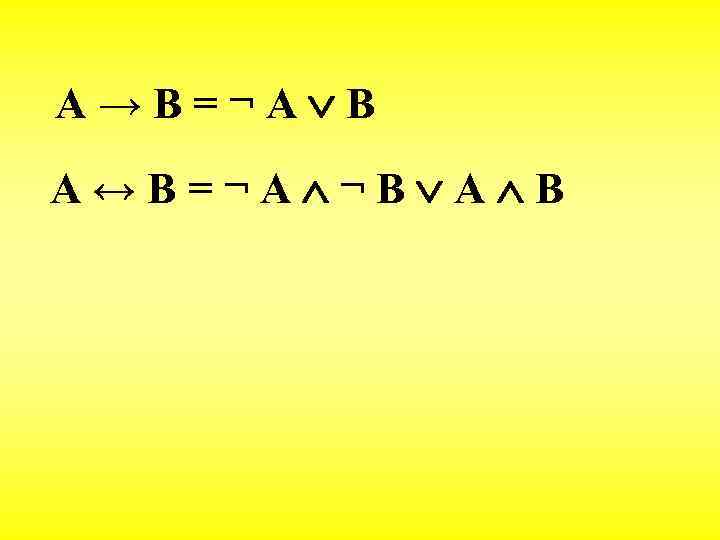
A → B = ¬ A B A ↔ B = ¬ A ¬ B A B

Сколько различных решений имеет логическое уравнение (¬X 1 X 2) (¬X 2 X 3) (¬X 3 X 4) (¬X 4 X 5) (¬X 5 X 6) = 1 где x 1, x 2, …, x 6 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Сколько различных решений имеет система уравнений ¬X 1 X 2 = 1 ¬X 2 X 3 = 1. . . ¬X 9 X 10 = 1 где x 1, x 2, …, x 10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Сколько различных решений имеет система уравнений ¬(X 1 X 2) (X 3 X 4) = 1 ¬(X 3 X 4) (X 5 X 6) = 1 ¬(X 5 X 6) (X 7 X 8) = 1 ¬(X 7 X 8) (X 9 X 10) = 1 где x 1, x 2, …, x 10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Сколько различных решений имеет система уравнений (X 1 X 2) (¬X 1 ¬X 2) (¬X 3 X 4) (X 3 ¬X 4) = 1 (X 3 X 4) (¬X 3 ¬X 4) (¬X 5 X 6) (X 5 ¬X 6) = 1 (X 5 X 6) (¬X 5 ¬X 6) (¬X 7 X 8) (X 7 ¬X 8) = 1 (X 7 X 8) (¬X 7 ¬X 8) (¬X 9 X 10) (X 9 ¬X 10) = 1 где x 1, x 2, …, x 10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Сколько различных решений имеет система уравнений ((X 1 X 2) (X 3 X 4)) (¬(X 1 X 2) ¬(X 3 X 4)) = 1 ((X 3 X 4) (X 5 X 6)) (¬(X 3 X 4) ¬(X 5 X 6)) = 1 ((X 5 X 6) (X 7 X 8)) (¬(X 5 X 6) ¬(X 7 X 8)) = 1 ((X 7 X 8) (X 9 X 10)) (¬(X 7 X 8) ¬(X 9 X 10)) = 1 где x 1, x 2, …, x 10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Сколько различных решений имеет система уравнений (X 2 X 1) (X 2 X 3) (¬X 2 ¬ X 3)= 1 (X 3 X 1) (X 3 X 4) (¬X 3 ¬ X 4)= 1. . . (X 9 X 1) (X 9 X 10) (¬X 9 ¬ X 10)= 1 (X 10 X 1) = 0 где x 1, x 2, …, x 10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Сколько различных решений имеет система уравнений (X 1 X 2) (¬X 1 ¬X 2) (X 1 X 3) = 1 (X 2 X 3) (¬X 2 ¬X 3) (X 2 X 4) = 1. . . (X 8 X 9) (¬X 8 ¬X 9) (X 8 X 10) = 1 где x 1, x 2, …, x 10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Сколько различных решений имеет система уравнений (X 1 X 2) (¬X 1 ¬X 2) (X 2 X 3) (¬X 2 ¬X 3) = 1 (X 2 X 3) (¬X 2 ¬X 3) (X 3 X 4) (¬X 3 ¬X 4) = 1. . . (X 8 X 9) (¬X 8 ¬X 9) (X 9 X 10) (¬X 9 ¬X 10) = 1 где x 1, x 2, …, x 10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Ответы: Слайд № 1. 3 Слайд № 2. 3 Слайд № 3. 1 Слайд № 4. 1234 Слайд № 5. 90 Слайд № 6. 13000 Слайд № 7. 30 Слайд № 9. 7 Слайд № 10. 11 Слайд № 11. 192 Слайд № 12. 192 Слайд № 13. 64 Слайд № 14. 18 Слайд № 15. 20 Слайд № 16. 178