Simulation of Discrete Damage in Composite Overheight Compact

Simulation of Discrete Damage in Composite Overheight Compact Tension Specimens David Mollenhauer, Logan Ward Air Force Research Laboratory, USA Endel Iarve, Sirina Putthanarat, Kevin Hoos University of Dayton Research Institute, USA Stephen Hallett, Xiangqian Li University of Bristol, United Kingdom Comp. Test 2011 Lausanne, Switzerland 14 -16 February 2011

Outline • Motivation • Background • Numerical Model Details • Results • Blocked quasi-isotropic & cross-ply • Statistical strength effects • Dispersed ply quasi-isotropic • Conclusion & Future

Motivation Normalized Axial Strain from [0/45/90/-45]s Composite Y X No damage Extensive Damage

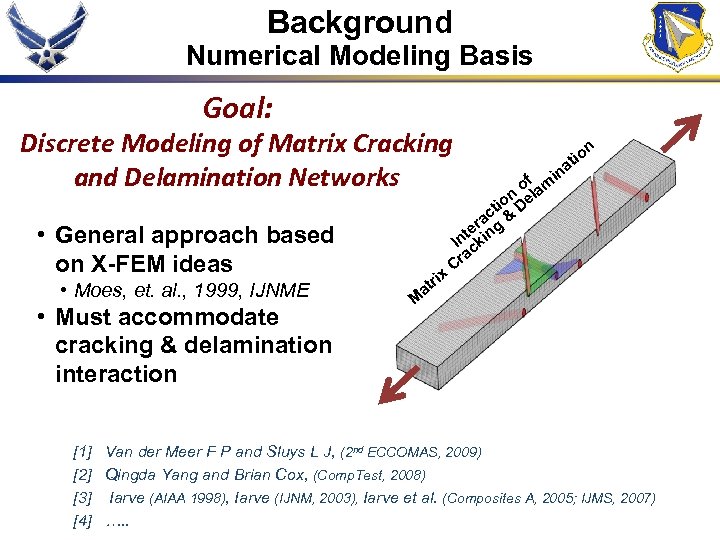Background Numerical Modeling Basis Goal: Discrete Modeling of Matrix Cracking and Delamination Networks • General approach based on X-FEM ideas • Moes, et. al. , 1999, IJNME • Must accommodate cracking & delamination interaction x tri a n tio a in of am n l io De t ac g & r te in In ck a Cr M [1] Van der Meer F P and Sluys L J, (2 nd ECCOMAS, 2009) [2] Qingda Yang and Brian Cox, (Comp. Test, 2008) [3] Iarve (AIAA 1998), Iarve (IJNM, 2003), Iarve et al. (Composites A, 2005; IJMS, 2007) [4] …. .

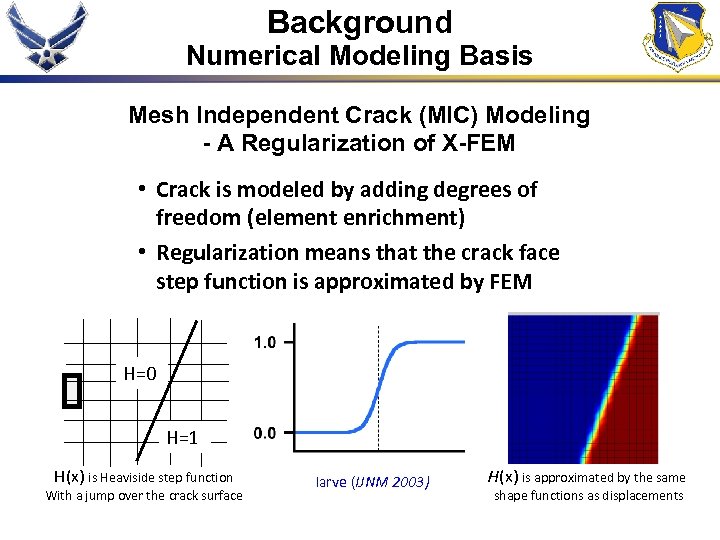Background Numerical Modeling Basis Mesh Independent Crack (MIC) Modeling - A Regularization of X-FEM • Crack is modeled by adding degrees of freedom (element enrichment) • Regularization means that the crack face step function is approximated by FEM H=0 H=1 H(x) is Heaviside step function With a jump over the crack surface Iarve (IJNM 2003) H(x) is approximated by the same shape functions as displacements

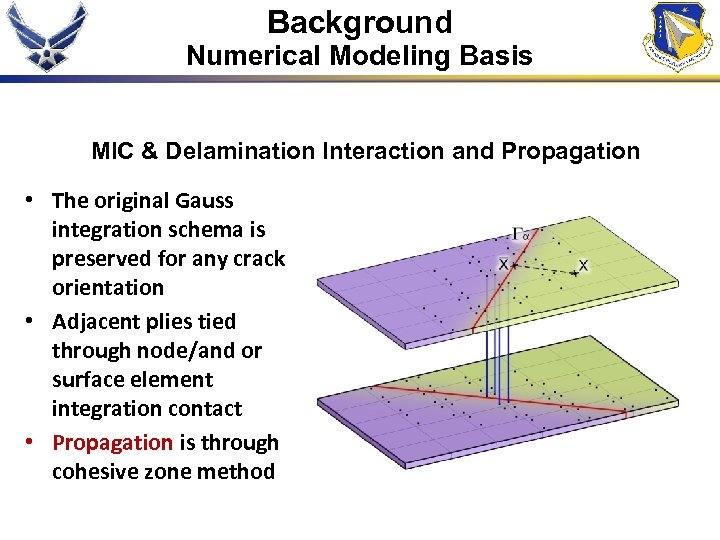Background Numerical Modeling Basis MIC & Delamination Interaction and Propagation • The original Gauss integration schema is preserved for any crack orientation • Adjacent plies tied through node/and or surface element integration contact • Propagation is through cohesive zone method

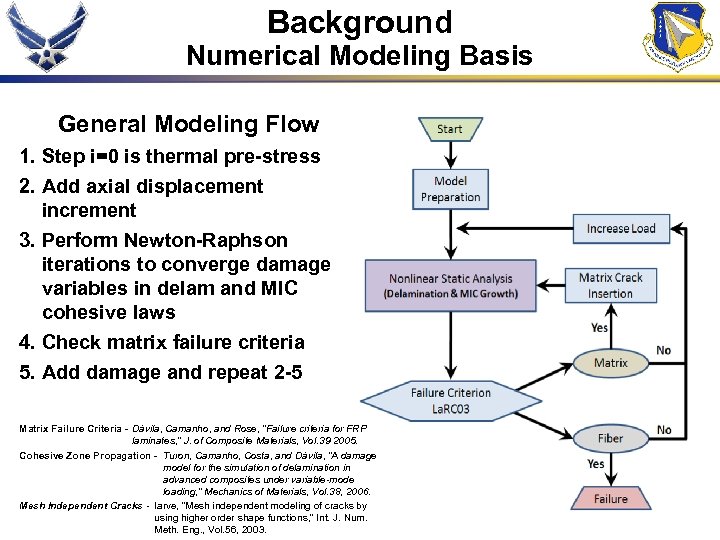Background Numerical Modeling Basis General Modeling Flow 1. Step i=0 is thermal pre-stress 2. Add axial displacement increment 3. Perform Newton-Raphson iterations to converge damage variables in delam and MIC cohesive laws 4. Check matrix failure criteria 5. Add damage and repeat 2 -5 Matrix Failure Criteria - Dávila, Camanho, and Rose, “Failure criteria for FRP laminates, ” J. of Composite Materials, Vol. 39 2005. Cohesive Zone Propagation - Turon, Camanho, Costa, and Dávila, “A damage model for the simulation of delamination in advanced composites under variable-mode loading, ” Mechanics of Materials, Vol. 38, 2006. Mesh Independent Cracks - Iarve, “Mesh independent modeling of cracks by using higher order shape functions, ” Int. J. Num. Meth. Eng. , Vol. 56, 2003.

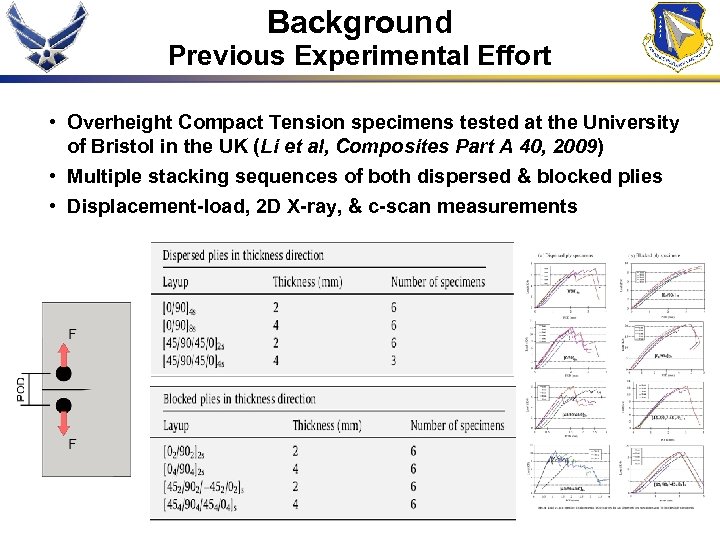Background Previous Experimental Effort • Overheight Compact Tension specimens tested at the University of Bristol in the UK (Li et al, Composites Part A 40, 2009) • Multiple stacking sequences of both dispersed & blocked plies • Displacement-load, 2 D X-ray, & c-scan measurements

Numerical Model Details • In-house code BSAM (B-spline analysis method) used • Geometry matched to Bristol’s test specimens • Blocked Ply Specimens (IM 7/8552) • [452/902/-452/02] s Table 1. Properties for IM 7/8552 Lamina • [04/904] 2 s Material Property Value • Dispersed Ply Specimen (IM 7/8552) E (GPa) 161. 0 E , E (GPa) 11. 38 • [45/90/-45/0] 2 s Ref 1 11 22 Ref 1 33 G 12, G 13 (GPa) G 23 (GPa) n 12, n 13 n 23 Ref 1 3. 98 0. 32 0. 44 Ref 1 a 1 (1/◦C) a 2 5. 17 0. 00 3. 00 e-05 (1/◦C) GIC (N/mm) Ref 1 0. 2 GIIC (N/mm) Ref 1 1. 0 YT (MPa) 60. 0 YC (MPa) 275. 0 S (MPa) 90. 0 [1] Hallett, S. R. , Jiang, W. G. , Khan, B. , and Wisnom, M. R. , “Modeling the interaction between matrix cracks and delamination damage in scaled quasi-isotropic specimens, ” Compos Sci Technol, 68(1): pp. 80 -89, 2008.

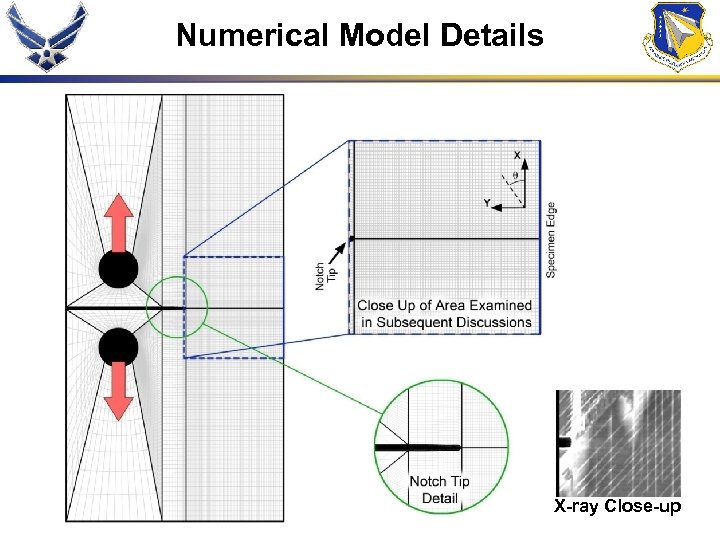Numerical Model Details X-ray Close-up

Matrix Damage Comparison Blocked Quasi [452/902/-452/02] s Specimen Shifted Results POD = 2. 11 mm Specimen One Stacked X-Ray

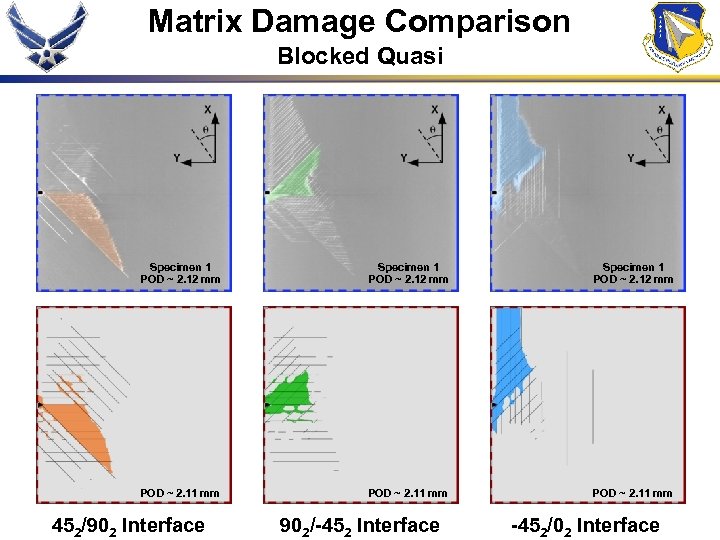Matrix Damage Comparison Blocked Quasi Specimen 1 POD ~ 2. 12 mm POD ~ 2. 11 mm 452/902 Interface 902/-452 Interface -452/02 Interface

POD vs Load Comparison Blocked Quasi [452/902/-452/02] s Specimen

Matrix Damage Evolution Blocked Quasi [452/902/-452/02] s Specimen

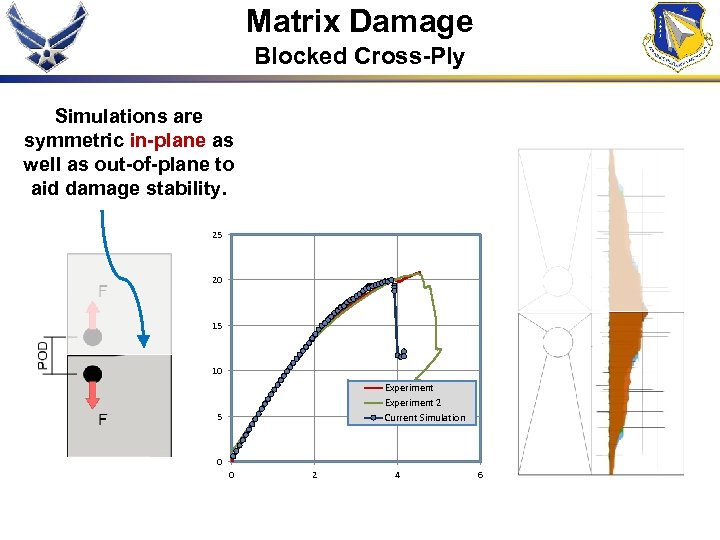Matrix Damage Blocked Cross-Ply Simulations are symmetric in-plane as well as out-of-plane to aid damage stability. 25 20 15 10 Experiment 2 Current Simulation 5 0 0 2 4 6

Matrix Damage Evolution Blocked Cross Ply [04/904] 2 s Specimen • Movie has been mirrored about symmetry plane

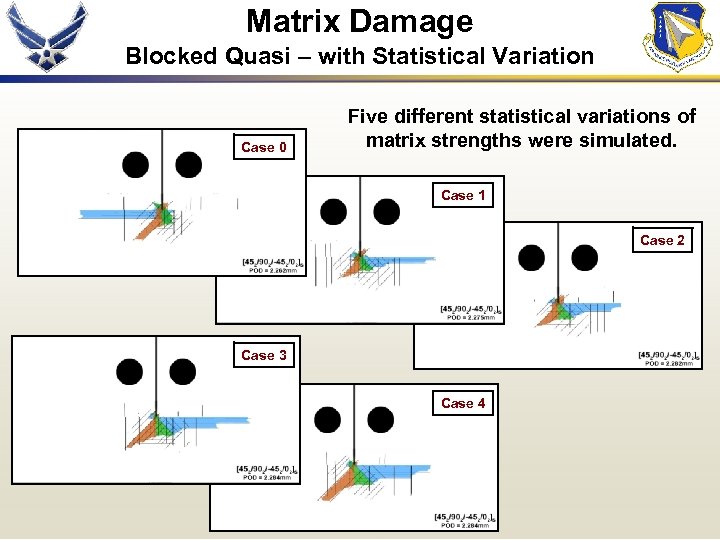Matrix Damage Blocked Quasi – with Statistical Variation Case 0 Five different statistical variations of matrix strengths were simulated. Case 1 Case 2 Case 3 Case 4

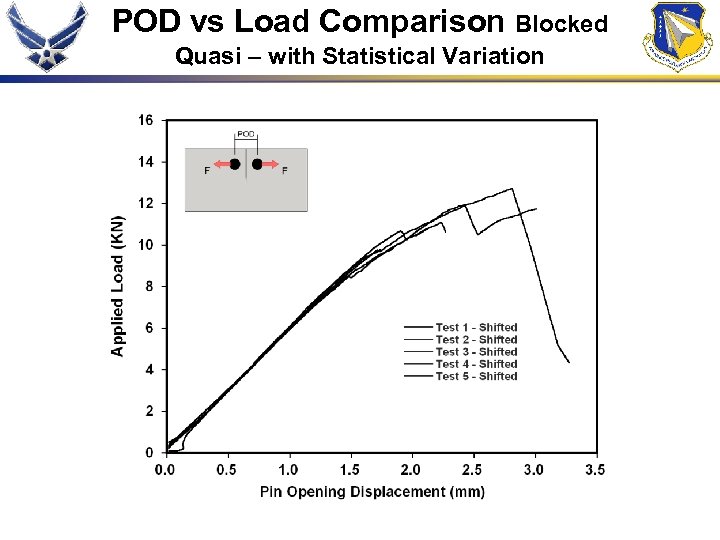POD vs Load Comparison Blocked Quasi – with Statistical Variation

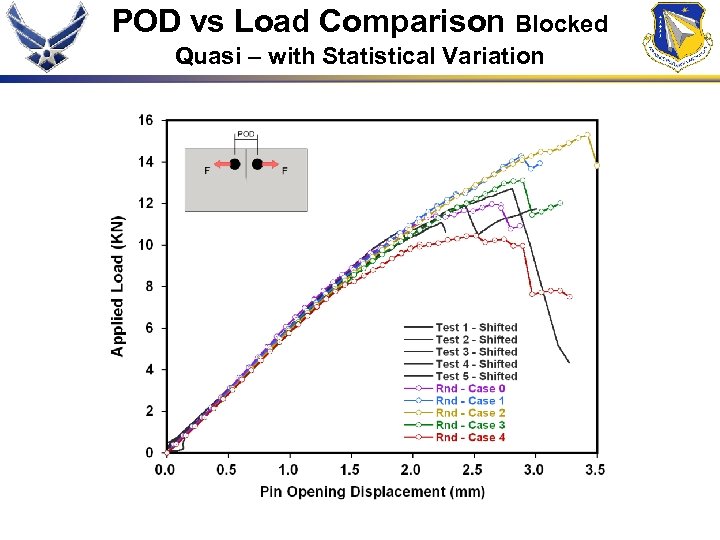POD vs Load Comparison Blocked Quasi – with Statistical Variation

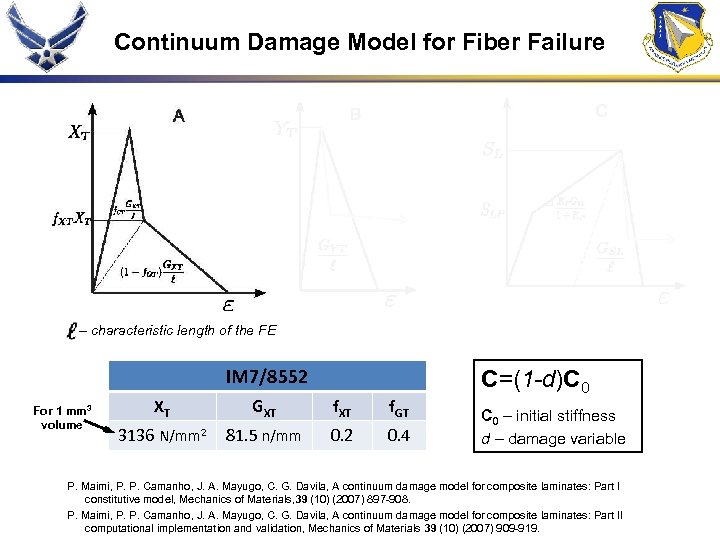Continuum Damage Model for Fiber Failure – characteristic length of the FE IM 7/8552 For 1 mm 3 volume XT GXT f. GT 3136 N/mm 2 81. 5 n/mm 0. 2 0. 4 C=(1 -d)C 0 – initial stiffness d – damage variable P. Maimi, P. P. Camanho, J. A. Mayugo, C. G. Davila, A continuum damage model for composite laminates: Part I constitutive model, Mechanics of Materials, 39 (10) (2007) 897 -908. P. Maimi, P. P. Camanho, J. A. Mayugo, C. G. Davila, A continuum damage model for composite laminates: Part II computational implementation and validation, Mechanics of Materials 39 (10) (2007) 909 -919.

Matrix & Fiber Damage Dispersed Quasi [45/90/-45/0] 2 s Specimen experimental X-ray simulation damage pattern • Continuum damage mechanics routine used for fiber damage courtesy of Carlos Davila of NASA La. RC

Matrix & Fiber Damage Dispersed Quasi [45/90/-45/0/45/90/-45/0] s Image from Test Specimen #3

Matrix & Fiber Damage Dispersed Quasi [45/90/-45/0/45/90/-45/0] s Image from Test Specimen #3

Matrix & Fiber Damage Dispersed Quasi [45/90/-45/0/45/90/-45/0] s Image from Test Specimen #3

Matrix & Fiber Damage Dispersed Quasi [45/90/-45/0/45/90/-45/0] s Image from Test Specimen #3

Matrix & Fiber Damage Dispersed Quasi [45/90/-45/0/45/90/-45/0] s Image from Test Specimen #3

Matrix & Fiber Damage Dispersed Quasi [45/90/-45/0/45/90/-45/0] s Image from Test Specimen #3

Matrix & Fiber Damage Dispersed Quasi [45/90/-45/0/45/90/-45/0] s Image from Test Specimen #3

Conclusions & Future • Concusions: • Simulated load-displacement behavior correlates well with actual specimen behavior • Simulated discrete damage patterns correlate extremely well with X-ray CT images • At similar applied load levels • Predicted complex specimen behavior obtained using only lamina-level, measurable properties and application of “simple” descriptions of damage. • Future Efforts: • Validate current fiber failure methodology • Implement alternative fiber failure methodology

Acknowledgements • Partial funding for this work from NASA AAD-2 (NNX 08 AB 05 A-G) and AFRL (FA 8650 -05 -D-5052) • Many thanks to Dr Cheryl Rose and Dr Carlos Davila of NASA La. RC for collaboration and advice. • The authors also wish to acknowledge their collaboration with Anoush Poursartip, Reza Vaziri, and Navid Zobeiry at the University of British Columbia in conducting the OCT experimental testing

X-Ray Computed Tomography Top View X-ray imaging panel Image i Side View OCT Specimen 3 D “voxel” data visualizing internal specimen structure

X-Ray Computed Tomography Top View X-ray imaging panel Image j Side View OCT Specimen 3 D “voxel” data visualizing internal specimen structure

X-Ray Computed Tomography Top View X-ray imaging panel Image k Side View OCT Specimen 3 D “voxel” data visualizing internal specimen structure

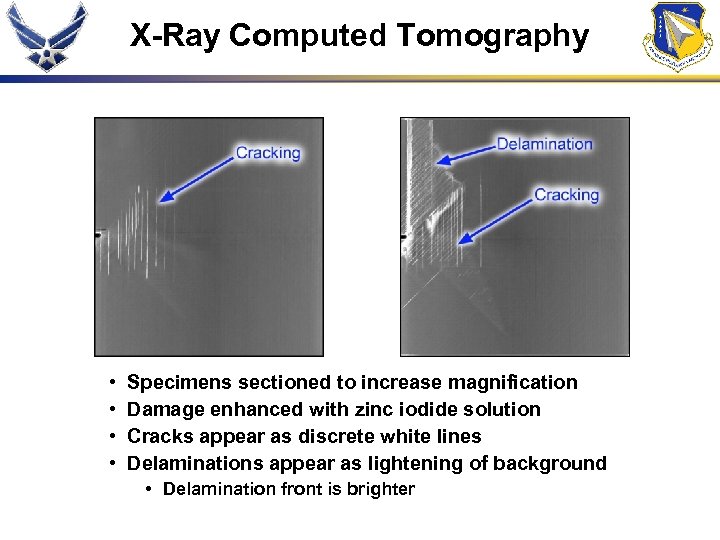X-Ray Computed Tomography • • Specimens sectioned to increase magnification Damage enhanced with zinc iodide solution Cracks appear as discrete white lines Delaminations appear as lightening of background • Delamination front is brighter

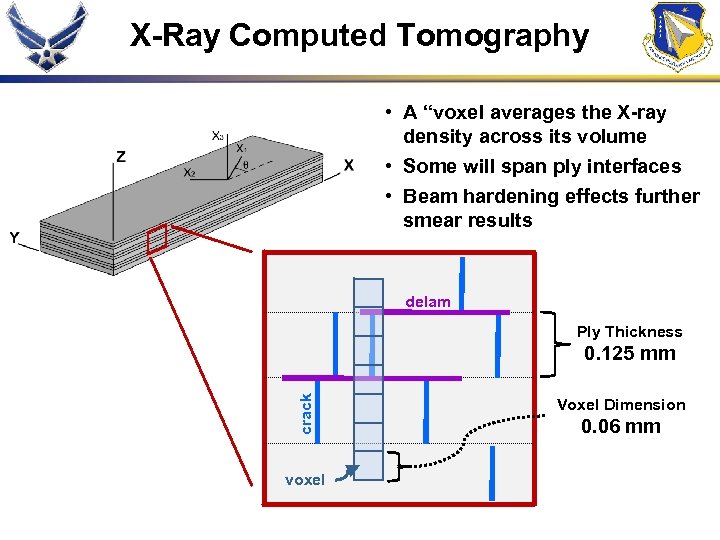X-Ray Computed Tomography • A “voxel averages the X-ray density across its volume • Some will span ply interfaces • Beam hardening effects further smear results delam Ply Thickness crack 0. 125 mm voxel Voxel Dimension 0. 06 mm

Experimental Results • • Load Displacement Results from the [452/902/-452/02] s Specimen Data shifted to extrapolate linear portion to zero Coarse X-ray CT results at POD = 1. 74, 2. 12, & 2. 26 mm Detailed X-ray CT results at POD = 1. 74 mm & 2. 26 mm Original Results from Li et al Shifted Results

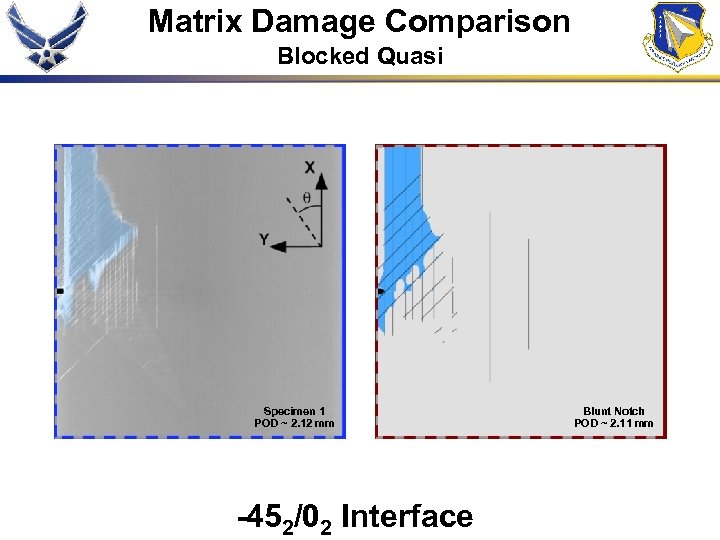Matrix Damage Comparison Blocked Quasi Specimen 1 POD ~ 2. 12 mm -452/02 Interface Blunt Notch POD ~ 2. 11 mm

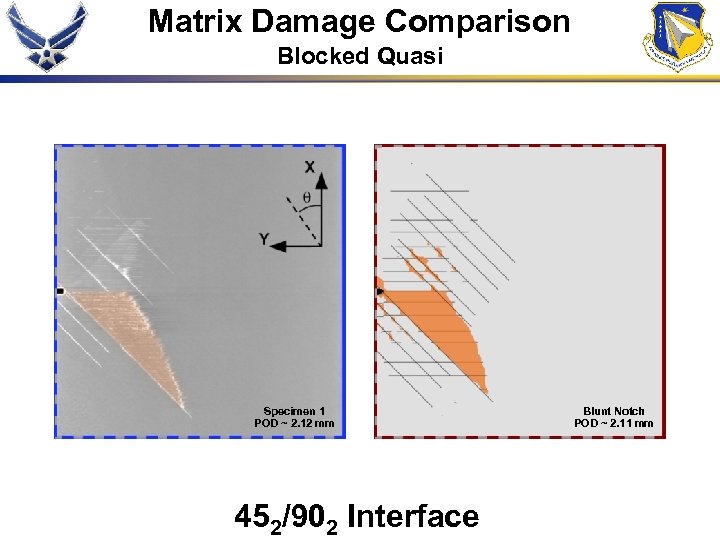Matrix Damage Comparison Blocked Quasi Specimen 1 POD ~ 2. 12 mm 452/902 Interface Blunt Notch POD ~ 2. 11 mm