Симплекс-метод метод последовательного улучшения плана Основная идея

Скачать презентацию Симплекс-метод метод последовательного улучшения плана Основная идея

Симплекс-метод_ДО.ppt

Количество слайдов: 70

Симплекс-метод (метод последовательного улучшения плана)

Основная идея симплекс-метода Экстремум целевой функции всегда достигается в угловых точках области допустимых решений. Симплекс-метод реализует перебор угловых точек области допустимых решений в направлении улучшения значения целевой функции. Прежде всего, находится какое-либо допустимое начальное (опорное) решение, т. е. какая-либо угловая точка области допустимых решений. Процедура метода позволяет ответить на вопрос, является ли это решение оптимальным. Если это так, то задача решена. Если нет, то выполняется переход к смежной угловой точке области допустимых решений, где значение целевой функции улучшается. Если некоторая угловая точка имеет несколько смежных, то вычислительная процедура метода обеспечивает переход к той из них, для которой улучшение целевой функции будет наибольшим. Процесс перебора угловых точек области допустимых решений повторяется, пока не будет найдена точка, которой соответствует экстремум целевой функции.

Метод позволяет определить является ли оптимальное решение единственным или имеет место множество оптимальных решений (так называемый альтернативный оптимум). Также метод позволяет выявить особые случаи: 1. 2. отсутствие допустимых решений; отсутствие оптимальных решений. Алгоритм: 1. 2. 3. 4. 5. Находим начальное допустимое решение Проверяем решение на оптимальность, если ДА => решение задачи найдено, если НЕТ => шаг 3 Среди свободных переменных находим ту, которую нужно включить в базис (этой переменной соответствует ведущий столбец симплекс-таблицы) Среди базисных переменных находим ту, которую следует вывести из базиса, т. е. сделать свободной переменной (этой переменной соответствует ведущая строка симплекс-таблицы) Пересчитав симплекс-таблицу переходим к следующему базисному допустимому решению. Возвращаемся к шагу 2.

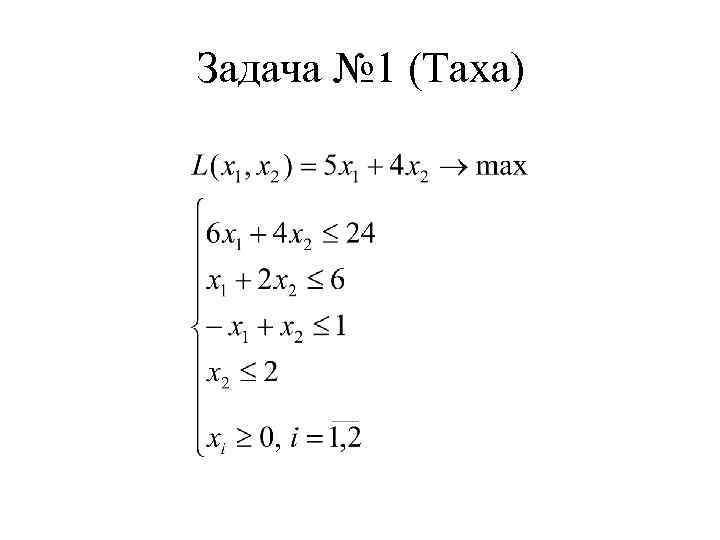Задача № 1 (Таха)

Задача № 1 (Таха) приведем задачу к каноническому виду Правые части всех ограничений должны быть неотрицательными.

Определение начального допустимого решения • • • Представить задачу в канонической форме. Для нахождения начального решения задачи требуется выразить m переменных (m - количество уравнений) через остальные n-m переменных, принять эти n-m переменных равными нулю и, таким образом, найти значения m переменных (в примере № 1 m=4 и n=6). Переменные, значения которых принимаются равными нулю, называются свободными, а остальные m переменных - базисными. Значения базисных переменных должны быть неотрицательны. Найденное таким образом решение называется начальным допустимым базисным решением. Это решение соответствует всем ограничениям. Начальное решение проще всего найти в случае, когда в каждом ограничении есть переменная, которая входит в него с коэффициентом 1 и при этом отсутствует в других ограничениях. Такие переменные принимаются в качестве базисных (они образуют начальный базис задачи). Остальные (небазисные) переменные принимаются равными нулю. Таким образом, базисные переменные принимают значения, равные правым частям ограничений.

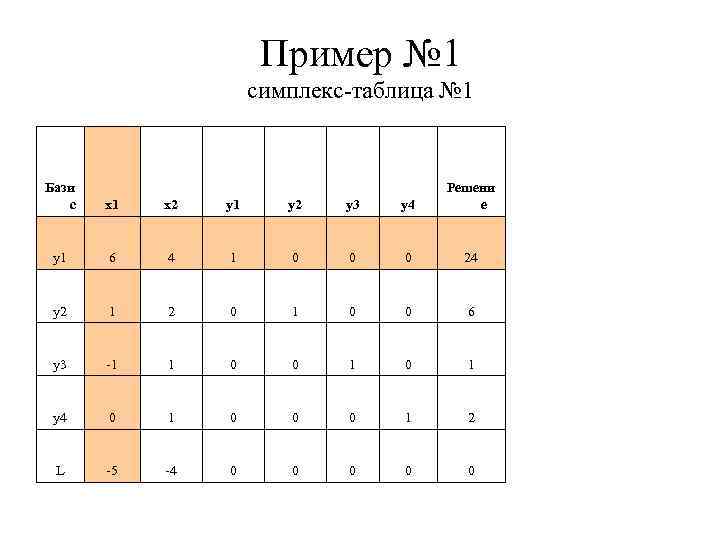Пример № 1 симплекс-таблица № 1 Бази с x 1 x 2 y 1 y 2 y 3 y 4 Решени е y 1 6 4 1 0 0 0 24 y 2 1 2 0 1 0 0 6 y 3 -1 1 0 0 1 y 4 0 1 0 0 0 1 2 L -5 -4 0 0 0

Пример № 1 симплекс-таблица № 2 Базис x 1 x 2 y 1 y 2 y 3 y 4 Решение x 1 1 2/3 1/6 0 0 0 4 y 2 0 1 1/3 - 1/6 1 0 0 2 y 3 0 1 2/3 1/6 0 1 0 5 y 4 0 0 0 1 2 L 0 0 20 1 - 2/3 0 5/6

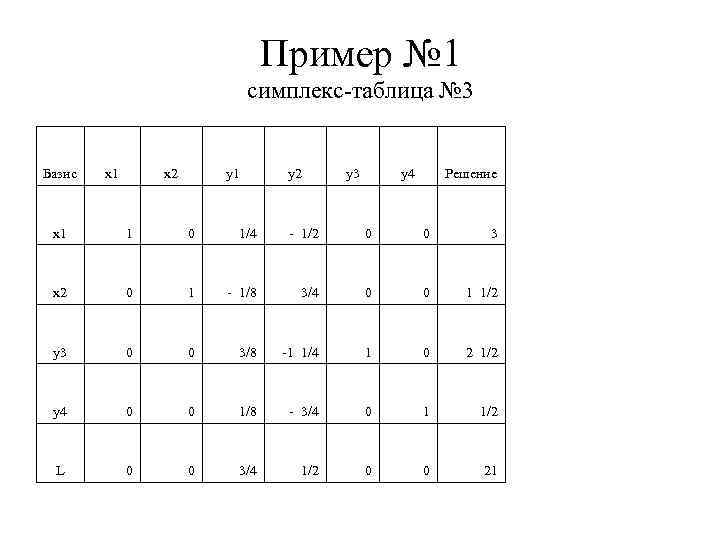Пример № 1 симплекс-таблица № 3 Базис x 1 x 2 y 1 y 2 y 3 y 4 Решение x 1 1 0 1/4 - 1/2 0 0 3 x 2 0 1 - 1/8 3/4 0 0 1 1/2 y 3 0 0 3/8 -1 1/4 1 0 2 1/2 y 4 0 0 1/8 - 3/4 0 1 1/2 L 0 0 3/4 1/2 0 0 21

Пересчет симплексной таблицы Процесс вычисления нового базисного решения состоит из двух этапов. 1. Вычисление элементов новой ведущей строки. Новая ведущая строка = текущая ведущая строка / ведущий элемент. 2. Вычисление элементов остальных строк, включая L-строку. Новая строка = текущая строка - ее коэффициент в ведущем столбце х новая ведущая строка.

Пересчет симплексной таблицы (продолжение) Пусть нужно поменять x 2 и y 2. Выразим из 2 -го уравнения x 2 и подставим в 1 -е уравнение

Пересчет симплексной таблицы (продолжение)

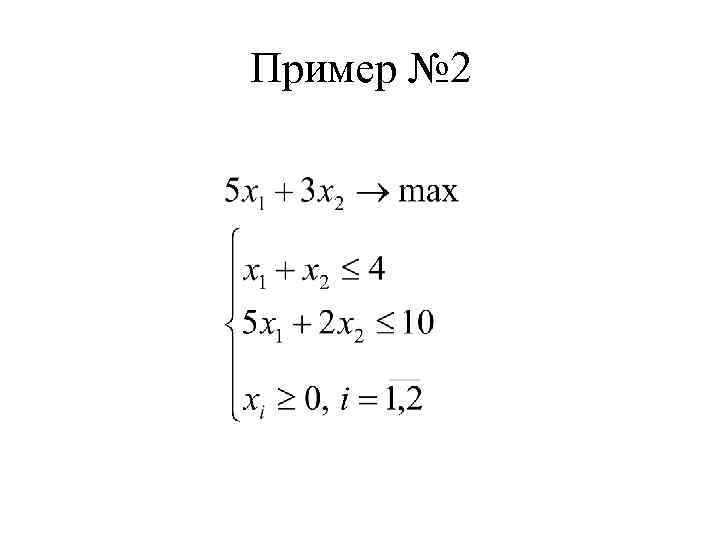Пример № 2

Пример № 2 (продолжение) приведем задачу к каноническому виду

Пример № 2 (продолжение) составим симплекс-таблицу Базис x 1 x 2 y 1 y 2 Решение y 1 1 0 4 y 2 5 2 0 1 10 L -5 -3 0 0 0

Пример № 2 (продолжение) составим симплекс-таблицу Базис x 1 x 2 y 1 y 2 Решение Отн. y 1 1 0 4 4 y 2 5 2 0 1 10 2 L -5 -3 0 0 0

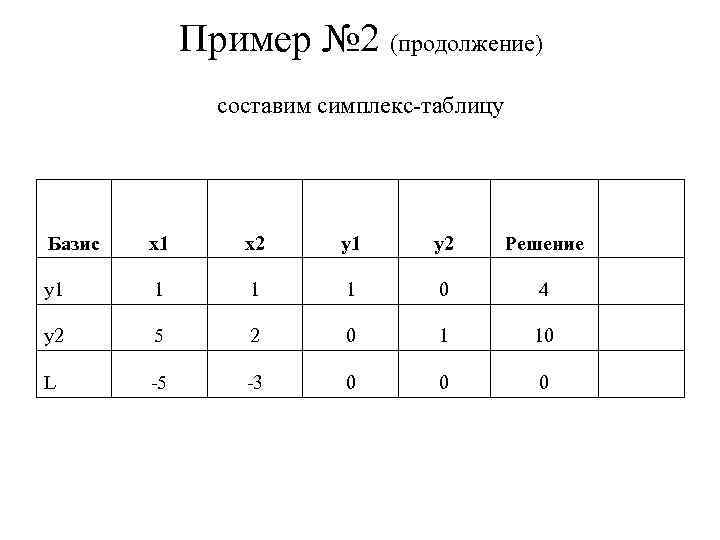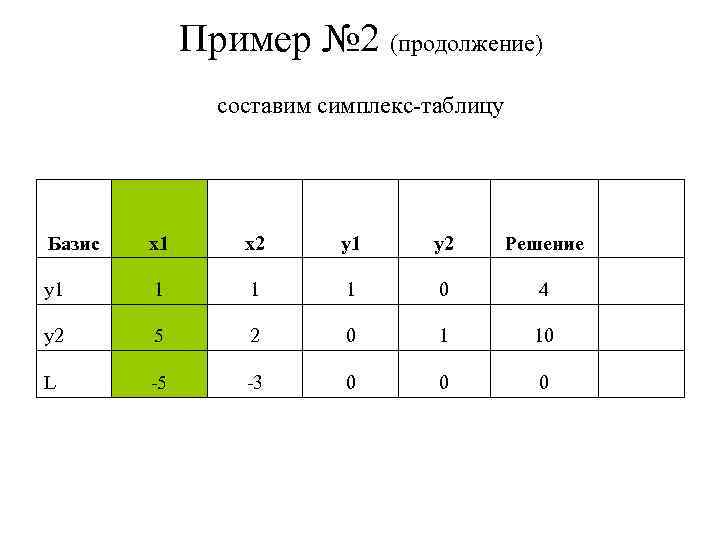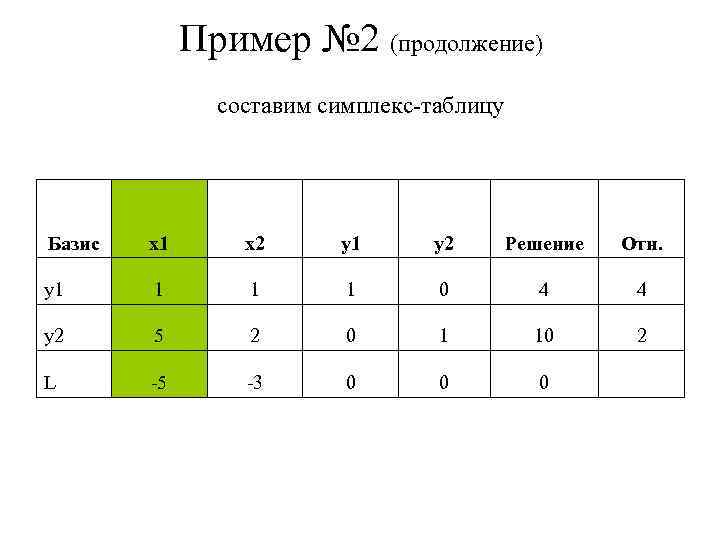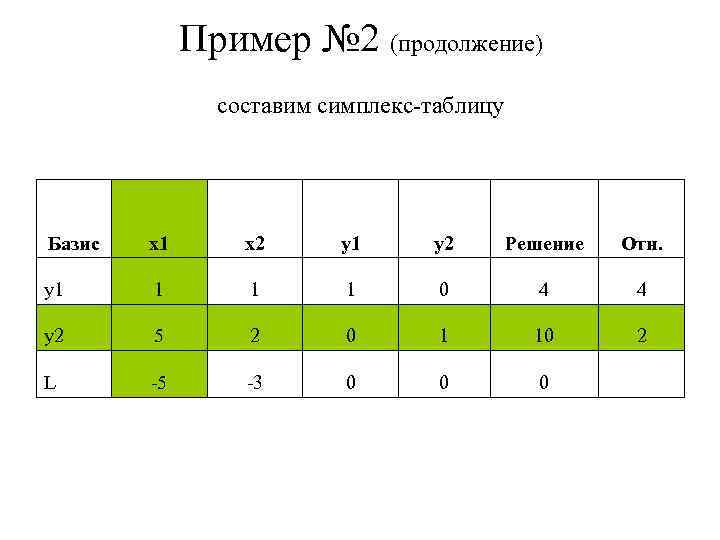Пример № 2 (продолжение) пересчитаем симплекс-таблицу Базис x 1 x 2 y 1 0 3/5 1 - 1/5 2 x 1 1 2/5 0 1/5 2 L 0 -1 0 y 2 1 Решение 10

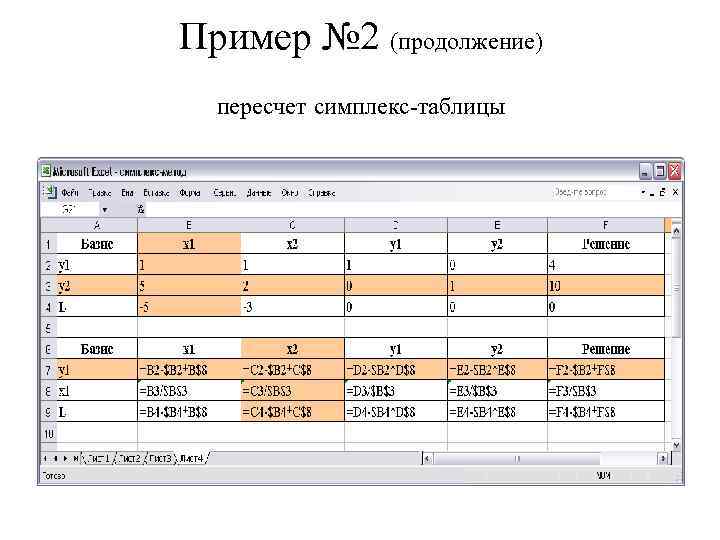Пример № 2 (продолжение) пересчет симплекс-таблицы

Пример № 2 (продолжение) симплекс-таблица № 2 Базис x 1 x 2 y 1 0 3/5 1 - 1/5 2 x 1 1 2/5 0 1/5 2 L 0 -1 0 y 2 1 Решение 10

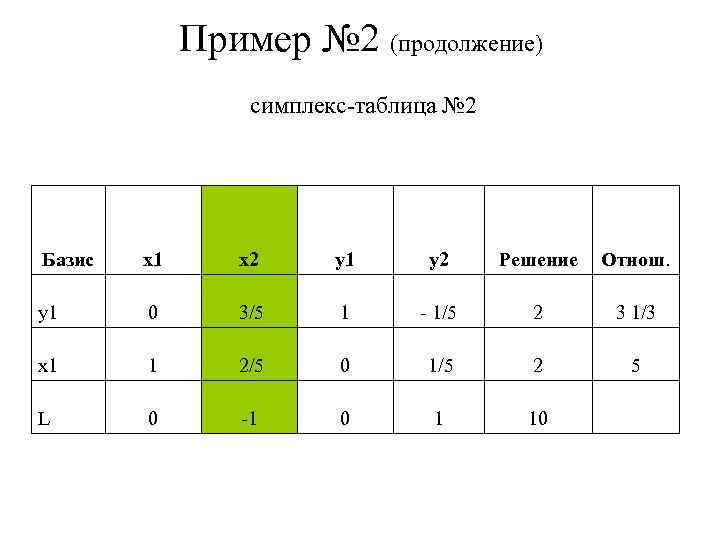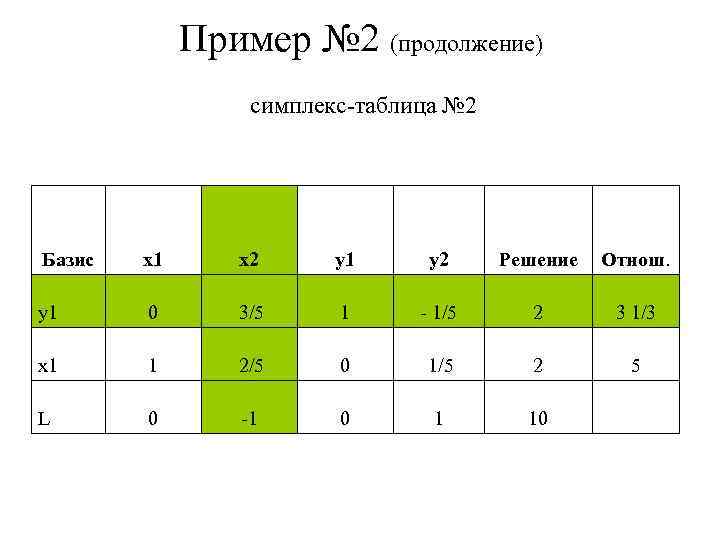Пример № 2 (продолжение) симплекс-таблица № 2 Базис x 1 x 2 y 1 0 3/5 1 - 1/5 2 3 1/3 x 1 1 2/5 0 1/5 2 5 L 0 -1 0 y 2 1 Решение 10 Отнош.

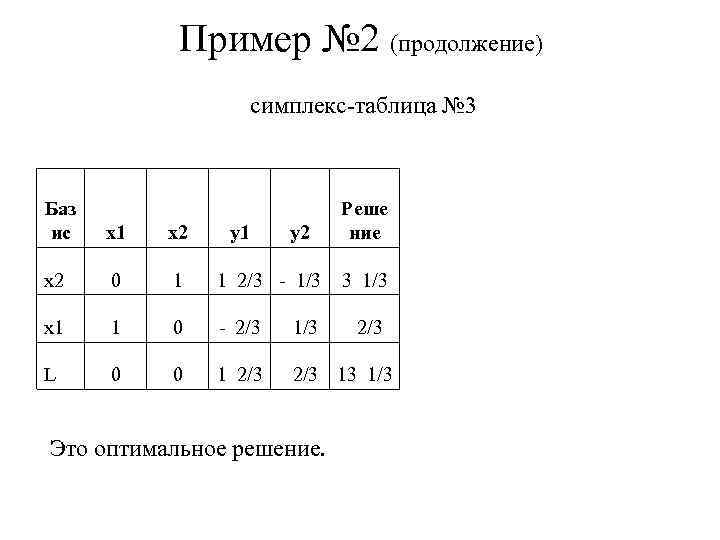Пример № 2 (продолжение) симплекс-таблица № 3 Баз ис x 1 x 2 0 1 1 2/3 - 1/3 3 1/3 x 1 1 0 - 2/3 1/3 L 0 0 1 2/3 13 1/3 y 1 y 2 Это оптимальное решение. Реше ние 2/3

Искусственное начальное решение В задачах линейного программирования, где все ограничения являются неравенствами типа "≤" (с неотрицательной правой частью), дополнительные (остаточные) переменные позволяют сформировать начальное допустимое базисное решение. В задачах ЛП, где есть ограничения в виде равенств или неравенств типа "≥" начальное допустимое базисное решение строится с использованием искусственных переменных. Эти переменные в первой итерации играют роль дополнительных остаточных переменных, но на последующих итерациях от них освобождаются. Разработано два тесно связанных между собой метода нахождения начального решения, которые используют искусственные переменные: М-метод и двухэтапный метод.

М-метод (метод больших штрафов) • • • Пусть задача ЛП записана в канонической форме. Для любого равенства i, в котором не содержится дополнительная остаточная переменная, введем искусственную переменную Ri, которая далее войдет в начальное базисное решение. Но, поскольку эта переменная искусственна (другими словами, не имеет никакого "физического смысла" в данной задаче), необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф. Переменная Ri, с помощью достаточно большого положительного числа М штрафуется путем ввода в целевую функцию выражения -MRi в случае максимизации целевой функции и выражения +MRi — в случае минимизации. Вследствие этого штрафа естественно предположить, что процесс оптимизации симплекс-метода приведет к нулевому значению переменной Ri. Использование штрафа М может и не привести к исключению искусственной переменной в конечной симплекс-итерации. Если исходная задача линейного программирования не имеет допустимого решения (например, система ограничений несовместна), тогда в конечной симплекс-итерации по крайней мере одна искусственная переменная будет иметь положительное значение. Это является признаком того, что задача не имеет допустимого решения.

М-метод (продолжение) Начальный базис в этой задаче – R 1, R 2, y 2

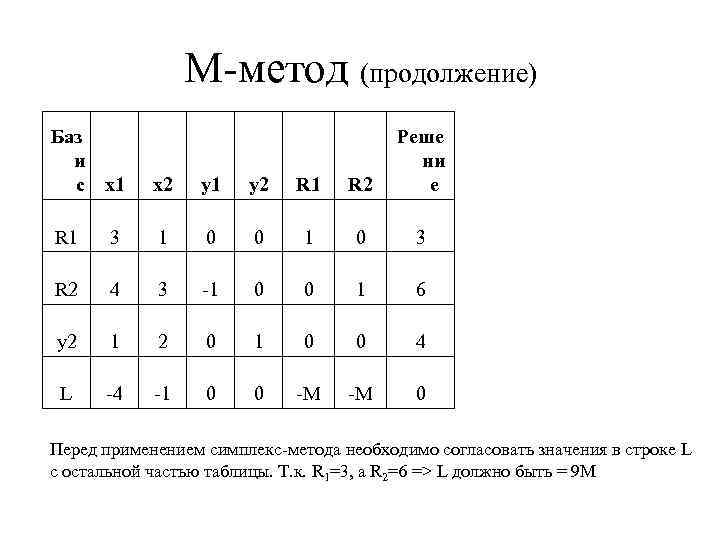М-метод (продолжение) Баз и с x 1 x 2 y 1 y 2 R 1 R 2 Реше ни е R 1 3 1 0 0 1 0 3 R 2 4 3 -1 0 0 1 6 y 2 1 2 0 1 0 0 4 L -4 -1 0 0 -M -M 0 Перед применением симплекс-метода необходимо согласовать значения в строке L с остальной частью таблицы. Т. к. R 1=3, а R 2=6 => L должно быть = 9 M

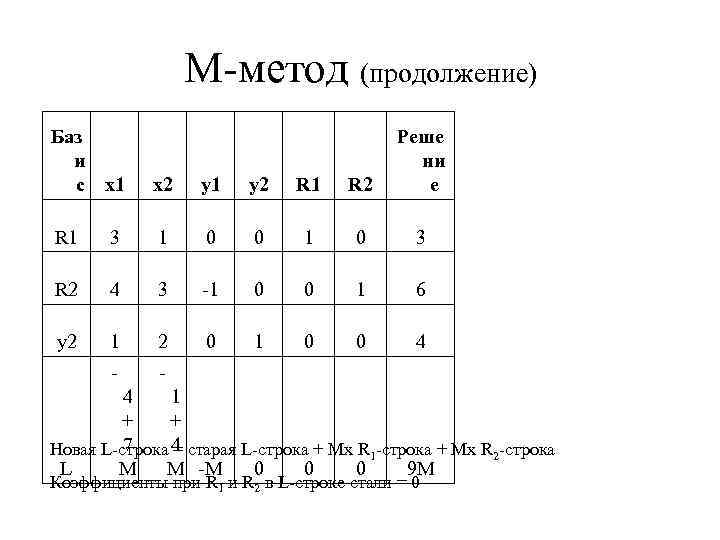М-метод (продолжение) Баз и с x 1 x 2 y 1 y 2 R 1 R 2 Реше ни е R 1 3 1 0 0 1 0 3 R 2 4 3 -1 0 0 1 6 y 2 1 2 0 1 0 0 4 - - 4 1 + + 7 4 Новая L-строка = старая L-строка + Мх R 1 -строка + Мх R 2 -строка L M M -M 0 0 0 9 M Коэффициенты при R 1 и R 2 в L-строке стали = 0

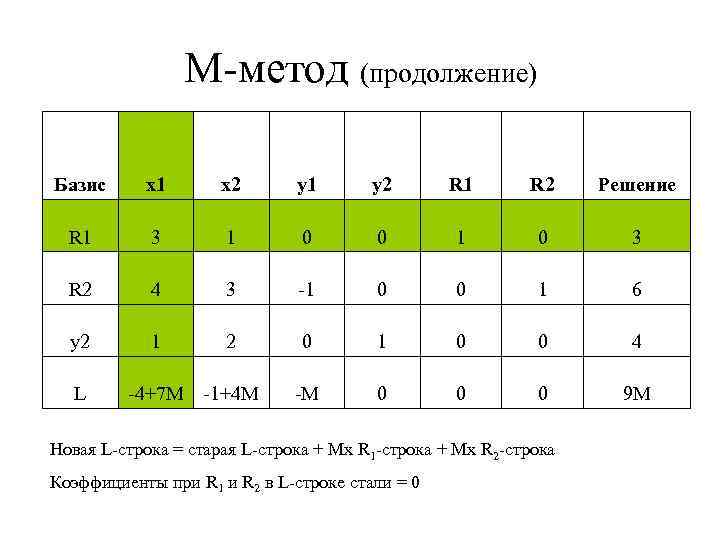М-метод (продолжение) Базис x 1 x 2 y 1 y 2 R 1 R 2 Решение R 1 3 1 0 0 1 0 3 R 2 4 3 -1 0 0 1 6 y 2 1 2 0 1 0 0 4 -M 0 0 0 9 M L -4+7 M -1+4 M Новая L-строка = старая L-строка + Мх R 1 -строка + Мх R 2 -строка Коэффициенты при R 1 и R 2 в L-строке стали = 0

Двухэтапный метод Позволяет избежать ошибок округления, свойственных M-методу. Состоит из 2 -х этапов: Этап 1 – поиск начального допустимого решения; Этап 2 – решение задачи, т. е. поиск оптимального решения.

Двухэтапный метод (продолжение) Этап 1. Задача ЛП записывается в канонической форме, а в ограничения добавляются необходимые искусственные переменные (как и в Мметоде) для получения начального базисного решения. Решается задача ЛП минимизации суммы искусственных переменных с исходными ограничениями (W=R 1+R 2+…+Rk min). Если минимальное значение этой новой целевой функции больше нуля, значит, исходная задача не имеет допустимого решения, и процесс вычислений заканчивается. Положительные значения искусственных переменных указывают на то, что исходная система ограничений несовместна. Если новая целевая функция равна нулю, переходим ко второму этапу. Этап 2. Оптимальное базисное решение, полученное на первом этапе, используется как начальное допустимое базисное решение исходной задачи.

Двухэтапный метод. Пример Переход к канонической форме. Добавление искусственных переменных

Двухэтапный метод. Пример

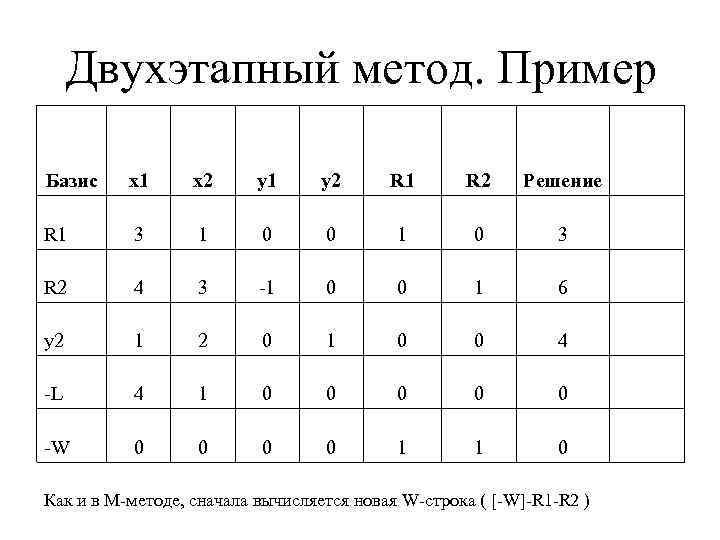Двухэтапный метод. Пример Базис x 1 x 2 y 1 y 2 R 1 R 2 Решение R 1 3 1 0 0 1 0 3 R 2 4 3 -1 0 0 1 6 y 2 1 2 0 1 0 0 4 -L 4 1 0 0 0 -W 0 0 1 1 0 Как и в М-методе, сначала вычисляется новая W-строка ( [-W]-R 1 -R 2 )

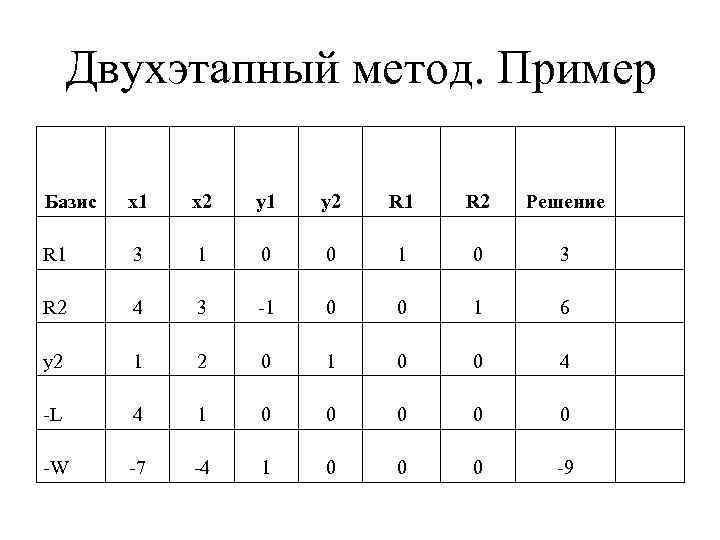Двухэтапный метод. Пример Базис x 1 x 2 y 1 y 2 R 1 R 2 Решение R 1 3 1 0 0 1 0 3 R 2 4 3 -1 0 0 1 6 y 2 1 2 0 1 0 0 4 -L 4 1 0 0 0 -W -7 -4 1 0 0 0 -9

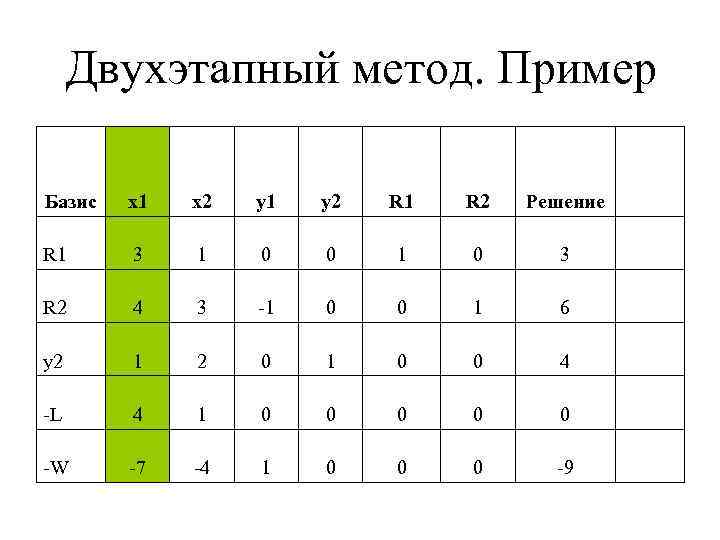Двухэтапный метод. Пример Базис x 1 x 2 y 1 y 2 R 1 R 2 Решение Отн. R 1 3 1 0 0 1 0 3 1 R 2 4 3 -1 0 0 1 6 1, 5 y 2 1 2 0 1 0 0 4 4 -L 4 1 0 0 0 -W -7 -4 1 0 0 0 -9

Двухэтапный метод. Пример Базис x 1 x 2 y 1 y 2 R 1 R 2 Решение x 1 1 0, 3333 0 0 0, 33333 0 1, 33333 1 2 1 0, 33333 0 -4 0 -2 R 2 y 2 0 0 1, 6667 -1 0 -L 0 -0, 333 0 0 1, 33333 -W 0 -1, 667 1 0 2, 33333

Двухэтапный метод. Пример Базис x 1 x 2 y 1 y 2 R 1 R 2 Решение Отн. x 1 1 0, 3333 0 0 0, 33333 0 1, 33333 1 2 1, 2 1 0, 33333 0 3 1, 8 0 -4 0 -2 R 2 y 2 0 0 1, 6667 -1 0 -L 0 -0, 333 0 0 1, 33333 -W 0 -1, 667 1 0 2, 33333

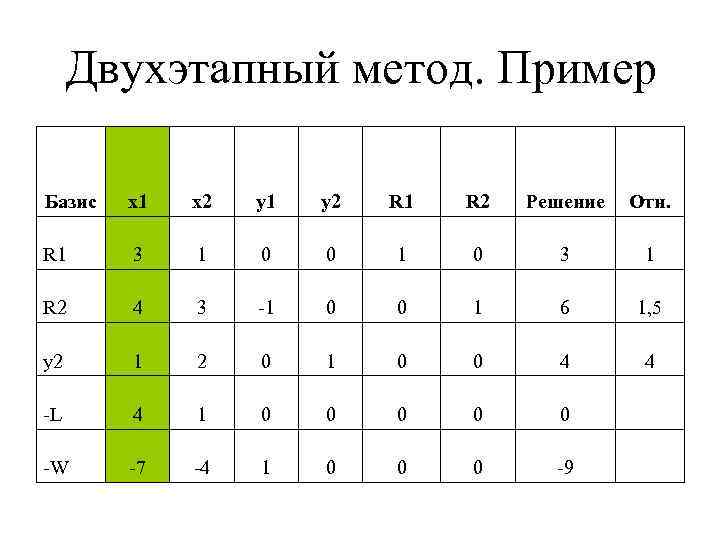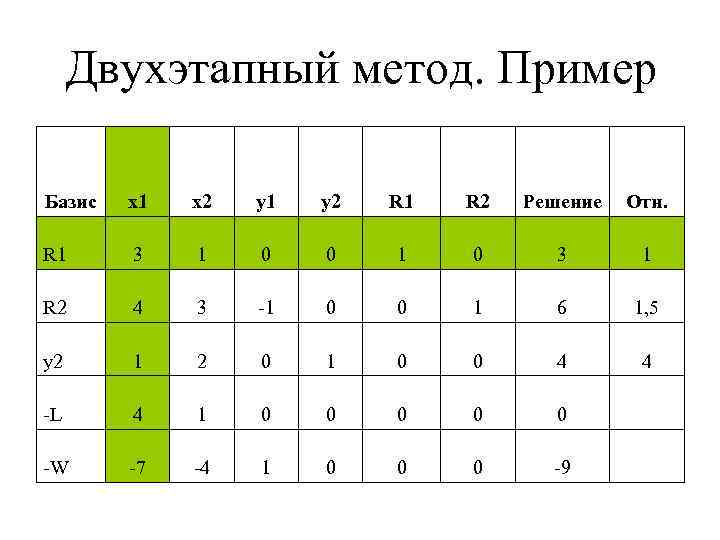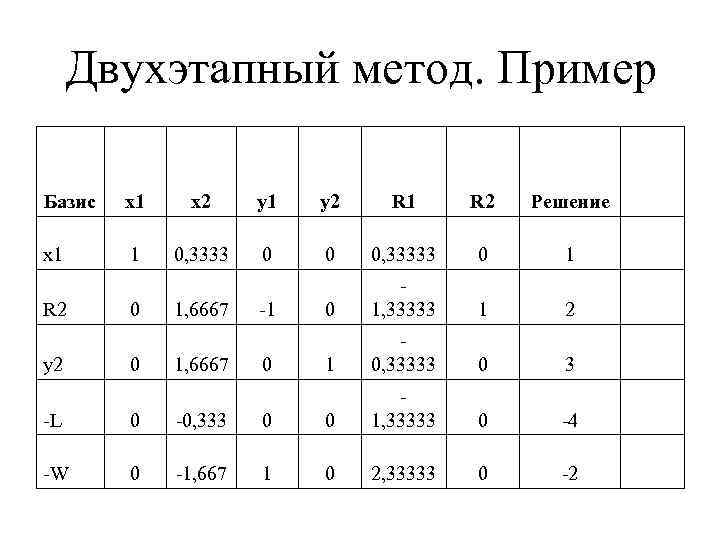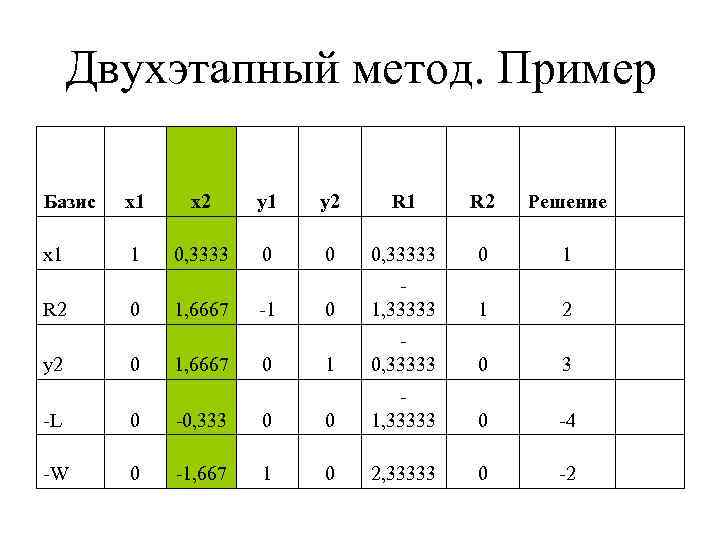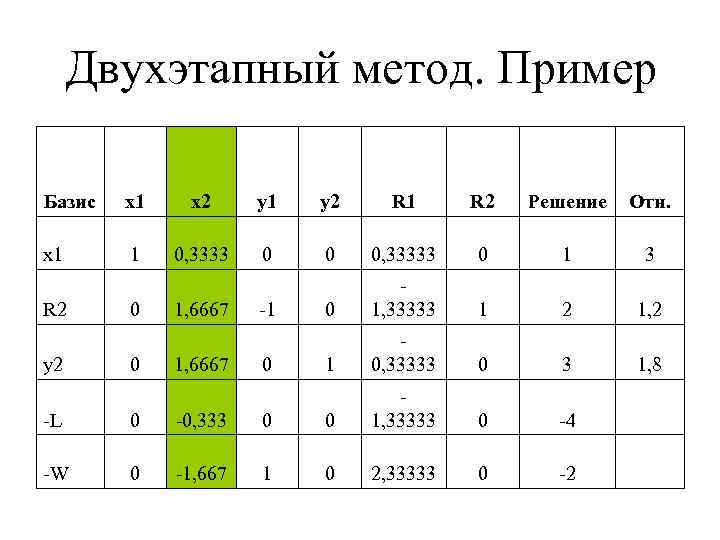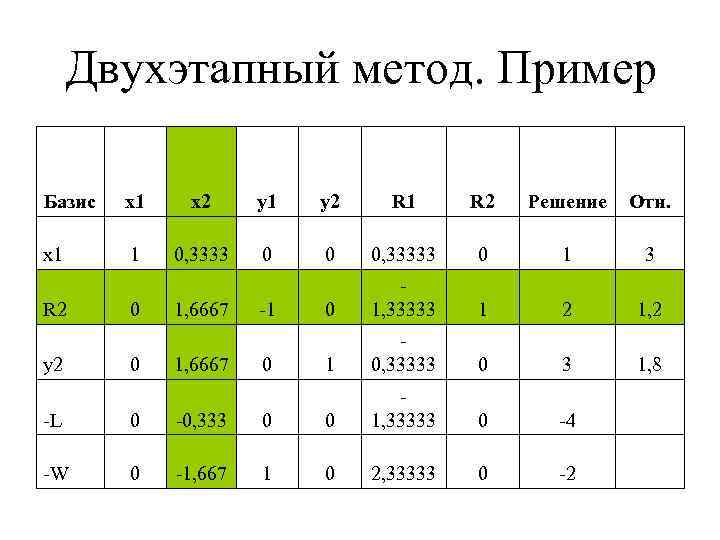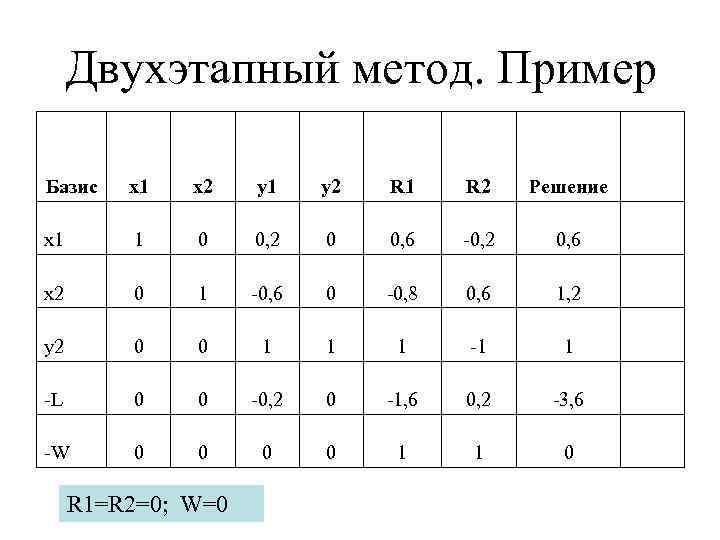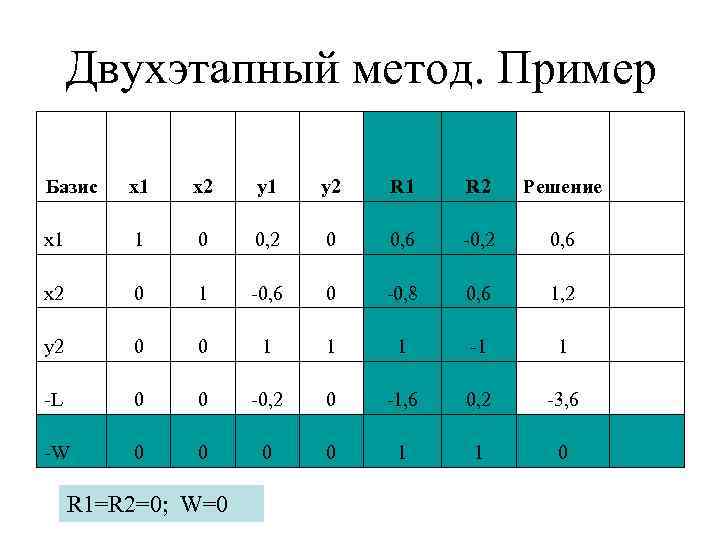Двухэтапный метод. Пример Базис x 1 x 2 y 1 y 2 R 1 R 2 Решение x 1 1 0 0, 2 0 0, 6 -0, 2 0, 6 x 2 0 1 -0, 6 0 -0, 8 0, 6 1, 2 y 2 0 0 1 1 1 -L 0 0 -0, 2 0 -1, 6 0, 2 -3, 6 -W 0 0 1 1 0 R 1=R 2=0; W=0

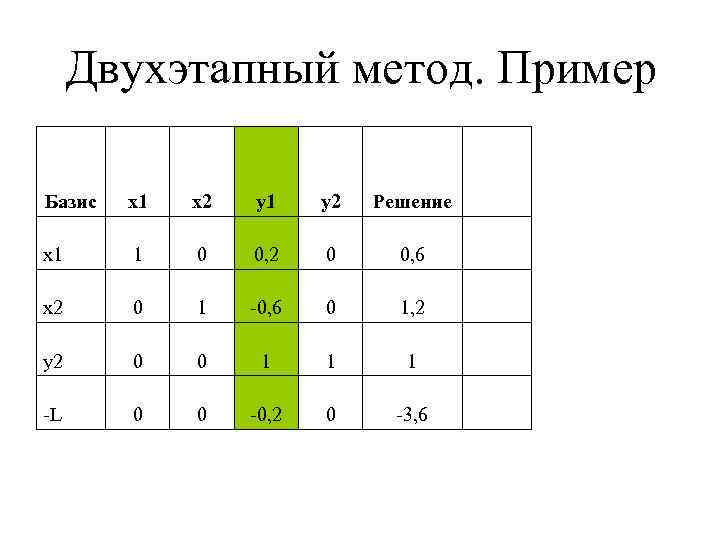Двухэтапный метод. Пример Базис x 1 x 2 y 1 y 2 Решение x 1 1 0 0, 2 0 0, 6 x 2 0 1 -0, 6 0 1, 2 y 2 0 0 1 1 1 -L 0 0 -0, 2 0 -3, 6

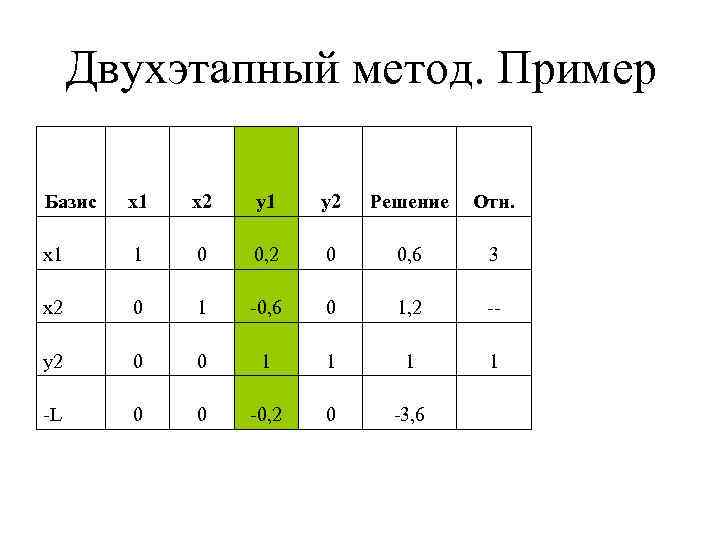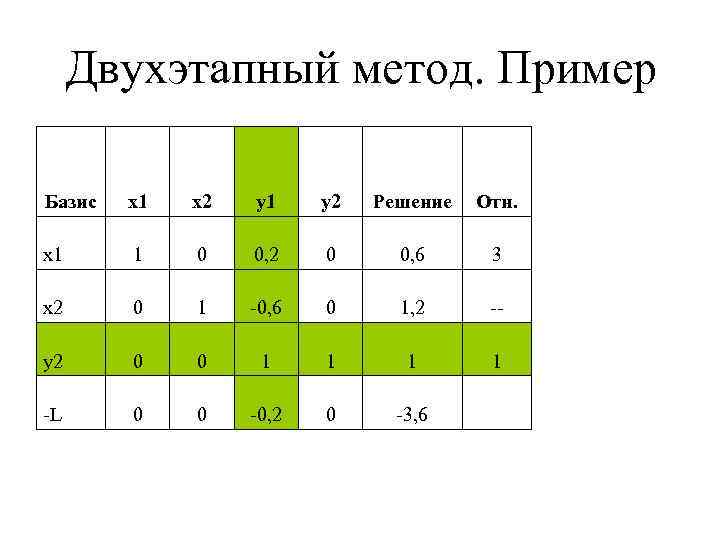Двухэтапный метод. Пример Базис x 1 x 2 y 1 y 2 Решение Отн. x 1 1 0 0, 2 0 0, 6 3 x 2 0 1 -0, 6 0 1, 2 -- y 2 0 0 1 1 -L 0 0 -0, 2 0 -3, 6

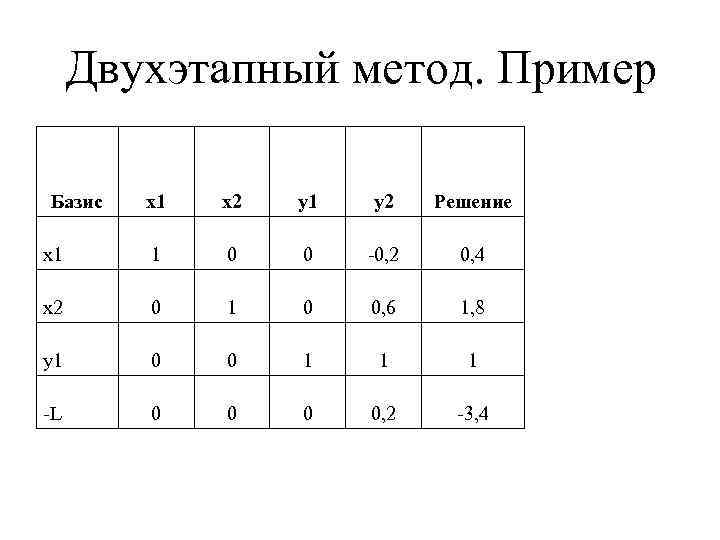Двухэтапный метод. Пример Базис x 1 x 2 y 1 y 2 Решение x 1 1 0 0 -0, 2 0, 4 x 2 0 1 0 0, 6 1, 8 y 1 0 0 1 1 1 -L 0 0, 2 -3, 4

Решение ЗЛП в Math. Cad

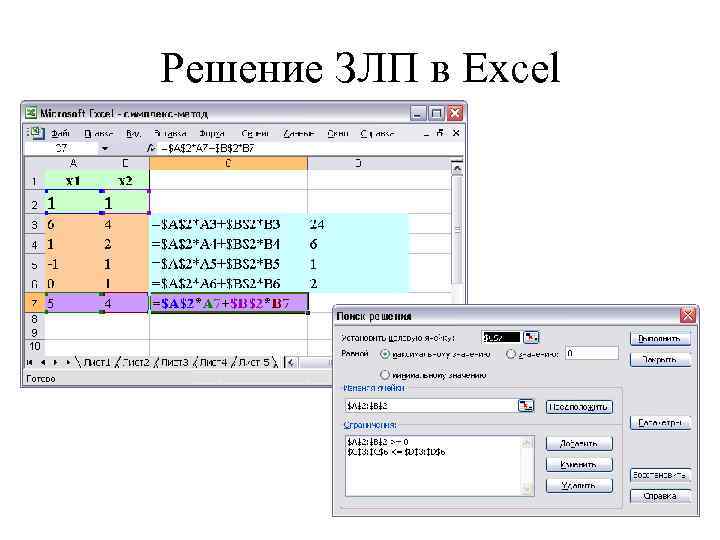
Решение ЗЛП в Excel

Альтернативный оптимум (множество оптимальных решений)

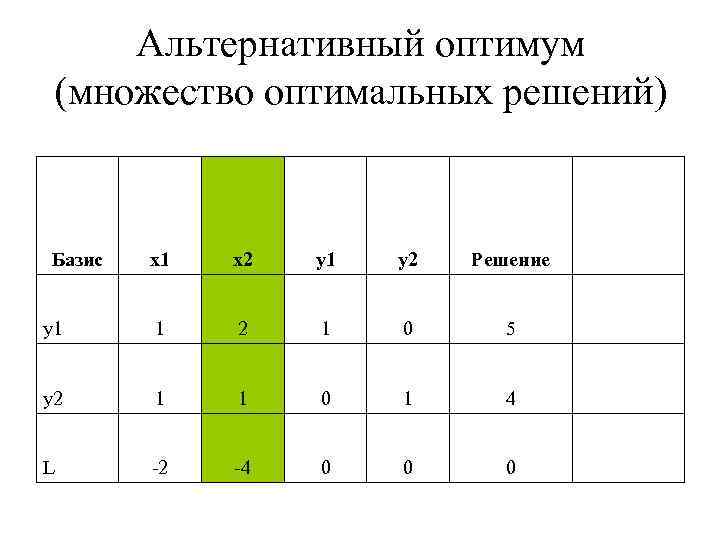Альтернативный оптимум (множество оптимальных решений) Базис x 1 x 2 y 1 y 2 Решение y 1 1 2 1 0 5 y 2 1 1 0 1 4 L -2 -4 0 0 0

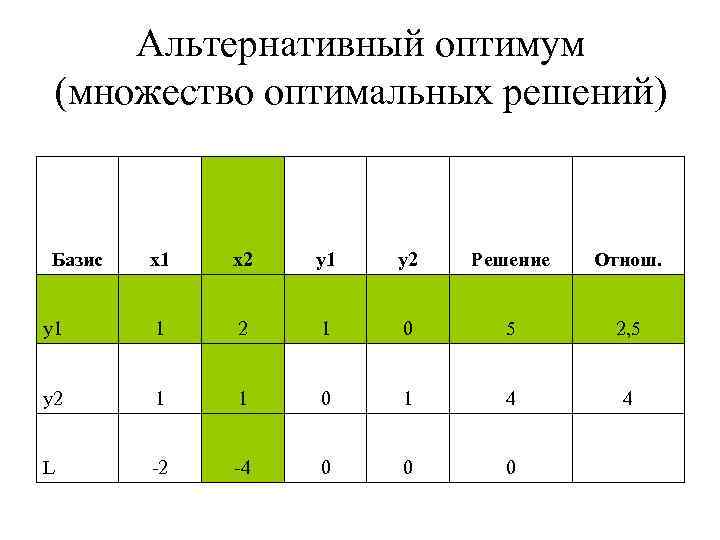Альтернативный оптимум (множество оптимальных решений) Базис x 1 x 2 y 1 y 2 Решение Отнош. y 1 1 2 1 0 5 2, 5 y 2 1 1 0 1 4 4 L -2 -4 0 0 0

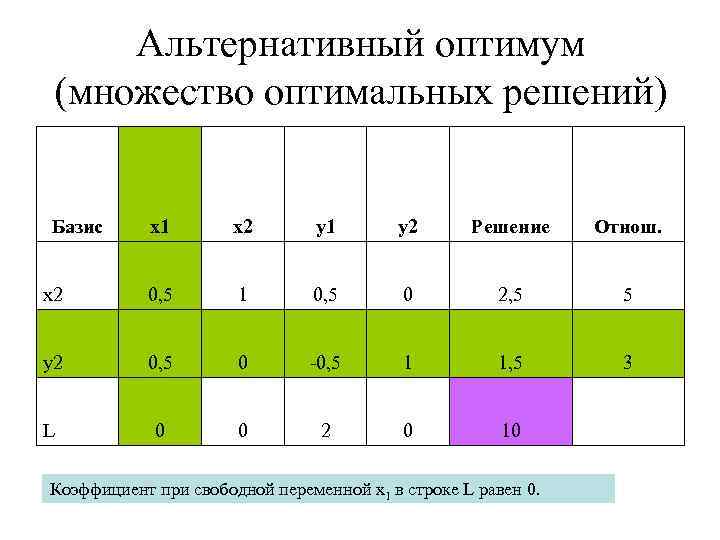Альтернативный оптимум (множество оптимальных решений) Базис x 1 x 2 y 1 y 2 Решение Отнош. x 2 0, 5 1 0, 5 0 2, 5 5 y 2 0, 5 0 -0, 5 1 1, 5 3 L 0 0 2 0 10 Коэффициент при свободной переменной x 1 в строке L равен 0.

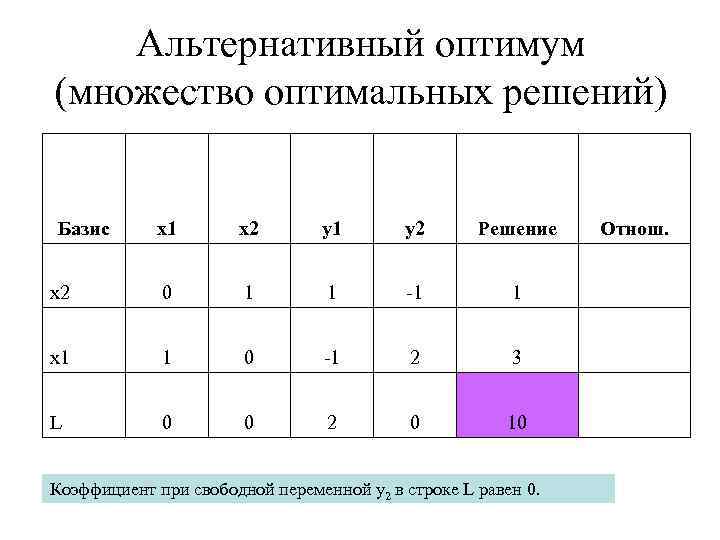Альтернативный оптимум (множество оптимальных решений) Базис x 1 x 2 y 1 y 2 Решение Отнош. x 2 0 1 1 -1 1 x 1 1 0 -1 2 3 L 0 0 2 0 10 Коэффициент при свободной переменной y 2 в строке L равен 0.

Отсутствие оптимального решения (неограниченность целевой функции)

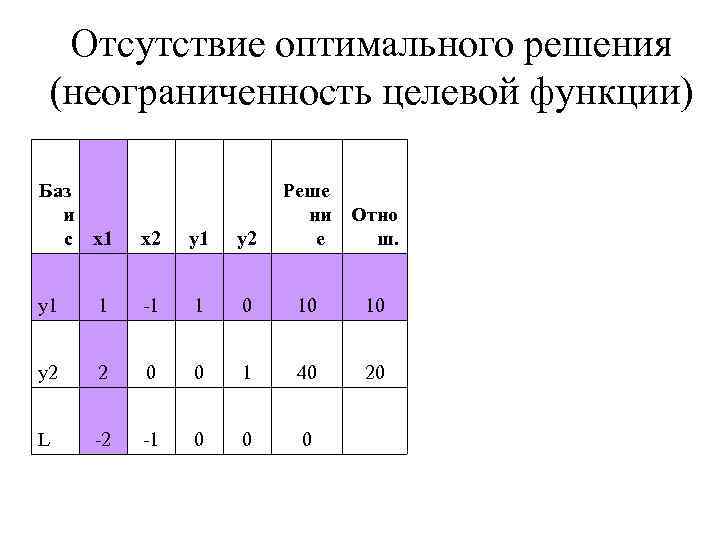Отсутствие оптимального решения (неограниченность целевой функции) Баз и с x 1 Реше ни Отно ш. е x 2 y 1 y 2 y 1 1 -1 1 0 10 10 y 2 2 0 0 1 40 20 L -2 -1 0 0 0

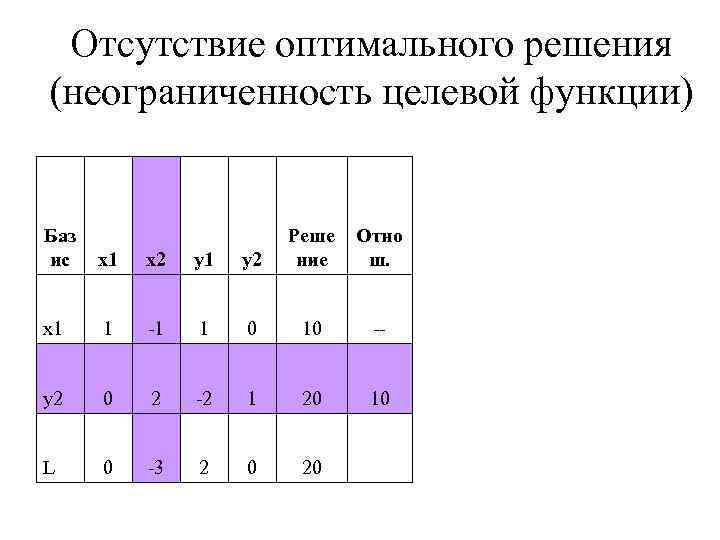Отсутствие оптимального решения (неограниченность целевой функции) Баз ис y 2 Реше ние Отно ш. x 1 x 2 y 1 x 1 1 -1 1 0 10 -- y 2 0 2 -2 1 20 10 L 0 -3 2 0 20

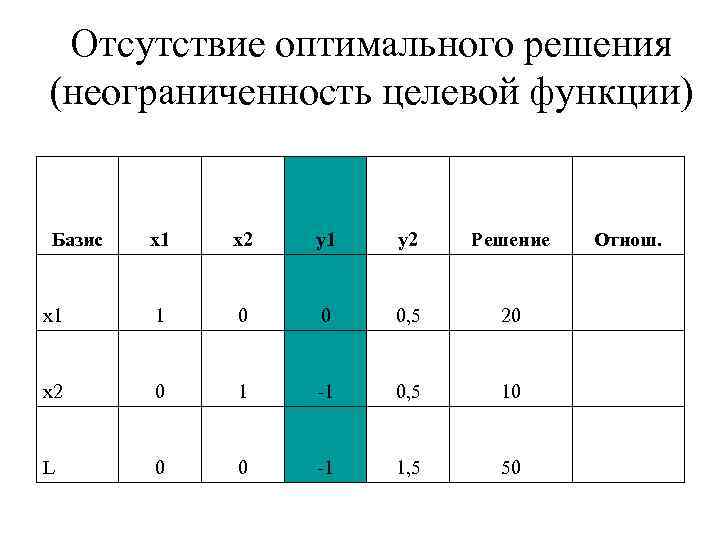Отсутствие оптимального решения (неограниченность целевой функции) Базис x 1 x 2 y 1 y 2 Решение Отнош. x 1 1 0 0 0, 5 20 x 2 0 1 -1 0, 5 10 L 0 0 -1 1, 5 50

Вырожденность В ходе выполнения симплекс-метода проверка условия допустимости может привести к неоднозначному выбору исключаемой из базиса переменной. В этом случае на следующей итерации одна или несколько базисных переменных примут нулевое значение. Тогда новое решение будет вырожденным. Решение может быть только временно вырожденным. Поэтому, несмотря на то, что оптимальное решение не достигнуто, остановить вычисления когда впервые обнаруживается вырожденность нельзя. Вырожденность может привести к зацикливанию, когда при реализации симплекс-метода некоторая последовательность будет повторяться, не изменяя значения целевой функции и не приводя к завершению вычислительного процесса.

Вырожденность (продолжение)

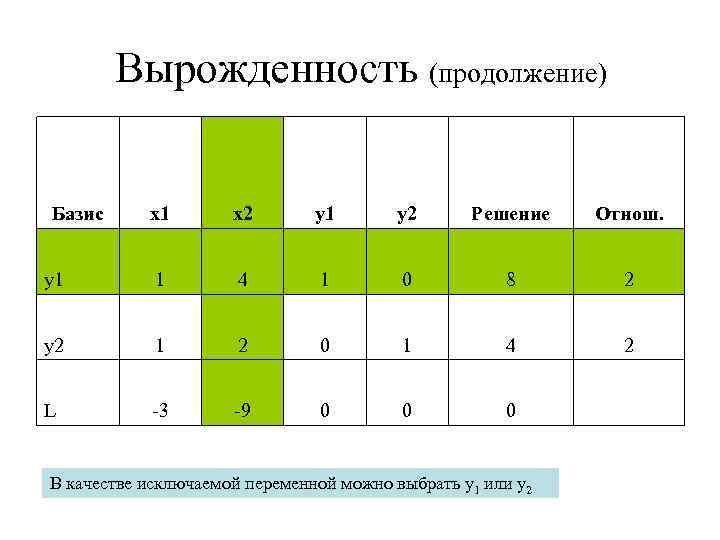Вырожденность (продолжение) Базис x 1 x 2 y 1 y 2 Решение Отнош. y 1 1 4 1 0 8 2 y 2 1 2 0 1 4 2 L -3 -9 0 0 0 В качестве исключаемой переменной можно выбрать y 1 или y 2

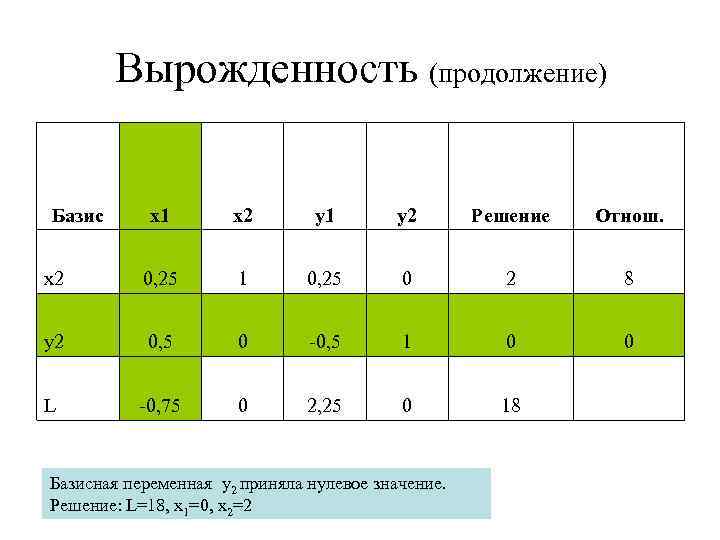Вырожденность (продолжение) Базис x 1 x 2 y 1 y 2 Решение Отнош. x 2 0, 25 1 0, 25 0 2 8 y 2 0, 5 0 -0, 5 1 0 0 L -0, 75 0 2, 25 0 18 Базисная переменная y 2 приняла нулевое значение. Решение: L=18, x 1=0, x 2=2

Вырожденность (продолжение) Баз ис x 1 x 2 y 1 x 2 0 1 0, 5 -0, 5 2 x 1 1 0 -1 2 0 L 0 0 1, 5 18 y 2 Решен Отно ие ш. Базисная переменная x 1 приняла нулевое значение. Решение: L=18, x 1=0, x 2=2

Лабораторная работа № 1. Решение задач линейного программирования 1. Решить графически и методом симплекс таблиц задачу линейного программирования. В задаче нужно найти максимум и минимум заданной целевой функции. 2. Сформулировать двойственные задачи линейного программирования и решить их симплекс-методом.