СИЛОВОЙ РАСЧЁТ МЕХАНИЗМОВ, СОДЕРЖАЩИХ ВЫСШИЕ

СИЛОВОЙ РАСЧЁТ МЕХАНИЗМОВ, СОДЕРЖАЩИХ ВЫСШИЕ КИНЕМАТИЧЕСКИЕ ПАРЫ Пример 1. Расчёт плоского кулачкового механизма. 6 неизвестных: R 01 x и R 01 y R 02 и М 02 z. R R 12 n= – R 21 n обобщённая движущая сила Q. – угол давления – угол между направлением силы и скоростью точки приложения силы 6 уравнений кинетостатики: R 01 x + Ф 1 cos t + R 12 n sin = 0, R 02 – R 12 n sin = 0, R 01 y + Ф 1 sin t – R 12 n cos – G 1 = 0, R 12 ncos – Pпр – Ф 2 – G 2 = 0, Q – R 12 n e cos – R 12 n sin (h 0 + s) – G 1 sin t + M 10(Ф) ,

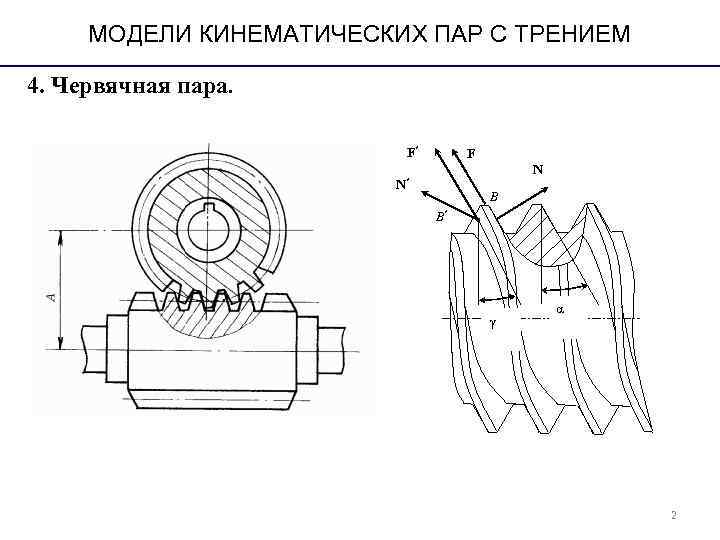
МОДЕЛИ КИНЕМАТИЧЕСКИХ ПАР С ТРЕНИЕМ 4. Червячная пара. F′ F N′ B B′ α γ 2

МОДЕЛИ КИНЕМАТИЧЕСКИХ ПАР С ТРЕНИЕМ 4. Червячная пара. F′ F z z* N N′ z** B B′ F N y** α y* α B y γ x* x** x Угол γ – угол подъёма винтовой линии червяка (при γ = 0 винтовая линия обращается в кольцевую). Угол α – угол профиля исходного контура (при α = 0 виток червяка становится прямобочным). 3

МОДЕЛИ КИНЕМАТИЧЕСКИХ ПАР С ТРЕНИЕМ 4. Червячная пара. F′ F z, z* N z, z* N′ z** N y** B z** B′ F y** P N T F α y* α B y γ B γ S y γ x*, x** x S = N cosα cosγ – F sinγ =N(cosα cosγ – f sign. N sinγ sign), P = N cosα sinγ + F cosγ =N(cosα sinγ + f sign. N cosγ sign), T = N sinα. S – осевая сила на червяке; P – окружная сила на червяке; Т – радиальная сила. 4

МОДЕЛИ КИНЕМАТИЧЕСКИХ ПАР С ТРЕНИЕМ 5. Винтовая пара. y* y d. S d. N v d. T z А x d. P z* d. F x* Ось Ay* направлена перпендикулярно винтовой поверхности, Ось Ax* – по касательной к винтовой поверхности, Ось Az* – так, чтобы получилась правая система координат. d. N направлена вдоль оси Ay*, d. F – вдоль оси Ax*. 5

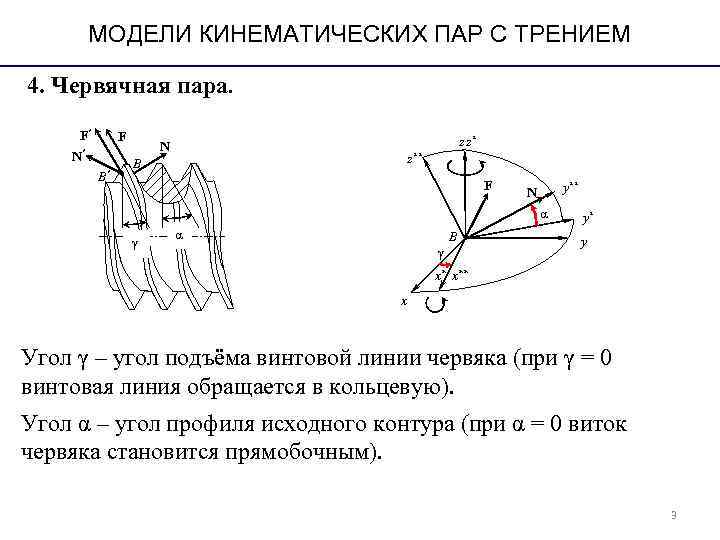
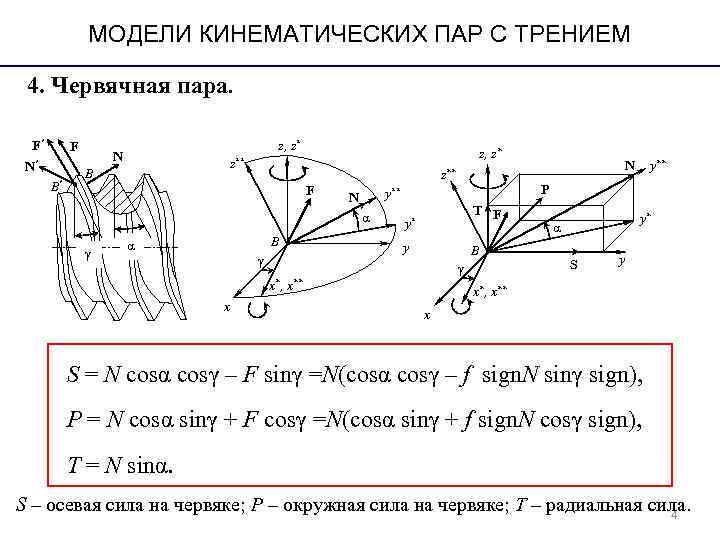
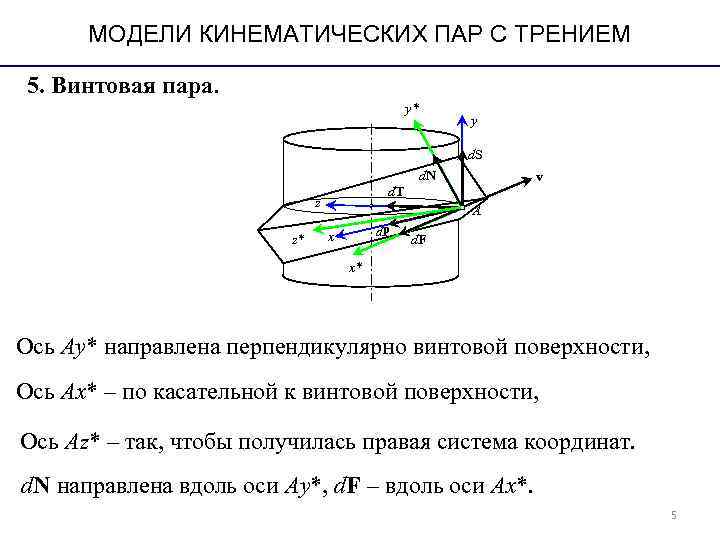
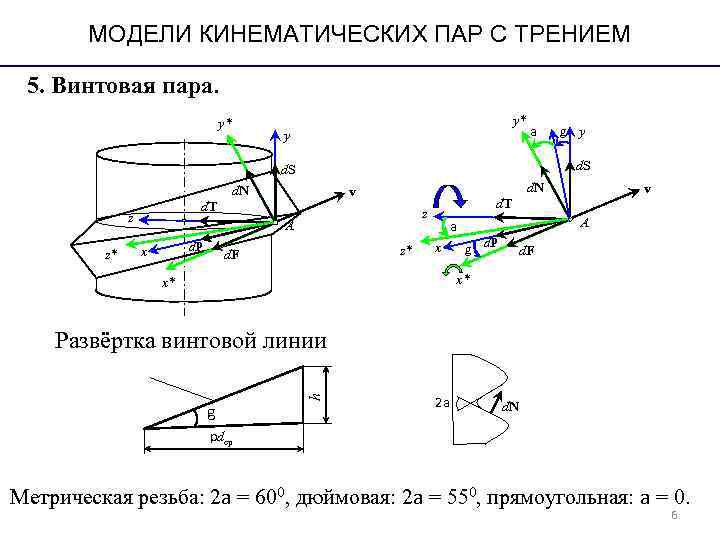
МОДЕЛИ КИНЕМАТИЧЕСКИХ ПАР С ТРЕНИЕМ 5. Винтовая пара. y* y a g y d. S d. N v d. N v d. T z А a А z* x d. P d. F z* x g d. P d. F x* Развёртка винтовой линии h 2 a d. N g pdср Метрическая резьба: 2 a = 600, дюймовая: 2 a = 550, прямоугольная: a = 0. 6

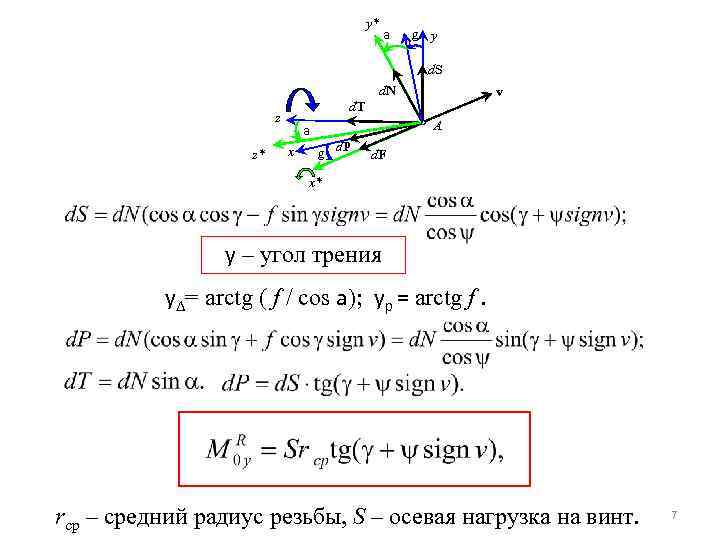
y* a g y d. S d. N v d. T z a А z* x g d. P d. F x* y – угол трения y = arctg ( f / cos a); yр = arctg f. rср – средний радиус резьбы, S – осевая нагрузка на винт. 7

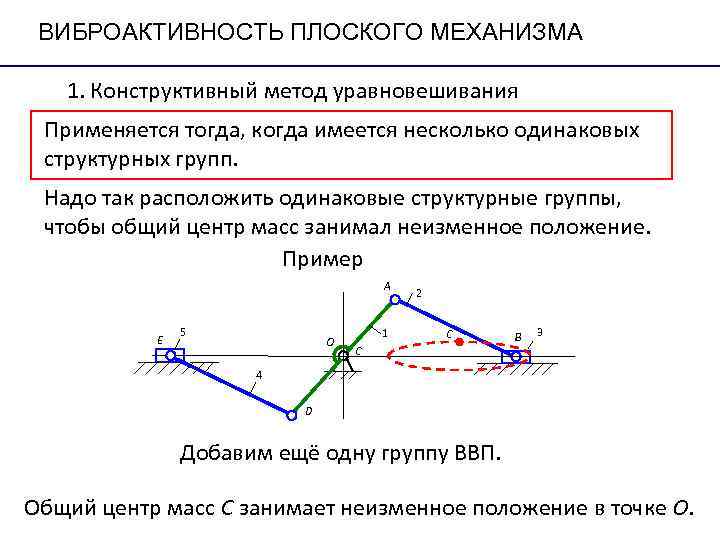
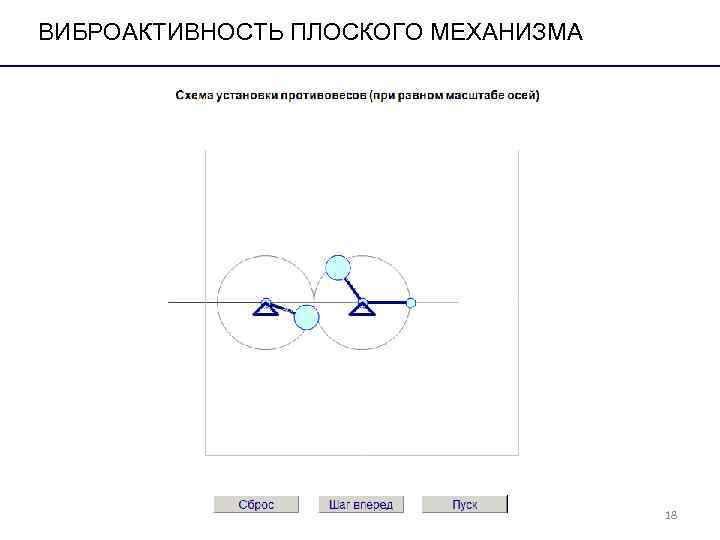
ВИБРОАКТИВНОСТЬ ПЛОСКОГО МЕХАНИЗМА 1. Конструктивный метод уравновешивания Применяется тогда, когда имеется несколько одинаковых структурных групп. Надо так расположить одинаковые структурные группы, чтобы общий центр масс занимал неизменное положение. Пример A 2 5 1 С B 3 E O С 4 D Добавим ещё одну группу ВВП. Общий центр масс С занимает неизменное положение в точке О.

ВИБРОАКТИВНОСТЬ ПЛОСКОГО МЕХАНИЗМА 1. Конструктивный метод уравновешивания Пример 1: оппозитный двигатель Оппозитный двигатель: цилиндры расположены по обе стороны коленчатого вала с углом развала 180 градусов. Преимущества: – низкий центр масс, – снижена внешняя виброактивность за счёт конструкционного метода уравновешивания. 9

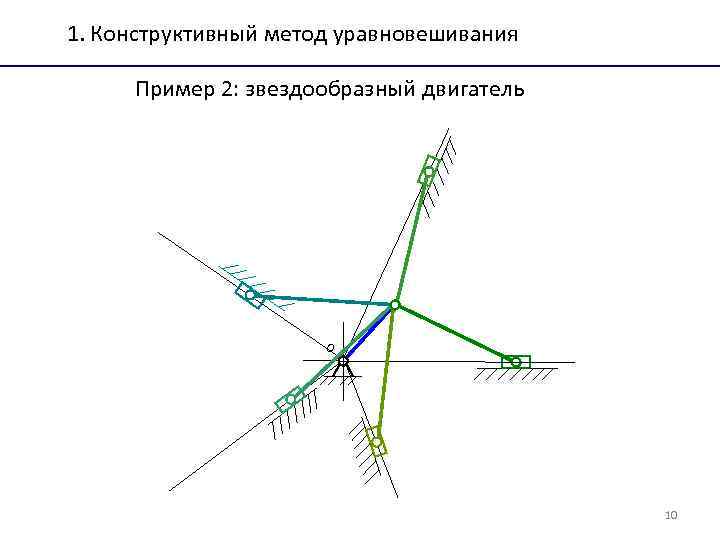
1. Конструктивный метод уравновешивания Пример 2: звездообразный двигатель O 10

1. Конструктивный метод уравновешивания Пример 2: звездообразный двигатель 5 -цилиндровый 9 -цилиндровый двигатель авиамотор с планетарным редуктором 11

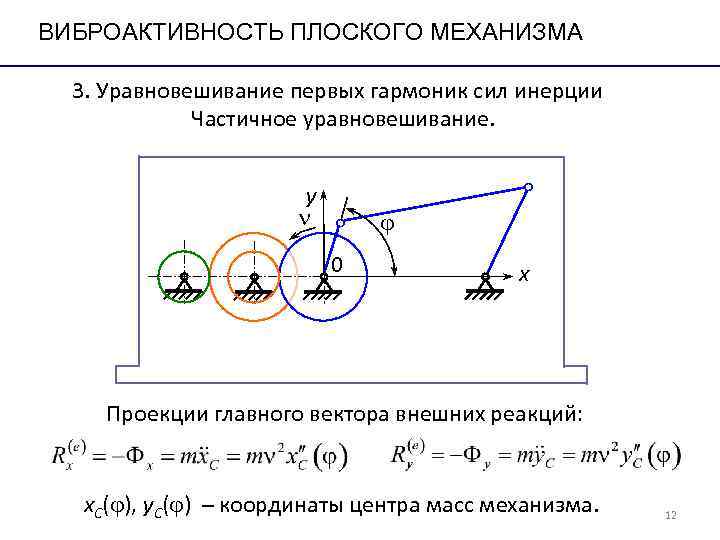
ВИБРОАКТИВНОСТЬ ПЛОСКОГО МЕХАНИЗМА 3. Уравновешивание первых гармоник сил инерции Частичное уравновешивание. y n j 0 х Проекции главного вектора внешних реакций: х. С(j), y. C(j) – координаты центра масс механизма. 12

ВИБРОАКТИВНОСТЬ ПЛОСКОГО МЕХАНИЗМА 3. Уравновешивание первых гармоник сил инерции y n j –n q+ q– 01 х m+ m– Разложим х. С (j), y. C (j) в ряд Фурье: Установим два вращающихся противовеса m+ и m– так, чтобы:

ВИБРОАКТИВНОСТЬ ПЛОСКОГО МЕХАНИЗМА 3. Уравновешивание первых гармоник сил инерции Приравняем коэффициенты при cos (j) и sin (j): (1) (2) (3) (4) 14

ВИБРОАКТИВНОСТЬ ПЛОСКОГО МЕХАНИЗМА 3. Уравновешивание первых гармоник сил инерции Первый противовес: масса m+, радиус r+ и угол установки q+ (1) + (4): (3) – (2): Второй противовес: масса m–, радиус r– и угол установки q– (1) – (4): (3) + (2): 15

ВИБРОАКТИВНОСТЬ ПЛОСКОГО МЕХАНИЗМА 3. Уравновешивание первых гармоник сил инерции y q+ q– 0 01 х r+ r– m+ m– Задаваясь радиусом установки противовесов r+ и r–, определяют параметры противовесов: m+, q+, m–, q–. 16

ВИБРОАКТИВНОСТЬ ПЛОСКОГО МЕХАНИЗМА 17

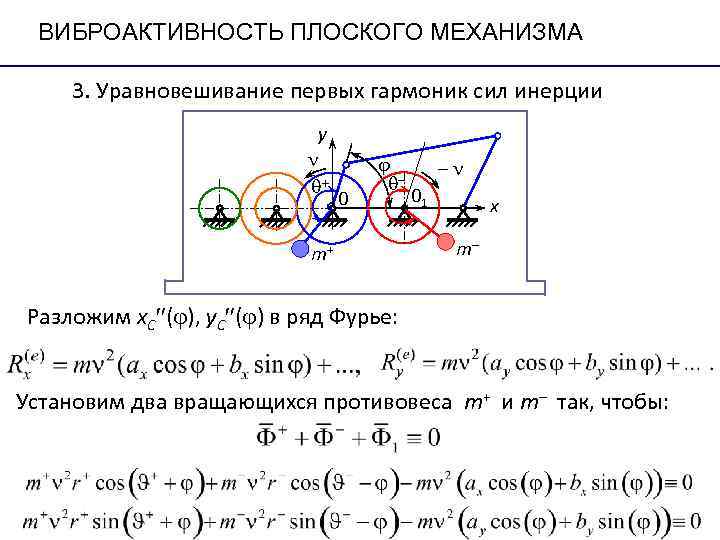
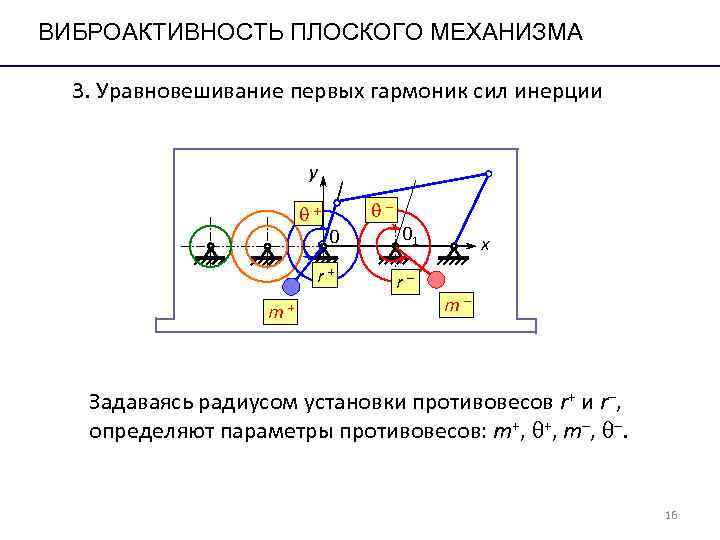
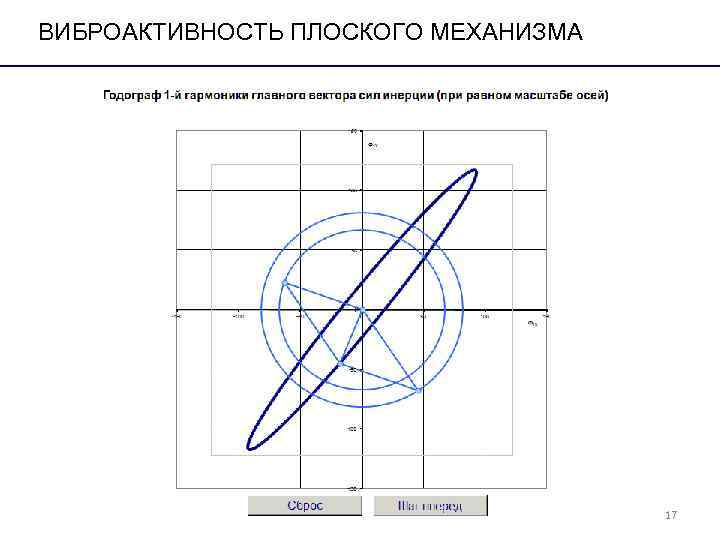
ВИБРОАКТИВНОСТЬ ПЛОСКОГО МЕХАНИЗМА 18

МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЕЙ Электродвигатель постоянного тока с независимым возбуждением ь Закон электромагнитной индукции Е (ЭДС) – обратная электродвижущая сила k. E – коэффициент пропорциональности ь Уравнение электрической цепи ь Закон Ампера R – активное сопротивление [Ом] Q – движущий момент L – индуктивность [Гн] k. M – коэффициент пропорциональности

МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЕЙ Электродвигатель постоянного тока с независимым возбуждением Уравнение электрической цепи Потери в цепи ротора 1. Идеальная характеристика двигателя Все потери равны нулю: Тогда: 20

МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЕЙ Электродвигатель постоянного тока с независимым возбуждением Уравнение электрической цепи Потери в цепи ротора 2. Статическая характеристика двигателя Реактивные потери равны нулю: или: 21

МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЕЙ Электродвигатель постоянного тока с независимым возбуждением Уравнение электрической цепи 3. Динамическая характеристика двигателя 22

МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЕЙ Электродвигатель постоянного тока с независимым возбуждением 3. Динамическая характеристика двигателя L / R = t – электромагнитная постоянная времени k. M Ф / R = r – коэффициент пропорциональности – крутизна характеристики двигателя Линейная статическая характеристика двигателя: Линейная динамическая характеристика двигателя: 23

МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЕЙ Электродвигатель постоянного тока с независимым возбуждением Линейная статическая характеристика двигателя Рабочие характеристики Регулировочные характеристики Q u 3 Q = Q 1 = 0 u 2 Q 2 u = u 1 Q 3 u Регулировочная характеристика, соответствующая Q = 0 , называется характеристикой холостого хода. Характеристика холостого хода совпадает с идеальной кинематической характеристикой 24

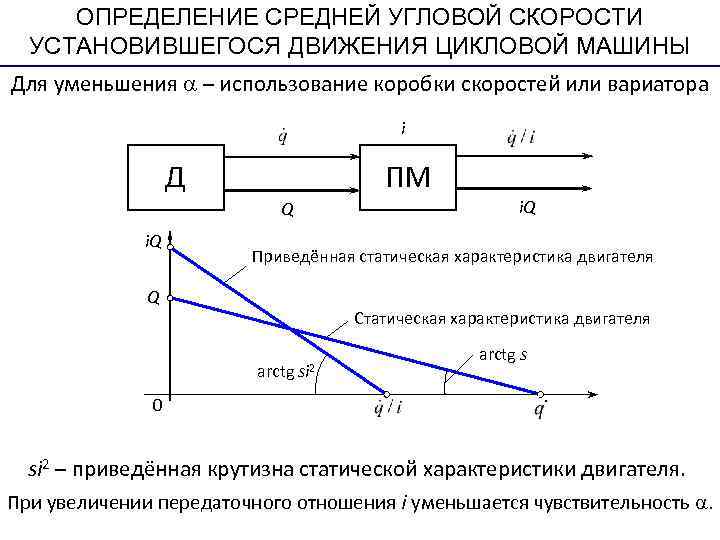
ОПРЕДЕЛЕНИЕ СРЕДНЕЙ УГЛОВОЙ СКОРОСТИ УСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ЦИКЛОВОЙ МАШИНЫ Для уменьшения – использование коробки скоростей или вариатора i Д ПМ Q i. Q Приведённая статическая характеристика двигателя Q Статическая характеристика двигателя arctg si 2 0 si 2 – приведённая крутизна статической характеристики двигателя. При увеличении передаточного отношения i уменьшается чувствительность .

УРАВНЕНИЯ ДВИЖЕНИЯ МАШИНЫ. РЕЖИМЫ ДВИЖЕНИЯ Уравнение движения: и идеальная кинематическая характеристика двигателя: Пусть характеристика двигателя – жёсткая. Движущий момент Q: Это – задача силового расчёта. Пусть характеристика двигателя – мягкая. Уравнение движения: 26

УРАВНЕНИЯ ДВИЖЕНИЯ МАШИНЫ. РЕЖИМЫ ДВИЖЕНИЯ 1. Установившееся движение u = u 0 = const 0 t Отклонение скорости вращения ротора от программной называется динамической ошибкой по скорости: 27

УРАВНЕНИЯ ДВИЖЕНИЯ МАШИНЫ. РЕЖИМЫ ДВИЖЕНИЯ 2. Переходные процессы а). Разбег t=0 t = tp 0 tр t u = u 0 = const – неуправляемый разбег 0 < u(t) < u 0 – управляемый разбег 28

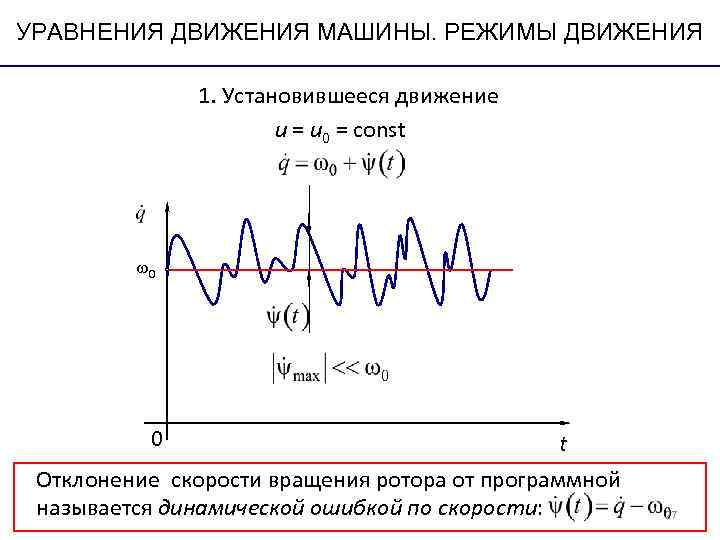
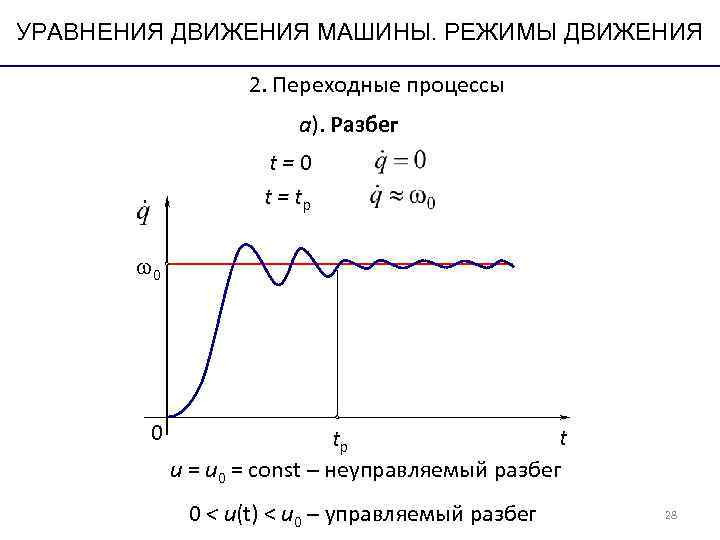
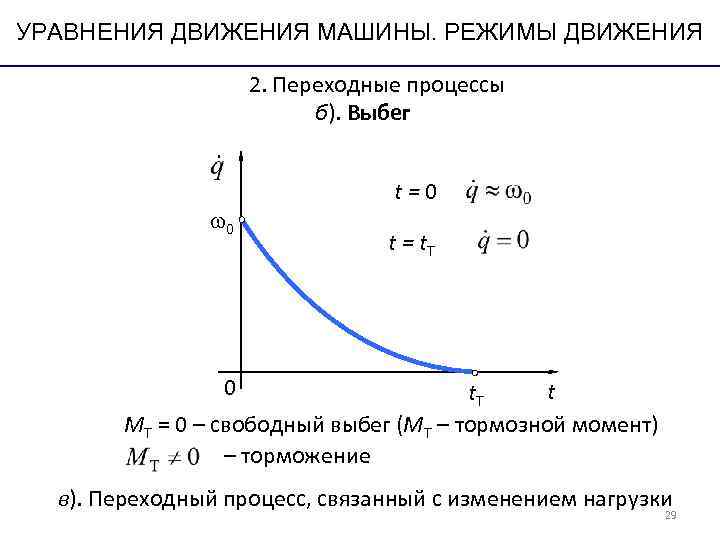
УРАВНЕНИЯ ДВИЖЕНИЯ МАШИНЫ. РЕЖИМЫ ДВИЖЕНИЯ 2. Переходные процессы б). Выбег t=0 t = t. Т 0 t. Т t МТ = 0 – свободный выбег (МТ – тормозной момент) – торможение в). Переходный процесс, связанный с изменением нагрузки 29