 Сила трения Занятие № 4
Сила трения Занятие № 4
 Очень часто при решении статических задач бывает необходимо учесть силу трения. Для описания силы трения пользуются законами Кулона: 1. Вектор силы трения лежит в общей касательной плоскости к поверхностям трущихся тел, тормозя движение одного тела по поверхности другого, и имеет величину, пропорциональную нормальной реакции N, действующей между телами: Т = k. N Коэффициент пропорциональности k называется коэффициентом трения. 2. Коэффициент трения не зависит от размеров соприкасающихся тел. 3. Коэффициент трения существенно зависит от материала трущихся тел и состояния поверхностей соприкосновения.
Очень часто при решении статических задач бывает необходимо учесть силу трения. Для описания силы трения пользуются законами Кулона: 1. Вектор силы трения лежит в общей касательной плоскости к поверхностям трущихся тел, тормозя движение одного тела по поверхности другого, и имеет величину, пропорциональную нормальной реакции N, действующей между телами: Т = k. N Коэффициент пропорциональности k называется коэффициентом трения. 2. Коэффициент трения не зависит от размеров соприкасающихся тел. 3. Коэффициент трения существенно зависит от материала трущихся тел и состояния поверхностей соприкосновения.
 При отсутствии относительного движения тел величина k не определена, и с ростом сдвигающей силы k тоже будет возрастать до некоторой предельной величины, называемой коэффициентом статического трения (трения покоя). При дальнейшем увеличении сдвигающей силы тела сдвигаются друг относительно друга и коэффициент трения падает до его значения при движении – коэффициента динамического трения. В теоретической механике считается, что он не зависит от скорости относительного движения.
При отсутствии относительного движения тел величина k не определена, и с ростом сдвигающей силы k тоже будет возрастать до некоторой предельной величины, называемой коэффициентом статического трения (трения покоя). При дальнейшем увеличении сдвигающей силы тела сдвигаются друг относительно друга и коэффициент трения падает до его значения при движении – коэффициента динамического трения. В теоретической механике считается, что он не зависит от скорости относительного движения.
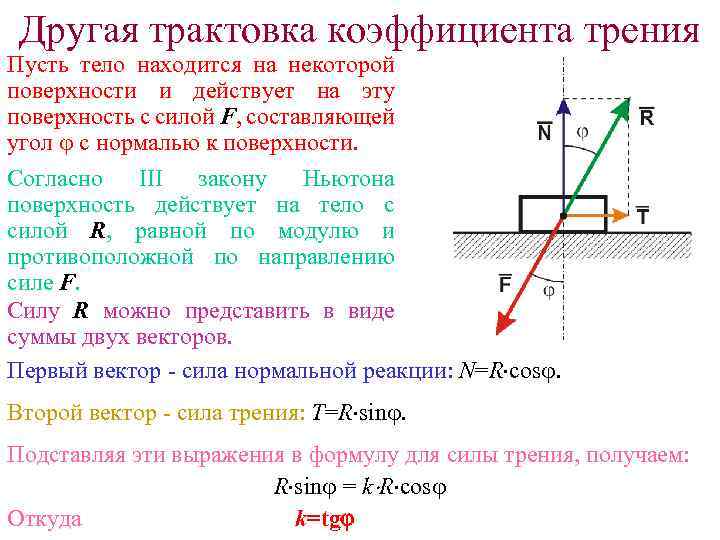 Другая трактовка коэффициента трения Пусть тело находится на некоторой поверхности и действует на эту поверхность с силой F, составляющей угол с нормалью к поверхности. Согласно III закону Ньютона поверхность действует на тело с силой R, равной по модулю и противоположной по направлению силе F. Силу R можно представить в виде суммы двух векторов. Первый вектор - сила нормальной реакции: N=R cos. Второй вектор - сила трения: T=R sin. Подставляя эти выражения в формулу для силы трения, получаем: R sin = k R cos Откуда k=tg
Другая трактовка коэффициента трения Пусть тело находится на некоторой поверхности и действует на эту поверхность с силой F, составляющей угол с нормалью к поверхности. Согласно III закону Ньютона поверхность действует на тело с силой R, равной по модулю и противоположной по направлению силе F. Силу R можно представить в виде суммы двух векторов. Первый вектор - сила нормальной реакции: N=R cos. Второй вектор - сила трения: T=R sin. Подставляя эти выражения в формулу для силы трения, получаем: R sin = k R cos Откуда k=tg
 • Предельное значение угла называется углом трения. Тело остается в покое, когда угол между нормалью к поверхности и направлением действующей силы не превосходит угла . Если этот угол больше – тело начинает скользить по поверхности. • Для решения задач, в которые входят силы трения, недостаточно только уравнений статики: их надо дополнять выражениями для силы трения. Поэтому такие задачи являются статически неопределимыми.
• Предельное значение угла называется углом трения. Тело остается в покое, когда угол между нормалью к поверхности и направлением действующей силы не превосходит угла . Если этот угол больше – тело начинает скользить по поверхности. • Для решения задач, в которые входят силы трения, недостаточно только уравнений статики: их надо дополнять выражениями для силы трения. Поэтому такие задачи являются статически неопределимыми.
 Примеры решения задач
Примеры решения задач
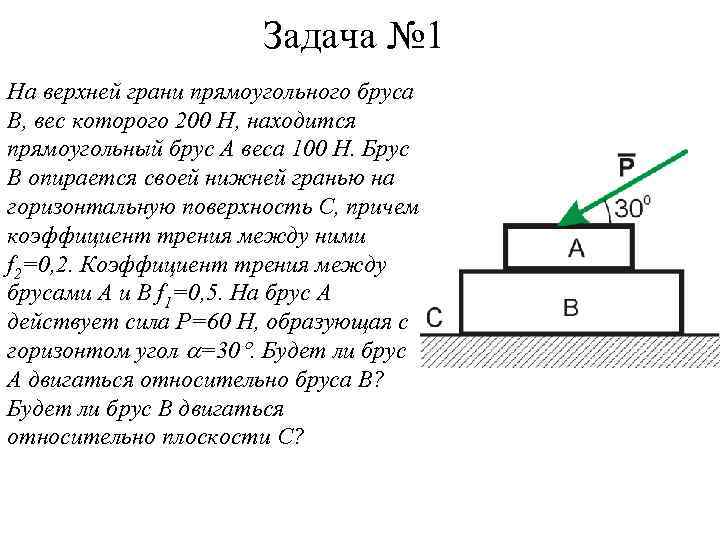 Задача № 1 На верхней грани прямоугольного бруса В, вес которого 200 Н, находится прямоугольный брус А веса 100 Н. Брус В опирается своей нижней гранью на горизонтальную поверхность С, причем коэффициент трения между ними f 2=0, 2. Коэффициент трения между брусами А и В f 1=0, 5. На брус А действует сила Р=60 Н, образующая с горизонтом угол =30. Будет ли брус А двигаться относительно бруса В? Будет ли брус В двигаться относительно плоскости С?
Задача № 1 На верхней грани прямоугольного бруса В, вес которого 200 Н, находится прямоугольный брус А веса 100 Н. Брус В опирается своей нижней гранью на горизонтальную поверхность С, причем коэффициент трения между ними f 2=0, 2. Коэффициент трения между брусами А и В f 1=0, 5. На брус А действует сила Р=60 Н, образующая с горизонтом угол =30. Будет ли брус А двигаться относительно бруса В? Будет ли брус В двигаться относительно плоскости С?
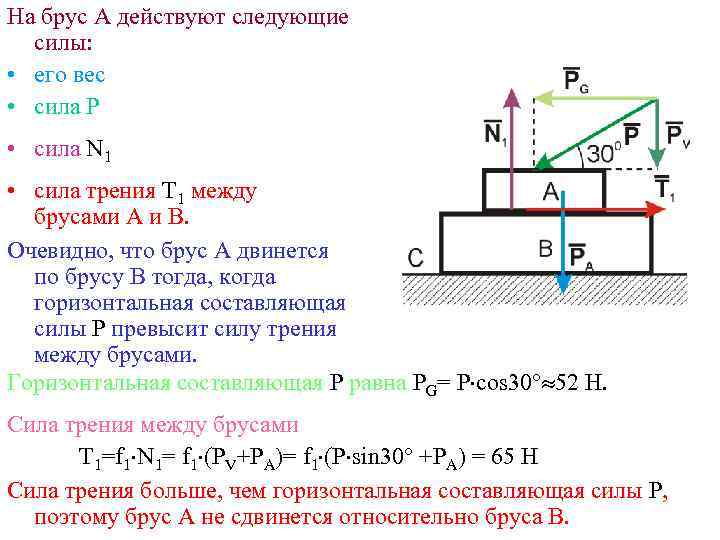 На брус А действуют следующие силы: • его вес • сила Р • сила N 1 • сила трения T 1 между брусами А и В. Очевидно, что брус А двинется по брусу В тогда, когда горизонтальная составляющая силы Р превысит силу трения между брусами. Горизонтальная составляющая P равна PG= P cos 30 52 Н. Сила трения между брусами T 1=f 1 N 1= f 1 (PV+PA)= f 1 (P sin 30 +PA) = 65 H Cила трения больше, чем горизонтальная составляющая силы Р, поэтому брус А не сдвинется относительно бруса В.
На брус А действуют следующие силы: • его вес • сила Р • сила N 1 • сила трения T 1 между брусами А и В. Очевидно, что брус А двинется по брусу В тогда, когда горизонтальная составляющая силы Р превысит силу трения между брусами. Горизонтальная составляющая P равна PG= P cos 30 52 Н. Сила трения между брусами T 1=f 1 N 1= f 1 (PV+PA)= f 1 (P sin 30 +PA) = 65 H Cила трения больше, чем горизонтальная составляющая силы Р, поэтому брус А не сдвинется относительно бруса В.
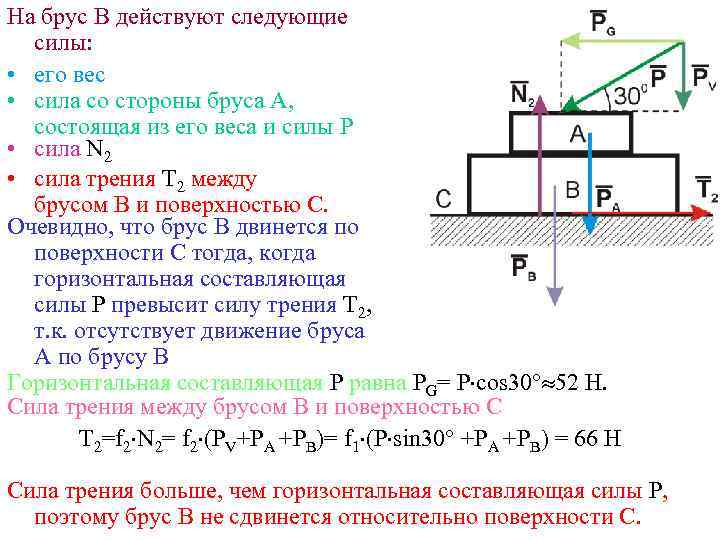 На брус B действуют следующие силы: • его вес • сила со стороны бруса А, состоящая из его веса и силы Р • сила N 2 • сила трения T 2 между брусом В и поверхностью С. Очевидно, что брус В двинется по поверхности С тогда, когда горизонтальная составляющая силы Р превысит силу трения Т 2, т. к. отсутствует движение бруса А по брусу В Горизонтальная составляющая P равна PG= P cos 30 52 Н. Сила трения между брусом В и поверхностью С T 2=f 2 N 2= f 2 (PV+PA +PВ)= f 1 (P sin 30 +PA +PВ) = 66 H Cила трения больше, чем горизонтальная составляющая силы Р, поэтому брус В не сдвинется относительно поверхности С.
На брус B действуют следующие силы: • его вес • сила со стороны бруса А, состоящая из его веса и силы Р • сила N 2 • сила трения T 2 между брусом В и поверхностью С. Очевидно, что брус В двинется по поверхности С тогда, когда горизонтальная составляющая силы Р превысит силу трения Т 2, т. к. отсутствует движение бруса А по брусу В Горизонтальная составляющая P равна PG= P cos 30 52 Н. Сила трения между брусом В и поверхностью С T 2=f 2 N 2= f 2 (PV+PA +PВ)= f 1 (P sin 30 +PA +PВ) = 66 H Cила трения больше, чем горизонтальная составляющая силы Р, поэтому брус В не сдвинется относительно поверхности С.
 Задача № 2 Листы бумаги, сложенные, как показано на рисунке, склеиваются свободными концами через лист, так что получаются две самостоятельные кипы А и В. Вес каждого листа Q=0, 06 Н, число всех листов 200, коэффициент трения бумаги о бумагу, а также о стол, на котором бумага лежит, равен 0, 2. Предполагая, что одна из кип удерживается неподвижно, определить наименьшее горизонтальное усилие Р, необходимое для того, чтобы вытащить вторую кипу.
Задача № 2 Листы бумаги, сложенные, как показано на рисунке, склеиваются свободными концами через лист, так что получаются две самостоятельные кипы А и В. Вес каждого листа Q=0, 06 Н, число всех листов 200, коэффициент трения бумаги о бумагу, а также о стол, на котором бумага лежит, равен 0, 2. Предполагая, что одна из кип удерживается неподвижно, определить наименьшее горизонтальное усилие Р, необходимое для того, чтобы вытащить вторую кипу.
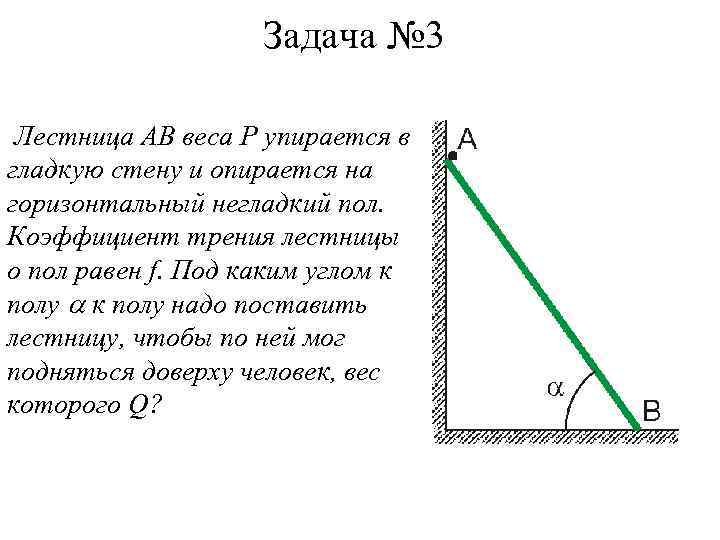 Задача № 3 Лестница АВ веса Р упирается в гладкую стену и опирается на горизонтальный негладкий пол. Коэффициент трения лестницы о пол равен f. Под каким углом к полу надо поставить лестницу, чтобы по ней мог подняться доверху человек, вес которого Q?
Задача № 3 Лестница АВ веса Р упирается в гладкую стену и опирается на горизонтальный негладкий пол. Коэффициент трения лестницы о пол равен f. Под каким углом к полу надо поставить лестницу, чтобы по ней мог подняться доверху человек, вес которого Q?
 Согласно условия задачи, на лестницу АВ действуют следующие силы: • вес лестницы Р, • вес человека наверху Q, • нормальная реакция стены в точке А NA, • нормальная реакция пола в точке В NВ • сила трения между полом и лестницей F Согласно общему порядку решения задач статики с произвольной системой сил, необходимо ввести систему координат и составить уравнения равновесия. Уравнения равновесия выглядят так (l – длина лестницы): Ox: NA - F = 0; Oy: -Q - P + NB = 0; mom. B: Q l cos - NA l sin + P (l/2) cos = 0
Согласно условия задачи, на лестницу АВ действуют следующие силы: • вес лестницы Р, • вес человека наверху Q, • нормальная реакция стены в точке А NA, • нормальная реакция пола в точке В NВ • сила трения между полом и лестницей F Согласно общему порядку решения задач статики с произвольной системой сил, необходимо ввести систему координат и составить уравнения равновесия. Уравнения равновесия выглядят так (l – длина лестницы): Ox: NA - F = 0; Oy: -Q - P + NB = 0; mom. B: Q l cos - NA l sin + P (l/2) cos = 0
 Так как уравнений статики – три, а неизвестных – четыре (две нормальные реакции, сила трения и угол наклона лестницы), то для того, чтобы решить задачу, необходимо дополнить систему уравнений статики соотношением для силы трения: F=f NB. После подстановки и элементарных преобразований получается следующая система для трех неизвестных: Из первых двух уравнений находятся NA и NB; после их подстановки в последнее уравнение получается следующая формула для угла наклона : Если угол наклона будет меньше угла , то момент сил тяжести. Q и P окажется больше момента силы NA относительно точки В, и лестница соскользнет вниз. Если же угол будет больше – момент силы тяжести будет меньше, и лестница останется в покое.
Так как уравнений статики – три, а неизвестных – четыре (две нормальные реакции, сила трения и угол наклона лестницы), то для того, чтобы решить задачу, необходимо дополнить систему уравнений статики соотношением для силы трения: F=f NB. После подстановки и элементарных преобразований получается следующая система для трех неизвестных: Из первых двух уравнений находятся NA и NB; после их подстановки в последнее уравнение получается следующая формула для угла наклона : Если угол наклона будет меньше угла , то момент сил тяжести. Q и P окажется больше момента силы NA относительно точки В, и лестница соскользнет вниз. Если же угол будет больше – момент силы тяжести будет меньше, и лестница останется в покое.
 Задача № 4 Однородный стержень своими концами А и В может скользить своими концами по негладкой окружности радиуса а. Расстояние ОС стержня от центра О окружности, расположенной в вертикальной плоскости, равно b. Коэффициент трения между стержнем и окружностью равен f. Определить для положений равновесия стержня угол , составляемый прямой ОС с вертикальным диаметром окружности
Задача № 4 Однородный стержень своими концами А и В может скользить своими концами по негладкой окружности радиуса а. Расстояние ОС стержня от центра О окружности, расположенной в вертикальной плоскости, равно b. Коэффициент трения между стержнем и окружностью равен f. Определить для положений равновесия стержня угол , составляемый прямой ОС с вертикальным диаметром окружности
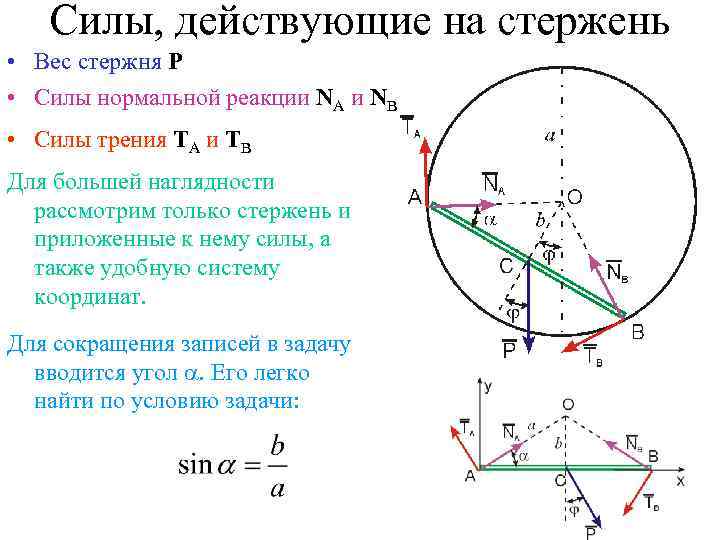 Силы, действующие на стержень • Вес стержня P • Cилы нормальной реакции NA и NB • Cилы трения TA и TB Для большей наглядности рассмотрим только стержень и приложенные к нему силы, а также удобную систему координат. Для сокращения записей в задачу вводится угол . Его легко найти по условию задачи:
Силы, действующие на стержень • Вес стержня P • Cилы нормальной реакции NA и NB • Cилы трения TA и TB Для большей наглядности рассмотрим только стержень и приложенные к нему силы, а также удобную систему координат. Для сокращения записей в задачу вводится угол . Его легко найти по условию задачи:
 Уравнения статики составляются обычным образом. Для того, чтобы уравнение моментов оказалось проще, целесообразно моменты вычислять относительно центра окружности О. К этим уравнениям нужно добавить соотношения для сил трения: ТА = f NA, ТB = f NB
Уравнения статики составляются обычным образом. Для того, чтобы уравнение моментов оказалось проще, целесообразно моменты вычислять относительно центра окружности О. К этим уравнениям нужно добавить соотношения для сил трения: ТА = f NA, ТB = f NB
 После подстановки этих выражений в систему и элементарных преобразований, система уравнений статики станет такой: Из первых двух уравнений легко определить сумму (NA+NB): Если подставить это выражение в уравнение для моментов и сократить Р, то получится уравнение для определения угла : После деления этого уравнения на sin и замены sin по формуле получается окончательное выражение для искомого угла:
После подстановки этих выражений в систему и элементарных преобразований, система уравнений статики станет такой: Из первых двух уравнений легко определить сумму (NA+NB): Если подставить это выражение в уравнение для моментов и сократить Р, то получится уравнение для определения угла : После деления этого уравнения на sin и замены sin по формуле получается окончательное выражение для искомого угла:


