Signal Processing First Lecture 10 FIR Filtering Intro

Signal Processing First Lecture 10 FIR Filtering Intro 2018 -03 -16 cwpark 1@kangnung. ac. kr (Chapter 05) 1

READING ASSIGNMENTS § This Lecture: § Chapter 5, Sects. 5 -1, 5 -2 and 5 -3 (partial) § Other Reading: § Recitation: Ch. 5, Sects 5 -4, 5 -6, 5 -7 and 5 -8 § CONVOLUTION § Next Lecture: Ch 5, Sects. 5 -3, 5 -5 and 5 -6 2018 -03 -16 cwpark 1@kangnung. ac. kr 2

Chapter 05 FIR 필터 Filter : 신호가 가지는 어떠한 특성을 변경하거나 신호의 어떤 구성요소를 없애는 하나의 시스템 FIR(유한 임펄스 응답 : finite impulse response) : 입력 신호열에서 한정된 개수의 샘플에 일정한 계수를 곱하고 이를 더한 합 - 이산시간 시스템의 기본개념, 수학적 표현과 조작 2018 -03 -16 cwpark 1@kangnung. ac. kr 3

5. 1 이산시간 시스템 샘플링의 경우; 입력(연속시간 신호), 출력(이산시간 신호) 복원과정; 이산시간 시스템 ; 입력, 출력 모두 이산신호 시스템의 작용; 입력 신호열이 출력 신호열로 변화 y[n] = T{x[n]} 여기서, T는 연산자 ex) 제곱 시스템, 연속된 3개의 입력 값과 관련 2018 -03 -16 cwpark 1@kangnung. ac. kr 4

5. 2 이동 평균 필터 ; 두 개 이상의 연속된 입력 값의 평균을 계속적으로 계산하는 것 FIR 필터의 한 종류 그림 5 -2(p. 109) 3점 (삼각형 형태의 입력 신호열에)이동 평균 적용 유한길이 신호의 예 0이 아닌 구간(지원)은 유한기간 0<=n<=4 이다. {x[0], x[1], x[2]}={2, 4, 6}에 대한 3점 이동 평균 답은 {4, 6, 4}을 평균하여 14/3 2018 -03 -16 cwpark 1@kangnung. ac. kr 5

여러 가지 표현 가능한 방법 중에 한 경우, 출력을 계산하는 수식 y[0] = (1/3)(x[0]+x[1]+x[2]), y[1] = (1/3)(x[1]+x[2]+x[3]) 일반화, 차분방정식 ; 모든 y[n]에 대하여 출력을 계산 y[n] = (1/3)(x[n]+x[n+1]+x[n+2]) n n<-2 -2 -1 0 1 2 3 4 5 n>5 x[n] 0 0 0 2 4 6 4 2 0 0 y[n] 0 2/3 2 4 14/3 4 2 2/3 0 0 이동평균 FIR 필터의 특성, 세 샘플의 슬라이딩 윈도우 (n: 현재, n+1, n+2: 미래) 2018 -03 -16 cwpark 1@kangnung. ac. kr 6

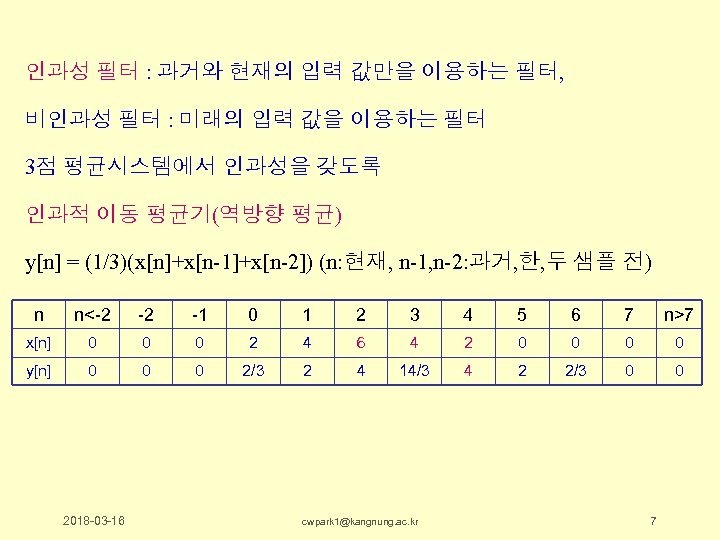인과성 필터 : 과거와 현재의 입력 값만을 이용하는 필터, 비인과성 필터 : 미래의 입력 값을 이용하는 필터 3점 평균시스템에서 인과성을 갖도록 인과적 이동 평균기(역방향 평균) y[n] = (1/3)(x[n]+x[n-1]+x[n-2]) (n: 현재, n-1, n-2: 과거, 한, 두 샘플 전) n n<-2 -2 -1 0 1 2 3 4 5 6 7 n>7 x[n] 0 0 0 2 4 6 4 2 0 0 y[n] 0 0 0 2/3 2 4 14/3 4 2 2/3 0 0 2018 -03 -16 cwpark 1@kangnung. ac. kr 7

5. 3 일반적인 FIR 필터 ; 일반 차분방정식, M=2(차수), k=0, 1, 2 bk=1/3(계수의 개수, 필터 길이) ; 계수 bk 들이 서로 같지 않으면, M=1개의 샘플에 가중치가 곱해진 이동 평균기 인과성을 가짐, 입력이 시작되기 전에는 출력이 나오지 않음 출력의 길이가 입력의 길이보다 M개가 크다. 2018 -03 -16 cwpark 1@kangnung. ac. kr 8

예제 5. 1) FIR 필터 계수 {bk}={3, -1, 2, 1}, M(차수)=3, 필터의 길이(계수 개수)=4 -> 4점 차분방정식 y[n] = 3 x[n]-x[n-1]+2 x[n-2]+x[n-3] ; 길이는 차수보다 1 크다 2018 -03 -16 cwpark 1@kangnung. ac. kr 9

예제 5. 2) FIR 필터 계수 {bk}={3, -1, 2, 1}, 필터 길이=4, y[n]? 입력 : 그림 5 -2, 빠진 부분을 채워 넣어라. -> y[2] = 6*3+4*(-1)+2*2+1*0 = 18 -4+4+0 = 18 y[3] = 4*3+6*(-1)+4*2+2*1 = 12 -6+8+2 = 16 y[4] = 2*3+4*(-1)+6*2+4*1 = 6 -4+12+4 = 18 y[5] = 0*3+2*(-1)+4*2+6*1 = 0 -2+8+6 = 12 y[6] = 0*3+0*(-1)+2*2+4*1 = 0+0+4+4 = 8 n n<0 0 1 2 3 4 5 6 7 8 n>8 x[n] 0 2 4 6 4 2 0 0 0 y[n] 0 6 10 18 ? ? ? 8 2 0 0 2018 -03 -16 cwpark 1@kangnung. ac. kr 10

5. 3. 1 FIR 필터의 설명묭 원 신호 + 원치 않는 신호(잡음) 인과성 3점 이동평균 ; 입력 x[n], M=2, 모든 계수 1/3, 필터의 출력, 그림 5 -6의 (b) (a) 입력신호 x[n]은, n=0 이전에는 0, n<0에서 출력 0 (b) 출력은 n=0에서 부터 0 이 아닌 값을 가짐, 길이 M=2인 음영구간은, 입력을 “시작하는 구간” 입력이 모두 0이 아닌 구간, 2 <= n <= 40 (c) n=40 이후, 길이 M=2인 또 다른 음영구간은, 입력에서 “빠져 나가는 구간” (d) 정현파성분이 줄어 들었음, 인과성 필터를 이용함으로써 M/2=1 만큼 이동했음 -> 잡음이 어느 정도 줄어듦, 2018 -03 -16 cwpark 1@kangnung. ac. kr 11

인과성 7점 이동 평균 ; 입력 x[n], M=6, 모든 계수 1/7, 필터의 출력, 그림 5 -6의 (c) (a) 출력의 시작과 끝의 음영구간의 길이는 모두 M=6 (b) 정현파 성분의 크기는 입력신호와 비교했을 경우, 상당히 줄어듦, 지수 성분도 입력의 지수 성분과 유사함 결론; 1. FIR 필터를 이용하여 신호를 유용하도록 변형할 수 있음 2. 평균구간 길이는 출력에 크게 영향을 미침 3. 이동평균을 하면 M/2만큼 지연 2018 -03 -16 cwpark 1@kangnung. ac. kr 12

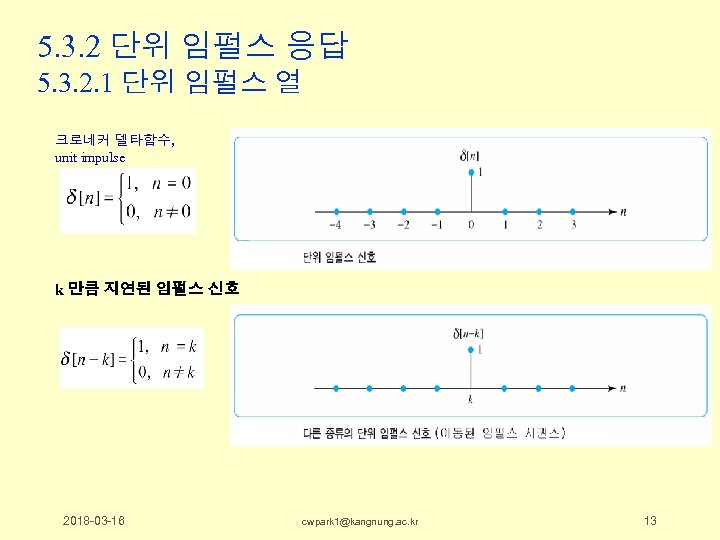5. 3. 2 단위 임펄스 응답 5. 3. 2. 1 단위 임펄스 열 크로네커 델타함수, unit impulse k 만큼 지연된 임펄스 신호 2018 -03 -16 cwpark 1@kangnung. ac. kr 13

이동된 임펄스는 신호와 시스템을 표현하는데 유용. Let, x[n] = 2δ[n]+4δ[n-1]+6δ[n-2]+4δ[n-3]+2δ[n-4] 각각의 신호열과 그 합 n … -2 -1 0 1 2 3 4 5 6 … 2δ[n] 0 0 0 2 0 0 0 0 4δ[n-1] 0 0 4 0 0 0 6δ[n-2] 0 0 0 6 0 0 0 4δ[n-3] 0 0 0 4 0 0 2δ[n-4] 0 0 0 0 2 0 0 0 x[n] 0 0 0 2 4 6 4 2 0 0 0 어떤 신호열이든 이 방법으로 표현이 가능함 ; 샘플들은, 가중치를 곱하고 이동된 임펄스들의 합 2018 -03 -16 cwpark 1@kangnung. ac. kr 14

5. 3. 2. 2 (단위) 임펄스 응답 ; x[n] =δ[n]이 입력되었을 때의 출력 y[n] = h[n] n=k 일 때만 0이 아니기 때문에 합은, n의 각각의 값에서 하나의 항만 고려하면 된다. 임펄스 응답을 표로 표시하면, n n<0 0 1 2 3 … M M+1 n>M x[n]=δ[n] 0 1 0 0 0 0 y[n]=h[n] 0 b 1 b 2 b 3 … b. M 0 0 ; FIR 필터의 임펄스 응답 h[n]은 차분 방정식의 계수들의 신호 열. n<0 와 n>M 일때 h[n] =0, h[n]의 길이 유한, 유한 임펄스 응답 (FIR) 시스템. 2018 -03 -16 cwpark 1@kangnung. ac. kr 15

5. 3. 2. 3 단위 지연 시스템 n 0 만큼 지연된 시스템 ; y[n] = x[n-n 0] n 0=1 일때, unit delay -> 가장 간단한 FIR 필터 예) y[4]는 x[3]값을 가지고, y[6]은 x[5]값을 가지는 형식으로 진행. . 예) “ 2만큼 지연” 시스템의 필터 계수 {bk} = {0, 0, 1}, M=2 차분방정식, y[n] = b 0 x[n] + b 1 x[n-1] + b 2 x[n-2] = 0 x[n] + 0 x[n-1] + 1 x[n-2] = x[n-2] 2만큼 지연하는 시스템과 임펄스 응답 2018 -03 -16 cwpark 1@kangnung. ac. kr 16

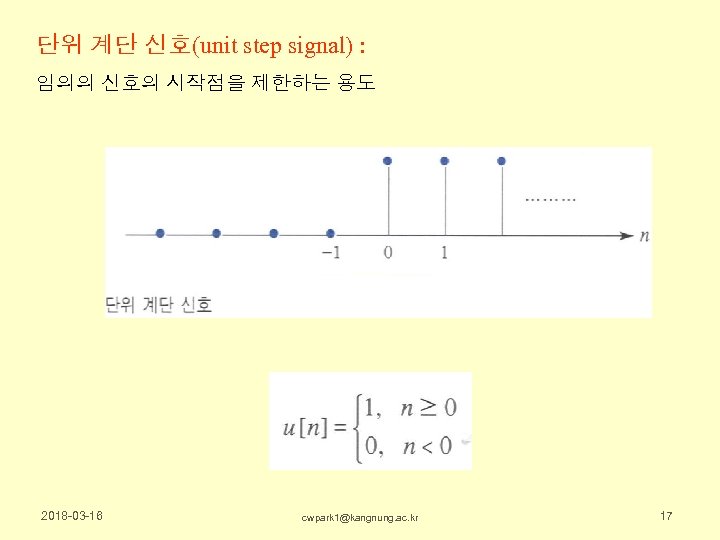단위 계단 신호(unit step signal) : 임의의 신호의 시작점을 제한하는 용도 2018 -03 -16 cwpark 1@kangnung. ac. kr 17

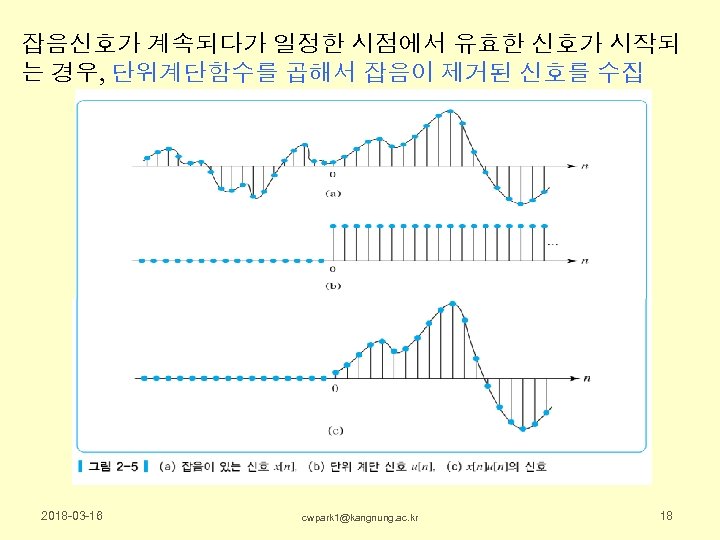잡음신호가 계속되다가 일정한 시점에서 유효한 신호가 시작되 는 경우, 단위계단함수를 곱해서 잡음이 제거된 신호를 수집 2018 -03 -16 cwpark 1@kangnung. ac. kr 18

5. 3. 3 콘볼루션과 FIR 필터의 출력 ; 임펄스 응답 이용, 필터의 계수 = 임펄스 응답값 bk를 h[k]로 바꾸면, Convolution sum : FIR 필터의 입력과 출력간의 관계 출력 ; 두신호 열 x[n], h[n]의 콘볼루션. 2018 -03 -16 cwpark 1@kangnung. ac. kr 19

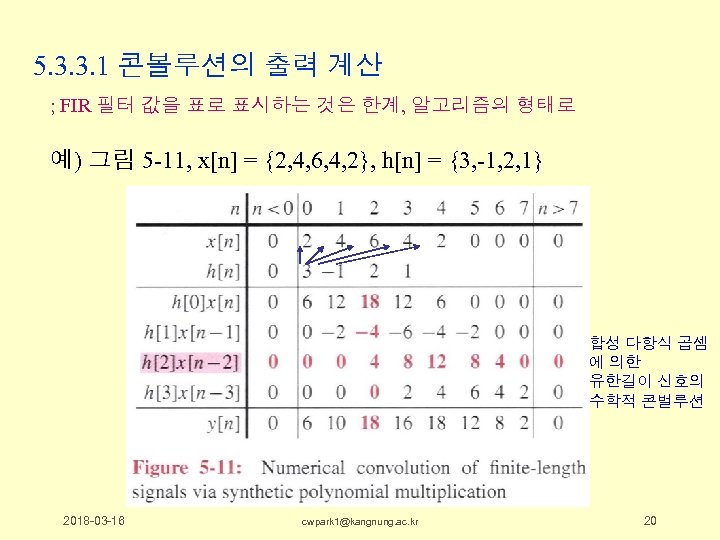5. 3. 3. 1 콘볼루션의 출력 계산 ; FIR 필터 값을 표로 표시하는 것은 한계, 알고리즘의 형태로 예) 그림 5 -11, x[n] = {2, 4, 6, 4, 2}, h[n] = {3, -1, 2, 1} 합성 다항식 곱셈 에 의한 유한길이 신호의 수학적 콘벌루션 2018 -03 -16 cwpark 1@kangnung. ac. kr 20

; 무한한 길이의 신호에도 적용할 수 있는 콘벌루션의 일반적인 형태 ; 합이 구간은 무한대, n < 0과 n > M 구간에서 h[n]=0 이면, 식 (5. 10)과 같다. 2018 -03 -16 cwpark 1@kangnung. ac. kr 21

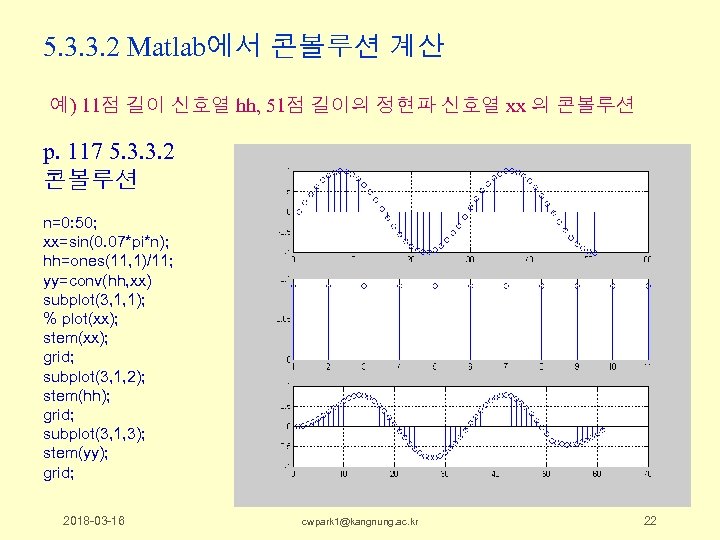5. 3. 3. 2 Matlab에서 콘볼루션 계산 예) 11점 길이 신호열 hh, 51점 길이의 정현파 신호열 xx 의 콘볼루션 p. 117 5. 3. 3. 2 콘볼루션 n=0: 50; xx=sin(0. 07*pi*n); hh=ones(11, 1)/11; yy=conv(hh, xx) subplot(3, 1, 1); % plot(xx); stem(xx); grid; subplot(3, 1, 2); stem(hh); grid; subplot(3, 1, 3); stem(yy); grid; 2018 -03 -16 cwpark 1@kangnung. ac. kr 22

예) 11점 이동 평균 시스템, 11개 필터계수는 모두 1/11로 동일. 2018 -03 -16 cwpark 1@kangnung. ac. kr 23

Ex 5 -6) Matlab을 이용, 다항식의 곱셈 ? p 1 = [5 0 3 2 1]; p 2 = [3 1 -1 -3 1]; conv(p 1, p 2) ans = 15 2018 -03 -16 5 4 -6 7 -10 -4 -1 cwpark 1@kangnung. ac. kr 1 24

5. 4 FIR 필터의 구현 FIR 필터의 일반식 시스템을 구현하는 방법 (1) 필터계수와 지연된 입력신호와 곱하는 방법 (2) 가중치를 곱한 신호열을 더하는 방법 (3) 입력신호열을 지연시키는 방법 (4) 블럭도를 표현하면 매우 유용 2018 -03 -16 cwpark 1@kangnung. ac. kr 25

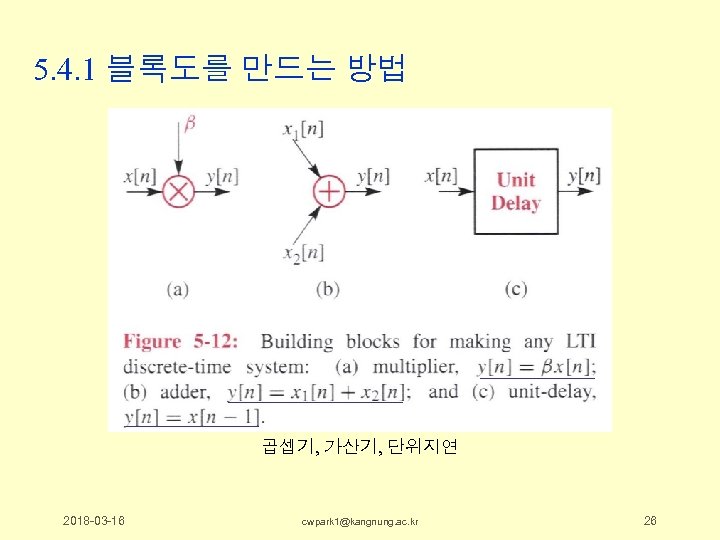5. 4. 1 블록도를 만드는 방법 곱셉기, 가산기, 단위지연 2018 -03 -16 cwpark 1@kangnung. ac. kr 26

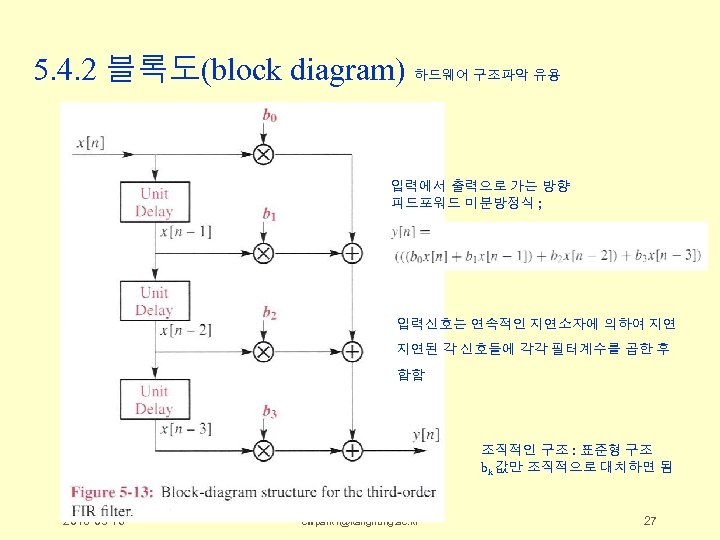5. 4. 2 블록도(block diagram) 하드웨어 구조파악 유용 입력에서 출력으로 가는 방향 피드포워드 미분방정식 ; 입력신호는 연속적인 지연소자에 의하여 지연 지연된 각 신호들에 각각 필터계수를 곱한 후 합함 조직적인 구조 : 표준형 구조 bk 값만 조직적으로 대치하면 됨 2018 -03 -16 cwpark 1@kangnung. ac. kr 27

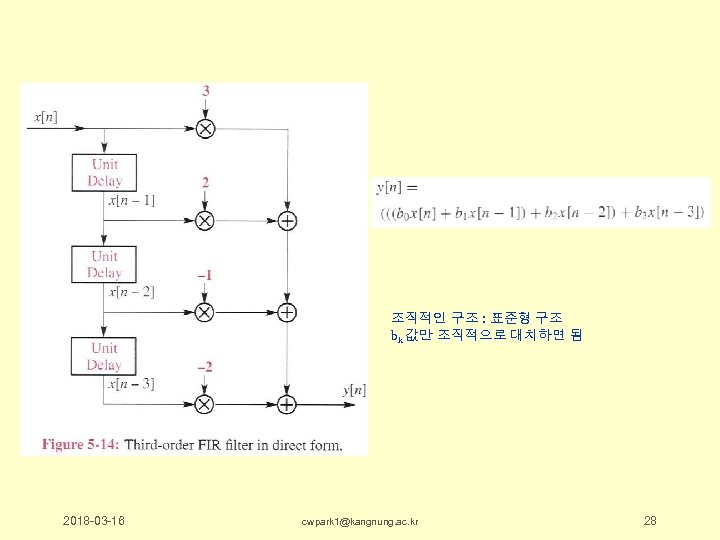조직적인 구조 : 표준형 구조 bk 값만 조직적으로 대치하면 됨 2018 -03 -16 cwpark 1@kangnung. ac. kr 28

5. 4. 2. 1 기타 블록도 입력과 출력의 관계만 같으면 된다는 개념에서 다른 형태의 블록도를 이용할 수도 있음 임의의 블록도에 대하여 차분방정식을 끌어내기 위한 4단계 (a) 각 단위지연 블록의 입력에 대해 서로 다른 신호의 이름을 붙여라 (b) 단위지연의 출력은 입력신호 이름을 이용하여 표시할 수 있다. (c) 블록도에서 합쳐지는 노드에서는 신호식을 써보아라 신호의 이름은, 1, 2 단계에서 정의된 것을 이용하라. (d) 그러면 x[n], y[n]을 비롯하여 내부에서 정의된 여러 가지 신호들로 이루어진 여러 개의 방정식이 있게 된다. 여기서 내부에서 정의된 신호들의 이름을 다소거 하고 x[n], y[n]으로만 이루어진 하나의 차분방정식을 유도해 내어라 2018 -03 -16 cwpark 1@kangnung. ac. kr 29

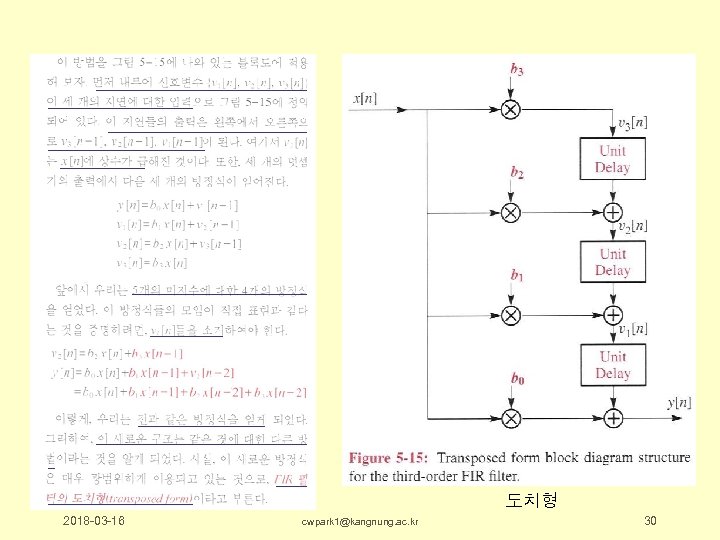도치형 2018 -03 -16 cwpark 1@kangnung. ac. kr 30

5. 4. 2. 2 내부 하드웨어 자세히 보기 다른 신호들간의 종속성을 파악, 내부에서 일어나는 매우 다른 특성 (a) 계산의 순서가 블록도에 의하여 결정됨, 평행 동시계산이나 파이프라인 연속 계산이 이용되어야 하는 고속 응용인 경우에는, 블록에서 신호들간의 종속성이 걸림돌이 됨. (b) VLSI 칩을 만들 때, 블록도에 따라서 구획이 나누어진다. 마찬가지로 특별한 DSP구조에 매핑되는 알고리즘은, 블록도를 해당 DSP 칩에 가장 최적화된 코드로 변환하는 컴파일러를 사용하여 다루어진다. (c) 필터를 고정소수점 연산으로 구현하면, 단어길이와 유한성 효과가 매우 크다. 이 경우에는, 반올림에 의한 오차와 넘침이 얼마나 일어나는가 하는 것은 계산의 순서와 매우 밀접하게 관련된다. 2018 -03 -16 cwpark 1@kangnung. ac. kr 31

LECTURE OBJECTIVES § INTRODUCE FILTERING IDEA § Weighted Average § Running Average § FINITE IMPULSE RESPONSE FILTERS § FIR Filters § Show to compute the output y[n] from the input signal, x[n] 2018 -03 -16 cwpark 1@kangnung. ac. kr 32

DIGITAL FILTERING x(t) A-to-D x[n] COMPUTER y[n] D-to-A y(t) § CONCENTRATE on the COMPUTER § PROCESSING ALGORITHMS § SOFTWARE (MATLAB) § HARDWARE: DSP chips, VLSI § DSP: DIGITAL SIGNAL PROCESSING 2018 -03 -16 cwpark 1@kangnung. ac. kr 33

The TMS 32010, 1983 First PC plug-in board from Atlanta Signal Processors Inc. 2018 -03 -16 cwpark 1@kangnung. ac. kr 34

Rockland Digital Filter, 1971 For the price of a small house, you could have one of these. 2018 -03 -16 cwpark 1@kangnung. ac. kr 35

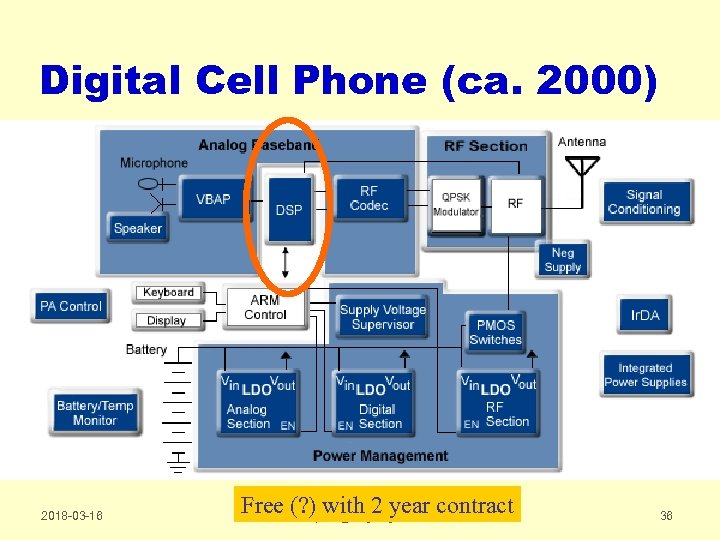Digital Cell Phone (ca. 2000) 2018 -03 -16 Free (? ) with 2 year contract cwpark 1@kangnung. ac. kr 36

DISCRETE-TIME SYSTEM x[n] COMPUTER y[n] § OPERATE on x[n] to get y[n] § WANT a GENERAL CLASS of SYSTEMS § ANALYZE the SYSTEM § TOOLS: TIME-DOMAIN & FREQUENCY-DOMAIN § SYNTHESIZE the SYSTEM 2018 -03 -16 cwpark 1@kangnung. ac. kr 37

D-T SYSTEM EXAMPLES x[n] SYSTEM y[n] § EXAMPLES: § POINTWISE OPERATORS § SQUARING: y[n] = (x[n])2 § RUNNING AVERAGE § RULE: “the output at time n is the average of three consecutive input values” 2018 -03 -16 cwpark 1@kangnung. ac. kr 38

DISCRETE-TIME SIGNAL § x[n] is a LIST of NUMBERS § INDEXED by “n” STEM PLOT 2018 -03 -16 cwpark 1@kangnung. ac. kr 39

3 -PT AVERAGE SYSTEM § ADD 3 CONSECUTIVE NUMBERS § Do this for each “n” Make a TABLE n=0 2018 -03 -16 n=1 cwpark 1@kangnung. ac. kr 40

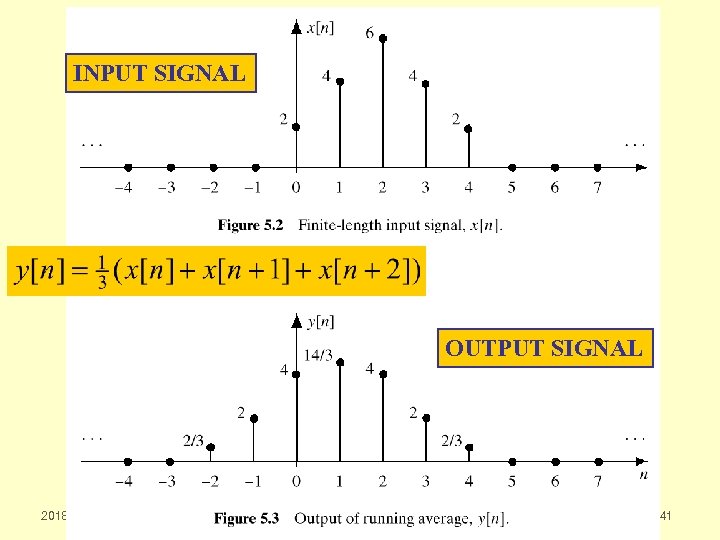INPUT SIGNAL OUTPUT SIGNAL 2018 -03 -16 cwpark 1@kangnung. ac. kr 41

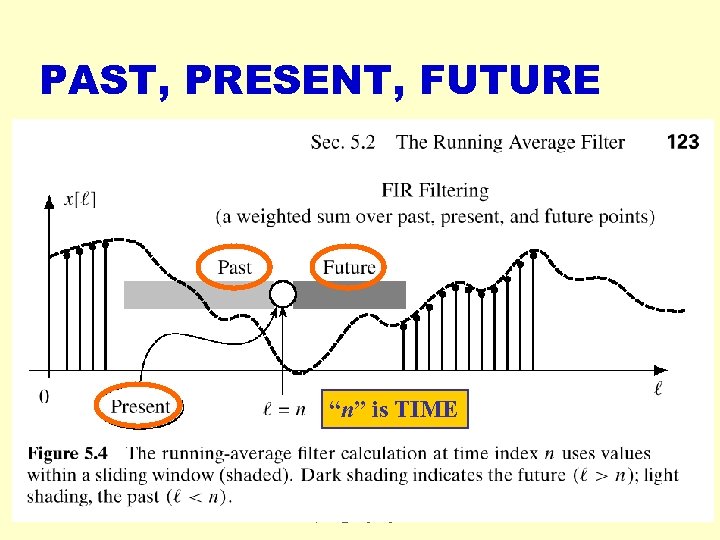PAST, PRESENT, FUTURE “n” is TIME 2018 -03 -16 cwpark 1@kangnung. ac. kr 42

ANOTHER 3 -pt AVERAGER § Uses “PAST” VALUES of x[n] § IMPORTANT IF “n” represents REAL TIME § WHEN x[n] & y[n] ARE STREAMS 2018 -03 -16 cwpark 1@kangnung. ac. kr 43

GENERAL FIR FILTER § FILTER COEFFICIENTS {bk} § DEFINE THE FILTER § For example, 2018 -03 -16 cwpark 1@kangnung. ac. kr 44

GENERAL FIR FILTER § FILTER COEFFICIENTS {bk} § FILTER ORDER is M § FILTER LENGTH is L = M+1 § NUMBER of FILTER COEFFS is L 2018 -03 -16 cwpark 1@kangnung. ac. kr 45

GENERAL FIR FILTER § SLIDE a WINDOW across x[n] 2018 -03 -16 x[n-M] x[n] cwpark 1@kangnung. ac. kr 46

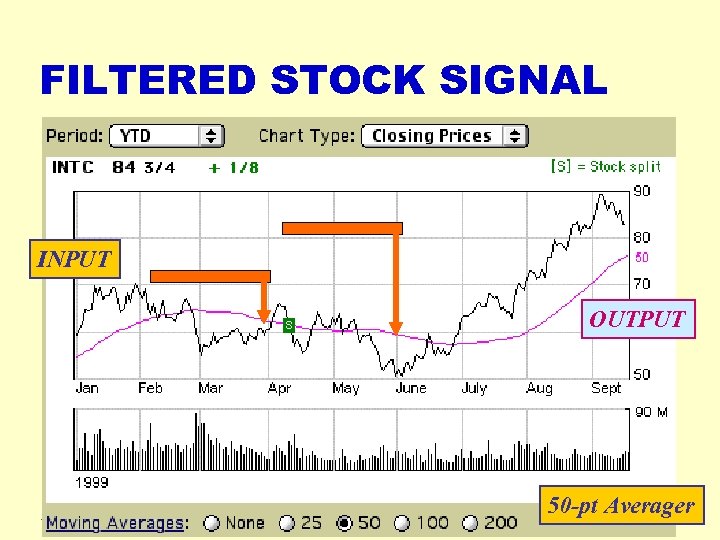FILTERED STOCK SIGNAL INPUT OUTPUT 2018 -03 -16 cwpark 1@kangnung. ac. kr 50 -pt Averager 47

UNIT IMPULSE SIGNAL d[n] FREQUENCY RESPONSE (LATER) UNIT-IMPULSE 1 n 2018 -03 -16 cwpark 1@kangnung. ac. kr 48

UNIT IMPULSE SIGNAL d[n] is NON-ZERO When its argument is equal to ZERO 2018 -03 -16 cwpark 1@kangnung. ac. kr 49

MATH FORMULA for x[n] § Use SHIFTED IMPULSES to write x[n] 2018 -03 -16 cwpark 1@kangnung. ac. kr 50

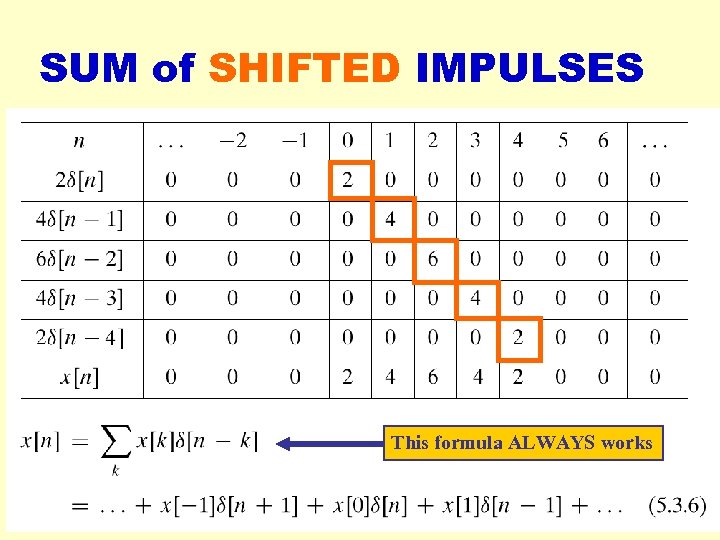SUM of SHIFTED IMPULSES This formula ALWAYS works 2018 -03 -16 cwpark 1@kangnung. ac. kr 51

4 -pt AVERAGER § CAUSAL SYSTEM: USE PAST VALUES § INPUT = UNIT IMPULSE SIGNAL = d[n] § OUTPUT is called “IMPULSE RESPONSE” 2018 -03 -16 cwpark 1@kangnung. ac. kr 52

4 -pt Avg Impulse Response d[n] “READS OUT” the FILTER COEFFICIENTS “h” in h[n] denotes Impulse Response n=0 n=– 1 n=0 NON-ZERO When window overlaps d[n] 1 n=1 n n=4 n=5 2018 -03 -16 cwpark 1@kangnung. ac. kr 53

FIR IMPULSE RESPONSE § Convolution = Filter Definition § Filter Coeffs = Impulse Response CONVOLUTION 2018 -03 -16 cwpark 1@kangnung. ac. kr 54

FILTERING EXAMPLE § 7 -point AVERAGER § Removes cosine § By making its amplitude (A) smaller § 3 -point AVERAGER § Changes A slightly 2018 -03 -16 cwpark 1@kangnung. ac. kr 55

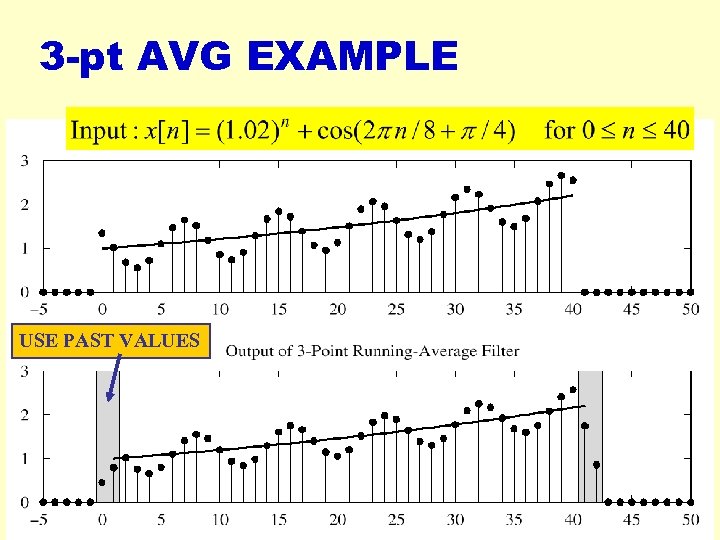3 -pt AVG EXAMPLE USE PAST VALUES 2018 -03 -16 cwpark 1@kangnung. ac. kr 56

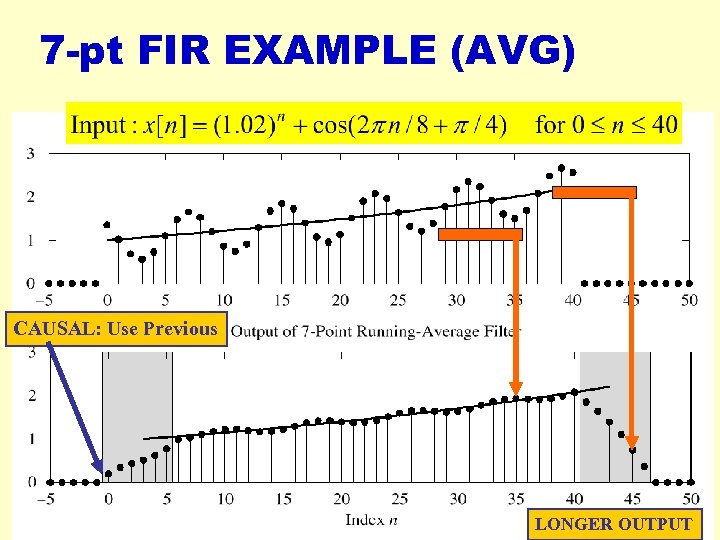7 -pt FIR EXAMPLE (AVG) CAUSAL: Use Previous 2018 -03 -16 cwpark 1@kangnung. ac. kr 57 LONGER OUTPUT