Signal Processing First Lecture 10 Filtering Intro 3 16 2018

Signal Processing First Lecture 10 Filtering Intro 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 1

READING ASSIGNMENTS § This Lecture: § Chapter 5, Sects. 5 -1, 5 -2 and 5 -3 (partial) § Other Reading: § Recitation: Ch. 5, Sects 5 -4, 5 -6, 5 -7 and 5 -8 § CONVOLUTION § Next Lecture: Ch 5, Sects. 5 -3, 5 -5 and 5 -6 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 2

LECTURE OBJECTIVES § INTRODUCE FILTERING IDEA § Weighted Average § Running Average § FINITE IMPULSE RESPONSE FILTERS § FIR Filters § Show to compute the output y[n] from the input signal, x[n] 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 3

DIGITAL FILTERING x(t) A-to-D x[n] COMPUTER y[n] D-to-A y(t) § CONCENTRATE on the COMPUTER § PROCESSING ALGORITHMS § SOFTWARE (MATLAB) § HARDWARE: DSP chips, VLSI § DSP: DIGITAL SIGNAL PROCESSING 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 4

The TMS 32010, 1983 First PC plug-in board from Atlanta Signal Processors Inc. 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 5

Rockland Digital Filter, 1971 For the price of a small house, you could have one of these. 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 6

Digital Cell Phone (ca. 2000) 3/16/2018 Now JH Mc. Clellan & RW Schafer it plays video © 2003, 7

DISCRETE-TIME SYSTEM x[n] COMPUTER y[n] § OPERATE on x[n] to get y[n] § WANT a GENERAL CLASS of SYSTEMS § ANALYZE the SYSTEM § TOOLS: TIME-DOMAIN & FREQUENCY-DOMAIN § SYNTHESIZE the SYSTEM 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 8

D-T SYSTEM EXAMPLES x[n] SYSTEM y[n] § EXAMPLES: § POINTWISE OPERATORS § SQUARING: y[n] = (x[n])2 § RUNNING AVERAGE § RULE: “the output at time n is the average of three consecutive input values” 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 9

DISCRETE-TIME SIGNAL § x[n] is a LIST of NUMBERS § INDEXED by “n” STEM PLOT 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 10

3 -PT AVERAGE SYSTEM § ADD 3 CONSECUTIVE NUMBERS § Do this for each “n” Make a TABLE n=0 3/16/2018 n=1 © 2003, JH Mc. Clellan & RW Schafer 11

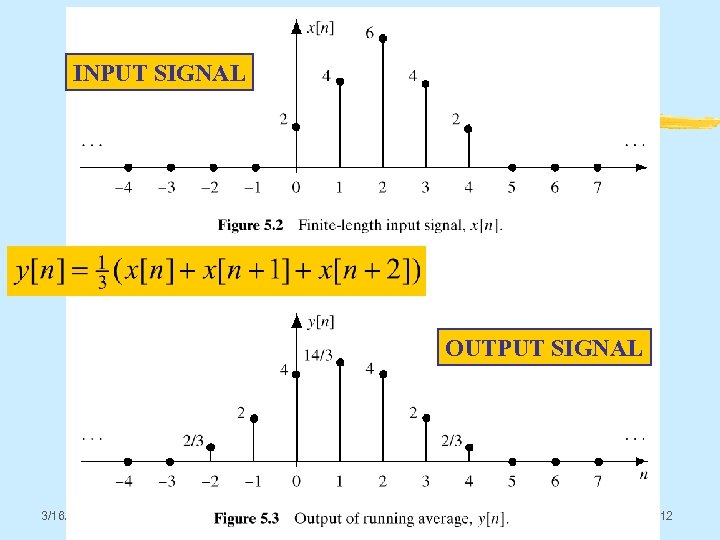INPUT SIGNAL OUTPUT SIGNAL 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 12

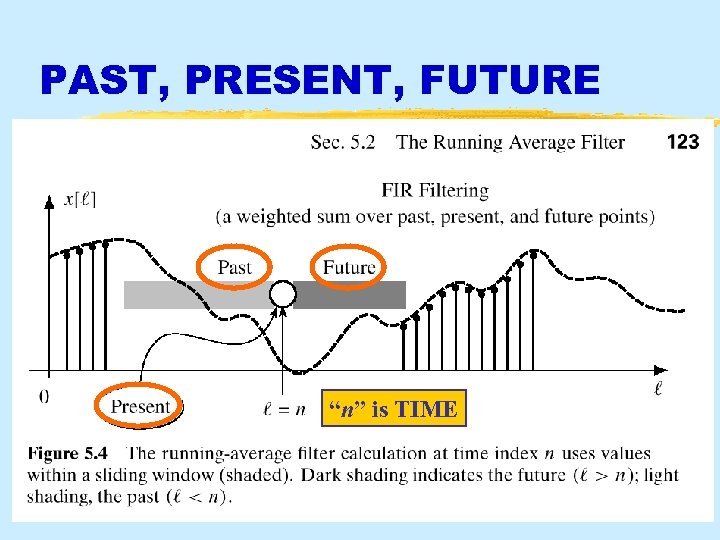PAST, PRESENT, FUTURE “n” is TIME 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 13

ANOTHER 3 -pt AVERAGER § Uses “PAST” VALUES of x[n] § IMPORTANT IF “n” represents REAL TIME § WHEN x[n] & y[n] ARE STREAMS 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 14

GENERAL FIR FILTER § FILTER COEFFICIENTS {bk} § DEFINE THE FILTER § For example, 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 15

GENERAL FIR FILTER § FILTER COEFFICIENTS {bk} § FILTER ORDER is M § FILTER LENGTH is L = M+1 § NUMBER of FILTER COEFFS is L 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 16

GENERAL FIR FILTER § SLIDE a WINDOW across x[n] 3/16/2018 x[n-M] x[n] © 2003, JH Mc. Clellan & RW Schafer 17

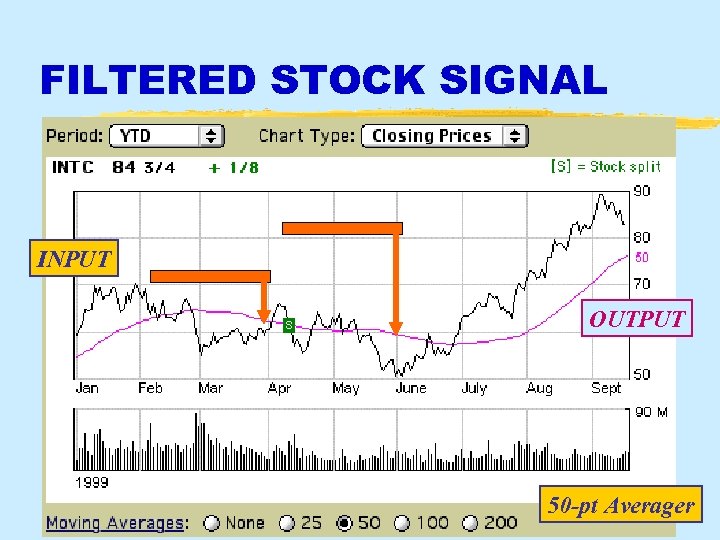FILTERED STOCK SIGNAL INPUT OUTPUT 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 50 -pt Averager 18

SPECIAL INPUT SIGNALS § x[n] = SINUSOID FREQUENCY RESPONSE (LATER) § x[n] has only one NON-ZERO VALUE UNIT-IMPULSE 1 n 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 19

UNIT IMPULSE SIGNAL d[n] is NON-ZERO When its argument is equal to ZERO 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 20

MATH FORMULA for x[n] § Use SHIFTED IMPULSES to write x[n] 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 21

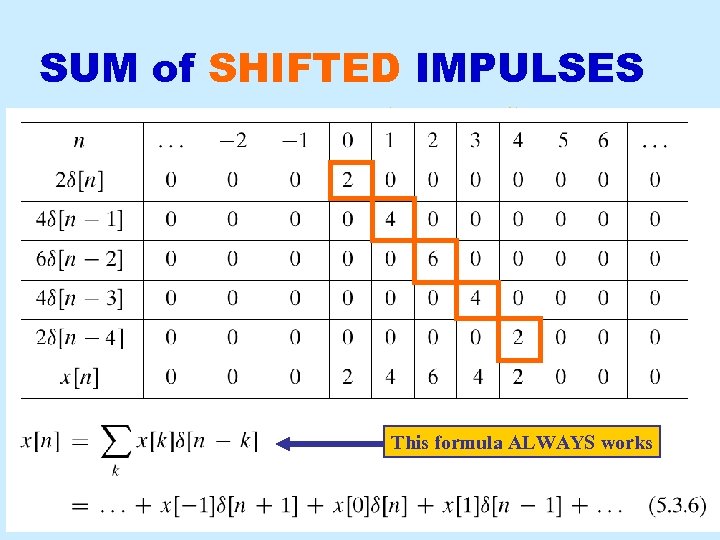SUM of SHIFTED IMPULSES This formula ALWAYS works 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 22

4 -pt AVERAGER § CAUSAL SYSTEM: USE PAST VALUES § INPUT = UNIT IMPULSE SIGNAL = d[n] § OUTPUT is called “IMPULSE RESPONSE” 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 23

4 -pt Avg Impulse Response d[n] “READS OUT” the FILTER COEFFICIENTS “h” in h[n] denotes Impulse Response n=0 n=– 1 n=0 NON-ZERO When window overlaps d[n] 1 n=1 n n=4 n=5 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 24

FIR IMPULSE RESPONSE § Convolution = Filter Definition § Filter Coeffs = Impulse Response CONVOLUTION 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 25

FILTERING EXAMPLE § 7 -point AVERAGER § Smooth compared to 3 -point Averager § By making its amplitude (A) smaller § 3 -point AVERAGER § Changes A slightly 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 26

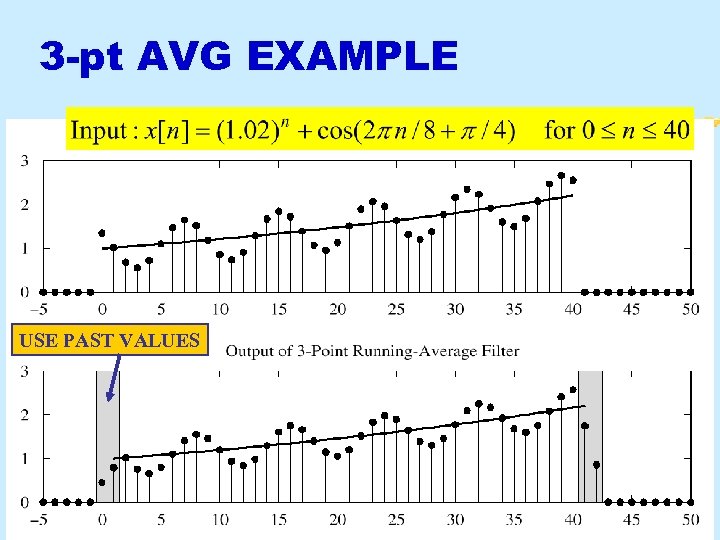3 -pt AVG EXAMPLE USE PAST VALUES 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 27

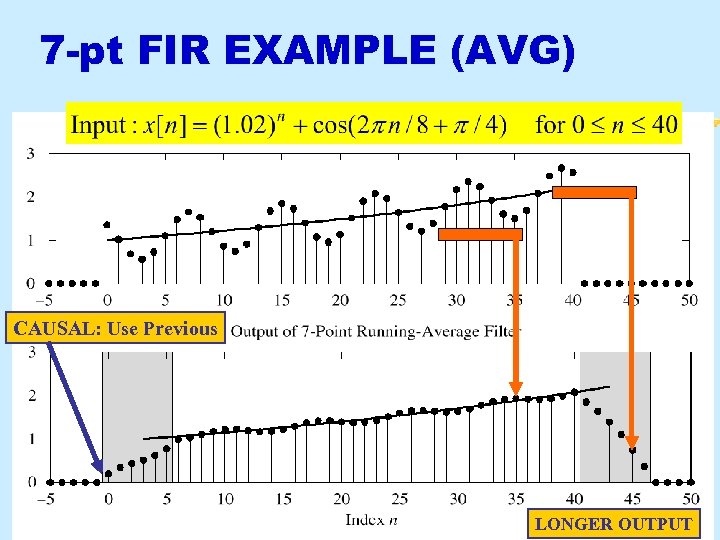7 -pt FIR EXAMPLE (AVG) CAUSAL: Use Previous 3/16/2018 © 2003, JH Mc. Clellan & RW Schafer 28 LONGER OUTPUT