SI Units Mega kilo Units milli micro nano

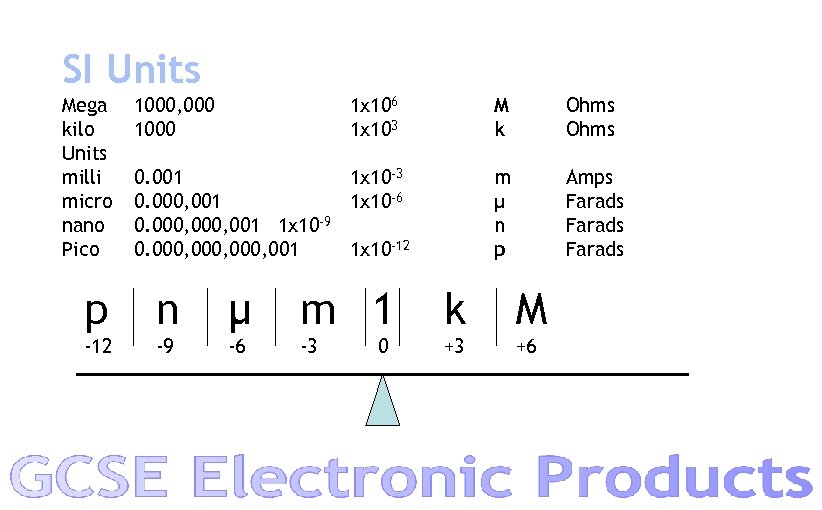SI Units Mega kilo Units milli micro nano Pico 1000, 000 1 x 106 1 x 103 M k m μ n p 0. 001 1 x 10 -3 0. 000, 001 1 x 10 -6 0. 000, 001 1 x 10 -9 0. 000, 001 1 x 10 -12 Ohms Amps Farads p n μ m 1 k M -12 -9 -6 -3 +3 +6 0

SI Units Some shortcuts k x m = cancel out M x μ = cancel out Kxμ=m 1/k = m 1/M = μ M/k = k k/m = M am x an = am+n am / an = am-n

Worked Examples What current flows through a 1 MΩ Resistor when a voltage of 9 V is applied across it? I = = = V/R 9 V/1 MΩ 9/(1 x 106) Amps 9 x 10 -6 Amps 9 μA am x an = am+n am / an = am-n

Worked Examples What is the time constant for an RC network of a 220μf capacitor and 3 k 3 resistor? t = = = Cx. R 220μf x 3 k 3 220 x 3. 3 x (10 -6 x 103) 726 x (10 -3) 0. 73 s am x an = am+n am / an = am-n

Practice Questions a)R=180 kΩ V=9 V b)R=3 M 3ΩV=6 V I=? c)R=100Ω V=3 V d)R=1 MΩ C=220μf e)R=56 kΩ C=330 pf f) R=390 kΩ C=1000μf I = V/R I=? 0. 05 m. A 1. 82μA I=? 30 m. A t=? 220 s t=? 18. 5 ms t=? 390 s t = Cx. R

Practice Questions I=V/R = 9 / 180 k = 9 / 180 x 10 -3 = 0. 05 m. A I=V/R = 6 / 3 M 3 = 6 / 3. 3 x 10 -6 = 1. 82 μA I=V/R = 3 / 100 = 0. 03 A = 30 m. A t = Cx. R = 220μf x 1 M = 220 x 1 x (10 -6 x 106) = 220 x (100) = 220 s t = Cx. R = 330 pf x 56 k = 330 x 56 x (10 -12 x 103) = 18480 x (10 -9) = 18. 5 x(10 -6) = 18. 5 μs t = Cx. R = 1000μf x 390 k = 1000 x 390 x (10 -6 x 103) = 390000 x (10 -3) = 390 x (103 x 10 -3) = 390 s

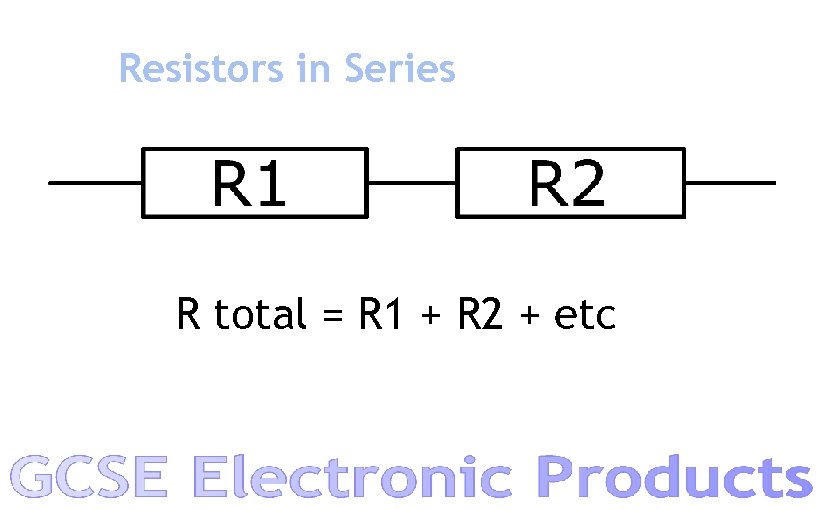Resistors in Series R total = R 1 + R 2 + etc

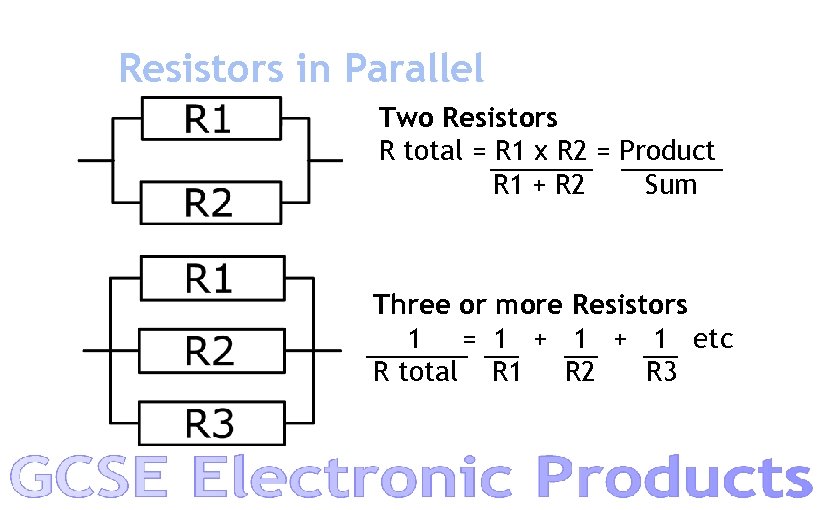Resistors in Parallel Two Resistors R total = R 1 x R 2 = Product R 1 + R 2 Sum Three or more Resistors 1 = 1 + 1 etc R total R 1 R 2 R 3

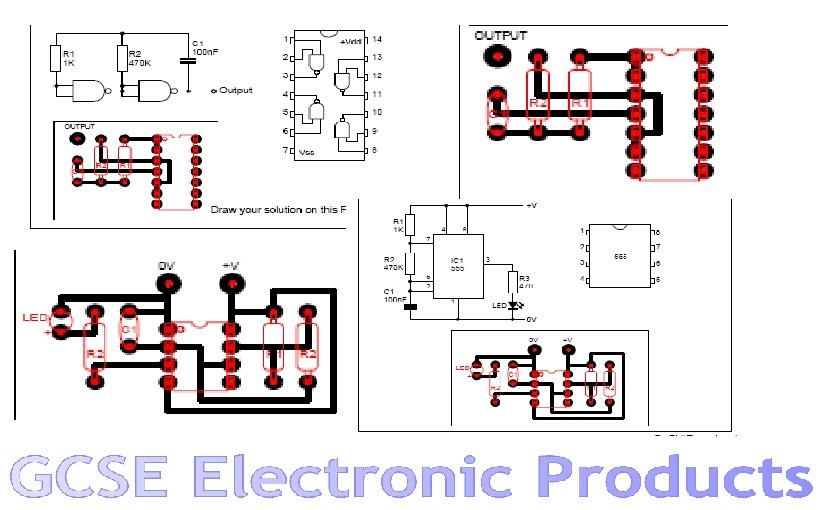
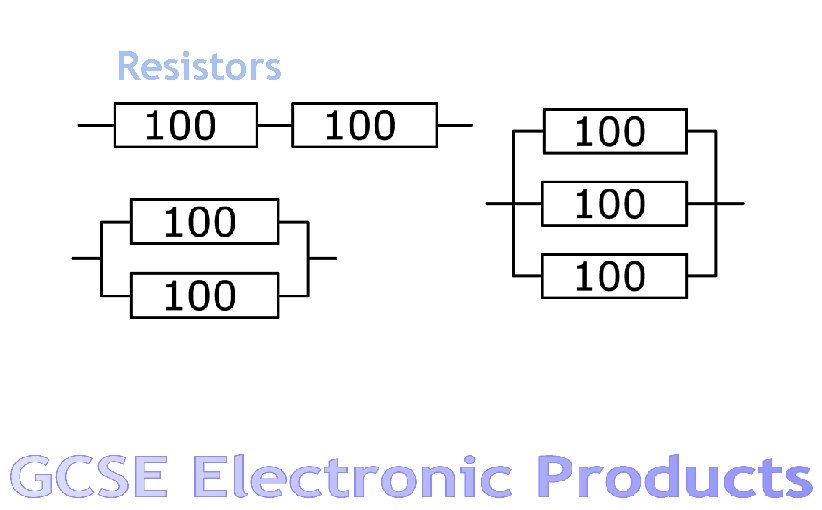Resistors

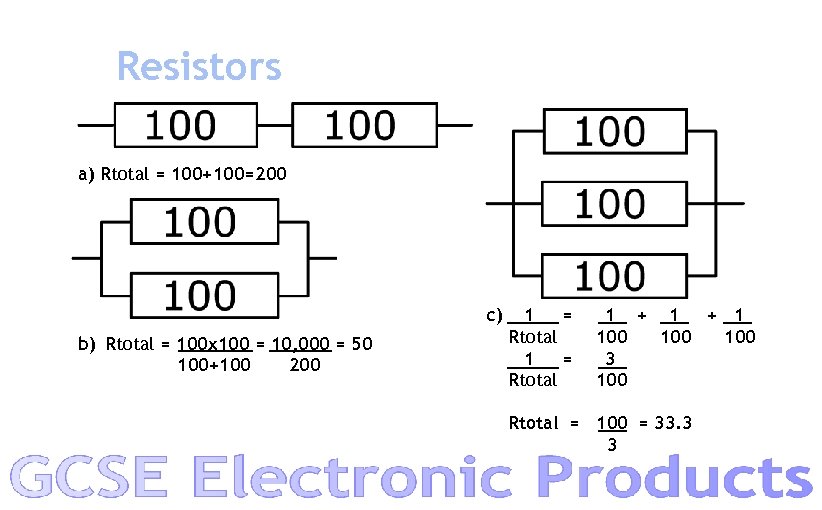Resistors a) Rtotal = 100+100=200 c) b) Rtotal = 100 x 100 = 10, 000 = 50 100+100 200 1 = Rtotal 1 + 1 100 100 3 100 Rtotal = 100 = 33. 3 3

Ohms Law

Worked Examples What current flows through a 1 MΩ Resistor when a voltage of 9 V is applied across it? I = = = V/R 9 V/1 MΩ 9/(1 x 106) Amps 9 x 10 -6 Amps 9 μA am x an = am+n am / an = am-n

Voltage Divider Vout = R 2 x Vsupply R 1+R 2 When resistors are in series voltage is split in the same ratio as the resistance. A voltage divider uses this to give a specified output (Vs). This equates to the value of R 2 divided by the total resistance, times by the supply voltage. Worked Example, V=9 V, R 1=3 k 3, R 2=6 k 9

Worked Example (In the exam, copy out the equation first) Vs = 6 k 9 x 9 V (3 k 3 + 6 k 9) = 6, 900 x 9 V 10, 200 = 6. 08 V

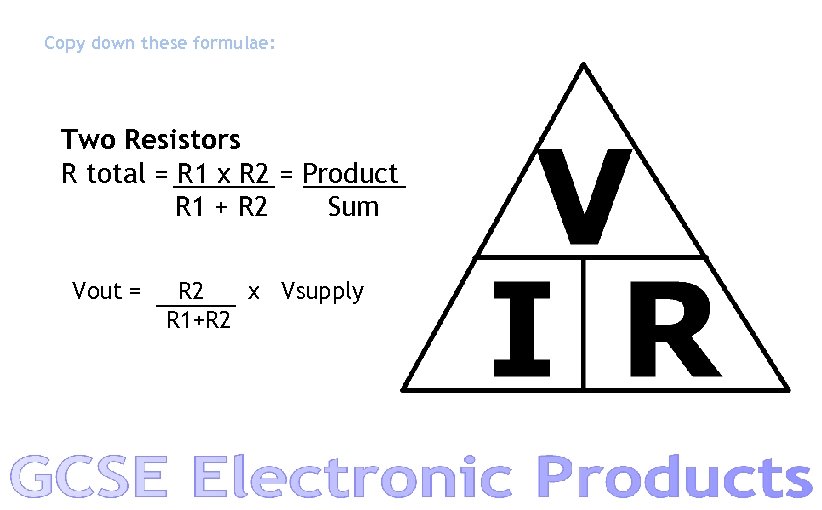Copy down these formulae: Two Resistors R total = R 1 x R 2 = Product R 1 + R 2 Sum Vout = R 2 x Vsupply R 1+R 2

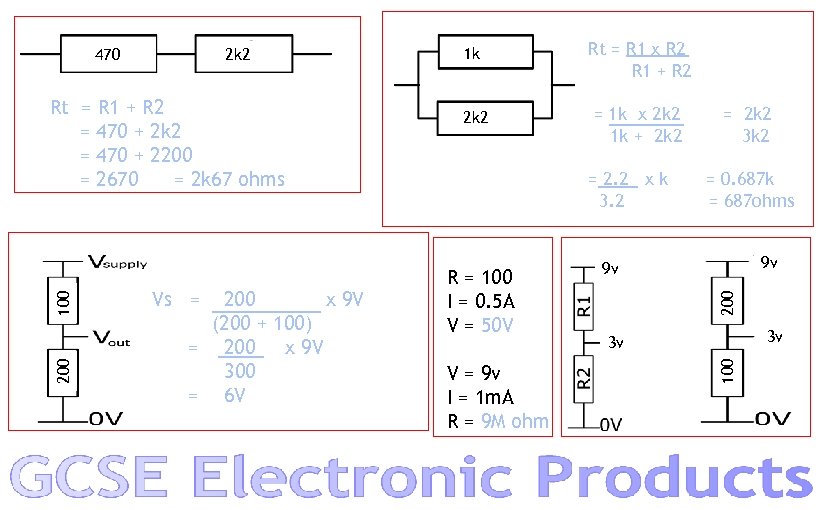200 100 Rt = R 1 + R 2 = 470 + 2 k 2 = 470 + 2200 = 2670 = 2 k 67 ohms Vs = 200 x 9 V (200 + 100) = 200 x 9 V 300 = 6 V 1 k Rt = R 1 x R 2 R 1 + R 2 2 k 2 = 1 k x 2 k 2 1 k + 2 k 2 = 2. 2 x k 3. 2 R = 100 I = 0. 5 A V = 50 V V = 9 v I = 1 m. A R = 9 M ohm = 2 k 2 3 k 2 = 0. 687 k = 687 ohms 9 v 9 v 200 2 k 2 3 v 3 v 100 470

Capacitors

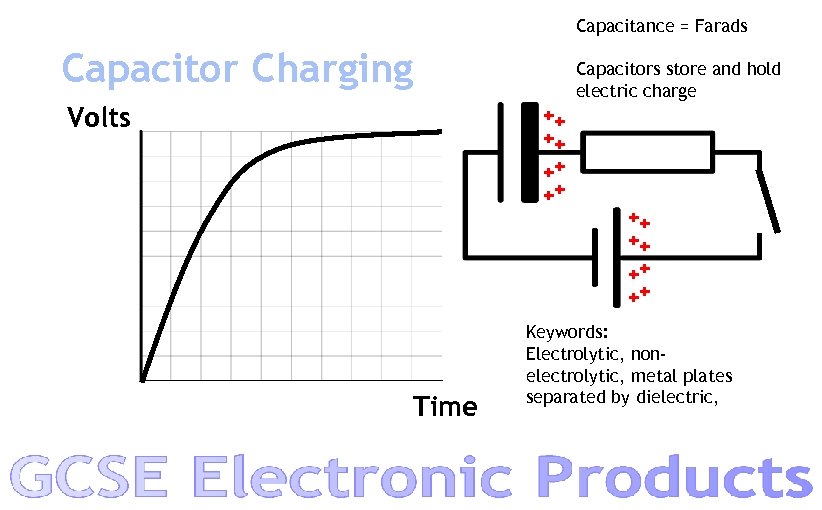Capacitance = Farads Capacitor Charging Volts Capacitors store and hold electric charge ++ ++ Time Keywords: Electrolytic, nonelectrolytic, metal plates separated by dielectric,

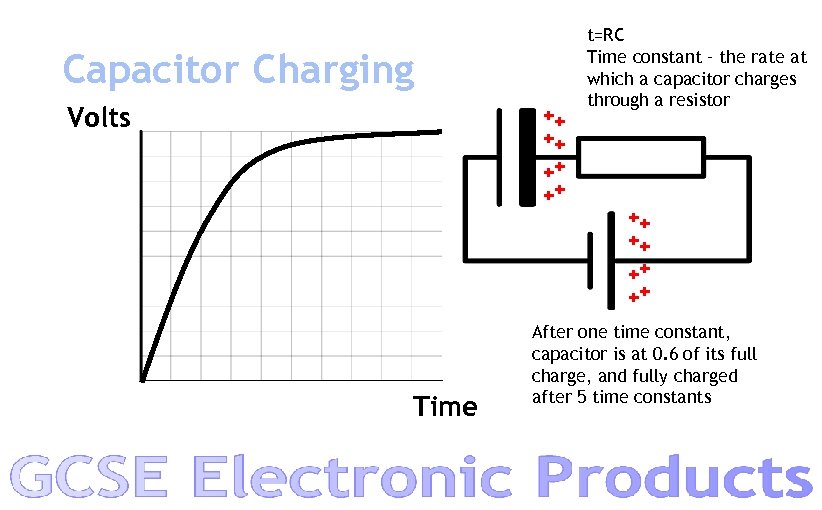Capacitor Charging Volts ++ ++ t=RC Time constant – the rate at which a capacitor charges through a resistor ++ ++ Time After one time constant, capacitor is at 0. 6 of its full charge, and fully charged after 5 time constants

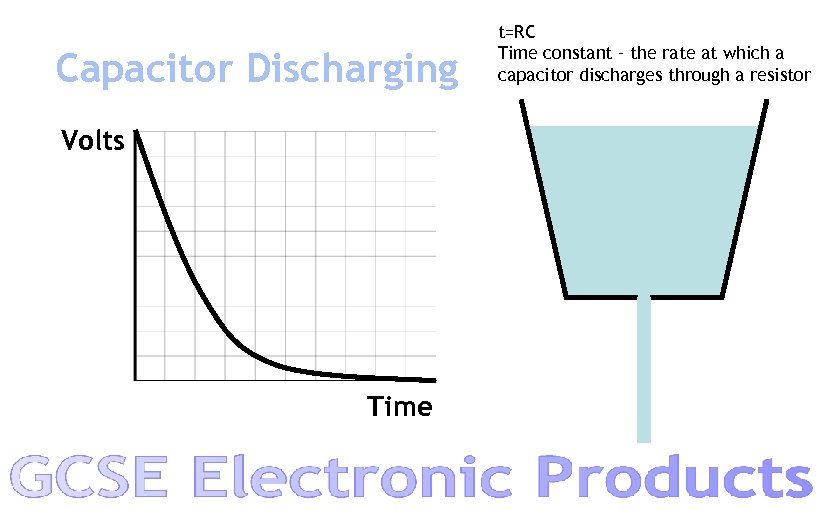Capacitor Discharging Volts Time t=RC Time constant – the rate at which a capacitor discharges through a resistor

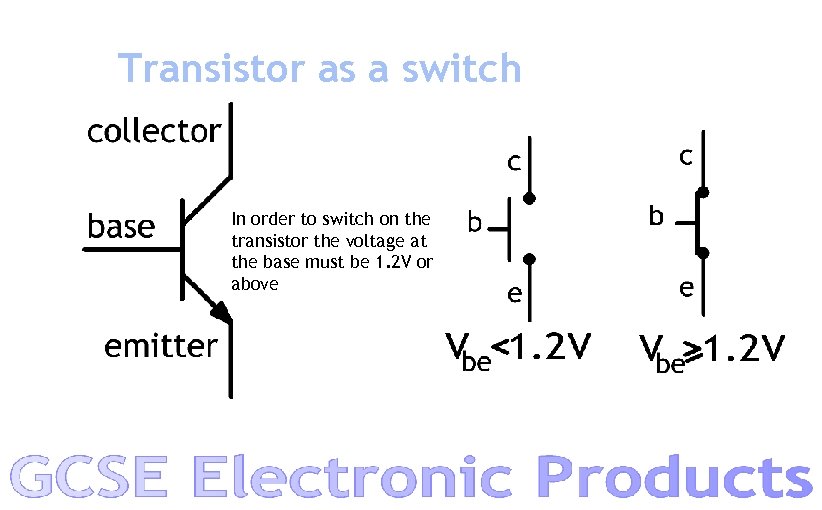Transistor as a switch In order to switch on the transistor the voltage at the base must be 1. 2 V or above

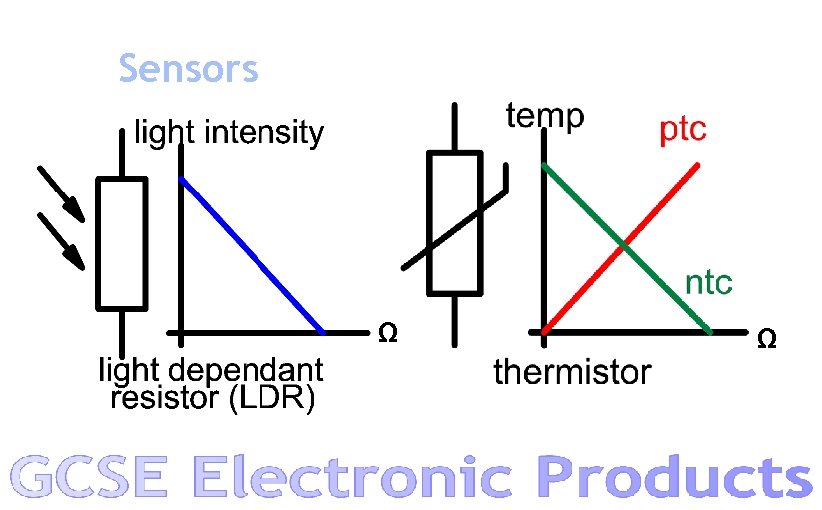Sensors Ω Ω

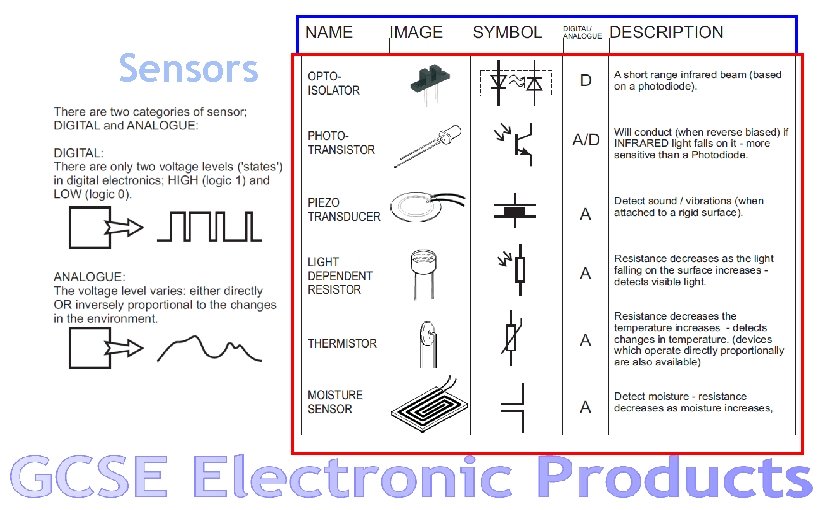Sensors

Voltage Dividers as Sensors Vout = R 2 x Vsupply R 1+R 2 So, if R 2 >> R 1, Vout is close to Vsupply

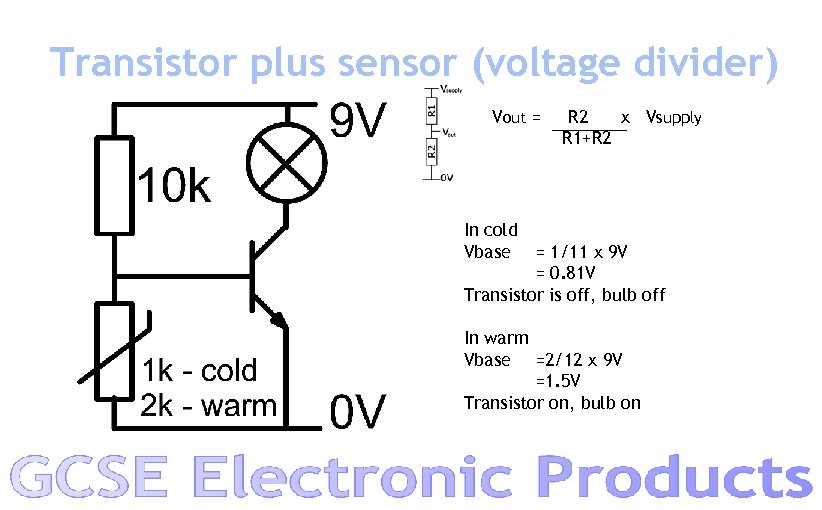Transistor plus sensor (voltage divider) Vout = R 2 x Vsupply R 1+R 2 In cold Vbase = 1/11 x 9 V = 0. 81 V Transistor is off, bulb off In warm Vbase =2/12 x 9 V =1. 5 V Transistor on, bulb on

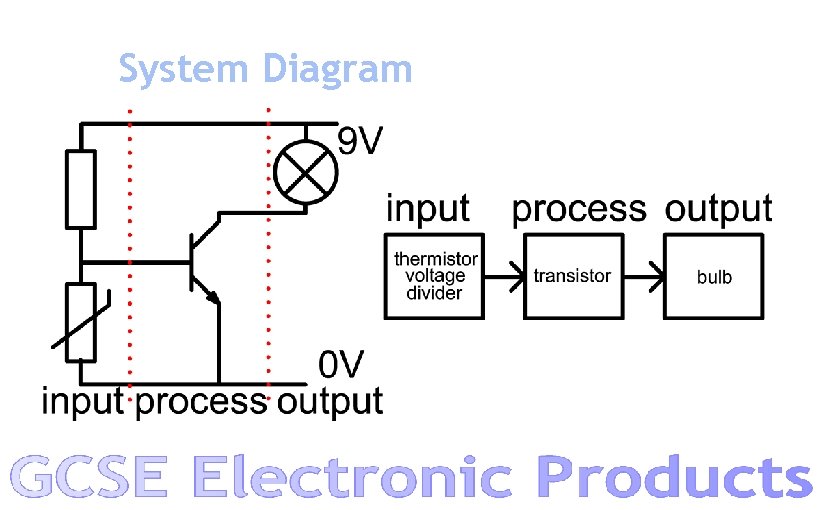System Diagram

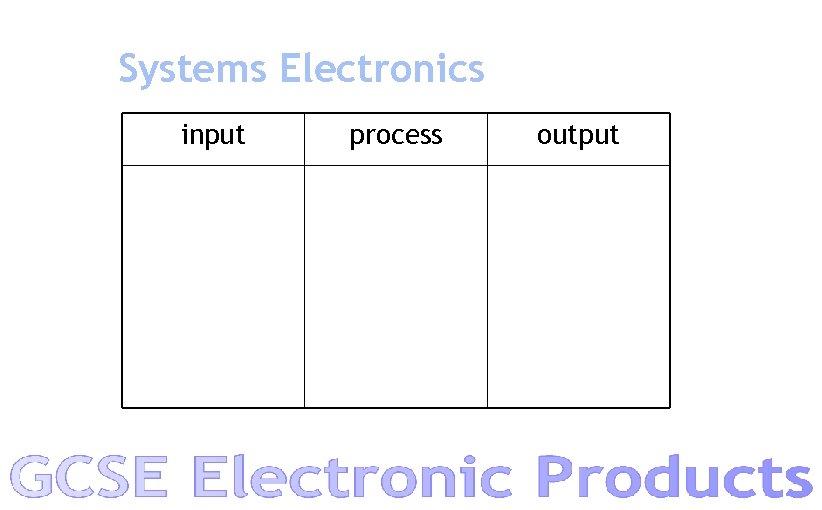Systems Electronics input process output

Systems Electronics input Switch LDR Thermistor Moisture Sensor Variable Resistor Microphone Piezo process Transistor Delay Oscillator Counter Latch Amplifier Comparator Logic Gates PIC output Buzzer Speaker Bulb LED Motor Relay Solenoid Piezo

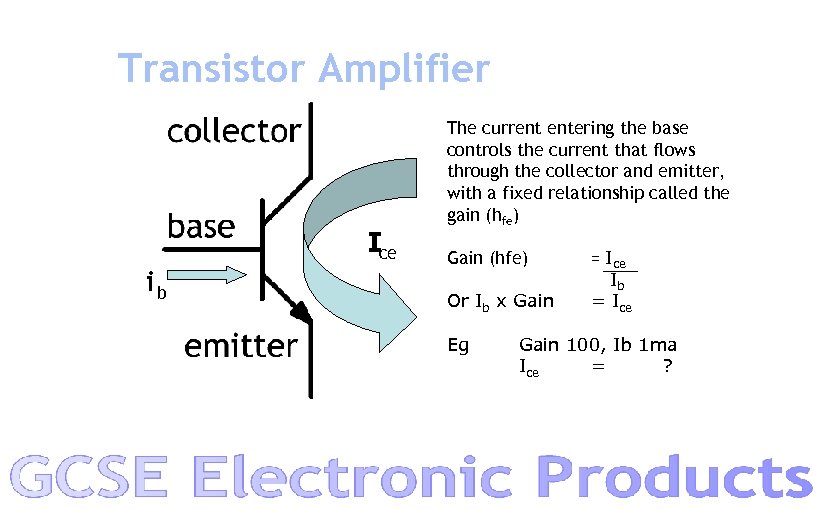Transistor Amplifier Ice ib The current entering the base controls the current that flows through the collector and emitter, with a fixed relationship called the gain (hfe) Gain (hfe) Or Ib x Gain Eg = Ice Ib = Ice Gain 100, Ib 1 ma Ice = ?

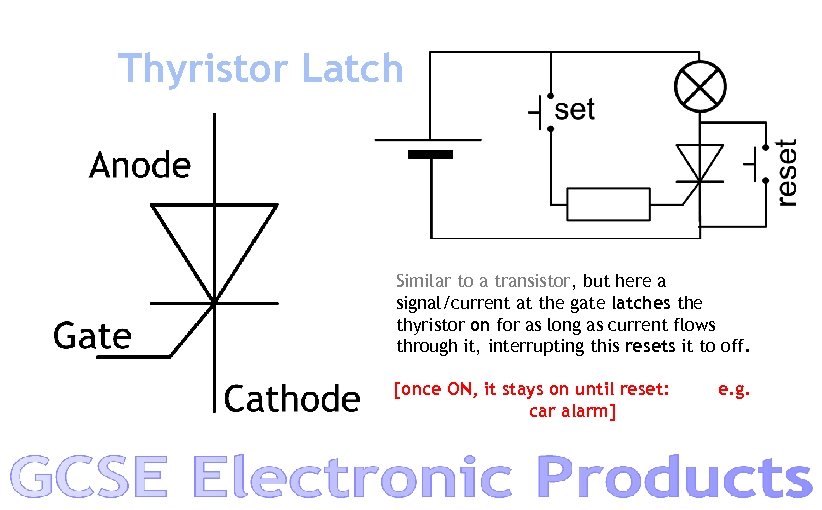Thyristor Latch Similar to a transistor, but here a signal/current at the gate latches the thyristor on for as long as current flows through it, interrupting this resets it to off. [once ON, it stays on until reset: car alarm] e. g.

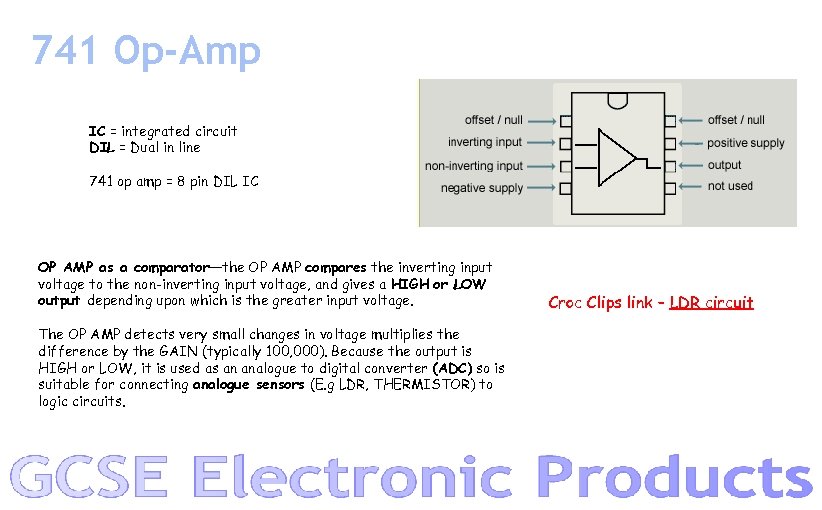741 Op-Amp IC = integrated circuit DIL = Dual in line 741 op amp = 8 pin DIL IC OP AMP as a comparator—the OP AMP compares the inverting input voltage to the non-inverting input voltage, and gives a HIGH or LOW output depending upon which is the greater input voltage. The OP AMP detects very small changes in voltage multiplies the difference by the GAIN (typically 100, 000). Because the output is HIGH or LOW, it is used as an analogue to digital converter (ADC) so is suitable for connecting analogue sensors (E. g LDR, THERMISTOR) to logic circuits. Croc Clips link – LDR circuit

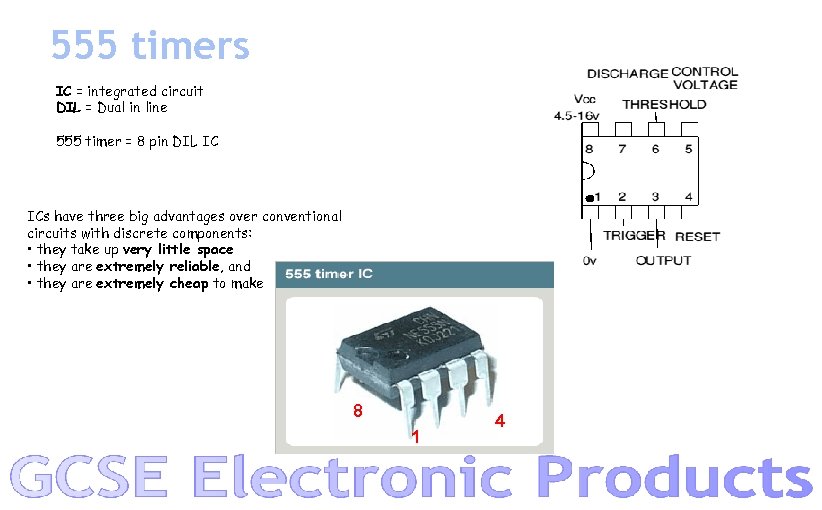555 timers IC = integrated circuit DIL = Dual in line 555 timer = 8 pin DIL IC ICs have three big advantages over conventional circuits with discrete components: • they take up very little space • they are extremely reliable, and • they are extremely cheap to make 8 1 4

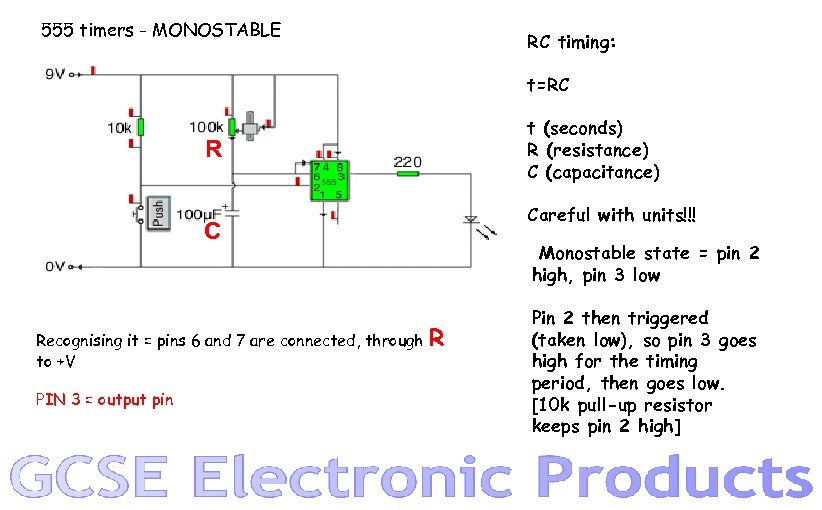555 timers - MONOSTABLE RC timing: t=RC t (seconds) R (resistance) C (capacitance) R Careful with units!!! C Recognising it = pins 6 and 7 are connected, through to +V PIN 3 = output pin Monostable state = pin 2 high, pin 3 low R Pin 2 then triggered (taken low), so pin 3 goes high for the timing period, then goes low. [10 k pull-up resistor keeps pin 2 high]

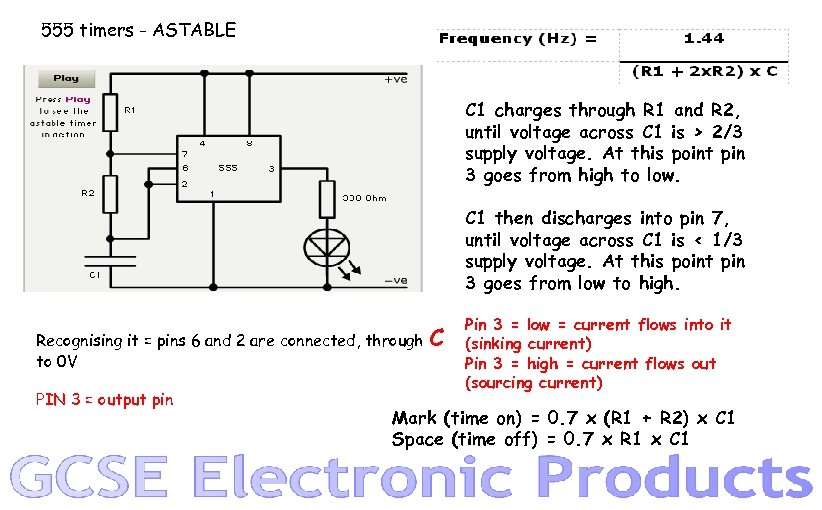555 timers - ASTABLE C 1 charges through R 1 and R 2, until voltage across C 1 is > 2/3 supply voltage. At this point pin 3 goes from high to low. C 1 then discharges into pin 7, until voltage across C 1 is < 1/3 supply voltage. At this point pin 3 goes from low to high. Recognising it = pins 6 and 2 are connected, through to 0 V PIN 3 = output pin C Pin 3 = low = current flows into it (sinking current) Pin 3 = high = current flows out (sourcing current) Mark (time on) = 0. 7 x (R 1 + R 2) x C 1 Space (time off) = 0. 7 x R 1 x C 1

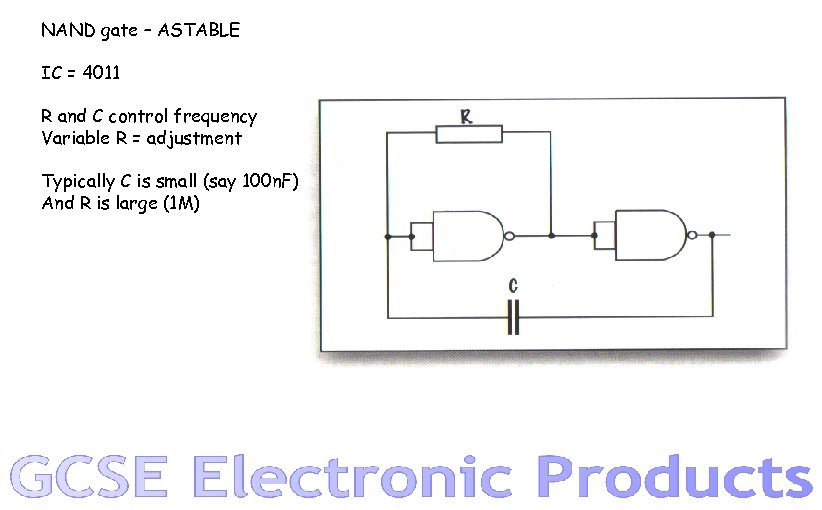NAND gate – ASTABLE IC = 4011 R and C control frequency Variable R = adjustment Typically C is small (say 100 n. F) And R is large (1 M)

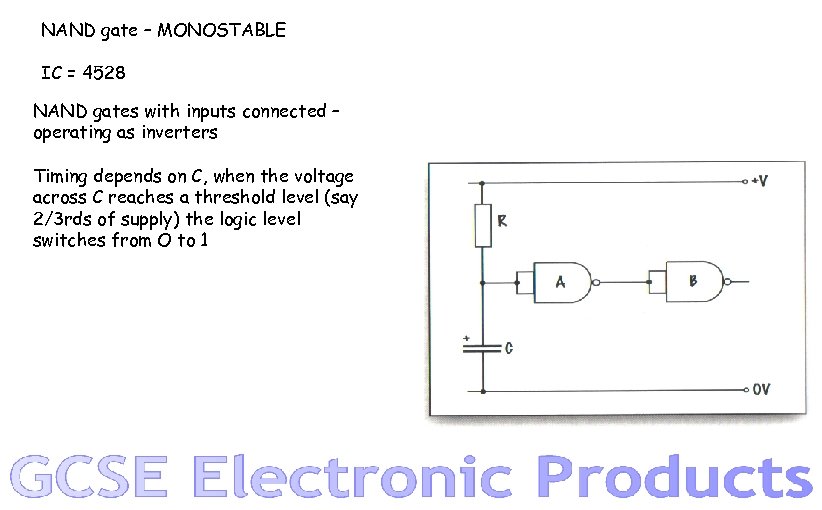NAND gate – MONOSTABLE IC = 4528 NAND gates with inputs connected – operating as inverters Timing depends on C, when the voltage across C reaches a threshold level (say 2/3 rds of supply) the logic level switches from O to 1

Counters 4017 and 4026 data

Some positives… can you say YES to these… Last years group achieved average 81% in their coursework, and 83% A*-C overall YOU have achieved average 81% in their coursework WE have nearly at the end of the revision and course YOU already know enough to achieve A* - C overall This morning YOU will know what to expect in next months exam, and know what to do to perform your best This morning we will study the remaining OUTPUT components and LOGIC

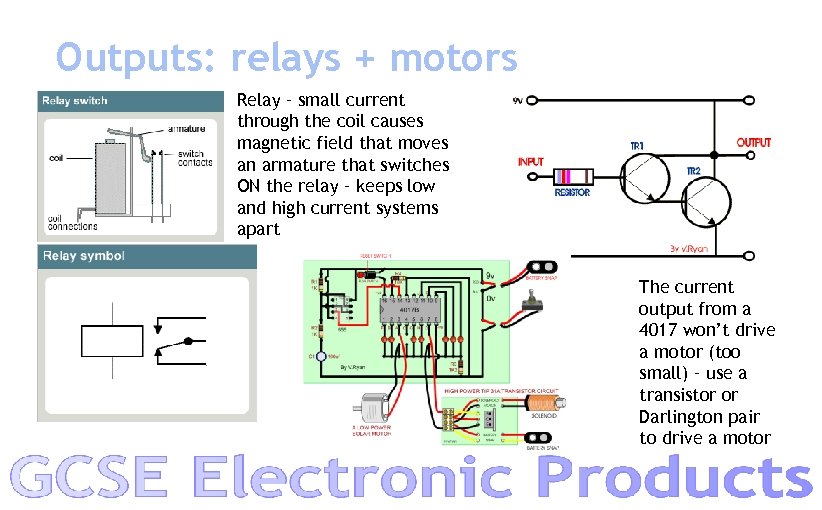Outputs: relays + motors Relay – small current through the coil causes magnetic field that moves an armature that switches ON the relay – keeps low and high current systems apart The current output from a 4017 won’t drive a motor (too small) – use a transistor or Darlington pair to drive a motor

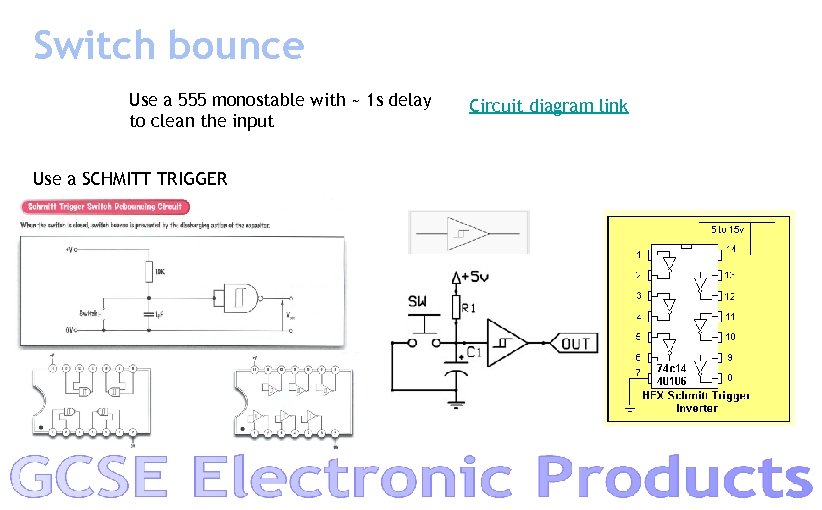Switch bounce Use a 555 monostable with ~ 1 s delay to clean the input Use a SCHMITT TRIGGER Circuit diagram link

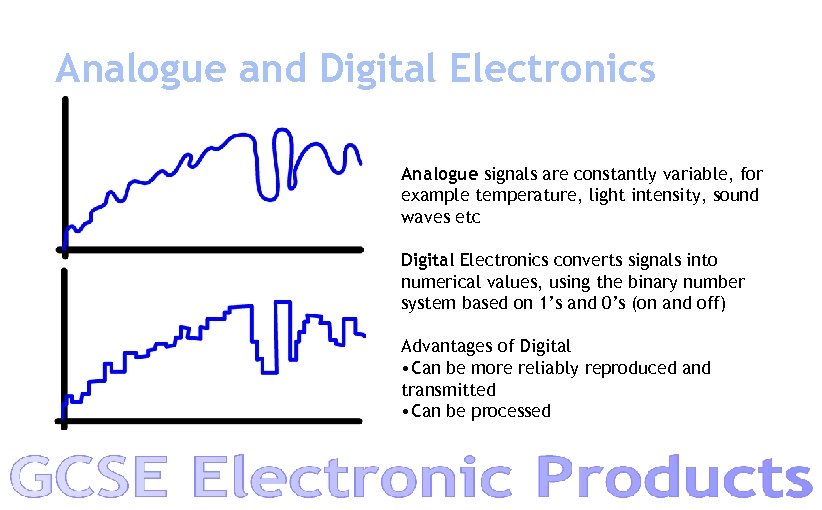Analogue and Digital Electronics Analogue signals are constantly variable, for example temperature, light intensity, sound waves etc Digital Electronics converts signals into numerical values, using the binary number system based on 1’s and 0’s (on and off) Advantages of Digital • Can be more reliably reproduced and transmitted • Can be processed

Binary Numbers A single binary number is called a bit An 8 digit binary number is called a byte, and can represent a decimal number from 0 to 255 128 s 64 s 32 s 16 s 8 s 4 s 2 s units decimal 1 0 1 0 170 0 0 1 1 15 0 1 1 1 127 1 1 1 1 255

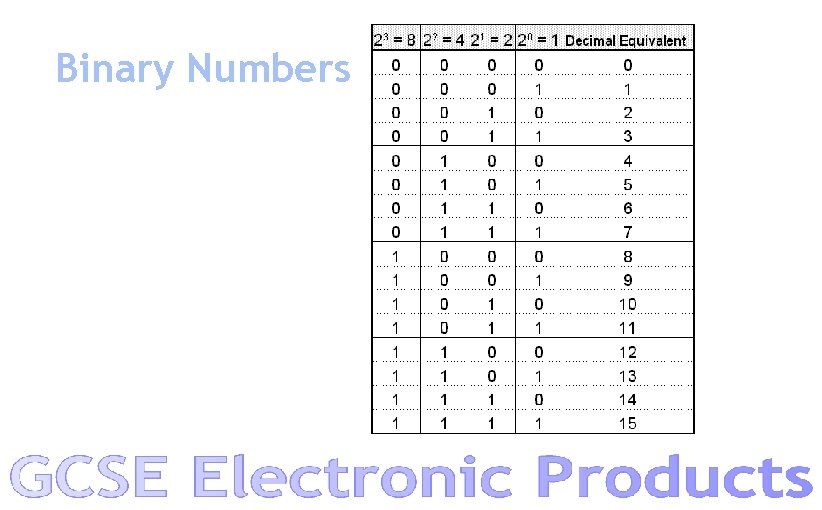Binary Numbers

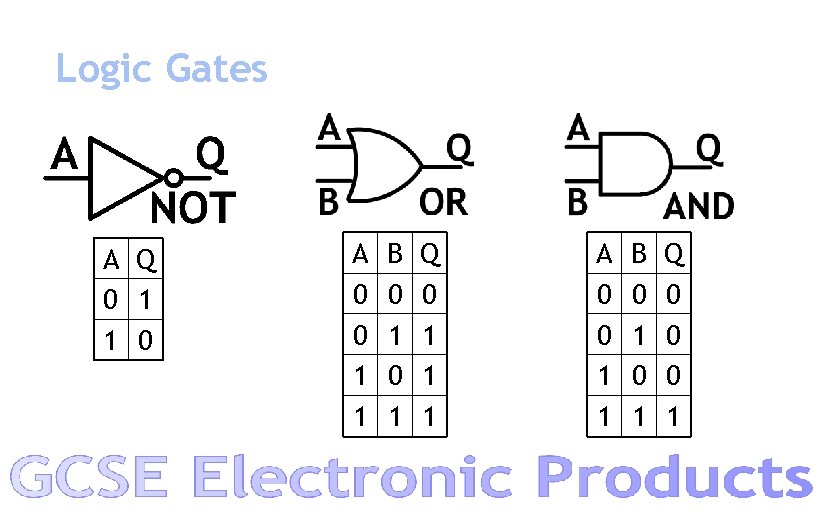Logic Gates A Q 0 1 1 0 A 0 0 1 1 B 0 1 Q 0 1 1 1 A 0 0 1 1 B 0 1 Q 0 0 0 1

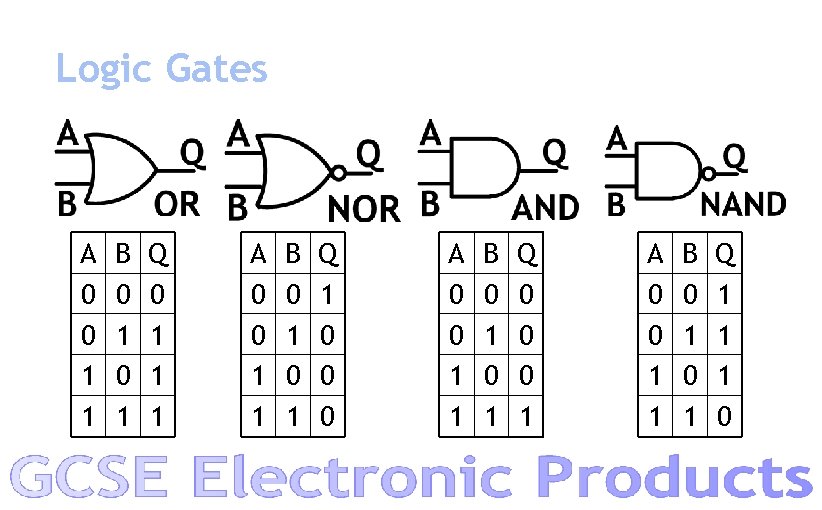Logic Gates A 0 0 1 1 B 0 1 Q 0 1 1 1 A 0 0 1 1 B 0 1 Q 1 0 0 0 A 0 0 1 1 B 0 1 Q 0 0 0 1 A 0 0 1 1 B 0 1 Q 1 1 1 0

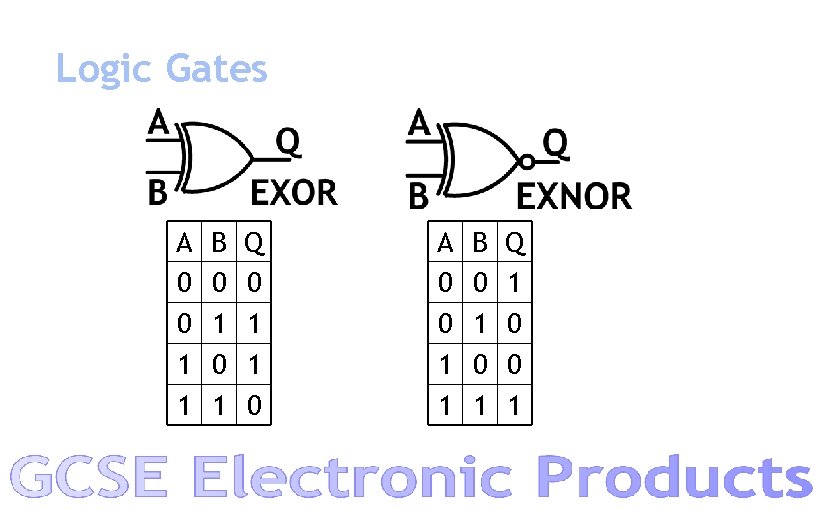Logic Gates A 0 0 1 1 B 0 1 Q 0 1 1 0 A 0 0 1 1 B 0 1 Q 1 0 0 1

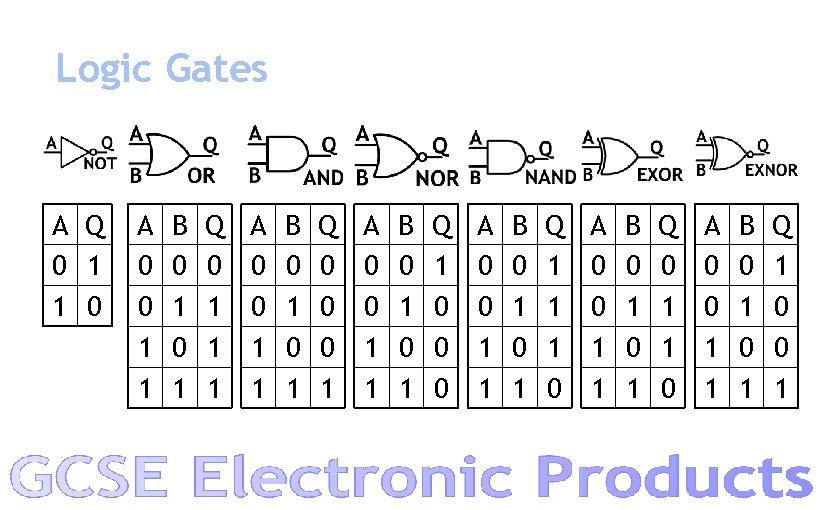Logic Gates A Q 0 1 1 0 A 0 0 1 1 B 0 1 Q 0 1 1 1 A 0 0 1 1 B 0 1 Q 0 0 0 1 A 0 0 1 1 B 0 1 Q 1 0 0 0 A 0 0 1 1 B 0 1 Q 1 1 1 0 A 0 0 1 1 B 0 1 Q 0 1 1 0 A 0 0 1 1 B 0 1 Q 1 0 0 1

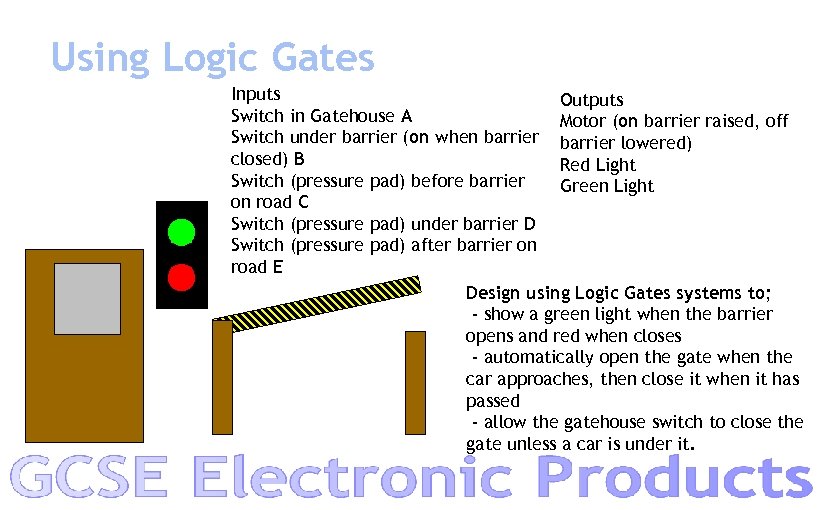Using Logic Gates Inputs Outputs Switch in Gatehouse A Motor (on barrier raised, off Switch under barrier (on when barrier lowered) closed) B Red Light Switch (pressure pad) before barrier Green Light on road C Switch (pressure pad) under barrier D Switch (pressure pad) after barrier on road E Design using Logic Gates systems to; - show a green light when the barrier opens and red when closes - automatically open the gate when the car approaches, then close it when it has passed - allow the gatehouse switch to close the gate unless a car is under it.

PIC Chips Programmable Integrated Circuits Come in various numbers of pins which limit the number of inputs and outputs Easiest way to imagine a pic is like a programmable ‘process block’

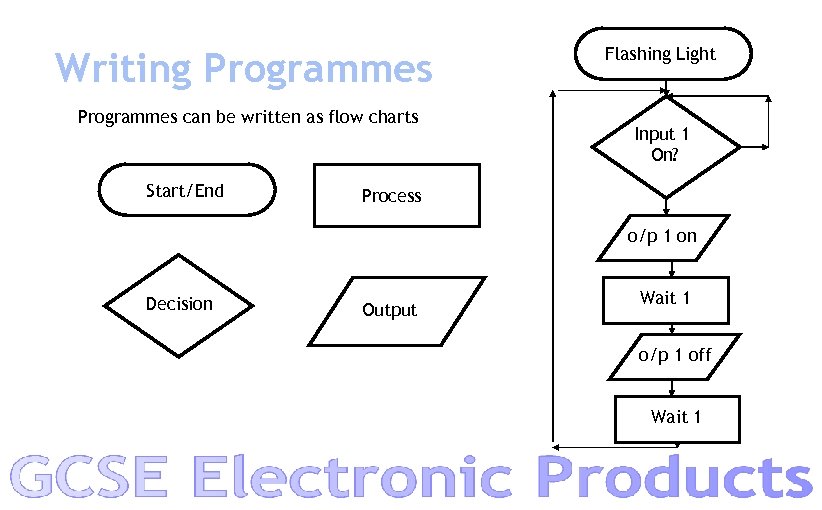Writing Programmes can be written as flow charts Start/End Flashing Light Input 1 On? Process o/p 1 on Decision Output Wait 1 o/p 1 off Wait 1

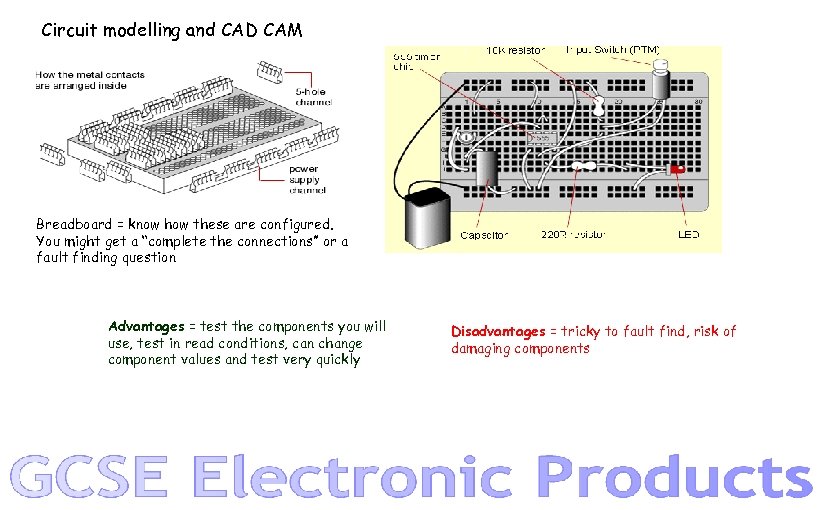Circuit modelling and CAD CAM Breadboard = know how these are configured. You might get a “complete the connections” or a fault finding question Advantages = test the components you will use, test in read conditions, can change component values and test very quickly Disadvantages = tricky to fault find, risk of damaging components

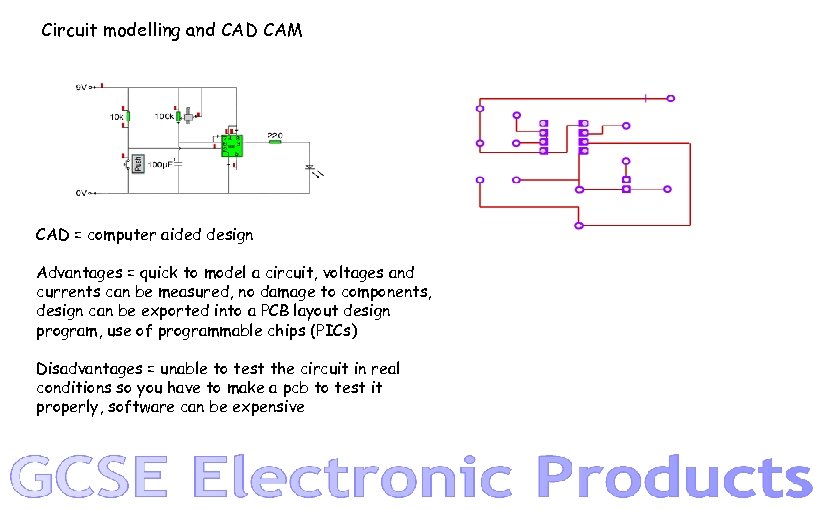Circuit modelling and CAD CAM CAD = computer aided design Advantages = quick to model a circuit, voltages and currents can be measured, no damage to components, design can be exported into a PCB layout design program, use of programmable chips (PICs) Disadvantages = unable to test the circuit in real conditions so you have to make a pcb to test it properly, software can be expensive

CAM = computer aided manufacture • CNC processes to cut and drill PCB’s • pick and place components automatically • digital photography to check (QC) component positions • automated processes e. g wave soldering PCB making: http: //www. youtube. com/watch? v=SKcc. Lh. Ff 1 DY http: //vixy. net/ Or this

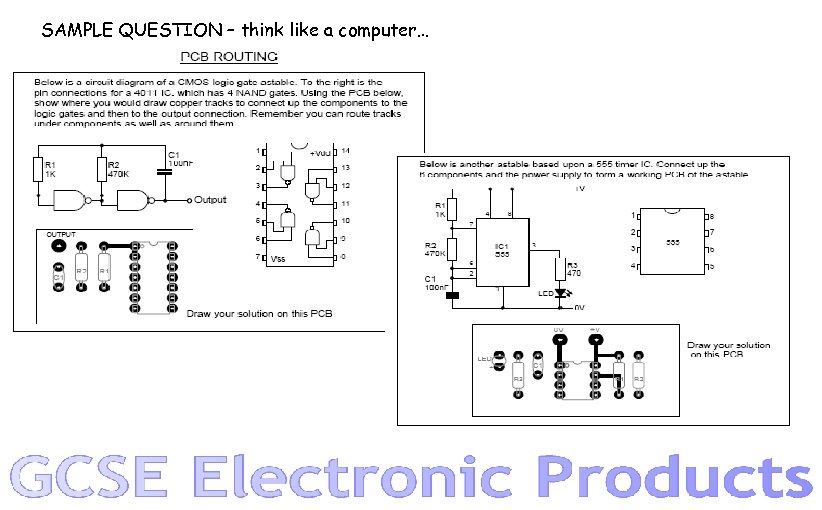SAMPLE QUESTION – think like a computer…