Шулятев Дмитрий Александрович Оптика 1 Волновая оптика 2

Шулятев Дмитрий Александрович Оптика 1. Волновая оптика 2. Квантово-оптические явления 3. Основы квантовой механики. Атомная физика. Ядерная физика

Рекомендуемая литература

Рекомендуемая литература

Тема 1. ВОЛНОВЫЕ ПРОЦЕССЫ Упругие волны • • • Распространение волн в упругой среде Волновой фронт и волновая поверхность Уравнение плоской волны Волновой вектор Волновое уравнение Электромагнитные волны • • Волновое уравнение для электромагнитного поля Световой луч Оптическая длина пути Световая волна на границе раздела сред

Распространение волн в упругой среде Волной или волновым процессом называется распространение в пространстве возмущения вещества и поля, проявляющееся в переносе энергии возмущения

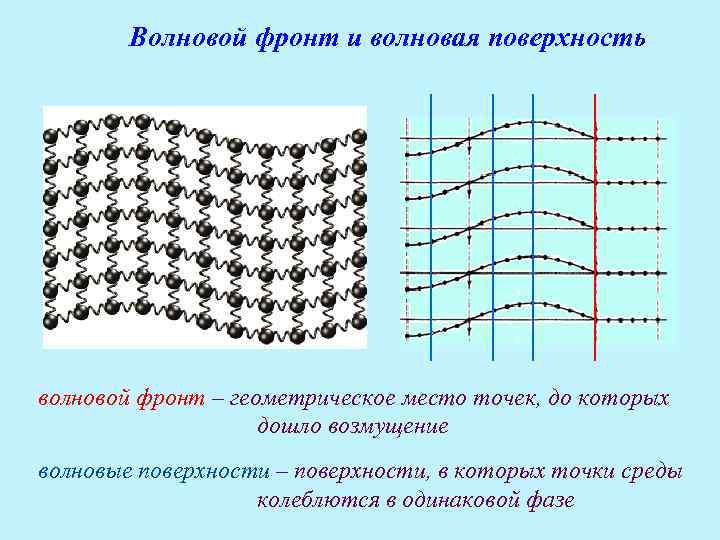Волновой фронт и волновая поверхность волновой фронт – геометрическое место точек, до которых дошло возмущение волновые поверхности – поверхности, в которых точки среды колеблются в одинаковой фазе

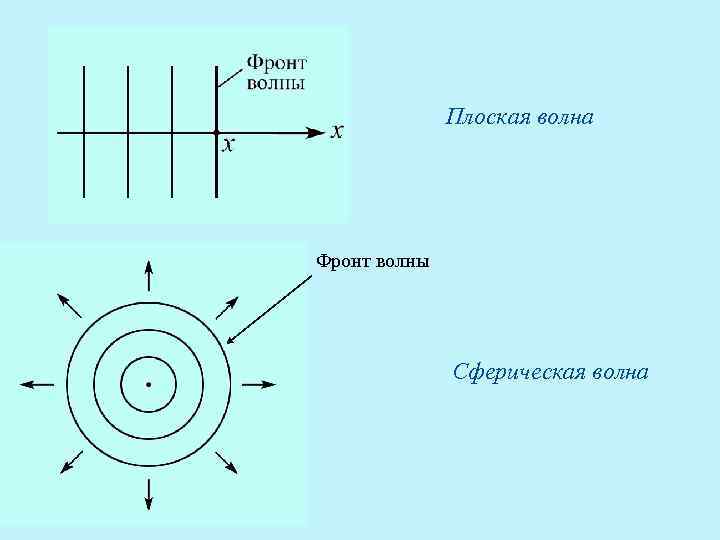Плоская волна Фронт волны Сферическая волна

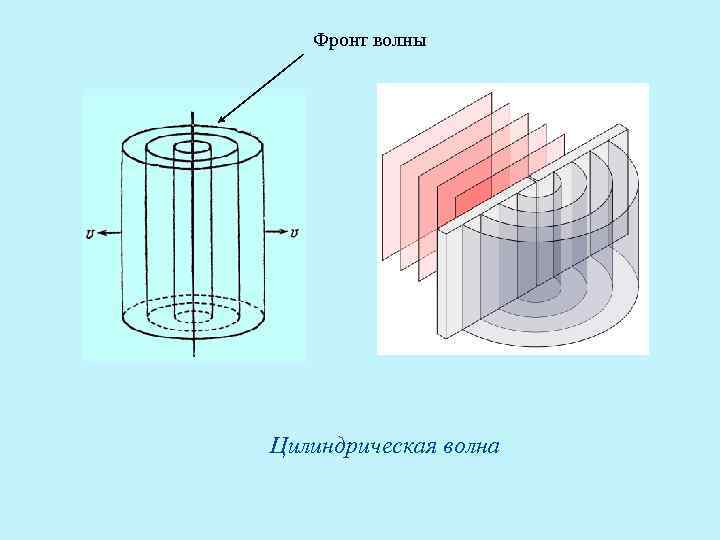Фронт волны Цилиндрическая волна

Поперечная волна Продольная волна плоская волна

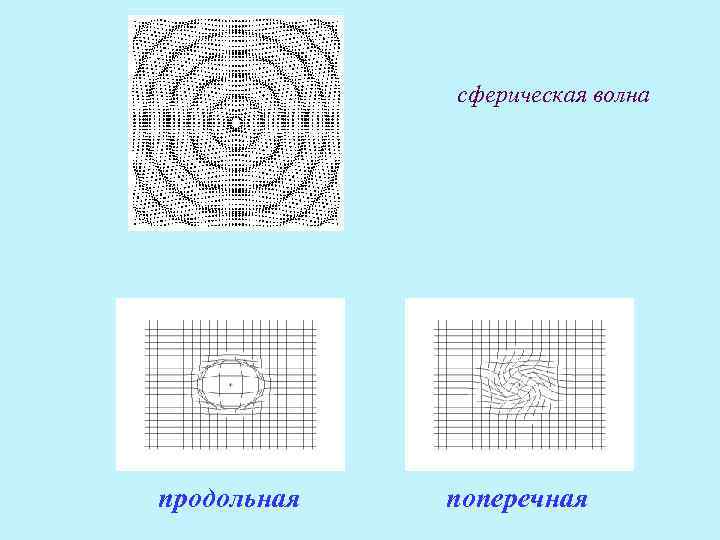сферическая волна продольная поперечная

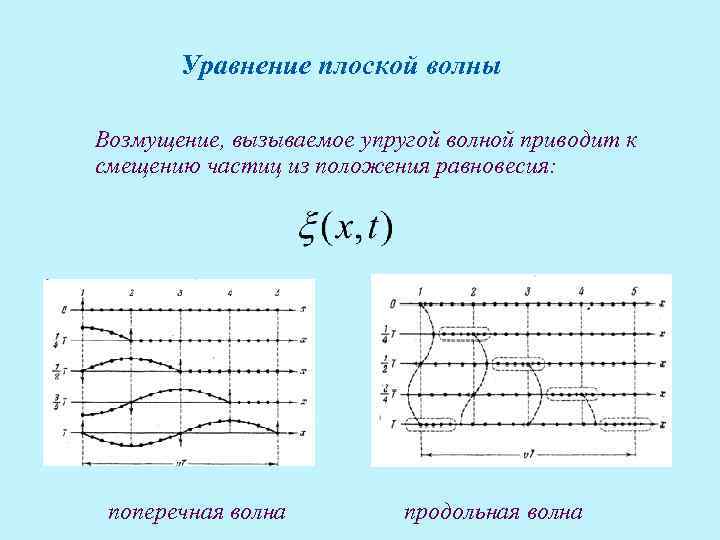Уравнение плоской волны Возмущение, вызываемое упругой волной приводит к смещению частиц из положения равновесия: поперечная волна продольная волна

Гармонический осциллятор ξmax -ξmax А - амплитуда ω – циклическая (круговая) частота

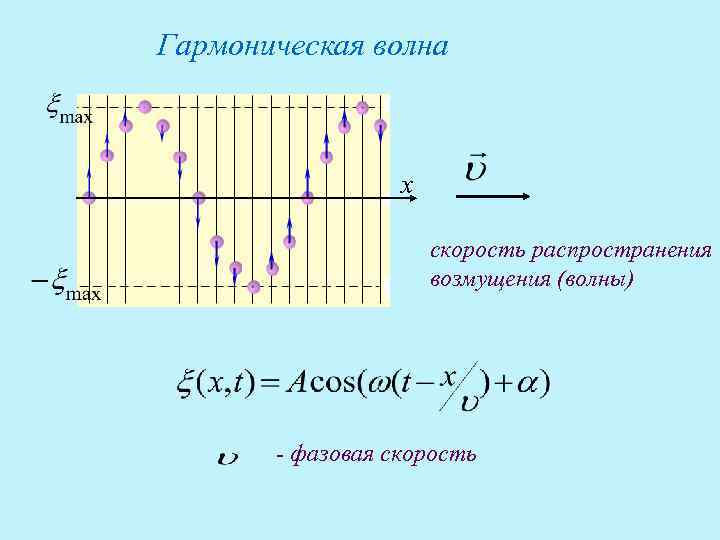Гармоническая волна x скорость распространения возмущения (волны) - фазовая скорость

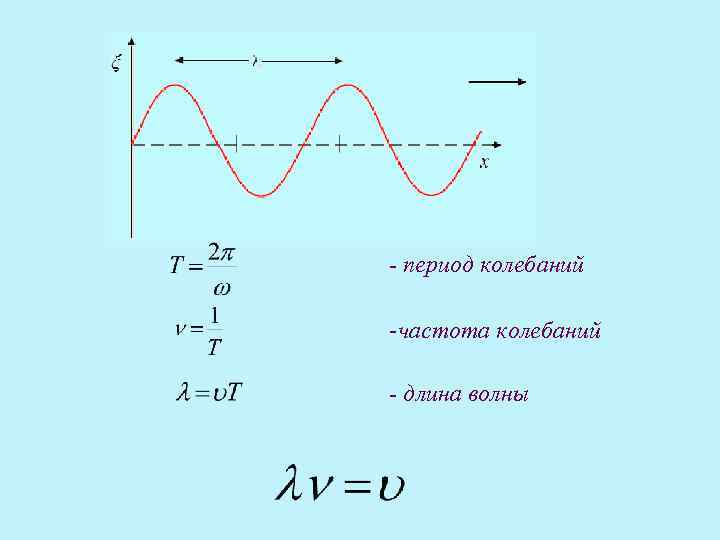- период колебаний -частота колебаний - длина волны

волновое число уравнение принимает вид Уравнение плоской волны, распространяющейся вдоль оси x

волновой вектор ( - нормаль к волновой поверхности) Уравнение плоской волны, распространяющейся в произвольном направлении

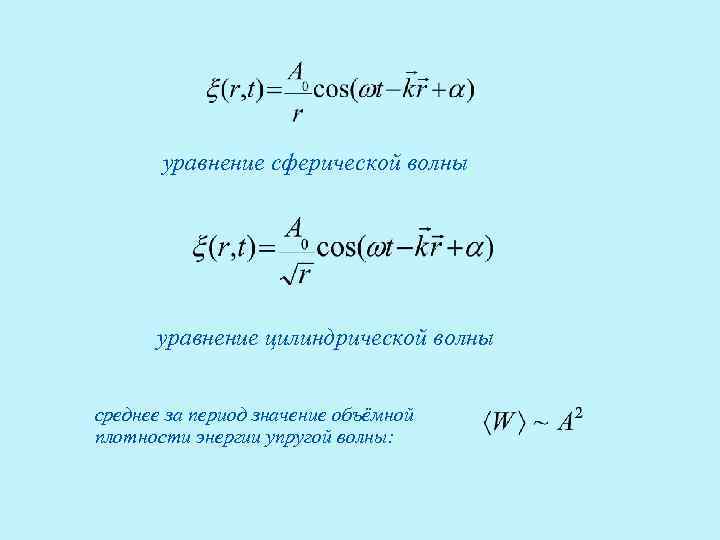уравнение сферической волны уравнение цилиндрической волны среднее за период значение объёмной плотности энергии упругой волны:

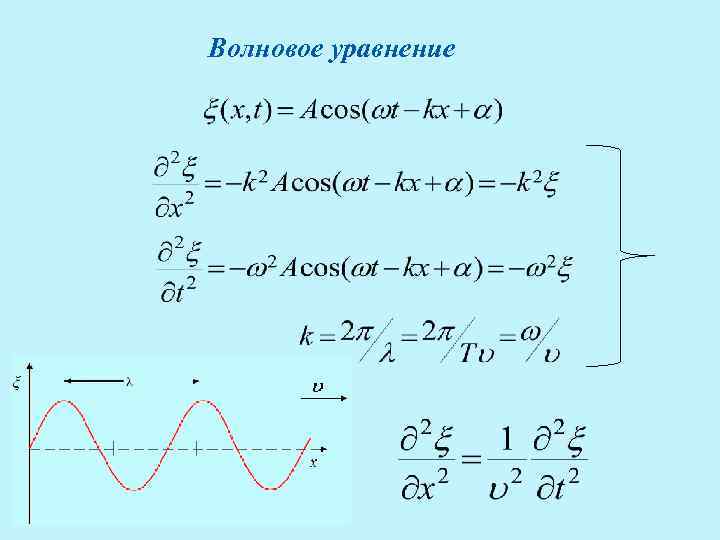Волновое уравнение

Для плоской волны, распространяющейся в произвольном направлении: где Δ – оператор Лапласа Волновое уравнение : Это уравнение справедливо для любой волны, в том числе и для плоской, сферической и цилиндрической

Электромагнитные волны Переменное электромагнитное поле Michael Faraday 1791 -1867 James Clerk Maxwell 1831 - 1879

В случае однородной электронейтральной (ρ=0) непроводящей (j=0) среды уравнения Максвелла принимают вид: по определению где - оператор Гамильтона

продифференцировав ур-я Максвелла получаем: или где

- скорость света в вакууме (µ=ε=1) В веществе скорость распространения электромагнитных волн меньше в n раз - фазовая скорость электромагнитной волны - абсолютный показатель преломления среды

Из уравнений Максвелла также получаем: В электромагнитной волне переменное во времени электрическое поле порождает направленное перпендикулярно ему переменное магнитное поле и наоборот, то есть поля E и H перпендикулярны другу

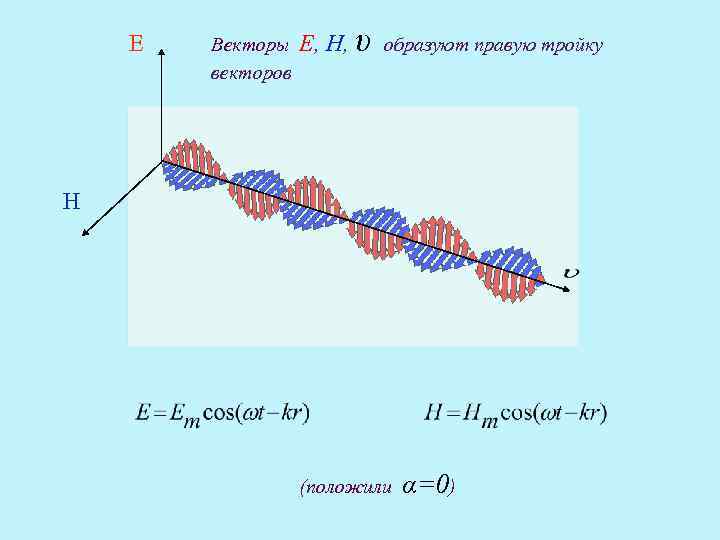E Векторы векторов E, H, υ образуют правую тройку H (положили α=0)

Физиологическое, фотохимическое, фотоэлектрическое и другие действия света обусловлены колебаниями электрического вектора Е. Принято говорить о световом векторе, имея в виду вектор Е.

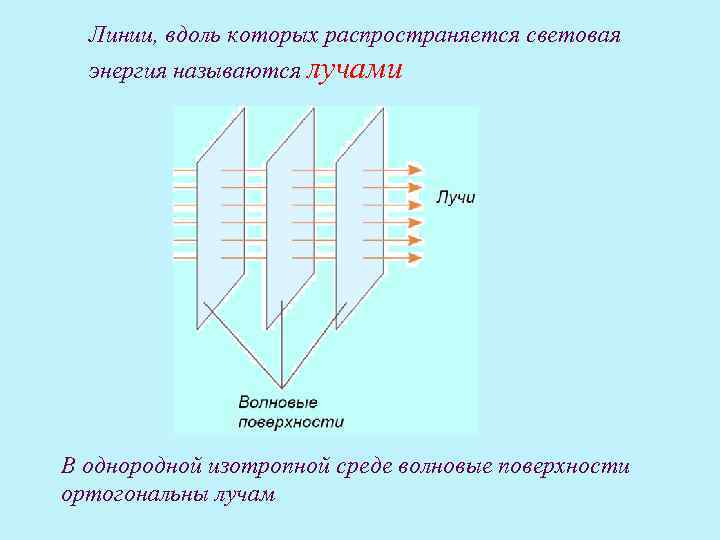Линии, вдоль которых распространяется световая энергия называются лучами В однородной изотропной среде волновые поверхности ортогональны лучам

Световая волна на границе раздела сред абсолютный показатель преломления среды относительный показатель преломления Когда свет проходит через границу раздела фаз его частота не меняется, а длина волны уменьшается

Плоская световая волна падает нормально на границу раздела диэлектриков с показателями преломления п 1 и п 2 на границе раздела сред тангенциальные составляющие и непрерывны: Можно показать, что векторы и связаны соотношением где ( - орт вдоль направления распространения волны образуют правую тройку векторов)

Решая совместно (1) м (2) получаем: - Колебания падающей и прошедшей волны происходит в одной фазе, при прохождении через границу фаза не претерпевает скачка; -Колебания падающей и прошедшей волны происходят в одной фазе, если n 2n 1, направление Е и Еʹ противоположны. При отражении от оптически более плотной среды фаза волны изменяется скачком на π.

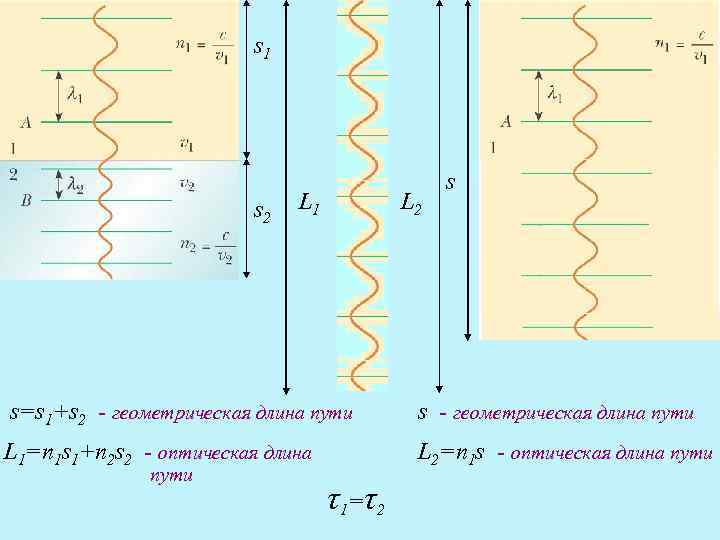s 1 s 2 L 1 L 2 s s=s 1+s 2 - геометрическая длина пути s - геометрическая длина пути L 1=n 1 s 1+n 2 s 2 - оптическая длина L 2=n 1 s - оптическая длина пути τ1=τ2

В вакууме (п=1) оптическая длина пути равна геометрической длине пути - оптическая длина пути Оптическая длина пути равна расстоянию, которое свет пройдет за то же время в вакууме Свет распространяется по такому пути, оптическая длина которого минимальна

В 1888 г. Герц экспериментально доказал существование электромагнитных волн, распространяющихся в свободном пространстве, предсказанных теорией Максвелла. Генрих Рудольф Герц (1857 – 1894) Экспериментируя с электромагнитными волнами, Герц наблюдал их отражение, преломление, интерференцию, поляризацию. Установил, что электромагнитная волна является поперечной, а скорость распространения электромагнитных волн равна скорости света.

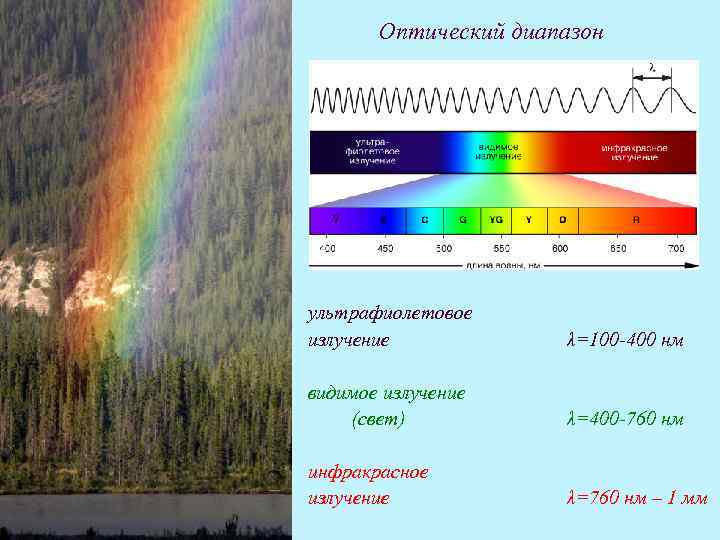Оптический диапазон ультрафиолетовое излучение λ=100 -400 нм видимое излучение (свет) λ=400 -760 нм инфракрасное излучение λ=760 нм – 1 мм