Short Version 20 Electric Charge Force

Short Version : 20. Electric Charge, Force, & Fields

20. 1. Electric Charge 2 kinds of charges: + & . Total charge = algebraic sum of all charges. Like charges repel. Opposite charges attract. = elementary charge All electrons have charge e. All protons have charge +e. 1 st measured by Millikan on oil drops. Theory (standard model) : basic unit of charge (carried by quark) = 1/3 e. Quark confinement no free quark can be observed. Smallest observable charge is e. Conservation of charge: total charge in a closed region is always the same.

Coulomb’s law (force between 2 point charges) : [q] = Coulomb = C

Conceptual Example 20. 1. Gravity & Electric Force The electric force is far stronger than the gravitational force, yet gravity is much more obvious in everyday life. Why? Only 1 kind of gravitational “charge” forces from different parts of a source tend to reinforce. 2 kinds of electric charges forces from different parts of a neutral source tend to cancel out.

Making the Connection Compare the magnitudes of the electric & gravitational forces between an electron & a proton.

Point Charges & the Superposition Principle Extension of Coulomb’s law (point charges) to charge distributions. Superposition principle: Fnet F 23 F 13 Task: Find net force on q 3. Independent of each other

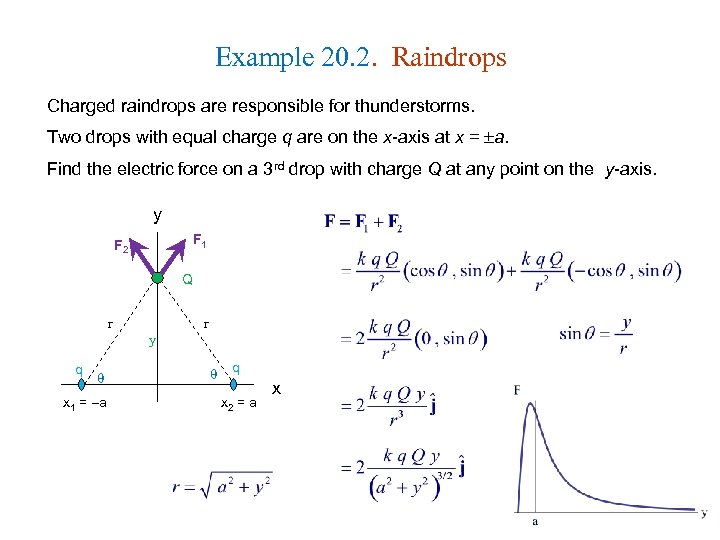Example 20. 2. Raindrops Charged raindrops are responsible for thunderstorms. Two drops with equal charge q are on the x-axis at x = a. Find the electric force on a 3 rd drop with charge Q at any point on the y-axis. y F 1 F 2 Q r q x 1 = a y r q x 2 = a x

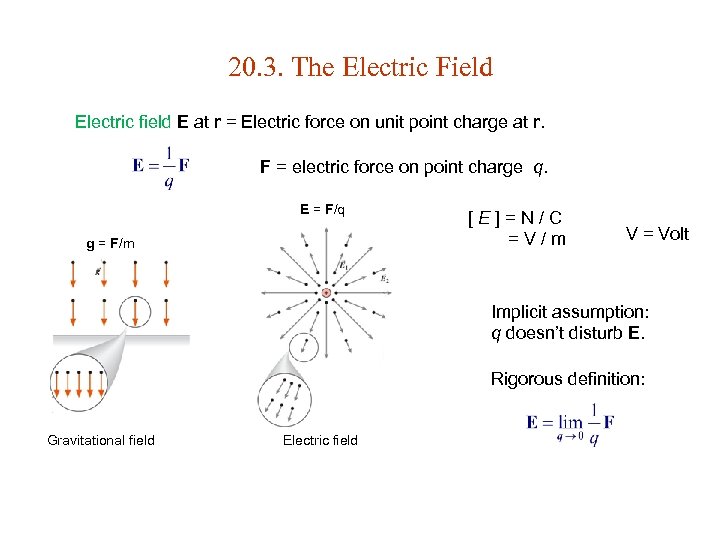20. 3. The Electric Field Electric field E at r = Electric force on unit point charge at r. F = electric force on point charge q. E = F/q g = F/m [E]=N/C =V/m V = Volt Implicit assumption: q doesn’t disturb E. Rigorous definition: Gravitational field Electric field

Force approach: Charges interact at a distance (difficult to manage when many charges are present). Fails when charge distributions are not known. Field approach: Charge interacts only with field at its position. No need to know how field is generated. Given E:

The Field of a Point Charge Field at r from point charge q : Field vectors for a negative point charge.

20. 4. Fields of Charge Distributions Superposition principle (Discrete sources) (Point charges)

The Electric Dipole Electric dipole = Two point charges of equal magnitude but opposite charges separated by a small distance. . Examples: Polar molecules. Heart muscle during contraction Electrocardiograph (EKG) Radio & TV antennas. H 2 O

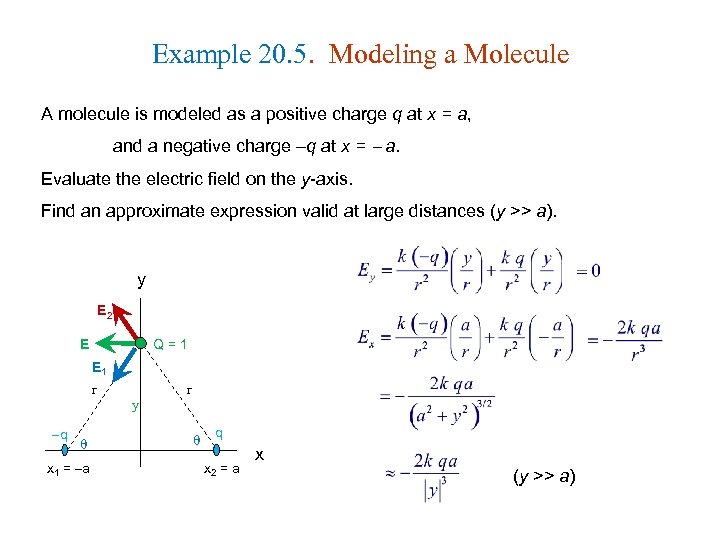Example 20. 5. Modeling a Molecule A molecule is modeled as a positive charge q at x = a, and a negative charge q at x = a. Evaluate the electric field on the y-axis. Find an approximate expression valid at large distances (y >> a). y E 2 E Q=1 E 1 r q x 1 = a y r q x 2 = a x (y >> a)

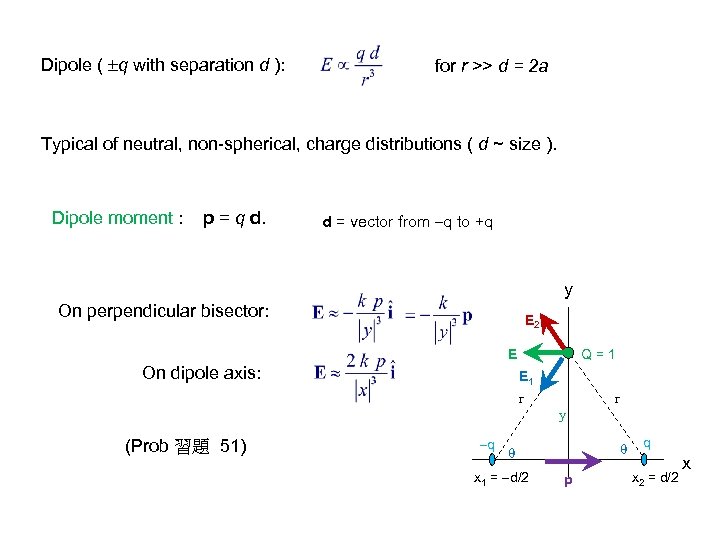Dipole ( q with separation d ): for r >> d = 2 a Typical of neutral, non-spherical, charge distributions ( d ~ size ). Dipole moment : p = q d. d = vector from q to +q y On perpendicular bisector: E 2 E On dipole axis: Q=1 E 1 r (Prob 習題 51) q y x 1 = d/2 r p q x 2 = d/2 x

Continuous Charge Distributions All charge distributions are ultimately discrete ( mostly protons & electrons ). Continuum approximation: Good for macroscopic bodies. Volume charge density [ C/m 3 ] Surface charge density [ C/m 2 ] Line charge density [ C/m ]

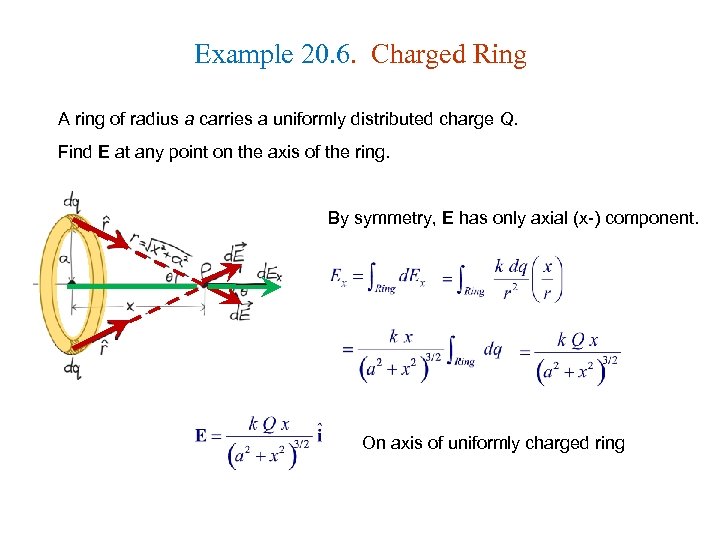Example 20. 6. Charged Ring A ring of radius a carries a uniformly distributed charge Q. Find E at any point on the axis of the ring. By symmetry, E has only axial (x-) component. On axis of uniformly charged ring

Example 20. 7. Power Line A long electric power line running along the x-axis carries a uniform charge density [C/m]. Find E on the y-axis, assuming the wire to be infinitely long. d. Ey y By symmetry, E has only y- component. d. E P r dq r y x dq x Perpendicular to an infinite wire

20. 5. Matter in Electric Fields Point Charges in Electric Fields Newton’s 2 nd law (point charge in field E) Trajectory determined by charge-to-mass ratio q/m. Constant E constant a. E. g. , CRT, inkjet printer, …. Uniform field between charged plates (capacitors).

Example 20. 8. Electrostatic Analyzer Two curved metal plates establish a field of strength E = E 0 ( b/r ), where E 0 & b are constants. E points toward the center of curvature, & r is the distance to the center. Find speed v with which a proton entering vertically from below will leave the device moving horizontally. Too fast, hits outer wall For a uniform circular motion: Too slow, hits inner wall

Dipoles in Electric Fields Uniform E: Total force: Torque about center of dipole: = dipole moment Work done by E to rotate dipole : Potential energy of dipole in E ( i = /2) t // tangent ( U = 0 for p E )

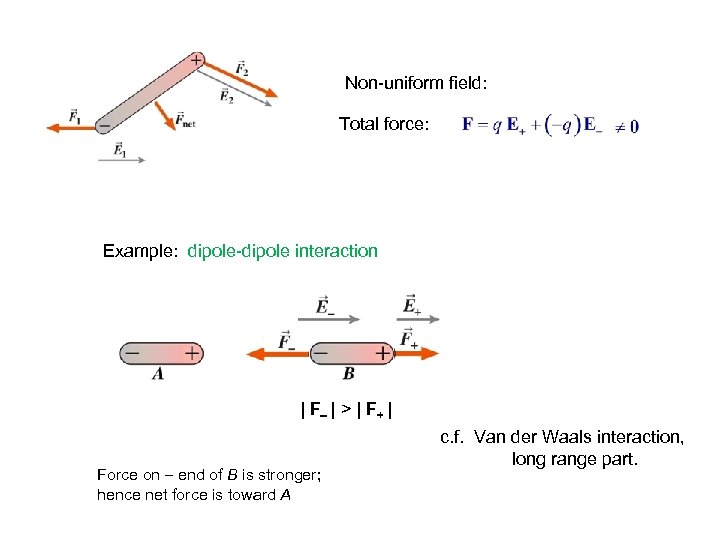Non-uniform field: Total force: Example: dipole-dipole interaction | F | > | F+ | Force on end of B is stronger; hence net force is toward A c. f. Van der Waals interaction, long range part.

Application: Microwave Cooking & Liquid Crystals Microwave oven: GHz EM field vibrates (dipolar) H 2 O molecules in food heats up. Liquid Crystal Display (LCD) dipolar molecules aligned but positions irregular

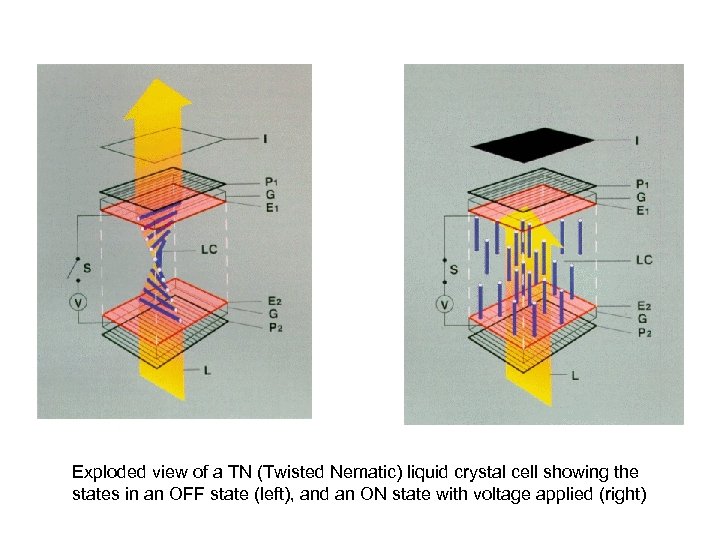Exploded view of a TN (Twisted Nematic) liquid crystal cell showing the states in an OFF state (left), and an ON state with voltage applied (right)

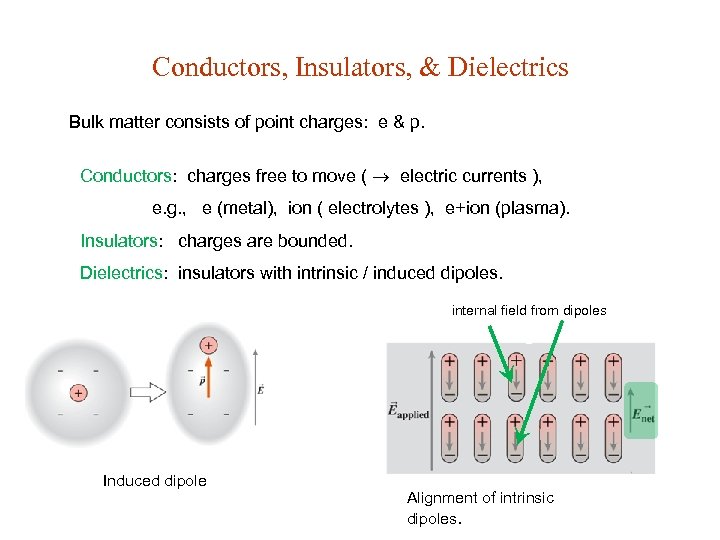Conductors, Insulators, & Dielectrics Bulk matter consists of point charges: e & p. Conductors: charges free to move ( electric currents ), e. g. , e (metal), ion ( electrolytes ), e+ion (plasma). Insulators: charges are bounded. Dielectrics: insulators with intrinsic / induced dipoles. internal field from dipoles Induced dipole Alignment of intrinsic dipoles.