Школа соционики в Москве О взаимодействии и упорядочении

Школа соционики в Москве О взаимодействии и упорядочении признаков Рейнина Осипов А. В.

Диагностика Основы диагностики: 1. 2. 3. 4. базис Юнга (4) модель А признаки Рейнина (11) малые группы (квадры, клубы, темпераменты, и т. п. ) 5. интертипные отношения 6. … на практике: - трудноопределимы затруднено определяются легко и с высокой степенью достоверности Как поступить в такой ситуации? Как эффективнее использовать знание признаков Рейнина и их свойств?

План доклада 1. признаки Рейнина 2. порядок (нумерация) признаков и таблицы умножения 3. примеры практического применения таблиц

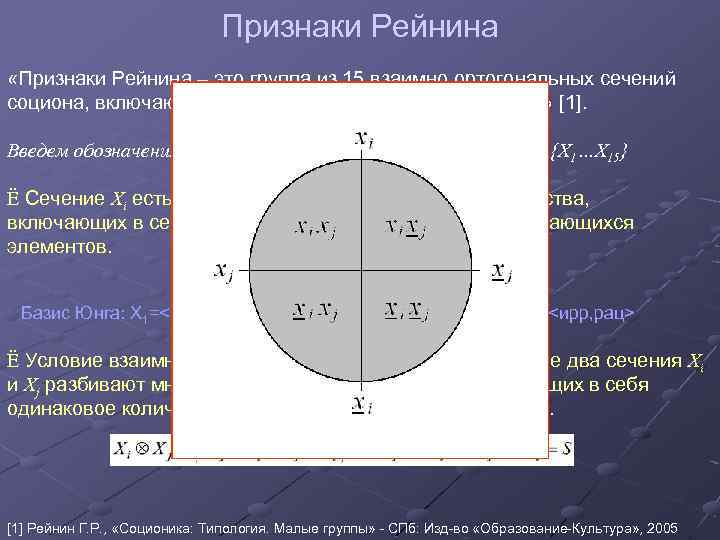Признаки Рейнина «Признаки Рейнина – это группа из 15 взаимно ортогональных сечений социона, включающая в себя 4 базовых дихотомии Юнга» [1]. Введем обозначения: социон S={T 1…T 16}, признаки Рейнина Q={X 1…X 15} Ё Сечение Хi есть разбиение множества S на 2 подмножества, включающих в себя одинаковое количество (8) непересекающихся элементов. Базис Юнга: Х 1=<экстр, интр>, Х 2=<лог, эт>, Х 3=<инт, сенс>, Х 4=<ирр, рац> Ё Условие взаимной ортогональности означает, что любые два сечения Xi и Xj разбивают множество S на 4 подмножества, включающих в себя одинаковое количество (4) непересекающихся элементов. [1] Рейнин Г. Р. , «Соционика: Типология. Малые группы» - СПб: Изд-во «Образование-Культура» , 2005

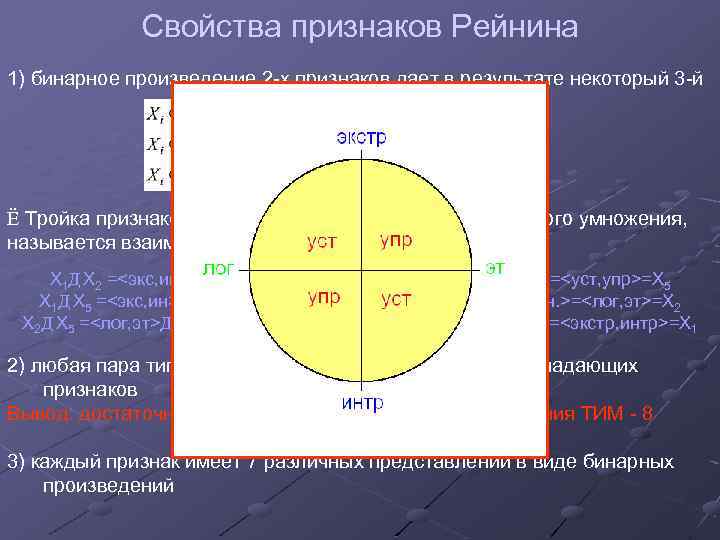Свойства признаков Рейнина 1) бинарное произведение 2 -х признаков дает в результате некоторый 3 -й Ё Тройка признаков Xi, Xj, Xk, связанных операцией бинарного умножения, называется взаимозависимой. Х 1 Д Х 2 =<экс, ин>Д<лог, эт>=<экс. лог. Иин. эт. , экс. эт. Иин. лог. >=<уст, упр>=Х 5 Х 1 Д Х 5 =<экс, ин>Д<уст, упр>=<уст. экс. Иупр. ин. , упр. экс. Иуст. ин. >=<лог, эт>=Х 2 Х 2 Д Х 5 =<лог, эт>Д<уст, упр>=<уст. лог. Иупр. эт. , упр. лог. Иуст. эт. >=<экстр, интр>=Х 1 2) любая пара типов ИМ имеет 7 совпадающих и 8 несовпадающих признаков Вывод: достаточное количество признаков для определения ТИМ - 8 3) каждый признак имеет 7 различных представлений в виде бинарных произведений

Таблица умножения и порядок признаков Рейнина Взаимосвязь всех 15 -и признаков Рейнина через операцию умножения удобно представить в виде таблицы. Расстановка элементов в таблице будет определяться порядком (нумерацией) признаков (можно сказать, что порядок признаков есть ключ к таблице умножения). 1. порядок, принятый в соответствии с базисом Юнга и введенными Рейниным правилами умножения В работах Рейнина представлена такая таблица, но отсутствует ключ к ней. 2. порядок, принятый в таблице признаков Рейнина Порядок, представленный в таблице признаков Рейнина, был выбран достаточно произвольно для удобства разбиения их на индивидуальные, диадные, квадровые. Поэтому вышеуказанные правила умножения, а следовательно, и таблица умножения для них нарушены. Т. о. , есть ключ, но нет таблицы.

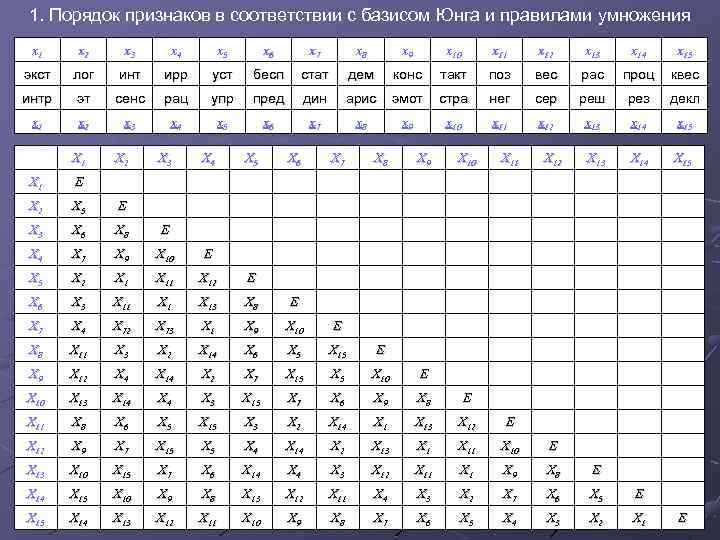1. Порядок признаков в соответствии с базисом Юнга и правилами умножения x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 экст лог инт ирр уст бесп стат дем конс такт поз вес рас проц квес интр эт сенс рац упр пред дин арис эмот стра нег сер реш рез декл x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 X 13 X 14 X 15 X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 11 X 12 X 1 Е X 2 X 5 Е X 3 X 6 X 8 Е X 4 X 7 X 9 X 10 Е X 5 X 2 X 11 X 12 Е X 6 X 3 X 11 X 13 X 8 Е X 7 X 4 X 72 X 73 X 1 X 9 X 10 Е X 8 X 11 X 3 X 2 X 14 X 6 X 5 X 15 Е X 9 X 12 X 4 X 14 X 2 X 7 X 15 X 10 Е X 10 X 13 X 14 X 3 X 15 X 7 X 6 X 9 X 8 Е X 11 X 8 X 6 X 5 X 15 X 3 X 2 X 14 X 13 X 12 Е X 12 X 9 X 7 X 15 X 4 X 14 X 2 X 13 X 11 X 10 Е X 13 X 10 X 15 X 7 X 6 X 14 X 3 X 12 X 11 X 9 X 8 Е X 14 X 15 X 10 X 9 X 8 X 13 X 12 X 11 X 4 X 3 X 2 X 7 X 6 X 5 Е X 15 X 14 X 13 X 12 X 11 X 10 X 9 X 8 X 7 X 6 X 5 X 4 X 3 X 2 X 1 Е

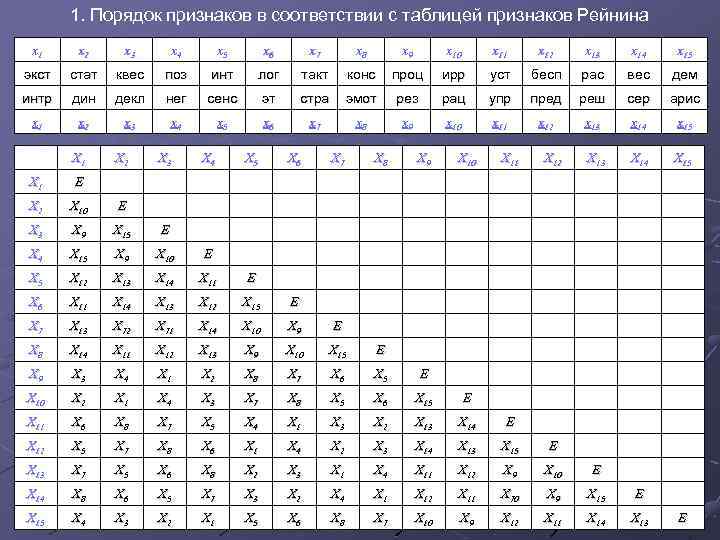1. Порядок признаков в соответствии с таблицей признаков Рейнина x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 экст стат квес поз инт лог такт конс проц ирр уст бесп рас вес дем интр дин декл нег сенс эт стра эмот рез рац упр пред реш сер арис x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 X 13 X 14 X 15 X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 11 X 12 X 1 Е X 2 X 10 Е X 3 X 9 X 15 Е X 4 X 15 X 9 X 10 Е X 5 X 12 X 13 X 14 X 11 Е X 6 X 11 X 14 X 13 X 12 X 15 Е X 7 X 13 X 72 X 71 X 14 X 10 X 9 Е X 8 X 14 X 11 X 12 X 13 X 9 X 10 X 15 Е X 9 X 3 X 4 X 1 X 2 X 8 X 7 X 6 X 5 Е X 10 X 2 X 1 X 4 X 3 X 7 X 8 X 5 X 6 X 15 Е X 11 X 6 X 8 X 7 X 5 X 4 X 1 X 3 X 2 X 13 X 14 Е X 12 X 5 X 7 X 8 X 6 X 1 X 4 X 2 X 3 X 14 X 13 X 15 Е X 13 X 7 X 5 X 6 X 8 X 2 X 3 X 1 X 4 X 11 X 12 X 9 X 10 Е X 14 X 8 X 6 X 5 X 7 X 3 X 2 X 4 X 12 X 11 X 70 X 9 X 15 Е X 15 X 4 X 3 X 2 X 1 X 5 X 6 X 8 X 7 X 10 X 9 X 12 X 11 X 14 X 13 Е

Примеры практического применения 1. Проверка истинности определения 2 -х признаков 3 -м. диагностика Xi Xj определение Xk, являющегося взаимозависимым к Xi, Xj диагностика проверка Xk как провериться? - если “=“, то признаки Xi, Xj определены верно (либо оба – неверно) - если “№ то один из признаков Xi, Xj определен неверно “, 2. Определение труднодиагностируемого признака через другие (опосредованно). диагностика Xi как определить? определение Xj, Xk, являющихся взаимозависимыми к Xi диагностика Xj Xk

3. Проверка достаточности 4 -ки признаков для определения ТИМ. Любая 4 -ка взаимонезависимых признаков составляет базис для определения ТИМ. Для 15 признаков существует 840 равноправных базисов (включая традиционный базис Юнга) [1]. диагностика Xi Xj Xk проверка признаков на взаимозависимость (по таблице бинарных произведений) Xl Xi, Xj, Xk достаточно ли их для определения ТИМ? Xi, Xk, Xl Xj, Xk, Xl - если каждая тройка взаимо. НЕзависима, то данных 4 -х признаков достаточно для определения ТИМ - если хотя бы одна из троек является взаимозависимой, то данных 4 -х признаков недостаточно для определения ТИМ Пример диагностика экст лог инт ирр ИЛЭ диагностика ИЛЭ СЛЭ экст лог уст ирр [1] Рейнин Г. Р. , «Соционика: Типология. Малые группы» - СПб: Изд-во «Образование-Культура» , 2005