Шифрование с открытым ключом Криптосистема RSA Докладчик Евгений

Шифрование с открытым ключом: Криптосистема RSA Докладчик: Евгений Сеппель (344 гр. 5/6 у. г. ) Математико-механический факультет СПб. ГУ

О системе Создана в 1977 г. Ronald Rivest, Adi Shamir и Leonard Adleman. Использует принцип открытого ключа 2

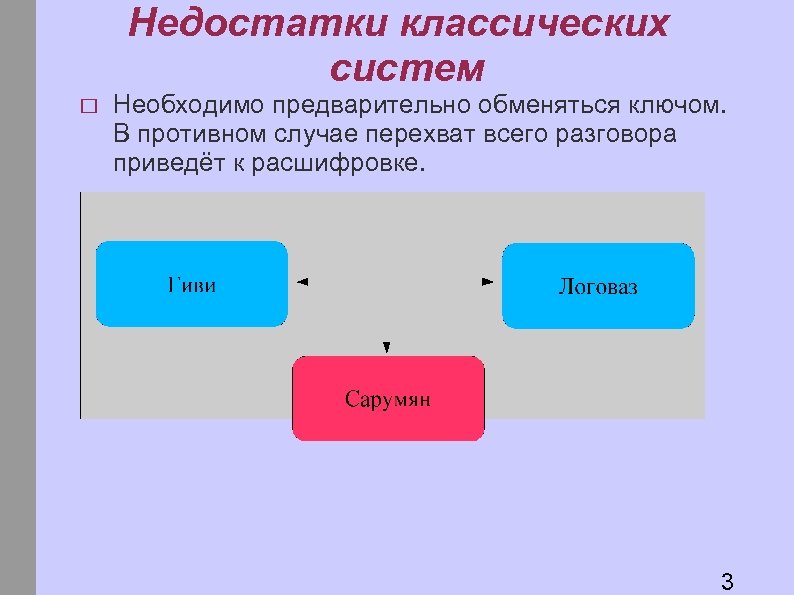Недостатки классических систем Необходимо предварительно обменяться ключом. В противном случае перехват всего разговора приведёт к расшифровке. 3

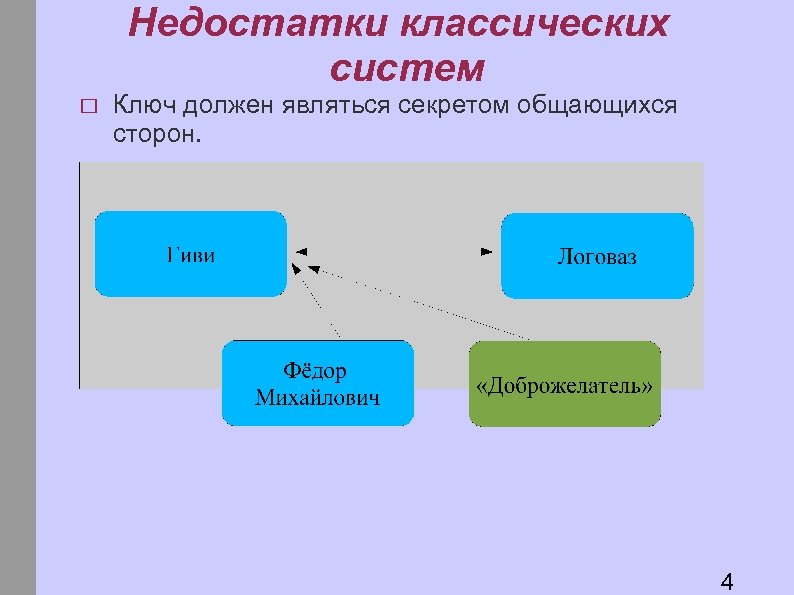Недостатки классических систем Ключ должен являться секретом общающихся сторон. 4

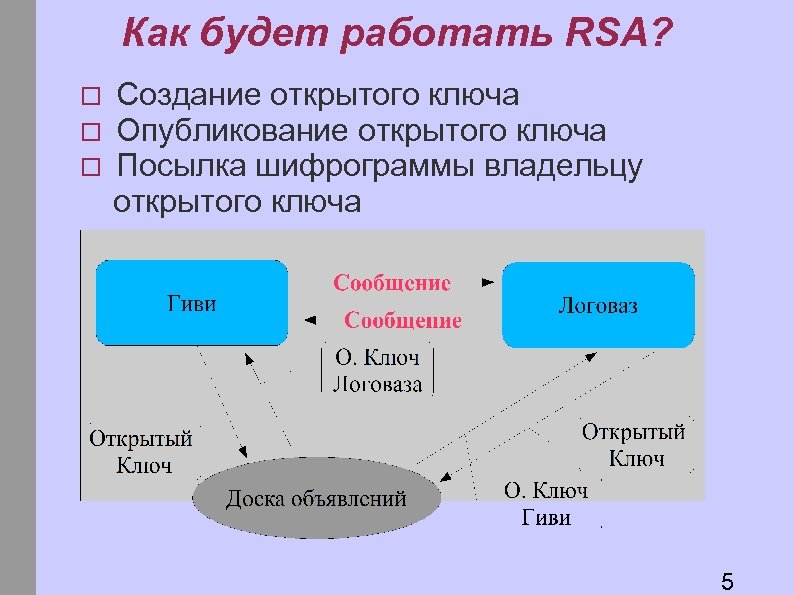Как будет работать RSA? Создание открытого ключа Опубликование открытого ключа Посылка шифрограммы владельцу открытого ключа 5

Поподробнее. . Пусть PГ PЛ – открытые ключи, SГ SЛ – секретные ключи D – множество всех возможных сообщений. И SЛ(M), PЛ(M), где M D суть перестановки. (Каждая из них может быть быстро вычислена если известен P или S) Необходима взаимная обратность перестановок одного владельца: SЛ(PЛ(M)) = M PЛ(SЛ(M)) = M M D Никто кроме владельца не должен уметь находить S() за разумное время!!! 6

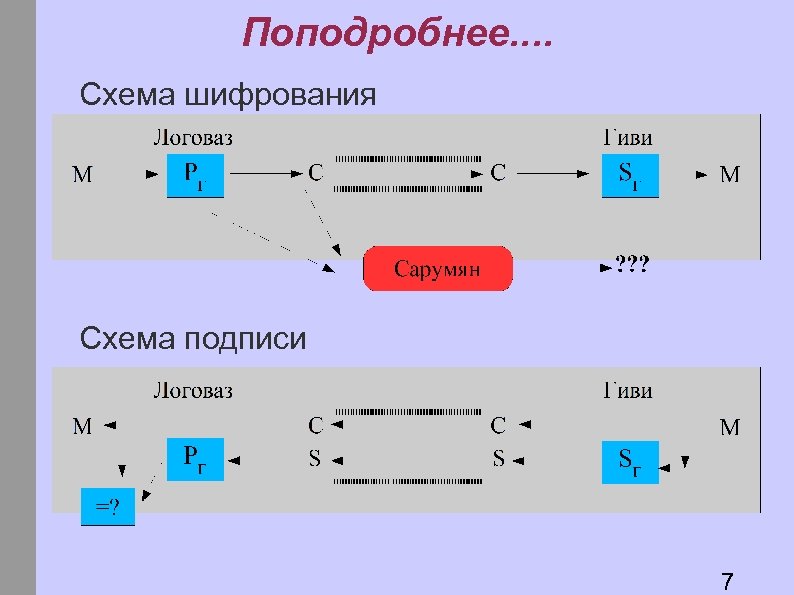Поподробнее. . Схема шифрования Схема подписи 7

RSA Берём 2 больших простых числа p, q (~100 знаков) n: =p*q произведение простых чисел Пусть (n) – функция Эйлера (Число элементов в Zn) (n) = (p-1)(q-1) Возьмём небольшое e взаимно простое с (n) Найдём d=e-1 mod (n) (оно и однозначно по mod) Теперь P = (e, n) S = (d, n) D=Zn e P(M) = M mod n d S(C) = C mod n 8

Время Заметим, что если числа d, n имеют порядка бит , число e имеет O(1) бит, то преобразование P потребует O(1) умножений по модулю n (O( 2) битовых операций), а преобразование S – O( ) умножений (O( 3) битовых операций). Мы пользуемся методом повторного возведения в квадрат. Теорема P() S() задают взаимно обратные перестановки D. P(S(M)) = S(P(M)) = Med mod n. e и d взаимно обратны по mod (n) => ed = 1+k(p-1)(q-1) для некоторого k По малой теореме Ферма Med M(Mp-1)k(q-1) M*1 k(q-1) M 9

Надёжность Трудно разложить n на p и q! Если легко разложить=> легко взломать Если трудно разложить =? > трудно взломать Задача восстановления секретного ключа эквивалентна задаче разложения на множители модуля: можно использовать d для поиска сомножителей n, и наоборот, можно использовать n для поиска d. 10

Взлом Можно(? ) найти метод вычисления корня степени e из mod n. С = Me mod n, => корнень степени e из mod n = M. Но мы так ещё не умеем. . ☻ Если на основе одного и того же e относительно небольшой величины шифруется много связанных сообщений, есть возможность вскрыть сообщения. Упомянутые атаки — единственные способы расшифровать все сообщения, зашифрованные данным ключом RSA. восстановление исходной информации по ее криптограмме; вычисление закрытого ключа по известному открытому; формирование электронной цифровой подписи сообщения без знания закрытого ключа; создание фальшивого электронного документа, соответствующего известной подписи. 11

Взлом Успехи: В конце 95 года удалось практически реализовать раскрытие шифра RSA для 500 -значного ключа. Для этого с помощью Интеpнета было задействовано 1600 компьютеров. (три-пять лет -- практическое время взлома) рекомендации по длине ключа n: - 768 бит — для частных лиц; - 1024 бит — для коммерческой информации; - 2048 бит — для особо секретной информации 12

Список Литературы Т. Кормен. «Алгоритмы: Построение и анализ» -- М. МЦНМО, 2002 Б. Шнайер. «Прикладная Криптография» 2 -е издание S. Goldwasser. «Lecture notes on Cryptography» 2001 Э. А. Гирш. Конспект лекций 3 -го семестра 2 курса потока матообеспечения. Мат-мех. 2004.