ШАР Вычисление площади поверхности и объема шара

ШАР. Вычисление площади поверхности и объема шара.

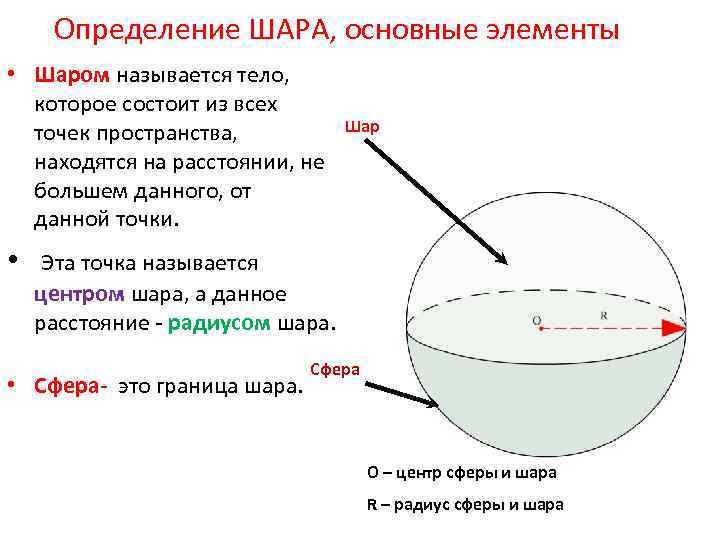
Определение ШАРА, основные элементы • Шаром называется тело, которое состоит из всех точек пространства, находятся на расстоянии, не большем данного, от данной точки. • Шар Эта точка называется центром шара, а данное расстояние - радиусом шара. • Сфера- это граница шара. Сфера O – центр сферы и шара R – радиус сферы и шара

Шар и сфера Граница шара называется шаровой поверхностью или сферой. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Касательная плоскость имеет с шаром только одну общую точку – точку касания.

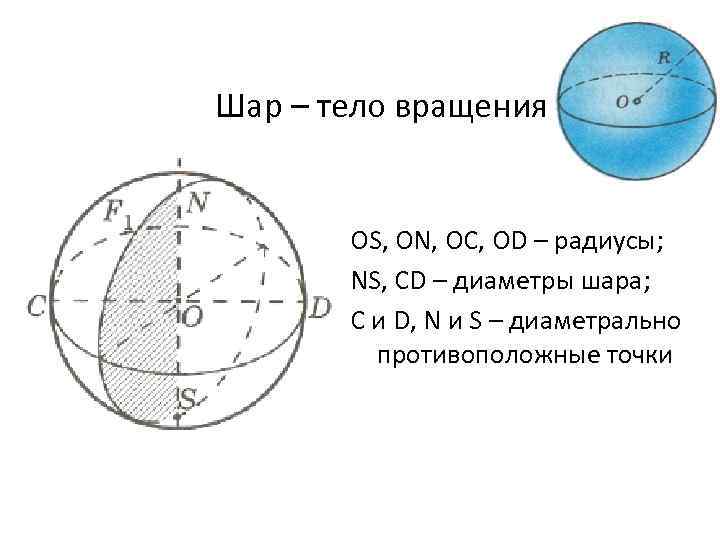
Шар – тело вращения OS, ON, OC, OD – радиусы; NS, CD – диаметры шара; C и D, N и S – диаметрально противоположные точки

• Точка О называется центром сферы, • R-радиус сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы, называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. • Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы. Теорема: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. . .

Площадь сферы Для определения площади сферы воспользуемся понятием описанного многогранника. Многогранник называется описанным около сферы (шара) , если сфера касается всех его граней. При этом сфера называется вписанной в многогранник. S=4 ПR 2

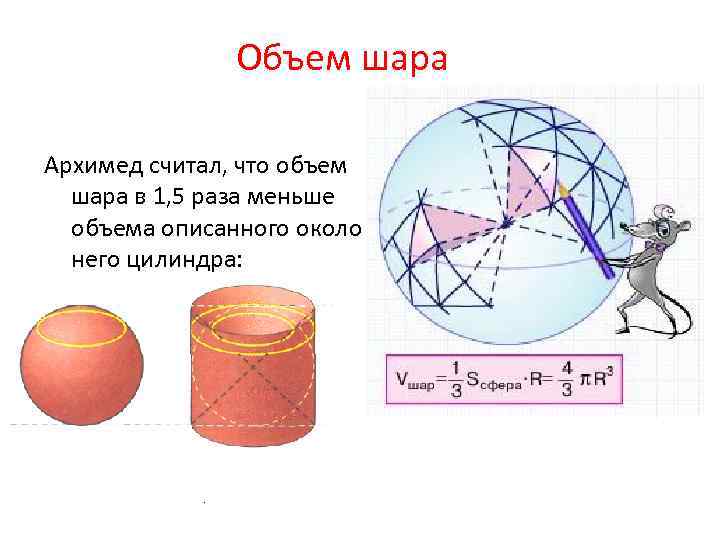
Объем шара Архимед считал, что объем шара в 1, 5 раза меньше объема описанного около него цилиндра: Vш=4/3πR³.

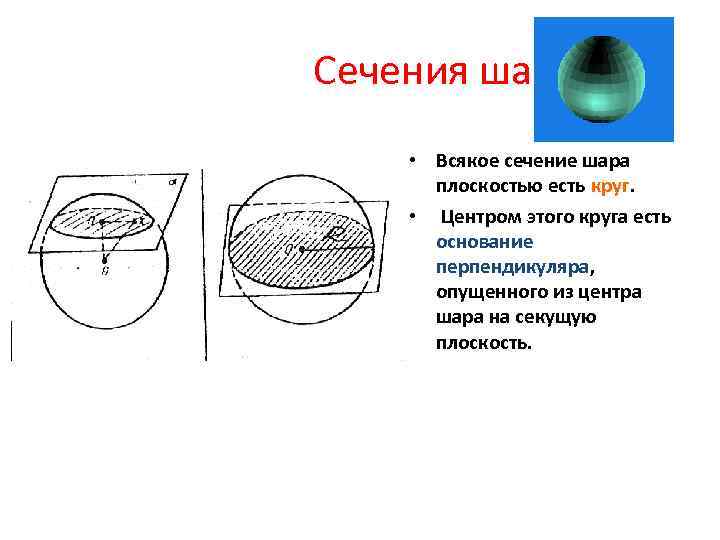
Сечения шара. • Всякое сечение шара плоскостью есть круг. • Центром этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

1. Шаровой сегмент • Шаровым сегментом называется часть шара, отсекаемая от него какойнибудь плоскостью. • Круг, получившийся в сечении, называется основанием каждого из этих сегментов. • Объём шарового сегмента

Элементы Шарового сегмента • Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью. • Основанием сегментов является круг, получившийся в сечении. • Высотами сегментов являются длины отрезков диаметра, перпендикулярного к секущей плоскости, где АС – диаметр, АВ и ВС – длины отрезков диаметра.

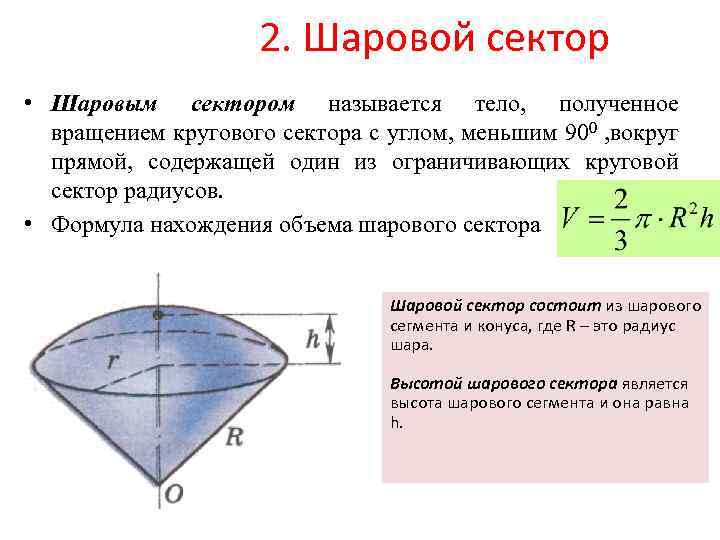
2. Шаровой сектор • Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 900 , вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов. • Формула нахождения объема шарового сектора Шаровой сектор состоит из шарового сегмента и конуса, где R – это радиус шара. Высотой шарового сектора является высота шарового сегмента и она равна h.

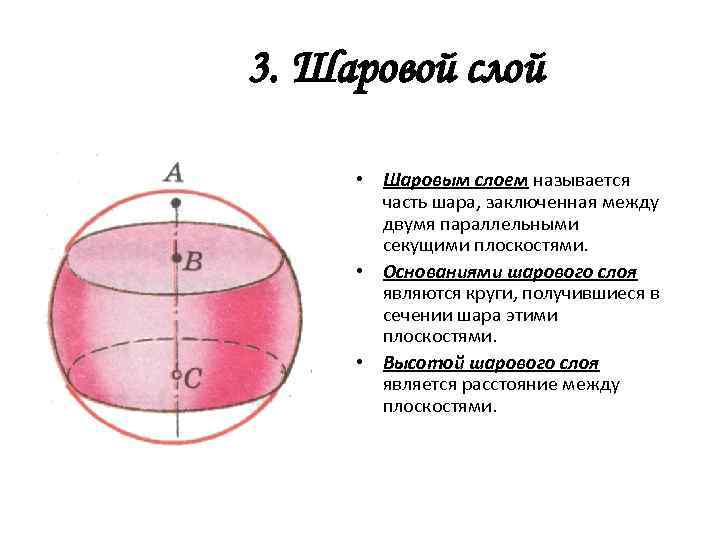
3. Шаровой слой • Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями. • Основаниями шарового слоя являются круги, получившиеся в сечении шара этими плоскостями. • Высотой шарового слоя является расстояние между плоскостями.

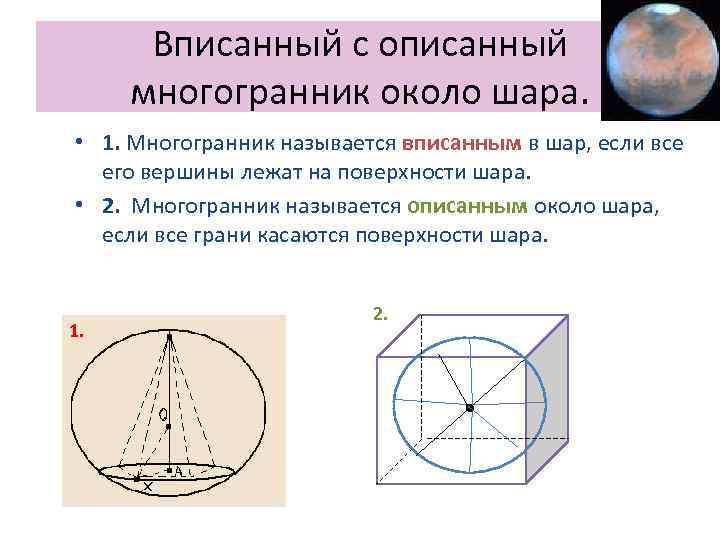
Вписанный с описанный многогранник около шара. • 1. Многогранник называется вписанным в шар, если все его вершины лежат на поверхности шара. • 2. Многогранник называется описанным около шара, если все грани касаются поверхности шара. 1. 2.