ШАР СФЕРА Работу выполнили студенты группы КТ-426 Шагавиев

ШАР. СФЕРА. Работу выполнили студенты группы КТ-426: Шагавиев Ильшат, Ларионова Оксана, Сугакова Дарья.

Исторические сведения Оба слова «шар» и «сфера» происходят от греческого слова «сфайра» - мяч. В древности сфера и шар были в большом почёте. Астрономические наблюдения над небесным сводом вызывали образ сферы. В XI книге «Начал» Евклид определяет шар как фигуру, описанную вращающимся около неподвижного диаметра полукругом Аристотель считал, что шарообразная форма, как наиболее совершенная, свойственна Солнцу, Земле, Луне и всем мировым телам. Так же он полагал, что Земля окружена рядом концентрических сфер. Сфера, шар всегда широко применялись в различных областях науки и техники.

Выдающиеся личности Евклид, древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Его главная работа "Начала" содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел.

Аристотель , древнегреческий философ. Аристотель был первым мыслителем, создавшим всестороннюю систему философии, охватившую все сферы человеческого развития: социологию, философию, политику, логику, физику.

Сказка про шар Однажды , оставшись один дома, красавец Полукруг долго принаряживался и жеманился перед небольшим в оловянных рамках зеркалом и не мог налюбоваться собою. «Что людям вздумалось расславлять , будто я хорош? - говорил он. – Лгут люди , я совсем не хорош. Почему девушки провозгласили , что лучшего парня и не было еще никогда и не будет никогда на селе Хатанга? » . Полукруг знал и слышал все, что про него говорили , и был капризным, как красавец. Он мог целый день любоваться собой перед зеркалом , рассматривая себя со всех сторон. И вдруг случилось чудо, когда Полукруг повернулся перед зеркалом вокруг себя, он увидел в зеркале собственное отражение в форме Шара

Определение Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки Сфера - шаровая поверхность – граница шара

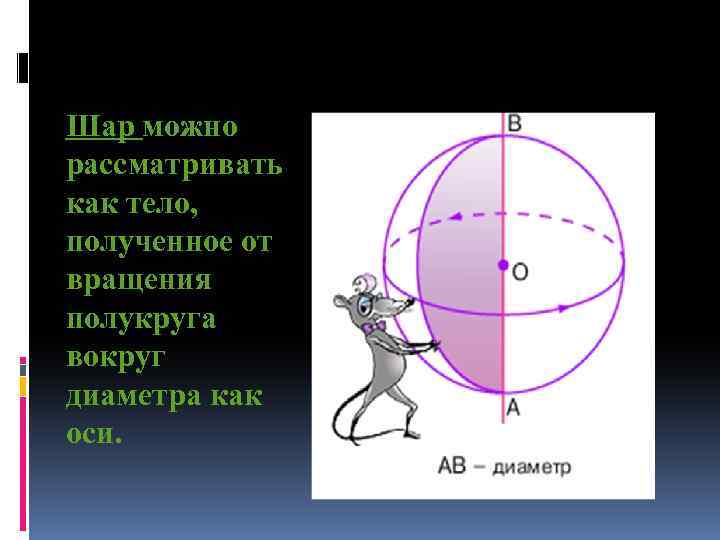
Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.

Элементы шара Центром называется точка пространства, которая расположена на заданном расстоянии.

Радиусом называется любой отрезок, соединяющий центр и какуюнибудь точку сферы

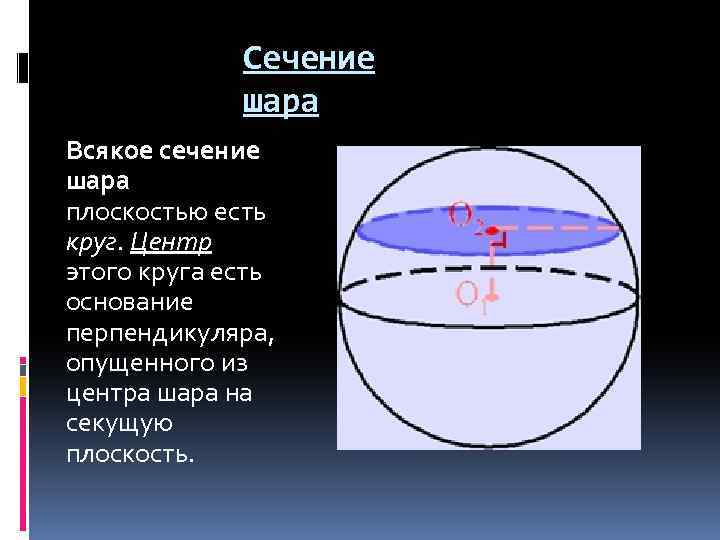
Сечение шара Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

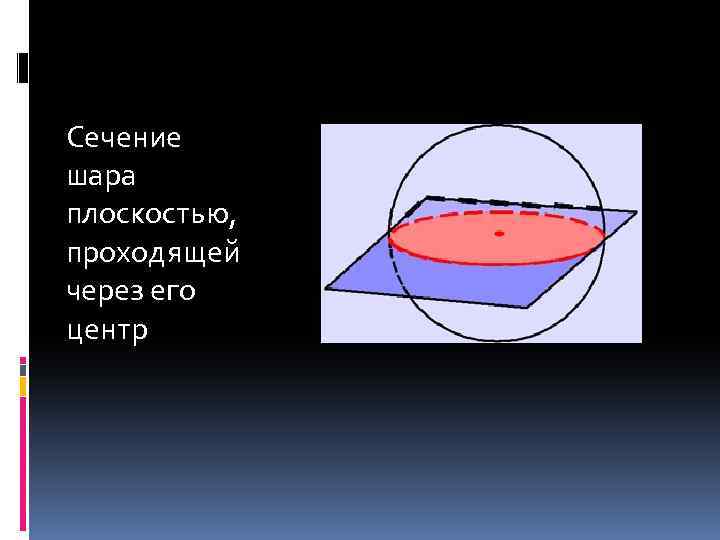
Сечение шара плоскостью, проходящей через его центр

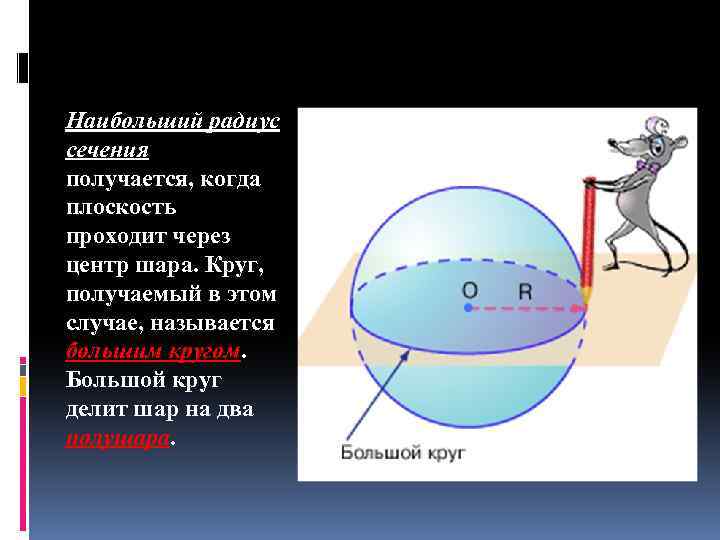
Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом. Большой круг делит шар на два полушара.

Плоскость и прямая, касательные к сфере Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью. Касательная плоскость перпендикулярна радиусу, проведенному в точку касания.

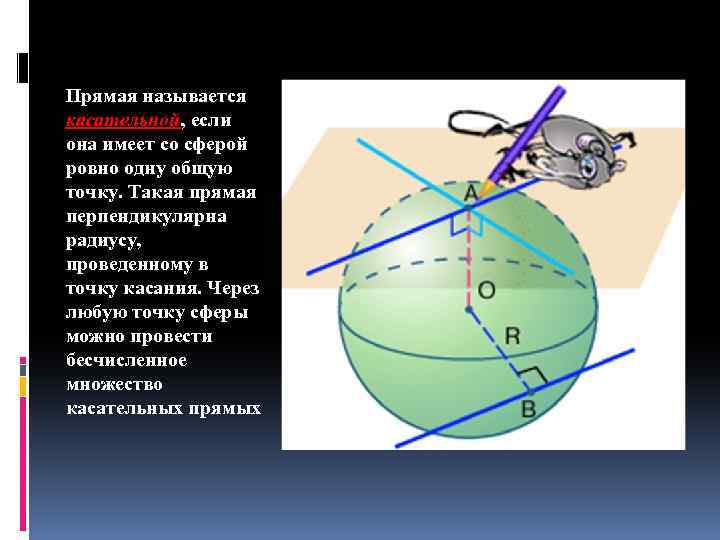
Прямая называется касательной, если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых

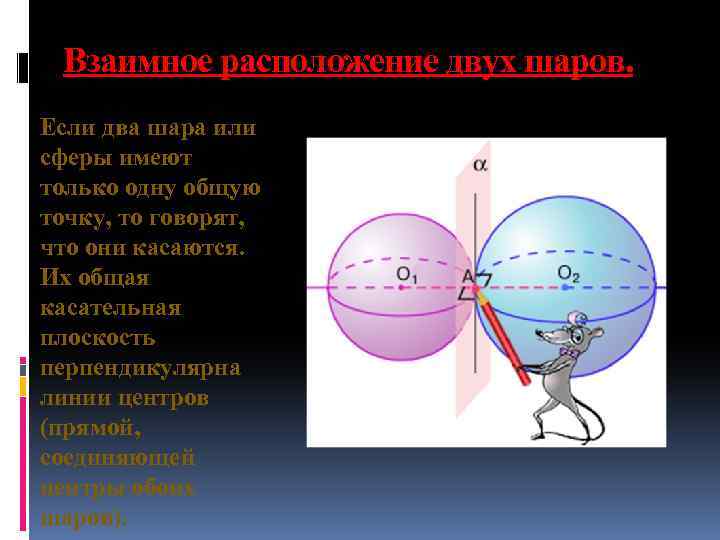
Взаимное расположение двух шаров. Если два шара или сферы имеют только одну общую точку, то говорят, что они касаются. Их общая касательная плоскость перпендикулярна линии центров (прямой, соединяющей центры обоих шаров).

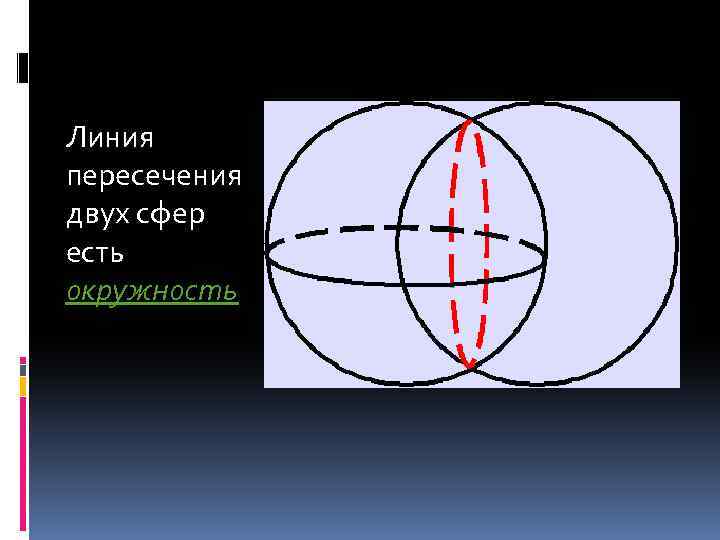
Линия пересечения двух сфер есть окружность

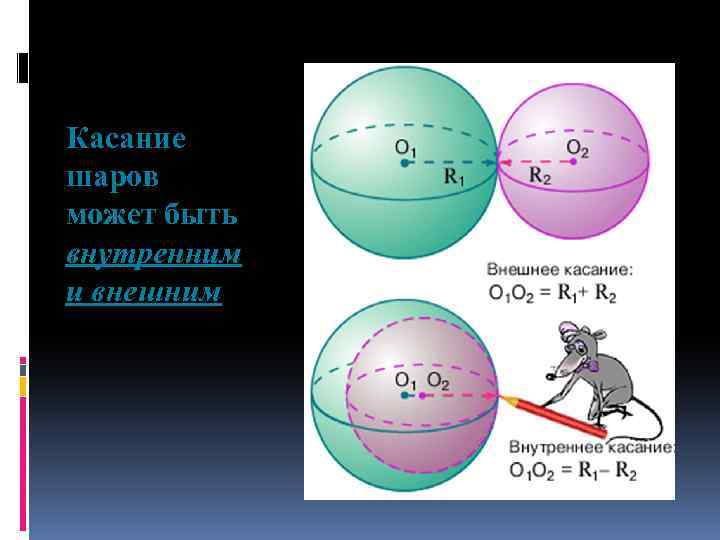
Касание шаров может быть внутренним и внешним

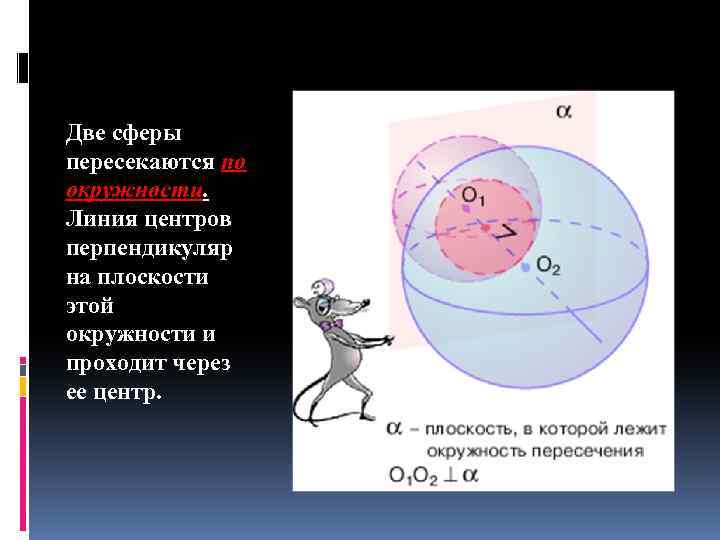
Две сферы пересекаются по окружности. Линия центров перпендикуляр на плоскости этой окружности и проходит через ее центр.

Вписанная и описанная сферы. Сфера (шар) называется описанной около многогранника, если все вершины многогранника лежат на сфере.

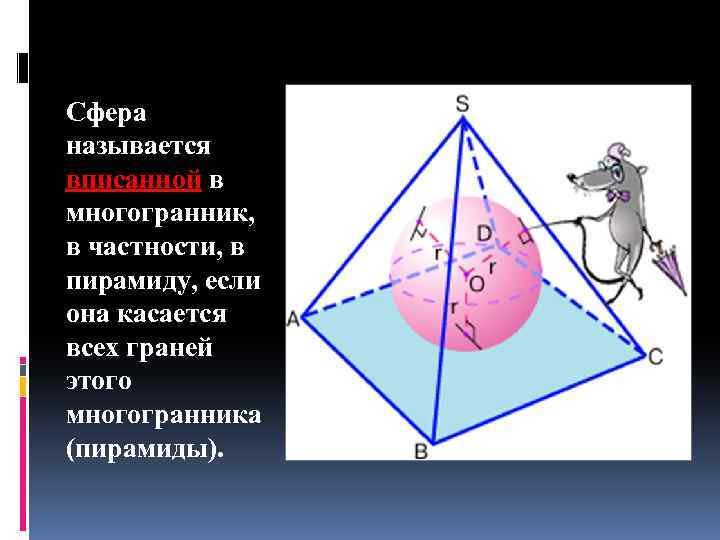
Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника (пирамиды).

Площадь сферы Для определения площади сферы воспользуемся понятием описанного многогранника. Многогранник называется описанным около сферы (шара) , если сфера касается всех его граней. При этом сфера называется вписанной в многогранник. Пусть описанный около сферы многогранник имеет n-граней. Будем неограниченно увеличивать n таким образом, чтобы наибольший размер каждой грани стремился к нулю. За площадь сферы примем предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани.

Формула площади сферы и шара

Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара

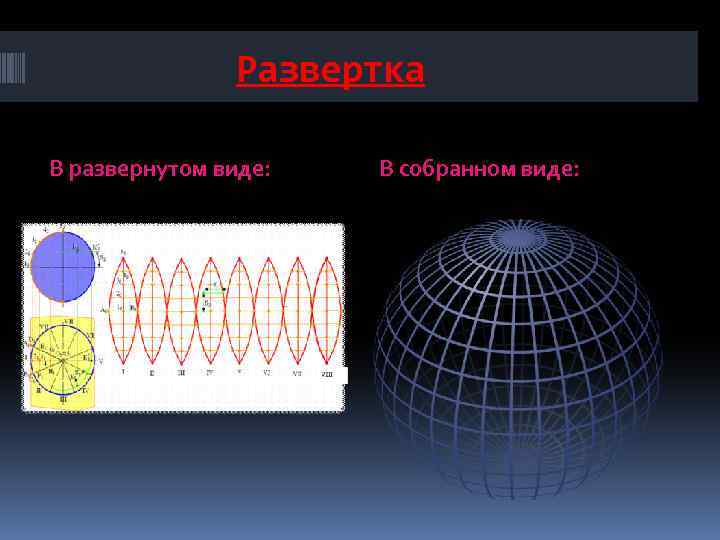
Развертка В развернутом виде: В собранном виде:

Задачи

Задача: Сечение шара плоскостью имеет площадь 36π(м 2). Радиус шара 10 м. Найти расстояние от центра шара до плоскости сечения. Дано: шар. S(O, OX) Sсеч= 36π(м 2) , R = OX = 10 м Найти: ОО 1 Решение: 1. Любое сечение шара плоскостью есть круг. Sсеч= πr 2 36 π=π r 2 => r 2= 36 (м 2) 2. ∆ОО 1 Х – прямоугольный ОО 1= h , O 1 X = r , OX = R H 2= R 2 - r 2 - т. Пифагора H 2=100 – 36 =64, h = 8 м Ответ: h = 8 м

Применение в природе

В быту.

Вставьте пропущенные слова: От какого греческого слова происходят слова «шар» и «сфера» ? Ответ: «сфайра» Что называется шаром? Ответ: тело, которое состоит из всех точек пространства Что называется центром шара? Ответ: точка пространства, которая расположена на заданном расстоянии

Что называется радиусом сферы? Ответ: любой отрезок, соединяющий центр и какую-нибудь точку сферы Когда получается наибольший радиус сечения? Ответ: Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Второе определение шара? Ответ: тело, полученное от вращения полукруга вокруг диаметра как оси.