Shape Analysis for Low-level Code Hongseok Yang Seoul

Shape Analysis for Low-level Code Hongseok Yang (Seoul National University) (Joint work with Cristiano Calcagno, Dino Distefano and Peter O’Hearn)

Dream Automatically verify the memory safety of systems code, such as device derivers and memory managers. Challenges: 1. Pointer arithmetic. 2. Scalability. 3. Concurrency.

Our Analyzer Handles programs for dynamic memory management. n Experimental results (Pentium 3. 2 GHz, 4 GB) Found a hidden assumption of the K&R memory manager. These are “fixed” versions. n Proved memory safety and even partial correctness.

Sample Analysis Result Program: ans = malloc_bestfit_acyclic(n); Precondition: n¸ 2 Æ mls(freep, 0) Postcondition: (ans=0 Æ n¸ 2 Æ mls(freep, 0)) Ç (n¸ 2 Æ nd(ans, q’, n) * mls(freep, q’) * mls(q’, 0))

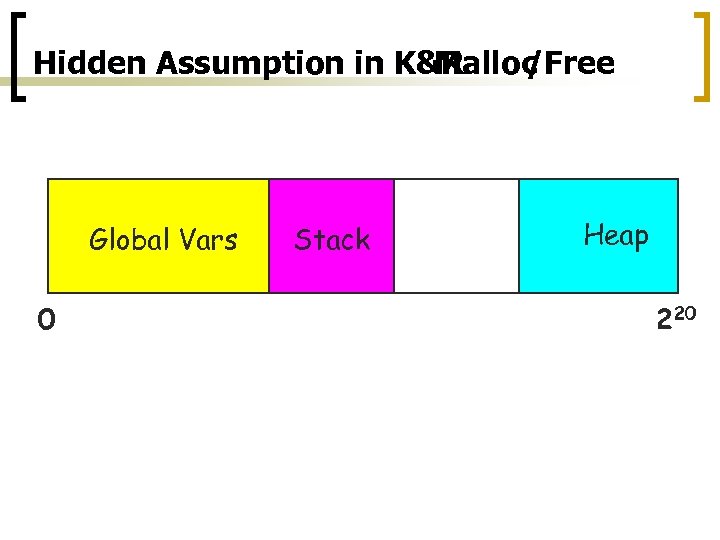Hidden Assumption in K&R Malloc /Free Global Vars 0 Stack Heap 220

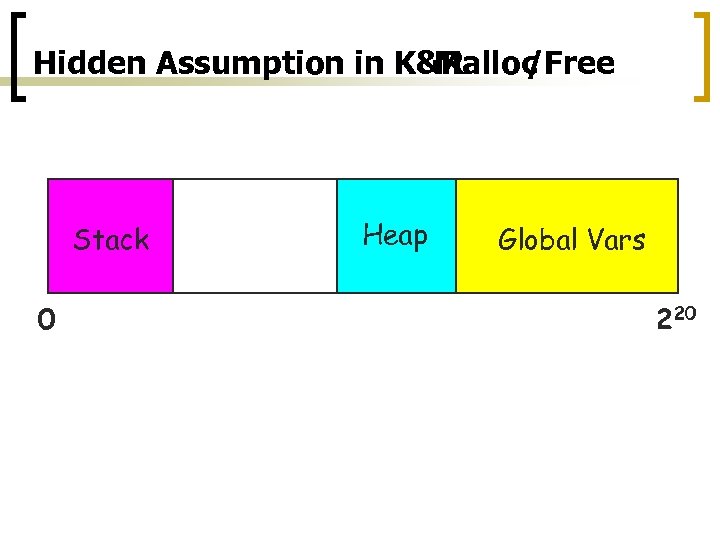Hidden Assumption in K&R Malloc /Free Stack 0 Heap Global Vars 220

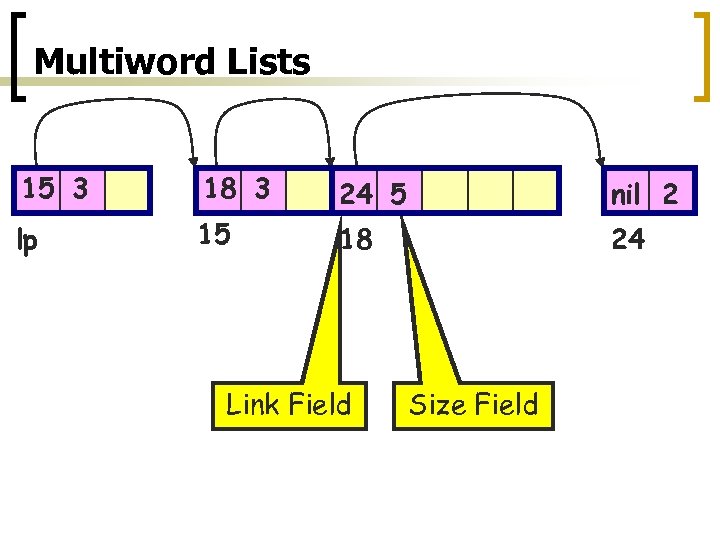Multiword Lists 15 3 18 3 24 5 nil 2 lp 15 18 24 Link Field Size Field

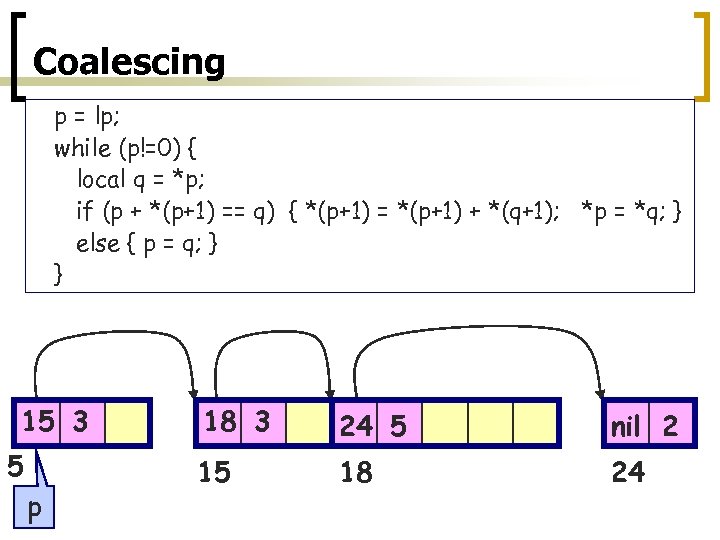Coalescing p = lp; while (p!=0) { local q = *p; if (p + *(p+1) == q) { *(p+1) = *(p+1) + *(q+1); *p = *q; } else { p = q; } } 15 3 5 p 18 3 24 5 nil 2 15 18 24

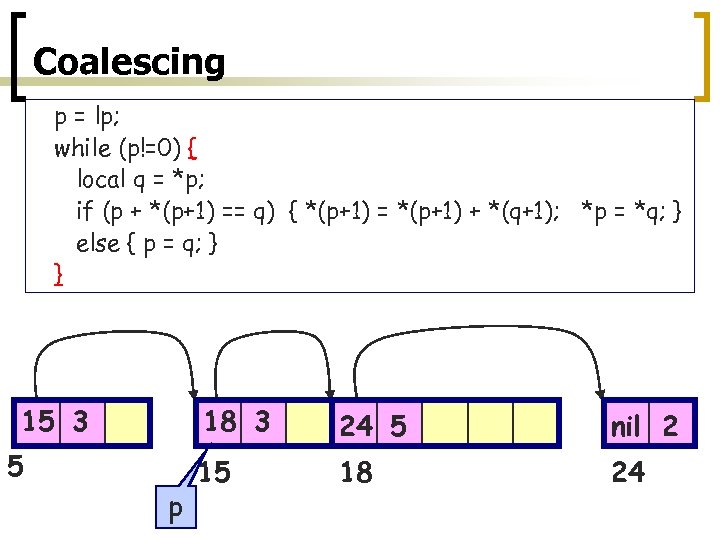Coalescing p = lp; while (p!=0) { local q = *p; if (p + *(p+1) == q) { *(p+1) = *(p+1) + *(q+1); *p = *q; } else { p = q; } } 15 3 18 3 5 p 24 5 nil 2 15 18 24

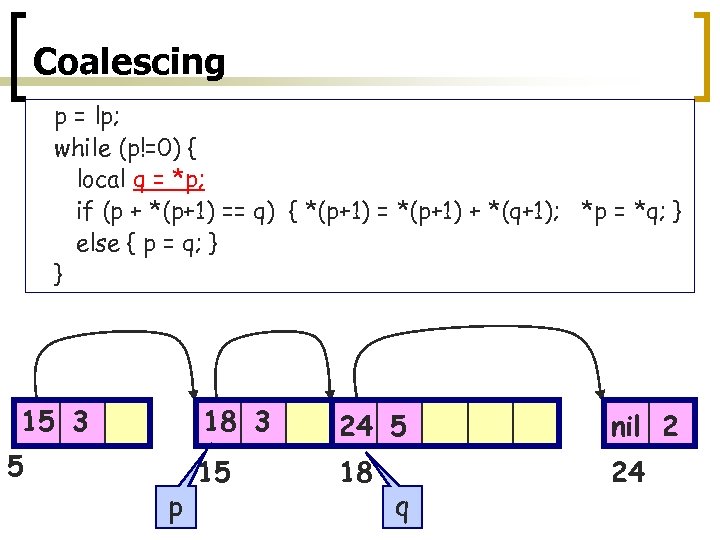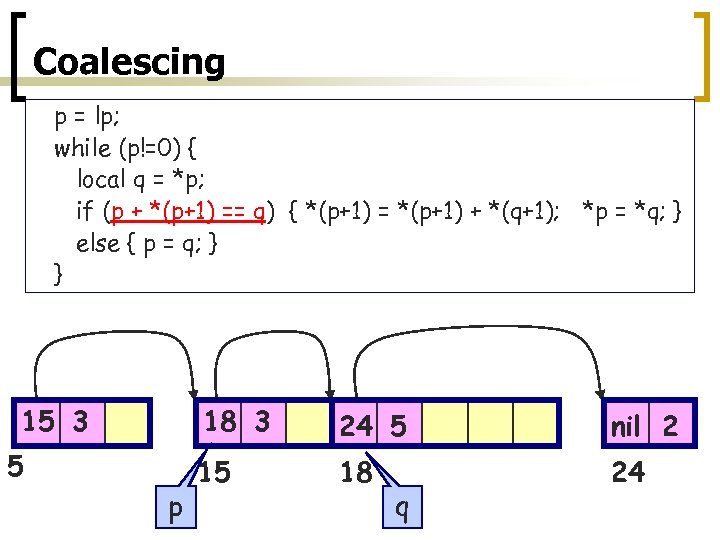Coalescing p = lp; while (p!=0) { local q = *p; if (p + *(p+1) == q) { *(p+1) = *(p+1) + *(q+1); *p = *q; } else { p = q; } } 15 3 18 3 5 p 24 5 nil 2 15 18 24 q

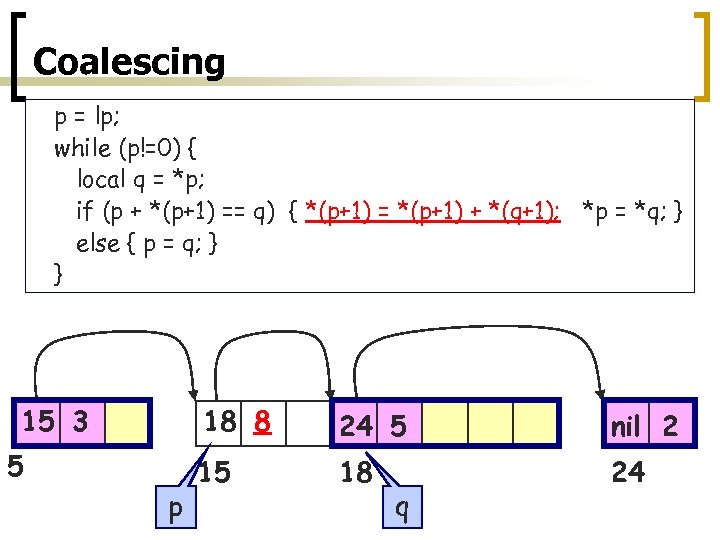Coalescing p = lp; while (p!=0) { local q = *p; if (p + *(p+1) == q) { *(p+1) = *(p+1) + *(q+1); *p = *q; } else { p = q; } } 15 3 18 8 5 p 24 5 nil 2 15 18 24 q

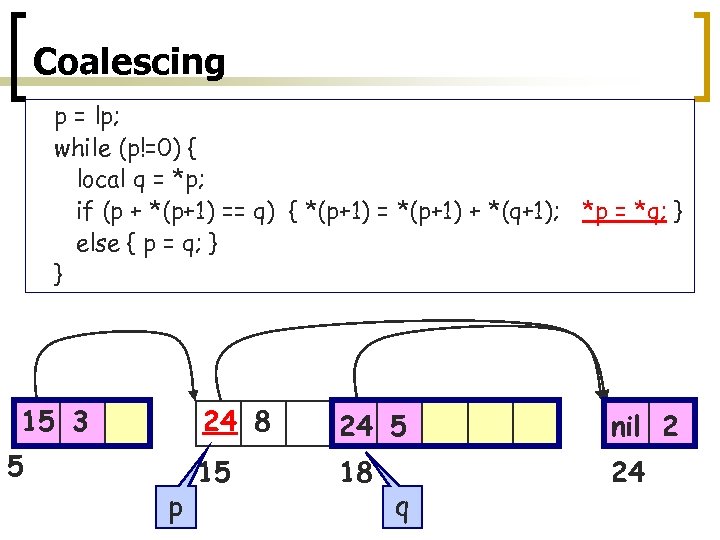Coalescing p = lp; while (p!=0) { local q = *p; if (p + *(p+1) == q) { *(p+1) = *(p+1) + *(q+1); *p = *q; } else { p = q; } } 15 3 24 8 5 p 24 5 nil 2 15 18 24 q

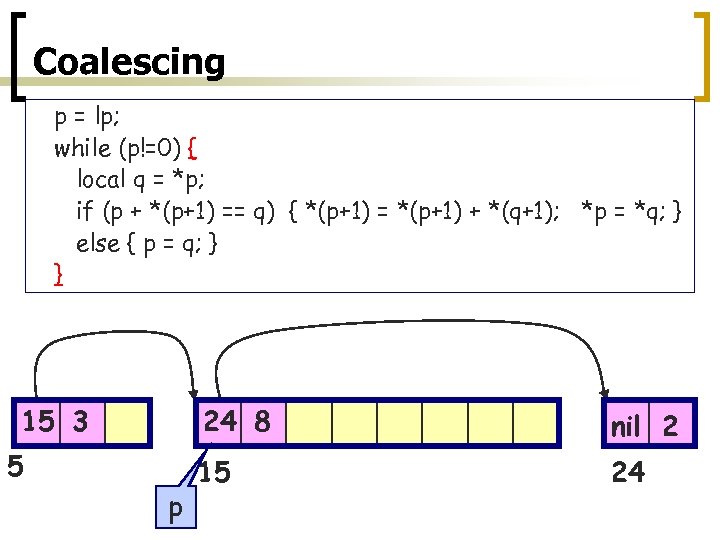Coalescing p = lp; while (p!=0) { local q = *p; if (p + *(p+1) == q) { *(p+1) = *(p+1) + *(q+1); *p = *q; } else { p = q; } } 15 3 24 8 5 p nil 2 15 24

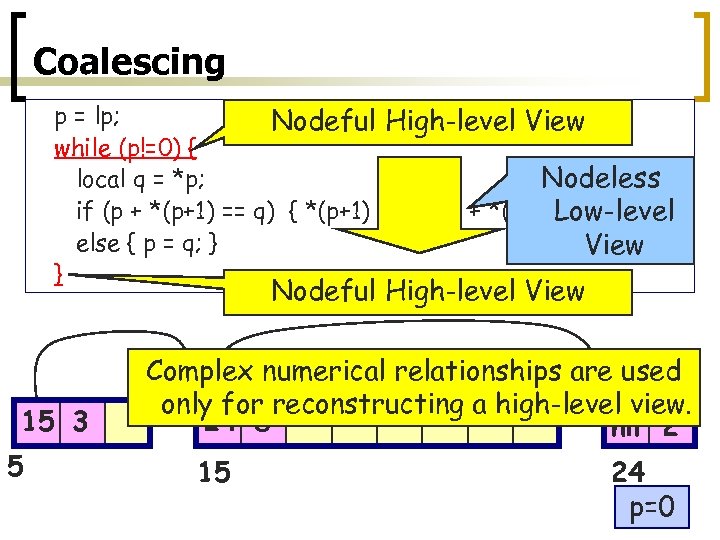Coalescing p = lp; Nodeful High-level View while (p!=0) { Nodeless local q = *p; if (p + *(p+1) == q) { *(p+1) = *(p+1) + *(q+1); *p = *q; } Low-level else { p = q; } View } Nodeful High-level View 15 3 5 Complex numerical relationships are used only for reconstructing a high-level view. 24 8 nil 2 15 24 p=0

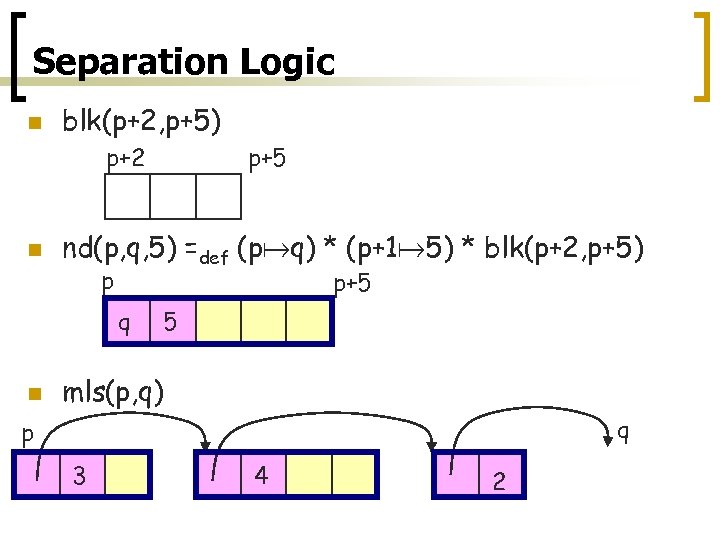Separation Logic n blk(p+2, p+5) p+2 n p+5 nd(p, q, 5) =def (p q) * (p+1 5) * blk(p+2, p+5) p p+5 q n 5 mls(p, q) q p 3 4 2

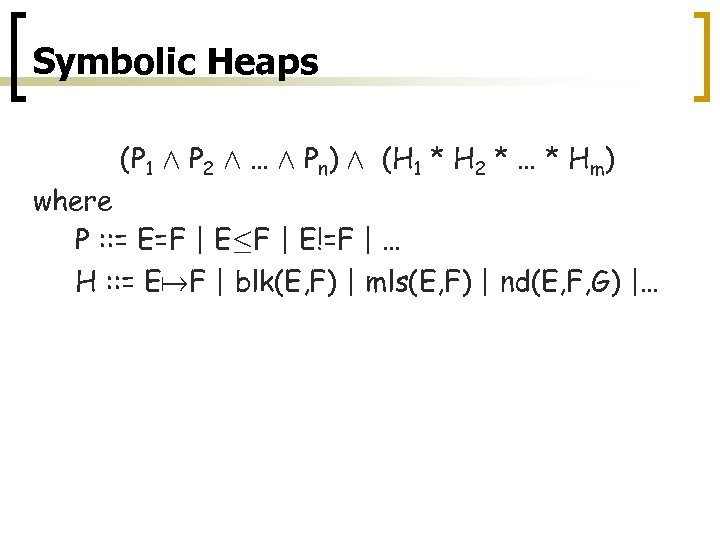Symbolic Heaps 9 x’, y’. (P 1 Æ P 2 Æ … Æ Pn) Æ (H 1 * H 2 * … * Hm) where P : : = E=F | E·F | E!=F | … H : : = E F | blk(E, F) | mls(E, F) | nd(E, F, G) |…

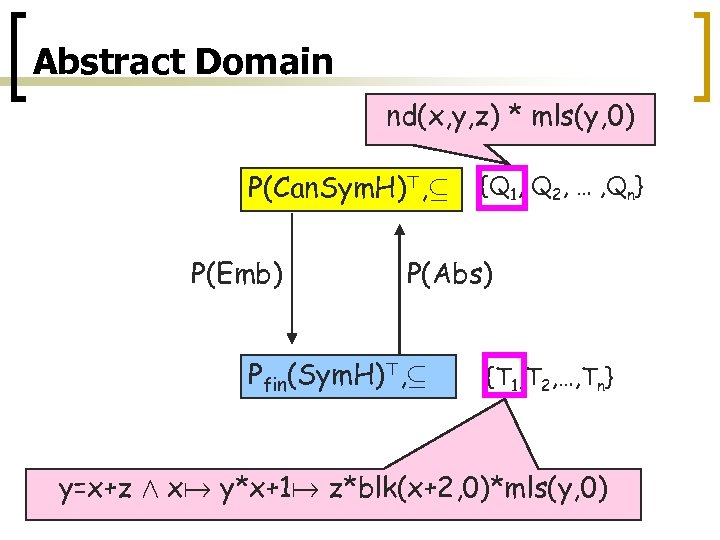Abstract Domain nd(x, y, z) * mls(y, 0) P(Can. Sym. H)>, µ P(Emb) {Q 1, Q 2, … , Qn} P(Abs) Pfin(Sym. H)>, µ {T 1, T 2, …, Tn} y=x+z Æ x y*x+1 z*blk(x+2, 0)*mls(y, 0)

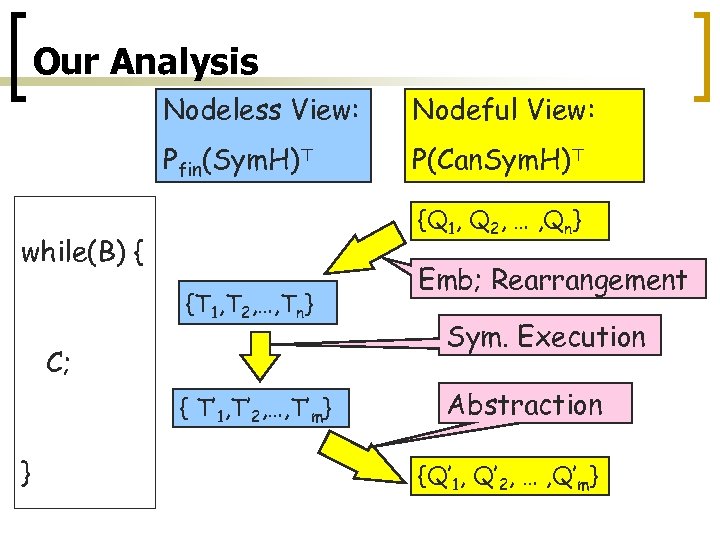Our Analysis Nodeless View: Nodeful View: Pfin(Sym. H)> P(Can. Sym. H)> {Q 1, Q 2, … , Qn} while(B) { {T 1, T 2, …, Tn} C; { T’ 1, T’ 2, …, T’m} } Emb; Rearrangement Sym. Execution Abstraction {Q’ 1, Q’ 2, … , Q’m}

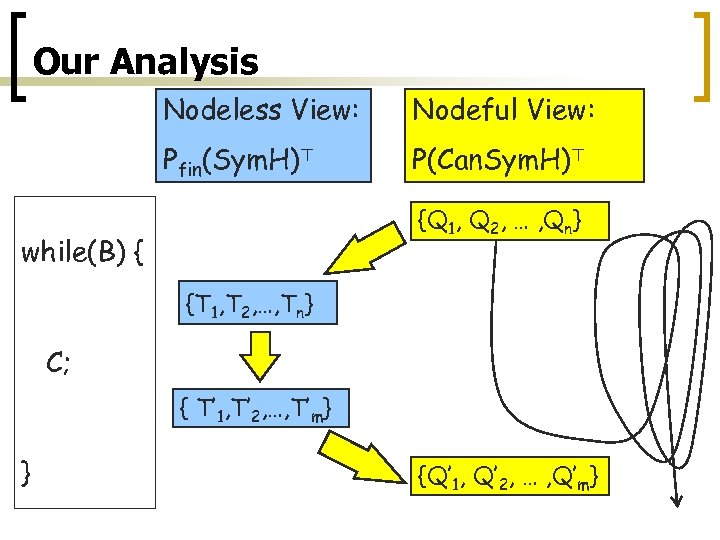Our Analysis Nodeless View: Nodeful View: Pfin(Sym. H)> P(Can. Sym. H)> {Q 1, Q 2, … , Qn} while(B) { {T 1, T 2, …, Tn} C; { T’ 1, T’ 2, …, T’m} } {Q’ 1, Q’ 2, … , Q’m}

Analysis «C¬ : Pfin(Sym. H)> ! Pfin(Sym. H)> «A¬d = P(Sym. Exec(A) o Rearrange(A))d «while b C¬d = Fix. Comp(P(Abs) o F) where F : P(Can. Sym. Heaps) ! P(Can. Sym. Heaps) F(d’) = P(Abs)(d [ «C¬d’)

Analysis «C¬ : Pfin(Sym. H)> ! Pfin(Sym. H)> «A¬d = (P(Sym. Exec(A)) o lift(Rearrange(A)))d «while b C¬d = Fix. Comp(P(Abs) o F) where F : P(Can. Sym. Heaps) ! P(Can. Sym. Heaps) Sym. Exec(A) : Rearrange(A) : F(d’) = P(Abs)(d [ «C¬d’) Proof Rules in Sep. Log. Unrolling of mls and nd

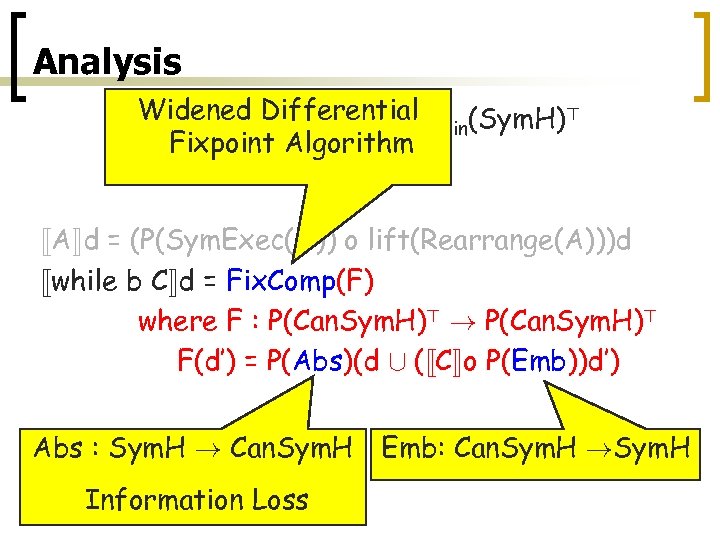Analysis Widened Differential P (Sym. H)> «C¬ : Pfin(Sym. H)> ! fin Fixpoint Algorithm «A¬d = (P(Sym. Exec(A)) o lift(Rearrange(A)))d «while b C¬d = Fix. Comp(F) where F : P(Can. Sym. H)> ! P(Can. Sym. H)> F(d’) = P(Abs)(d [ ( «C¬o P(Emb))d’) Abs : Sym. H ! Can. Sym. H Information Loss Emb: Can. Sym. H !Sym. H

Abstraction Function Abs : Sym. H ! Can. Sym. H 1. 2. 3. Package all nodes. Drop numerical relationships. Combine two connected multiword lists. (5 · x+x Æ p+3=z’) Æ (p q’ * p+1 3 * blk(p+2, z’) * mls(q’, 0))

Abstraction Function Abs : Sym. H ! Can. Sym. H 1. 2. 3. Package all nodes. Drop numerical relationships. Combine two connected multiword lists. (5 · x+x Æ p+3=z’) Æ (nd(p, q’, 3) * mls(q’, 0))

Abstraction Function Abs : Sym. H ! Can. Sym. H 1. 2. 3. Package all nodes. Drop numerical relationships. Combine two connected multiword lists. (5 · x+x Æ p+3=z’) Æ (nd(p, q’, 3) * mls(q’, 0)) * mls(q’, 0) * r 4)

Abstraction Function Abs : Sym. H ! Can. Sym. H 1. 2. 3. Package all nodes. Drop numerical relationships. Combine two connected multiword lists. (5 · x+x Æ p+3=z’) Æ (nd(p, q’, 3) * mls(q’, 0)) * mls(q’, 0) * true)

Abstraction Function Abs : Sym. H ! Can. Sym. H 1. 2. 3. Package all nodes. Drop numerical relationships. Combine two connected multiword lists. (5 · x+x Æ p+3=z’) Æ (nd(p, q’, 3) * mls(q’, 0))

Abstraction Function Abs : Sym. H ! Can. Sym. H 1. 2. 3. Package all nodes. Drop numerical relationships. Combine two connected multiword lists. (nd(p, q’, 3) * mls(q’, 0))

Abstraction Function Abs : Sym. H ! Can. Sym. H 1. 2. 3. Package all nodes. Drop numerical relationships. Combine two connected multiword lists. mls(p, 0)

Abstraction Function Abs : Sym. H ! Can. Sym. H 1. 2. 3. Package all nodes. Drop numerical relationships. Combine two connected multiword lists. Precondition: true … (x x’, s) * blk(x+2, x+s) x x’ x+2 s x+s Ã … nd(x, x’, s) x+s x x’ s

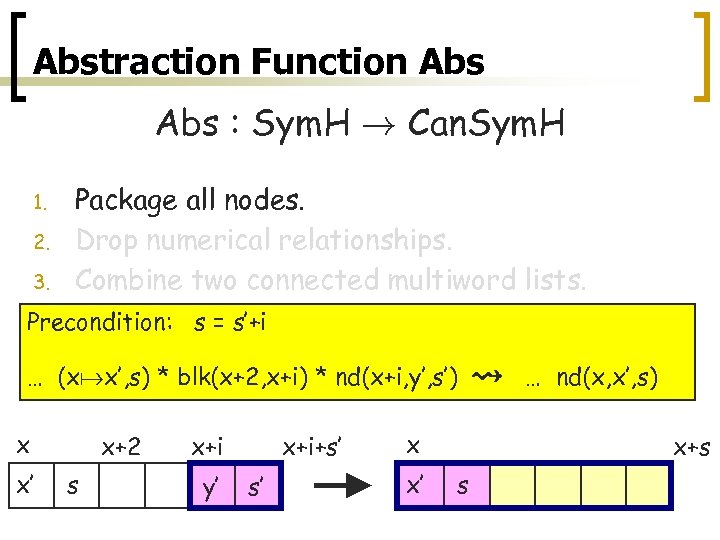
Abstraction Function Abs : Sym. H ! Can. Sym. H 1. 2. 3. Package all nodes. Drop numerical relationships. Combine two connected multiword lists. Precondition: s = s’+i … (x x’, s) * blk(x+2, x+i) * nd(x+i, y’, s’) x x’ x+2 s x+i y’ x+i+s’ s’ x x’ Ã … nd(x, x’, s) x+s s

… Coalescing mls(lp, p) * mls(p, 0) while (p!=0){local q=p*; p!=0 Æ mls(lp, p) * p q, s’ * blk(p+2, p+s’) * mls(q, 0) if (p + *(p+1) == q) { p!=0 Æ p+s’=q Æ mls(lp, p)*p q, s’ * blk(p+2, p+s’) * mls(q, 0) *(p+1) = *(p+1) + *(q+1); p!=0Æp+s’=qÆmls(lp, p)* p q, s’+t’ * blk(p+2, p+s’) *q r’, t’*blk(q+2, q+t’)*mls(r’, 0) *p = *q; p!=0Æp+s’=qÆmls(lp, p)*p r’, s’+t’*blk(p+2, p+s’)*q r’, t’*blk(q+2, q+t’)*mls(r’, 0) } else { p = *p; } p!=0Æp+s’=qÆmls(lp, p)*p r’, s’+t’*blk(p+2, p+s’)*q r’, t’*blk(q+2, q+t’)*mls(r’, 0) }

… Coalescing mls(lp, p) * mls(p, 0) while (p!=0){local q=p*; p!=0 Æ mls(lp, p) * p q, s’ * blk(p+2, p+s’) * mls(q, 0) if (p + *(p+1) == q) { p!=0 Æ p+s’=q Æ mls(lp, p)*p q, s’ * blk(p+2, p+s’) * mls(q, 0) *(p+1) = *(p+1) + *(q+1); p!=0Æp+s’=qÆmls(lp, p)* p q, s’+t’ * blk(p+2, p+s’) *q r’, t’*blk(q+2, q+t’)*mls(r’, 0) *p = *q; p!=0Æp+s’=qÆmls(lp, p)*p r’, s’+t’*blk(p+2, p+s’)*q r’, t’*blk(q+2, q+t’)*mls(r’, 0) } else { p = *p; } p!=0Æp+s’=q’Æmls(lp, p)*p r’, s’+t’*blk(p+2, p+s’)*q’ r’, t’*blk(q’+2, q’+t’)*mls(r’, 0) }

… Coalescing mls(lp, p) * mls(p, 0) while (p!=0){local q=p*; p!=0 Æ mls(lp, p) * p q, s’ * blk(p+2, p+s’) * mls(q, 0) if (p + *(p+1) == q) { p!=0 Æ p+s’=q Æ mls(lp, p)*p q, s’ * blk(p+2, p+s’) * mls(q, 0) *(p+1) = *(p+1) + *(q+1); p!=0Æp+s’=qÆmls(lp, p)* p q, s’+t’ * blk(p+2, p+s’) *q r’, t’*blk(q+2, q+t’)*mls(r’, 0) *p = *q; p!=0Æp+s’=qÆmls(lp, p)*p r’, s’+t’*blk(p+2, p+s’)*q r’, t’*blk(q+2, q+t’)*mls(r’, 0) } else { p = *p; } p!=0Æp+s’=q’Æmls(lp, p)*p r’, s’+t’*blk(p+2, p+s’)*nd(q’, r’, t’) } *mls(r’, 0)

… Coalescing mls(lp, p) * mls(p, 0) while (p!=0){local q=p*; p!=0 Æ mls(lp, p) * p q, s’ * blk(p+2, p+s’) * mls(q, 0) if (p + *(p+1) == q) { p!=0 Æ p+s’=q Æ mls(lp, p)*p q, s’ * blk(p+2, p+s’) * mls(q, 0) *(p+1) = *(p+1) + *(q+1); p!=0Æp+s’=qÆmls(lp, p)* p q, s’+t’ * blk(p+2, p+s’) *q r’, t’*blk(q+2, q+t’)*mls(r’, 0) *p = *q; p!=0Æp+s’=qÆmls(lp, p)*p r’, s’+t’*blk(p+2, p+s’)*q r’, t’*blk(q+2, q+t’)*mls(r’, 0) } else { p = *p; } p!=0Æp+s’=q’Æmls(lp, p)*nd(p, r’, s’+t’)* } *mls(r’, 0)

… Coalescing mls(lp, p) * mls(p, 0) while (p!=0){local q=p*; p!=0 Æ mls(lp, p) * p q, s’ * blk(p+2, p+s’) * mls(q, 0) if (p + *(p+1) == q) { p!=0 Æ p+s’=q Æ mls(lp, p)*p q, s’ * blk(p+2, p+s’) * mls(q, 0) *(p+1) = *(p+1) + *(q+1); p!=0Æp+s’=qÆmls(lp, p)* p q, s’+t’ * blk(p+2, p+s’) *q r’, t’*blk(q+2, q+t’)*mls(r’, 0) *p = *q; p!=0Æp+s’=qÆmls(lp, p)*p r’, s’+t’*blk(p+2, p+s’)*q r’, t’*blk(q+2, q+t’)*mls(r’, 0) } else { p = *p; } } mls(lp, p)*nd(p, r’, s’+t’)* *mls(r’, 0)

… Coalescing mls(lp, p) * mls(p, 0) while (p!=0){local q=p*; p!=0 Æ mls(lp, p) * p q, s’ * blk(p+2, p+s’) * mls(q, 0) if (p + *(p+1) == q) { p!=0 Æ p+s’=q Æ mls(lp, p)*p q, s’ * blk(p+2, p+s’) * mls(q, 0) *(p+1) = *(p+1) + *(q+1); p!=0Æp+s’=qÆmls(lp, p)* p q, s’+t’ * blk(p+2, p+s’) *q r’, t’*blk(q+2, q+t’)*mls(r’, 0) *p = *q; p!=0Æp+s’=qÆmls(lp, p)*p r’, s’+t’*blk(p+2, p+s’)*q r’, t’*blk(q+2, q+t’)*mls(r’, 0) } else { p = *p; } } mls(lp, p)*mls(p, 0)

Theorem. Proverfor “Q ` Q 2” 1 without prover with prover malloc_K&R about 20 hours 502. 23 secs free_K&R 23. 844 secs 9. 69 secs

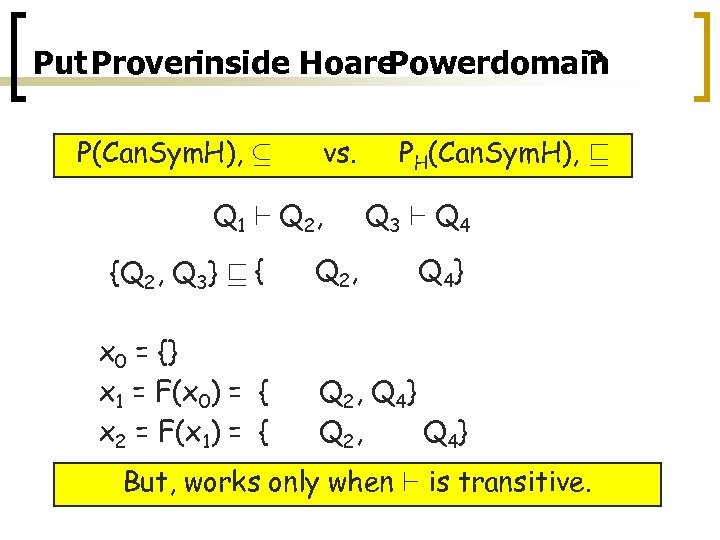Put Proverinside Hoare Powerdomain ? P(Can. Sym. H), µ vs. Q 1 ` Q 2, PH(Can. Sym. H), v Q 3 ` Q 4 {Q 2, Q 3} v {Q 1, Q 2, Q 3, Q 4} x 0 = {} x 1 = F(x 0) = {Q 1, Q 2, Q 4} x 2 = F(x 1) = {Q 1, Q 2, Q 3, Q 4} But, works only when ` is transitive.

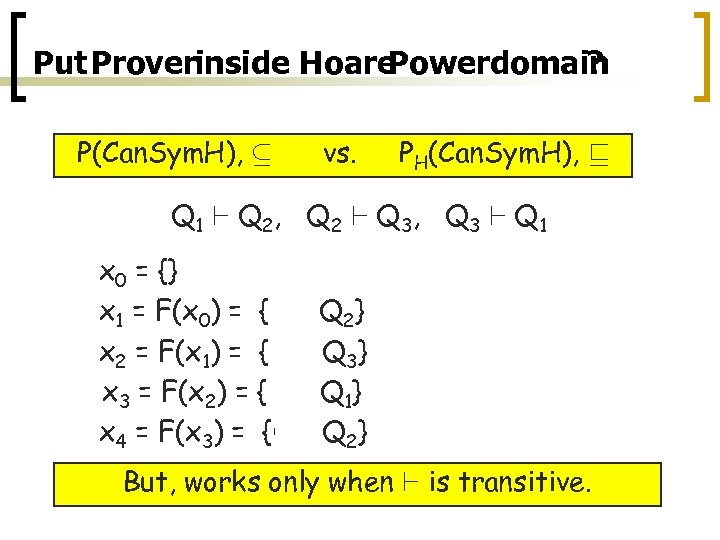Put Proverinside Hoare Powerdomain ? P(Can. Sym. H), µ vs. PH(Can. Sym. H), v Q 1 ` Q 2, Q 2 ` Q 3, Q 3 ` Q 1 x 0 = {} x 1 = F(x 0) = {Q 1, Q 2} x 2 = F(x 1) = {Q 2, Q 3} x 3 = F(x 2) = {Q 3, Q 1} x 4 = F(x 3) = {Q 1, Q 2} But, works only when ` is transitive.

Put Proverinside Widening! r : P(Can. Sym. H) £ P(Can. Sym. H) ! P(Can. Sym. H) x 0 r x 1 =def x 0 [ { Q 2 x 1 | 8 Q’ 2 x 0. Q ` Q’ } x 0 = {} x 1 = x 0 r F(x 0) x 2 = x 1 r F(x 1) xn+1 = xn r F(xn) … x 0 µ x 1 µ x 2 µ x 3 …

Add Differencing F : P(Can. Sym. H) ! P(Can. Sym. H) x. Nonstandard 0 = {} Fixpoint Algorithm: x • = NOT y = {Q 1} x 0 r. F({}) µ (x 1 r y). x 2 = x 1 r. F({Q 1}) = {Q 1, Q 2} • NOT F(wdfix F) µ wdfix F. x 3 = x 2 r. F({Q 1, Q 2}) = {Q 1, Q 2, Q 3} x 4 = NOT (F(wdfix F)), Q 2, Q 3} x 3 r. F({Q 1, Q 2, Q 3}) = {Q 1 µ (wdfix xn+1 = xnr. F(yn), yn+1 = xn+1 -xn F)

Soundness Analysis results can be compiled into separation-logic proofs.

Widened Differential Fixpoint. Algo. «while (*) C¬d 0 = ? ? x 0 = d 0 x 1 = x 0 r F(x 0) x 2 = x 1 r F(y 1) x 3 = x 2 r F(y 2) = x 2 y 1 = x 1 – x 0 y 2 = x 2 – x 1 (x 3) µ (d 0) [ (y 1) [ (y 2) (x 3 (d 0) [ r F(y )) [ F(y 2) x 3 =)d 0 r F(d 0) (F(d 01) r (F(y 1)) [ (F(y 2))

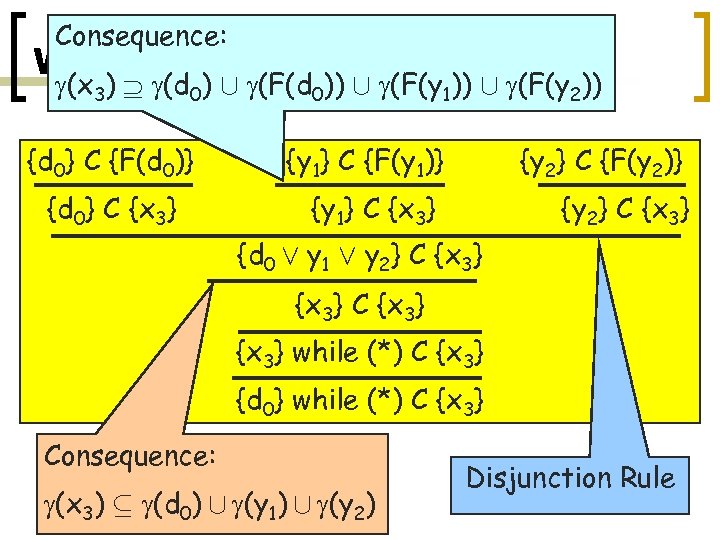Consequence: Widened Differential Fixpoint. Algo. (x 3) (d 0) [ (F(d 0)) [ (F(y 1)) [ (F(y 2)) {d 0} C {F(d 0)} {y 1} C {F(y 1)} {y 2} C {F(y 2)} {d 0} C {x 3} {y 1} C {x 3} {y 2} C {x 3} {d 0 Ç y 1 Ç y 2} C {x 3} while (*) C {x 3} {d 0} while (*) C {x 3} Consequence: (x 3) µ (d 0) [ (y 1) [ (y 2) Disjunction Rule