Shanghai Maritime University Chapter 1 What is stability?


Shanghai Maritime University

Chapter 1 What is stability? Stability is the ability of a vessel to return to its original condition or position after it has been disturbed by an outside force. Think: The differences between list and heel

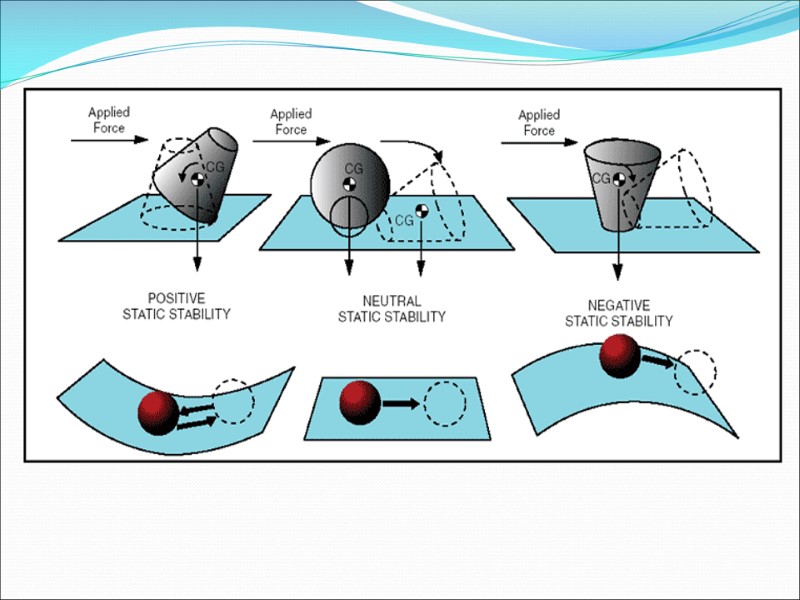
Types of initial stability Positive stability Neutral stability Negative stability
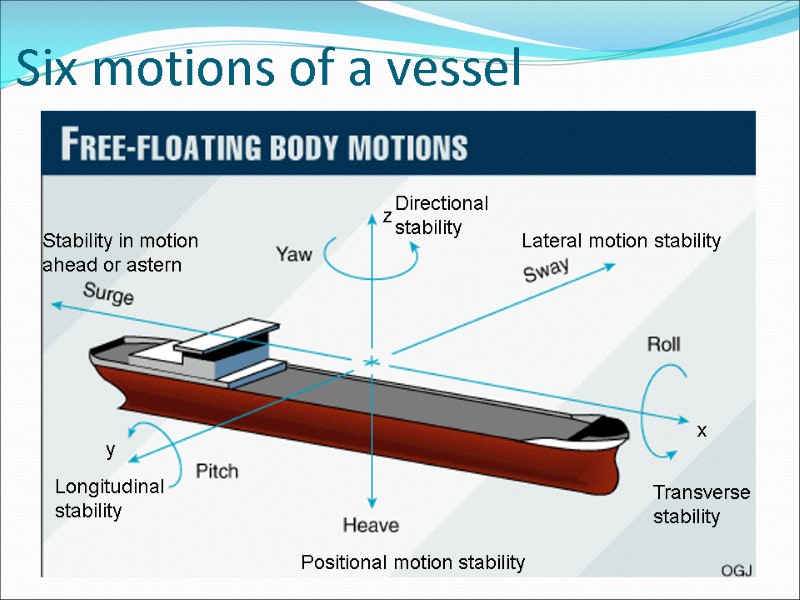
Six motions of a vessel x y z Transverse stability Longitudinal stability Directional stability Lateral motion stability Stability in motion ahead or astern Positional motion stability

Archimedes’ principle (law of floating bodies) Floating body displaces a weight of water equal to its own weight; that is, weight equals buoyancy.
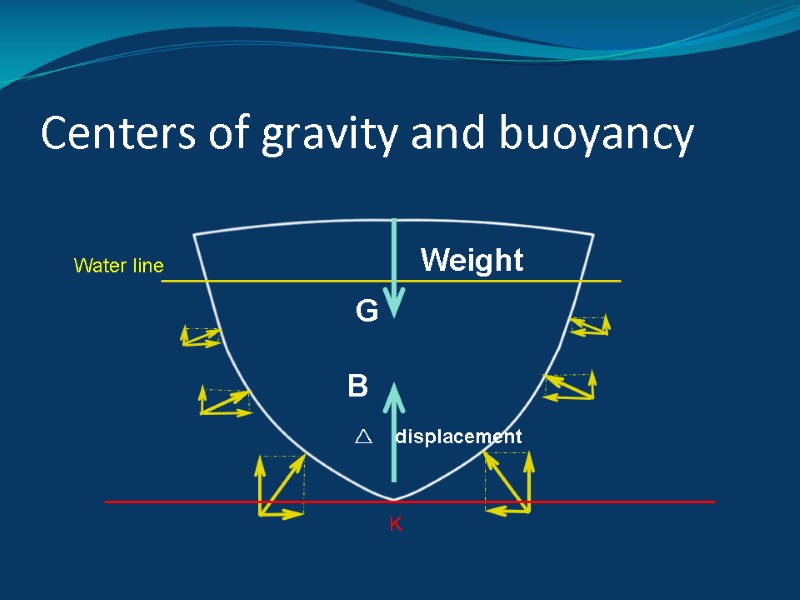
Centers of gravity and buoyancy G B Weight △ displacement K Water line
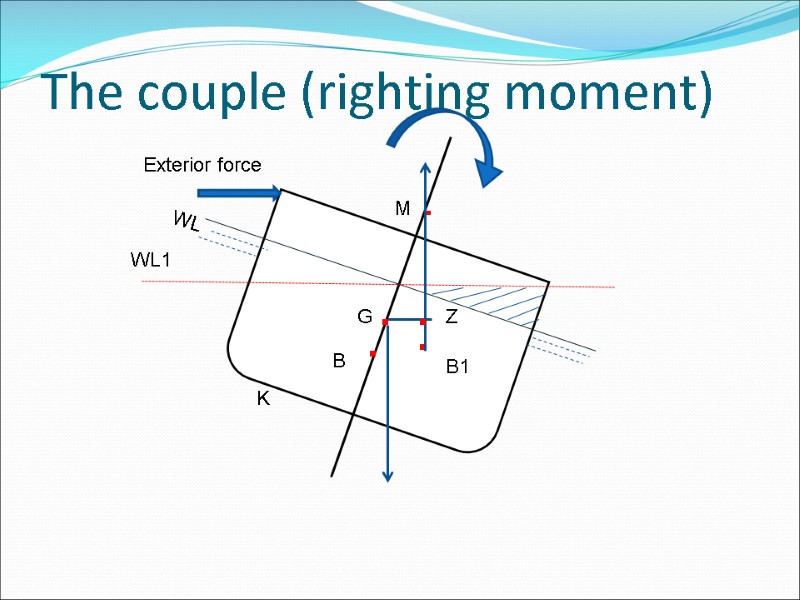
The couple (righting moment) WL WL1 . B . B1 . G K Exterior force M . . Z
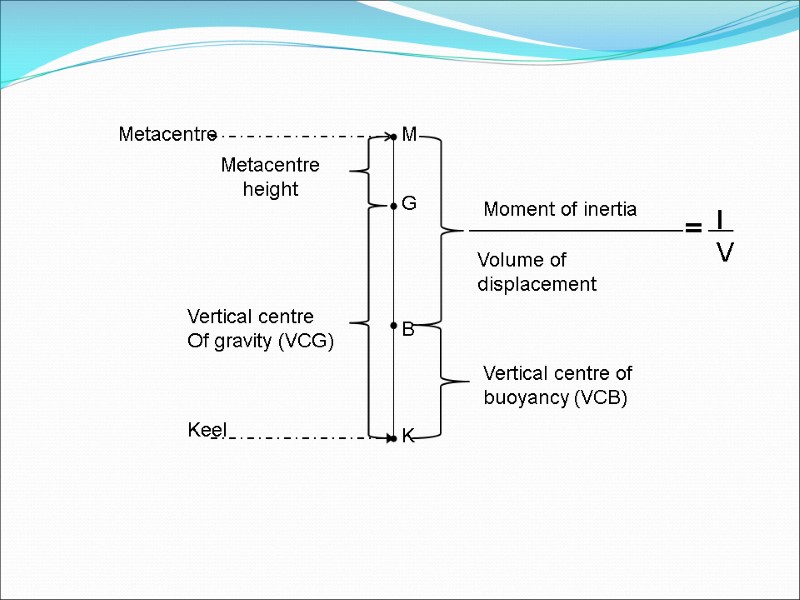
Vertical centre of buoyancy (VCB)
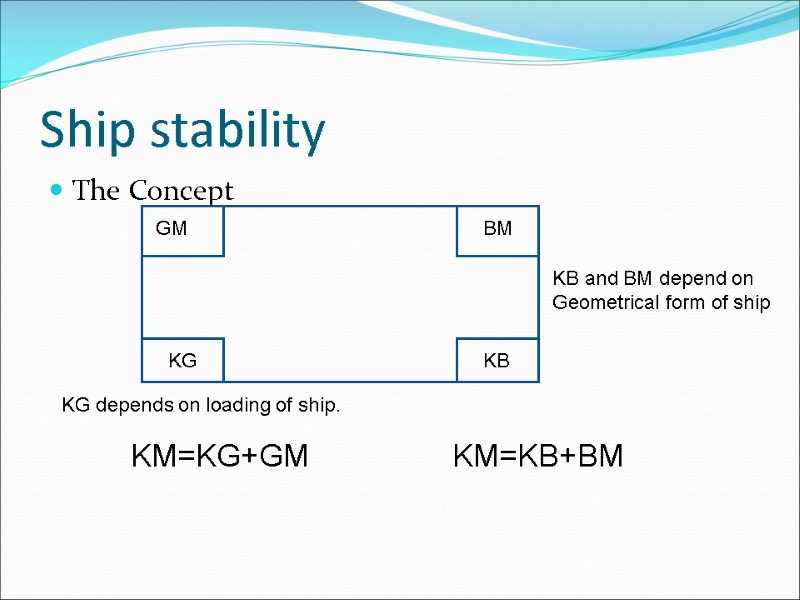
Ship stability The Concept KM=KG+GM KM=KB+BM KB and BM depend on Geometrical form of ship KG depends on loading of ship.
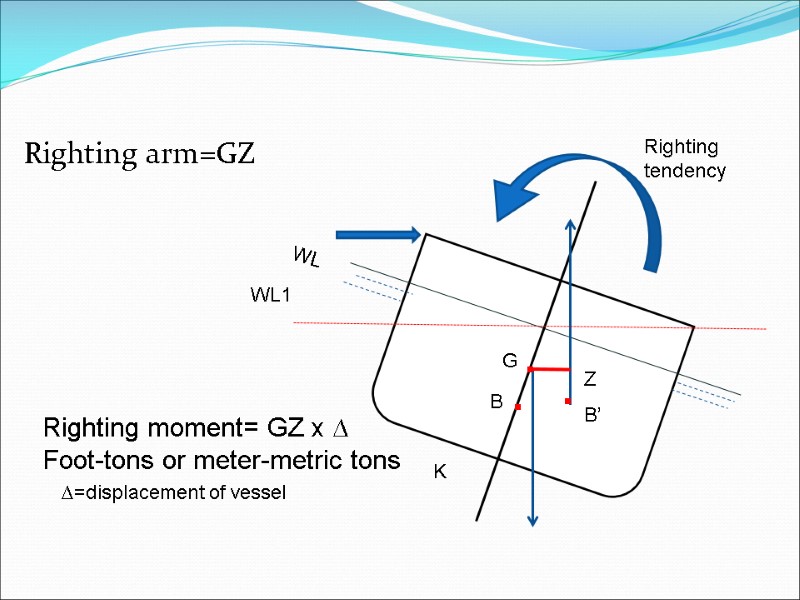
Righting arm=GZ B1 . . . Righting tendency Righting moment= GZ x ∆ Foot-tons or meter-metric tons ∆=displacement of vessel
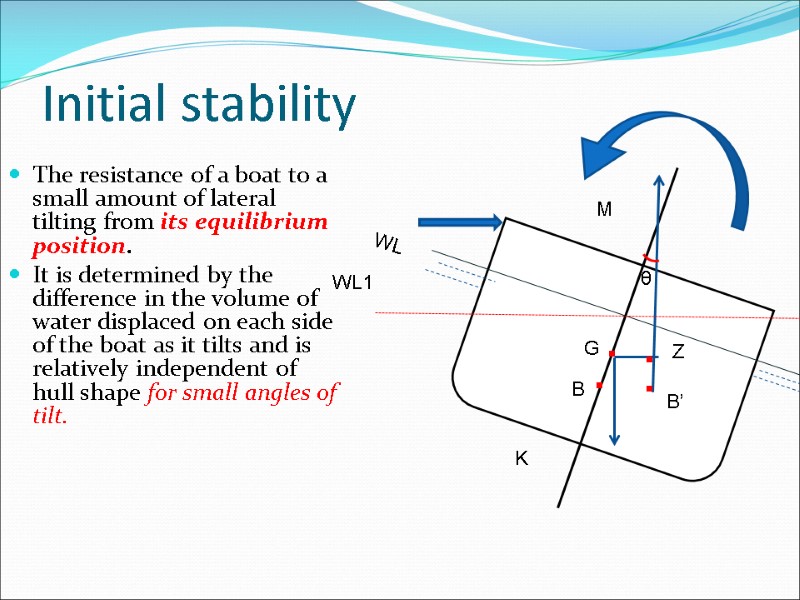
Initial stability The resistance of a boat to a small amount of lateral tilting from its equilibrium position. It is determined by the difference in the volume of water displaced on each side of the boat as it tilts and is relatively independent of hull shape for small angles of tilt. θ M .
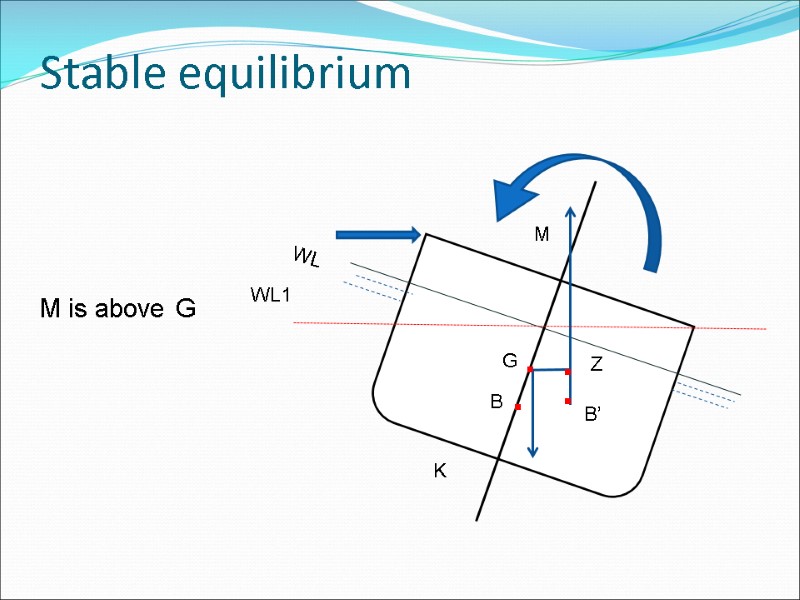
Stable equilibrium B G K . B’ Z WL WL1 . . M is above G . M
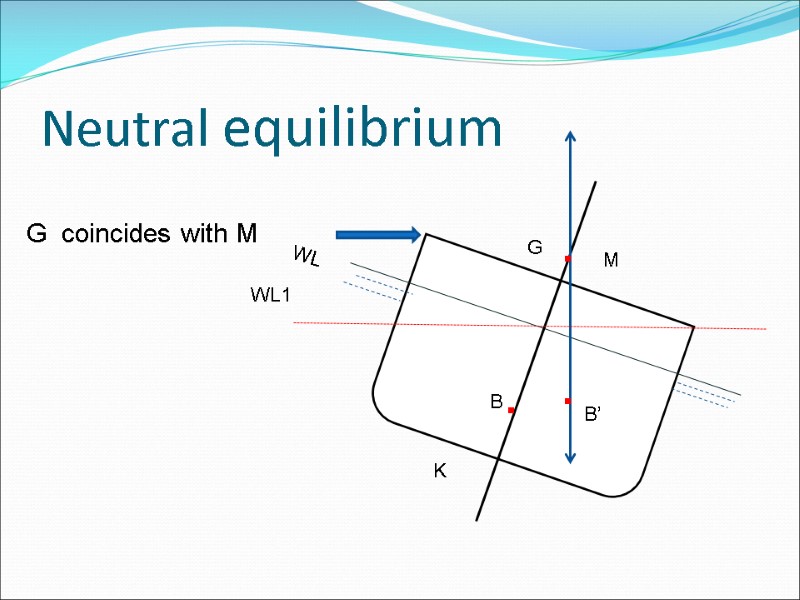
Neutral equilibrium M G coincides with M
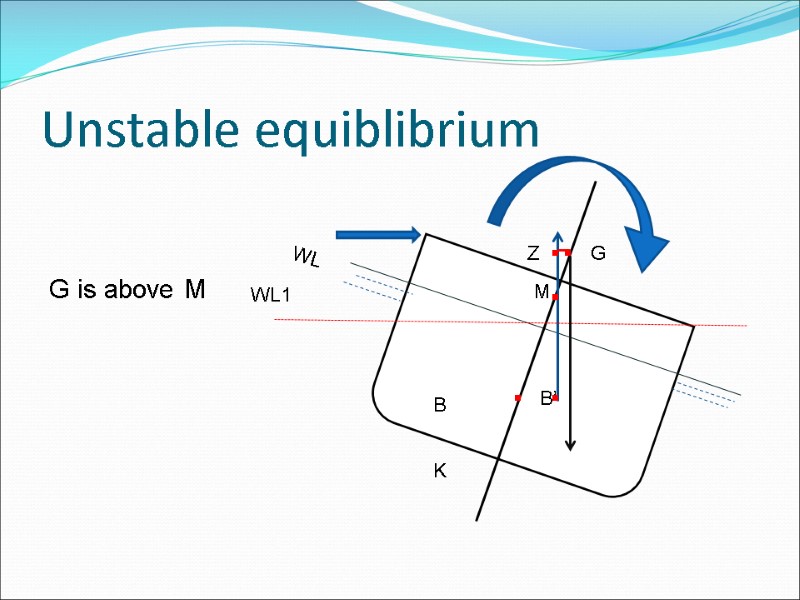
Unstable equiblibrium B G K . B’ Z WL WL1 . . . M G is above M .

Metacentric height (GM) θ M G Z B1 . GZ=GM sinθ Center line KM is the height of Metacenter. GM = KM - KG KM is available in hydrostatic data. KG is calculated by officer GM shows the initial stability of ship
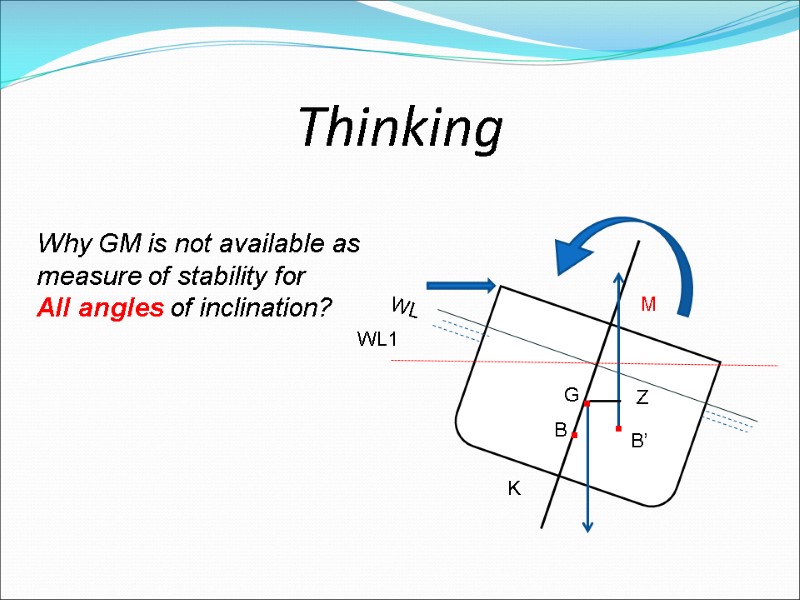
Thinking Why GM is not available as measure of stability for All angles of inclination? M
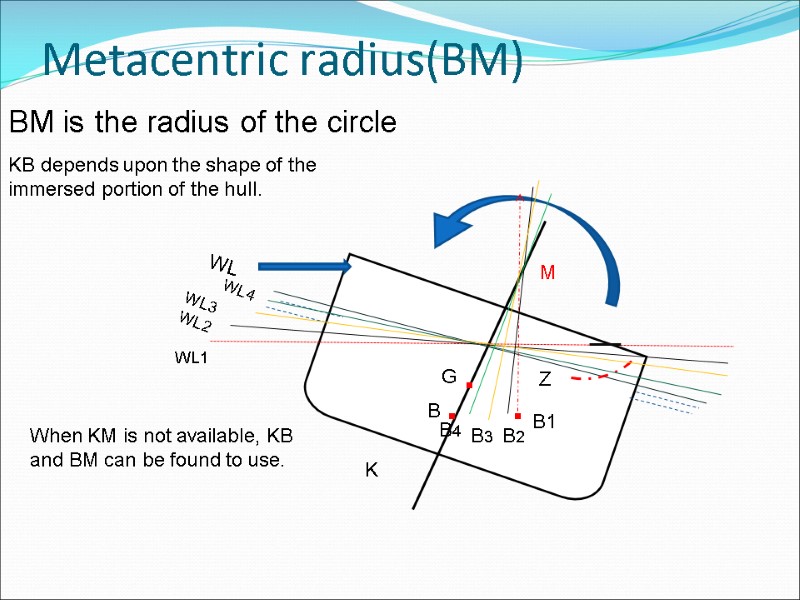
Metacentric radius(BM) M BM is the radius of the circle KB depends upon the shape of the immersed portion of the hull. B3 B4 WL3 B2 WL2 WL4 When KM is not available, KB and BM can be found to use.

Summary Stability is the tendency of a vessel to return to an erect position It can be determined for all angles of inclination by the value of the righting moment ∆GZ or righting arm GZ For small angle of inclination or initial stability, stability could be decided by metacentric height GM. While KM is not available, it maybe necessary to find KB and BM.

Chapter 2 Calculation of the Ship’s vertical center of gravity, KG This chapter we will learn how to caculate the vertical center of the ship when ship is loaded the main method of calculating KG
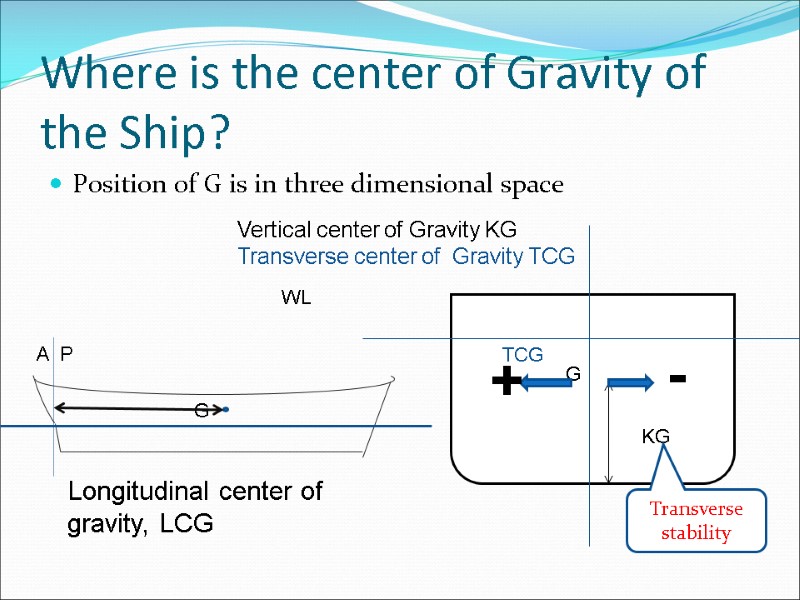
Where is the center of Gravity of the Ship? Position of G is in three dimensional space WL Vertical center of Gravity KG Transverse center of Gravity TCG Longitudinal center of gravity, LCG Transverse stability

Light ship KG and weight Light ship weight and KG are calculated by naval architects After loading , every weight (w) will affecting the original light ship KG and Weight. The theory of moment must be employed by officers Thinking How to get the original data of KG of the ship?

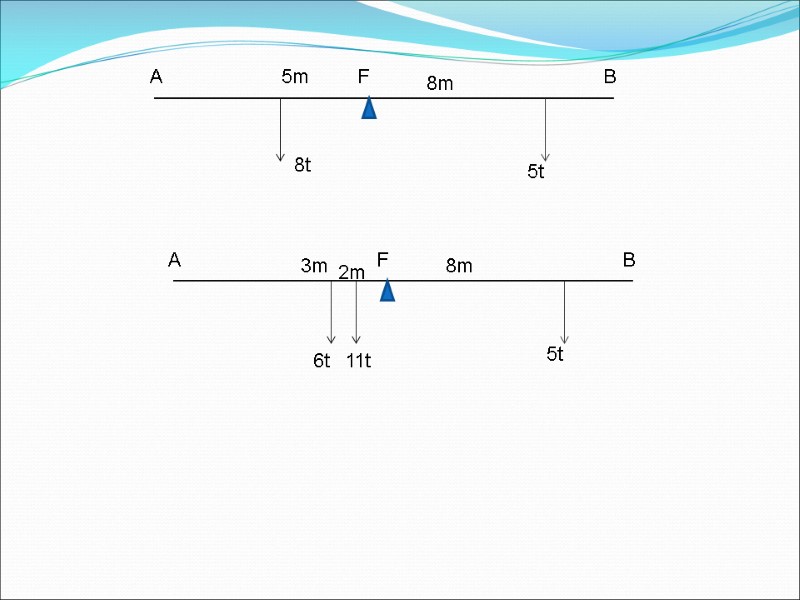
Definition of moment A moment is mathematical term that indicates something, (such as a weight, force, area, or volume), multiplied by its distance from a particular point or axis. A moment of a force (weight) can be expressed in force-distance units, like tons-meters
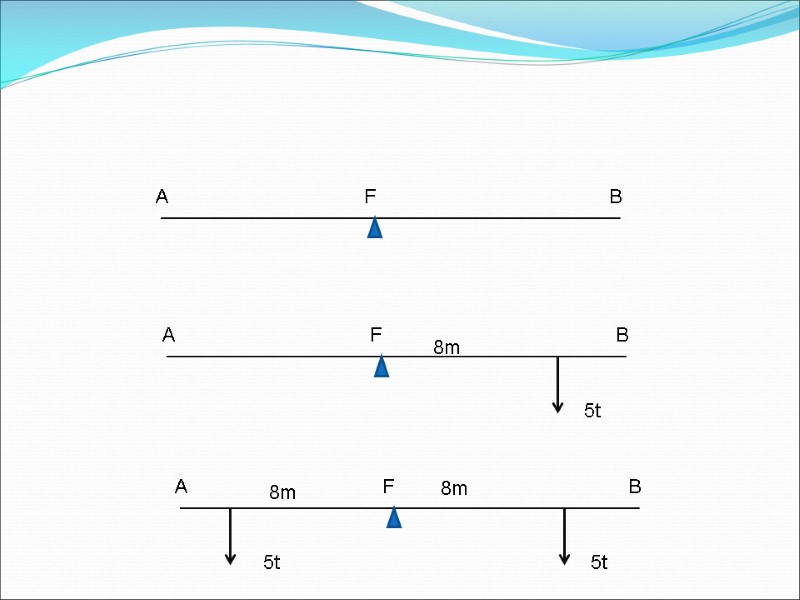
5t 8m 5t 5t 8m 8m
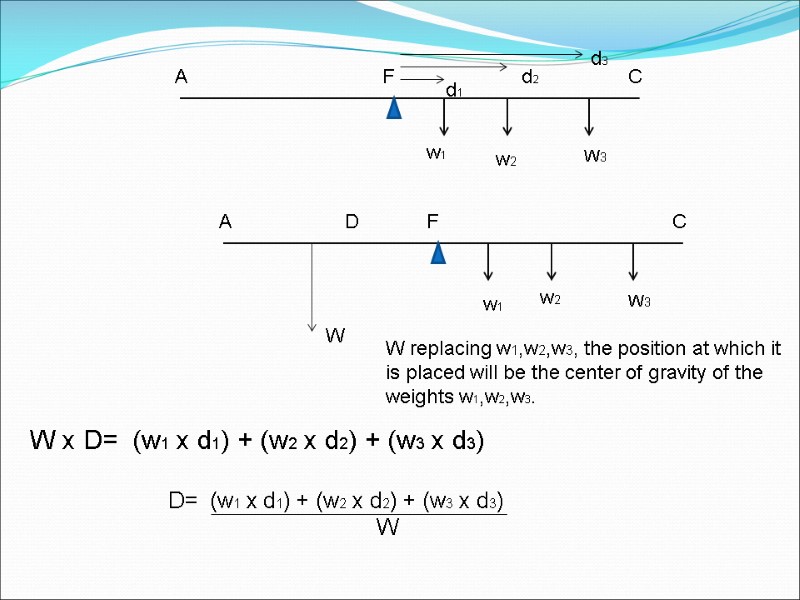
d2 d1 W replacing w1,w2,w3, the position at which it is placed will be the center of gravity of the weights w1,w2,w3. W x D= (w1 x d1) + (w2 x d2) + (w3 x d3) D= (w1 x d1) + (w2 x d2) + (w3 x d3) W

Taking moments about the keel K w1 w2 G G’ W W’ g1 g2 W is the weight of the ship W1,w2 are weights loaded/discharged Discharging weights W’= W-w1-w2 KG’=’=Sum of the moments about K Sum of the weights =W x KG-(w1 x Kg1)-(w2 x Kg2) W’

Example1 A vessel floating at her light draft displaces (weights) 5000 tons. The light ship KG is 20 feet above the keel. Two hundred tons are loaded 10 feet above the keel and 300 tons 5 feet above the light ship KG. What will be the position of the new KG? Dividing total moments by total weights KG=19.9 feet

Example2 The vessel in example 1 now has the following weights removed from the location listed below. Find the new KG after discharging. New KG= 103150 foot tons/4350 tons =23.7 feet

Example 3 A vessel is floating in ballast with a displacement of 32000 metric tons and a KG of 9.25 meters. 22,000 metric tons of ballast will be discharged with a KG of 8.5 meters. 600 tons of bunkers will be taken with a KG of 1.5 meters. 55,000 tons of grain will be loaded at a height of 9.7 meters. What will be the position of the new KG? Dividing total moments by total weights, KG= 9.81 meters

Exercise 1 A vessel of 13000 tons, KM10.5m (assumed constant), KG 9.5 m. loads: 400 tons KG 2.9; 900 tons KG 6.0 m; 1500 tons KG 10.6m; 2000 tones KG 8.3 m. she discharges: 700 tons KG 1.5 m; 300 tones KG 12.7m. Calculate the moment of statical stability if she is now heeled 8⁰. New KG=157700/16800=9.387 KM= 10.500 m GM= KM – KG=1.113 m Moment of statical stability= W x GM x sinθ = 16800 x 1.113 x sin 8 ⁰ = 2602 meter-tons

Exercise 2 A vessel displacing 5800 tons KM 7.0m KG 6.0m has to load a quantity of deck cargo KG 11.0 m. what is the maximum quantity that she can load so that her GM is not less than 0.75m. KM=7.00m new GM=0.75 Then, new KG=6.25 Then, w=305 tons GM now= KM-KG=7.0-6.0 m= 1.0 m GM required=0.75 m GG’=0.25m upward GG’=(w x d)/(W+w) 0.25=(w x 5)/(5800 + w) W= 305 tons

Taking moments about center of gravity GG’ is shift of center of gravity Calculating GG’ W is the vessel’s displacement before loading the weight w is the weight loaded d is the distance of the loaded weight from the old center of gravity

Example4 Suppose that on a 10,000-ton vessel with a KG of 25 feet, 200 tons are shifted vertically upwards a distance of 20 feet. Find the new KG for the vessel and the shift of G in terms of GG’. GG’= (200 tons X 20 feet )/(10,000 tons) = 0.4 feet up New KG= 25 feet + 0.4 feet = 25.4 feet

Example 5 The displacement of ship is 10,000 tons, he head of the jumbo boom is 80 feet above keel. If you lift a container of 30 tons, which is in the lower hold, 1 feet clear of the deck. If GG’ increase when you lift the container more? What is the GG’?

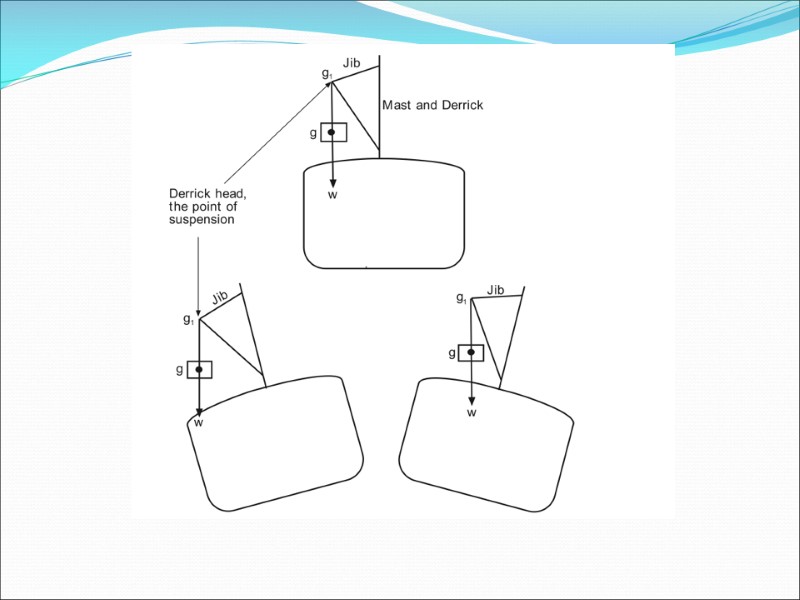
Principle of suspended weights When a weight is suspended by a ship’s derrick, its center of gravity is to be considered as being at the derrick head, and it will remain at the derrick head as long as the weight is suspended.
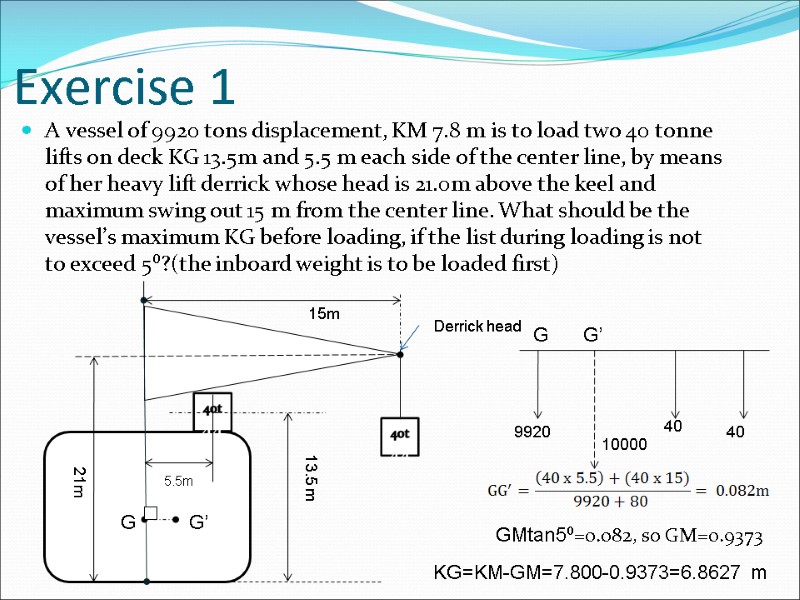
Exercise 1 A vessel of 9920 tons displacement, KM 7.8 m is to load two 40 tonne lifts on deck KG 13.5m and 5.5 m each side of the center line, by means of her heavy lift derrick whose head is 21.0m above the keel and maximum swing out 15 m from the center line. What should be the vessel’s maximum KG before loading, if the list during loading is not to exceed 5⁰?(the inboard weight is to be loaded first) 10000 40 GMtan5⁰=0.082, so GM=0.9373 KG=KM-GM=7.800-0.9373=6.8627 m

Basic rule about movement of G: When a weight is loaded on a vessel, G will directly toward the position of the loaded weight When a weight is discharge from a vessel, G will move directly away from the position of the discharged weight When a weight is suspended on a vessel, G will move toward the point of suspension. When a weight is shifted on a vessel, G will move parallel to the shifted weight.
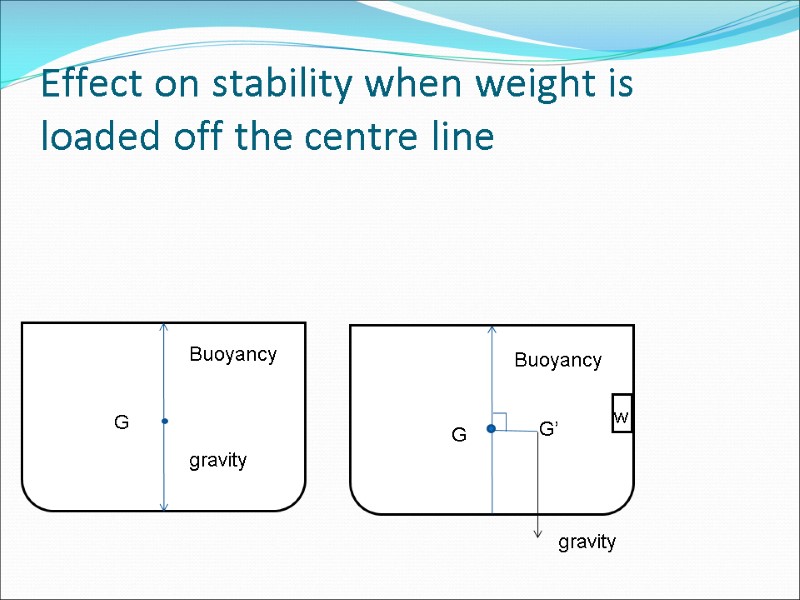
Effect on stability when weight is loaded off the centre line G G G’ w Buoyancy Buoyancy gravity gravity
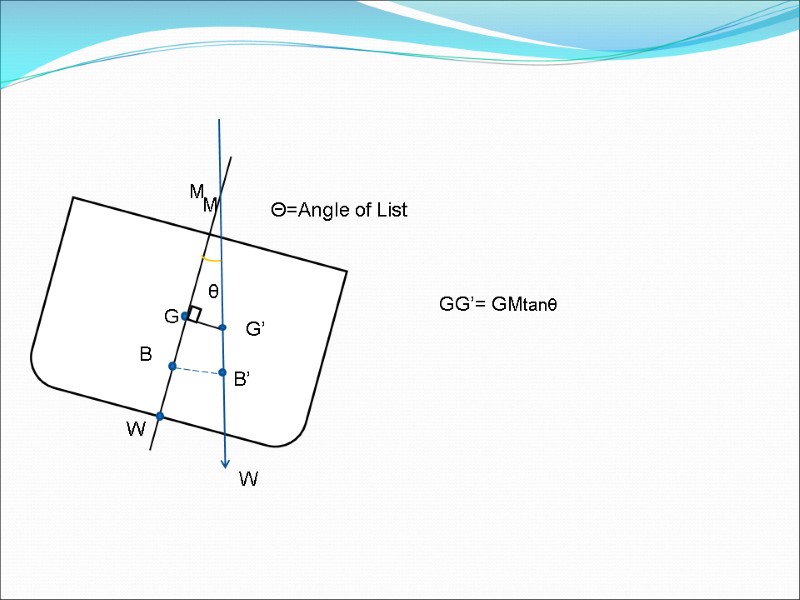
θ Θ=Angle of List M W W M B B’ G’ G GG’= GMtanθ

Example 6 A vessel of 6500 tons displacement has a KM 7.2 and KG 6.8m. A weight of 100 tons is shifted 2.3m to port and 3.9 m upwards if the vessel is initially upright, calculate the resulting list. For vertical shift GG’= (100 x 3.9)/6500 = 0.06 m rise For horizontal shift GG’= (100 x 2.3)/6500 = 0.0354 m to port KG=6.8m Then, KG’=6.86m KM= 7.20 m Then, G’M=+0.34 Tan θ =GG’/GM =0.0354/0.34 = 0.1041 Θ= 5.95⁰ to port

Steps to find KG Find KG for every cargo, fuel, water, and stores compartment or tank on the vessel Multiply these distances by the weights in the respective locations Add total weights including weight of light ship Add total moments including the moment of light ship Divide total moments by total weights produce final KG
7316-chapter_2_stability-new.ppt
- Количество слайдов: 43

