Ш Закон тождества в процессе определенного рассуждения всякое

Ш Закон тождества: в процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе. Ш Закон непротиворечия: невозможно чтолибо одновременно утверждать и отрицать. Сформулированы Аристотилем. Ш Закон исключения третьего: из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано. Ш Закон достаточного основания: всякая истинная мысль должна быть достаточно обоснована. Сформулирован Лейбницем

Доказать можно только истинные мысли, ложные доказать нельзя. «Ошибаться свойственно всякому человеку, но настаивать на ошибке свойственно только глупцу» . Только содержательный характер.

При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре высказываний производится на основе эквивалентных преобразований, опирающихся на основные логические законы. Законы алгебры высказываний (алгебры логики) – это тавтологии.

(содержат одну переменную) Закон тождества. Всякое понятие и суждение тождественно самому себе. А=А Закон тождества означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. При нарушении этого закона возможны логические ошибки. Движение вечно. Хождение в школу – движение. Следовательно, хождение в школу вечно.

Закон непротиворечия. A&A=1 A&A=0 Примеры: На Марсе есть жизнь и на Марсе жизни нет. Светлана окончила среднюю школу и учится в 10 классе. Закон исключения третьего. А / А = 1 Примеры: Число 12345 либо четное либо нечетное, третьего не дано. Ученик учится или хорошо или плохо. Эта жидкость является или не является кислотой.

Закон двойного отрицания. А=А А 0 1 А 1 0 А 0 1 А = Матроскин - кот А = Неверно, что Матроскин не кот

Свойства констант: 0=1 1=0 (отрицание лжи есть истина) (отрицание истины есть ложь) А / 0 = А А / 1 =1 А&0=0 А & 1 =A Законы идемпотентности А / А = А А&А=А (отсутствие коэффициентов) (отсутствие степеней)

Законы коммутативности А / В = В / А А&В=В&А Законы ассоциативности A /(B / C) = (A / B) / C A &(B & C) = (A & B) & C Законы дистрибутивности A /(B & C) = (A / B) & (A / C) (дистрибутивность дизъюнкции относительно конъюнкции) Доказать A &(B / C) = (A & B) / (A & C) (дистрибутивность конъюнкции относительно дизъюнкции)

Законы поглощения: А / (А & В) =A А & (А / В) =A Доказать

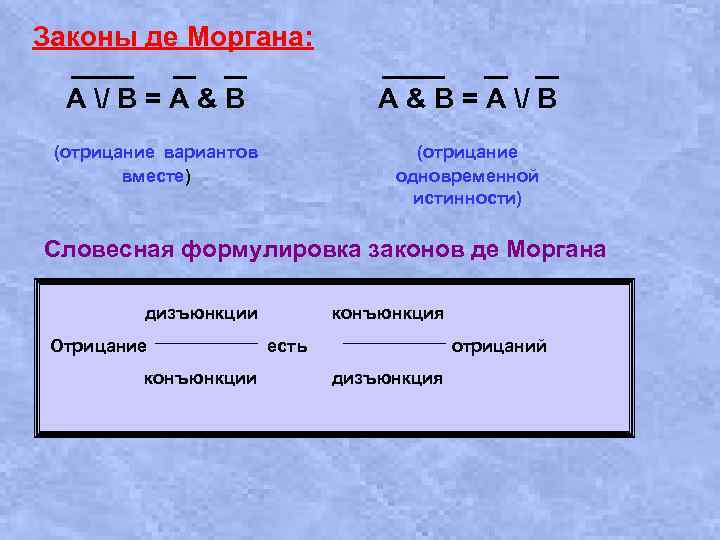Законы де Моргана: A / B = A & B = A / B (отрицание вариантов вместе) (отрицание одновременной истинности) Словесная формулировка законов де Моргана дизъюнкции Отрицание конъюнкции конъюнкция есть отрицаний дизъюнкция

Законы де Моргана: A / B = A & B = A / B (отрицание вариантов вместе) (отрицание одновременной истинности) Мнемоническое правило: в левой части тождества операция отрицания стоит над всем высказыванием. В правой она как бы разрывается и отрицание стоит над каждым из простых высказываний, но одновременно меняется операция: дизъюнкция на конъюнкцию и наоборот.

Высказывание Неверно, что я знаю арабский или китайский язык тождественно высказыванию Я не знаю арабского языка и не знаю китайского языка. Неверно, что я выучил урок и получил по нему двойку тождественно высказыванию Или я не выучил урок или я не получил по нему двойку.

Замена операции импликации и эквивалентности: A => B = A / B - замена импликации. A => B = A & B - замена импликации. Для замены операции эквивалентности существует два правила: A B = (A & B) / (A & B); A B = (A / B) & (A / B). Доказать!

Е = Неверно, что если я выиграю конкурс, то получу приз. А = Я выиграю конкурс В = Я получу приз. Е = A =>B = A / B = A & B Е = Я выиграю конкурс, но приз не получу.

Интерес представляют следующие правила: A => B => A A B = (A =>B) & (B => A) Фраза Если Винни-Пух съел мед, то он сыт тождественна фразе Если Винни-Пух не сыт, то меда он не ел.

Ш Аристотель Ш Готфрид Вильгельм Лейбниц Ш Огастес де Морган Ш Джордж Буль Ш Джордж Венн