СФЕРА Сферой называется поверхность состоящая из всех точек

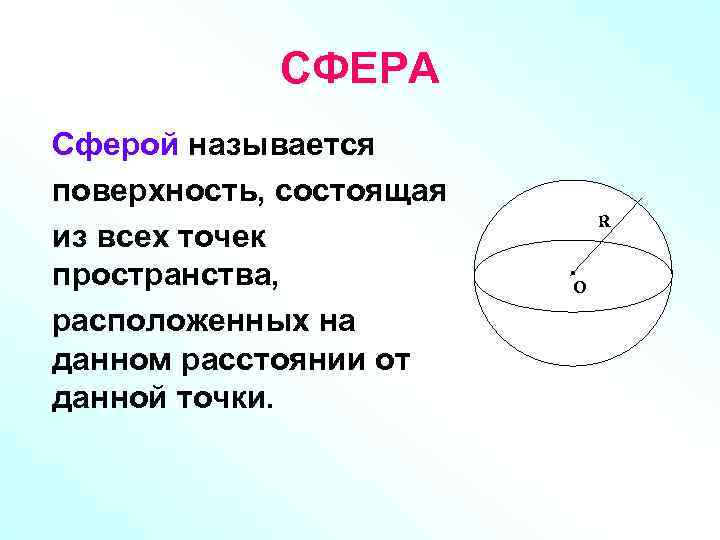СФЕРА Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. R O

Диаметр сферы Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. А D = 2 R С Сфера может быть получена вращением полуокружности вокруг её диаметра. В

Шар Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.

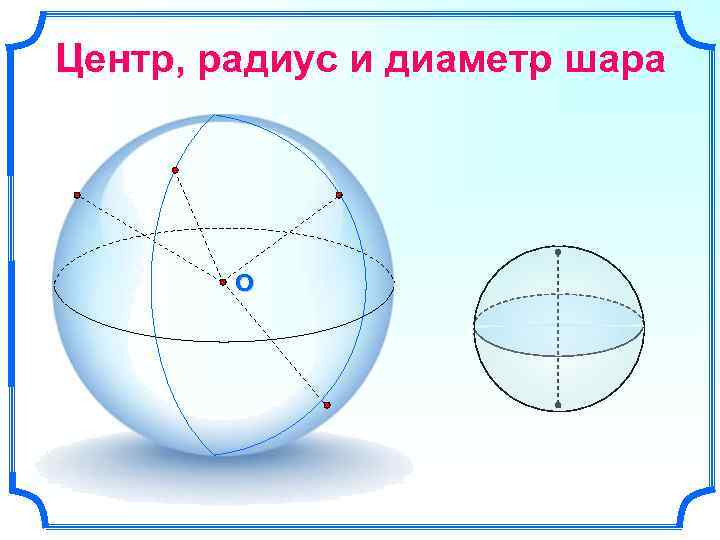Центр, радиус и диаметр шара O

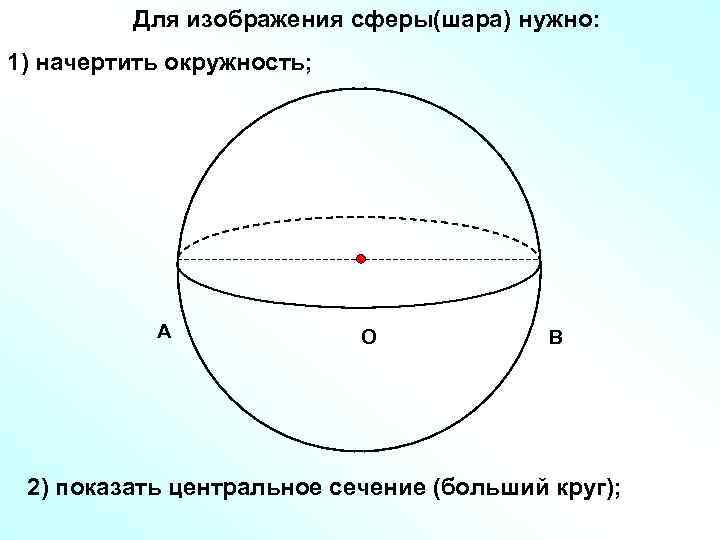Для изображения сферы(шара) нужно: 1) начертить окружность; A O B 2) показать центральное сечение (больший круг);

Шар или сфера?

Форму шара имеет не только Земля, но и другие планеты Солнечной системы и остальных галактик.

Арбуз и апельсин имеют почти идеальную форму шара.

Шарообразную форму могут иметь и цветы

Форму шара так же можно встретить и в животном мире

Уравнение сферы AB = (x 2–x 1)2+(y 2–y 1)2+(z 2–z 1)2 z I R I M(x; y; z) y I R CM = (x–x 0)2+(y–y 0)2+(z–z 0)2 I I I C(x 0; y 0; z 0) I x R 2 =(x–x 0)2+(y–y 0)2+(z–z 0)2

Центр r (x– 3)2 +(y– 2)2 +(z – 1)2=16 C(3; 2; 1) r=4 (x– 1)2+(y+2)2+(z+5)2 = 4 C(1; -2; -5) r=2 (x+5)2+(y– 3)2 + z 2 = 25 C(-5; 3; 0) C(1; 0; 0) r=5 r= 8 C(0; -2; -8) C(0; 0; 0) r= 2 r=3 Уравнение сферы (x – 1 )2 + y 2 + z 2 = 8 x 2 +(y+2)2 +(z+8)2 = 2 x 2 + y 2 + z 2= 9 (x– 3 )2+(y– 2)2 + z 2 = 0, 09 C(3; 2; 0) (x+7)2+(y– 5)2 +(z+1)2 = 2, 5 C(-7; 5; -1) 2 +(y+4)2 + (z+4)2 = 6 1 C(0; -4; 9) x 4 r = 0, 3 r = 2, 5 5 r= 2

Объём шара Площадь поверхности сферы

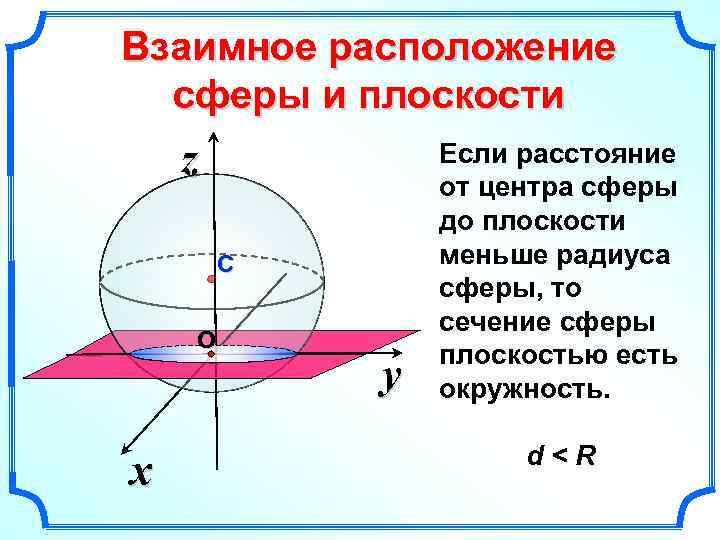Взаимное расположение сферы и плоскости z С О x y Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность. d

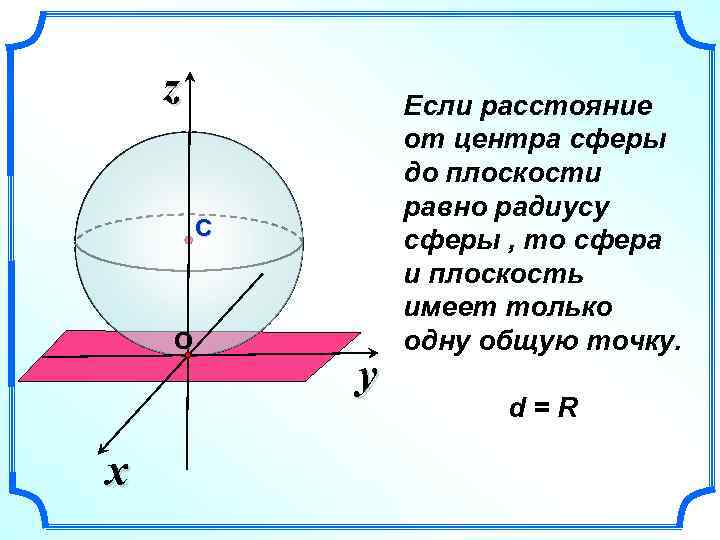z С О x y Если расстояние от центра сферы до плоскости равно радиусу сферы , то сфера и плоскость имеет только одну общую точку. d=R

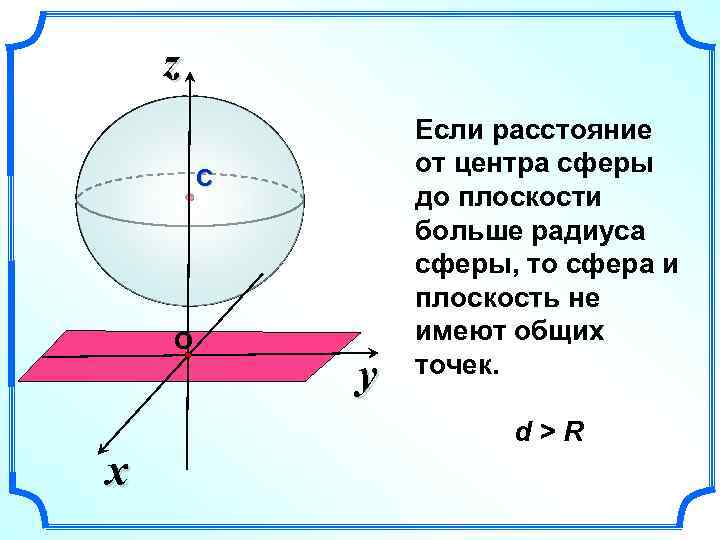z С О x y Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек. d>R

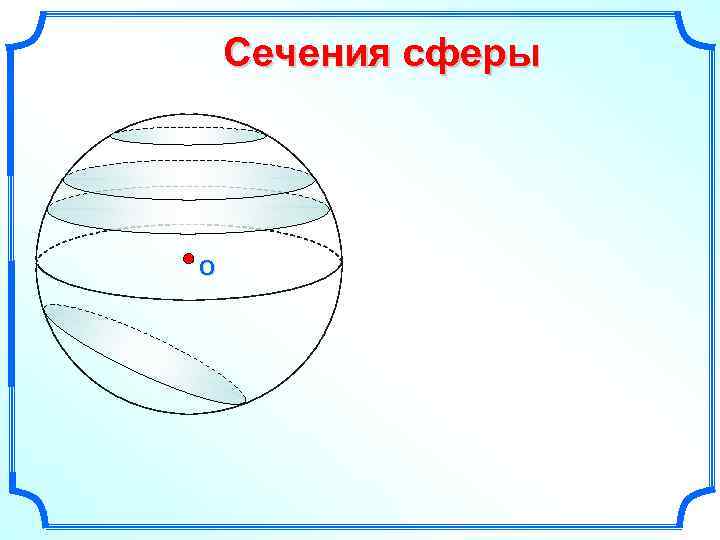Сечения сферы O

Сечения сферы

Части сферы и шара.

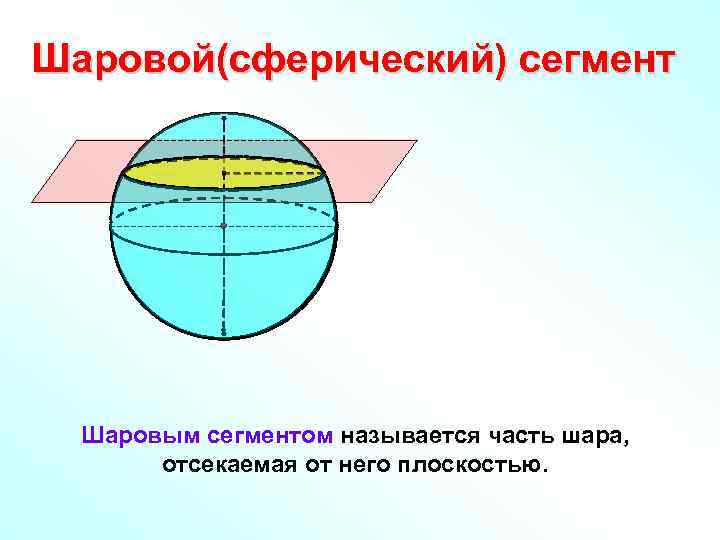Шаровой(сферический) сегмент Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.

Шаровой сегмент ограничен: 1) частью сферы, которая называется сегментной поверхностью; 2) кругом, который называется основанием шарового сегмента.

Радиус основания шарового сегмента (сегментной поверхности) Высота шарового сегмента (сегментной поверхности) Высотой шарового сегмента (сегментной поверхности) называется отрезок радиуса шара (сферы) перпендикулярного основанию сегмента, принадлежащий шаровому сегменту.

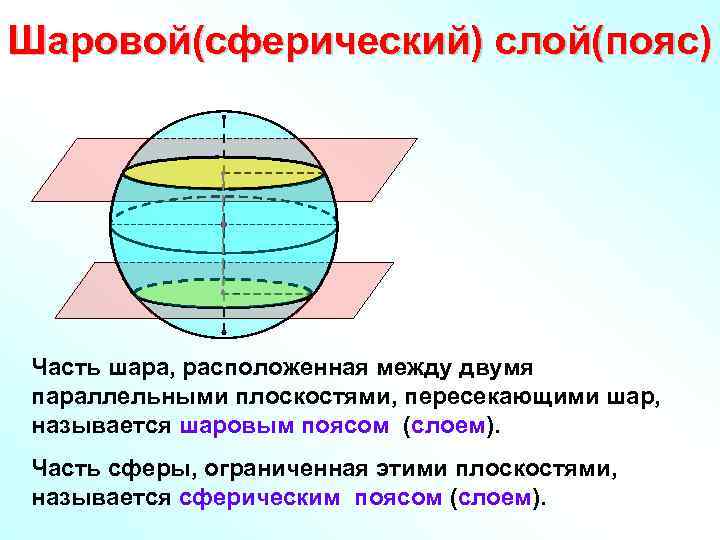Шаровой(сферический) слой(пояс) Часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар, называется шаровым поясом (слоем). Часть сферы, ограниченная этими плоскостями, называется сферическим поясом (слоем).

Поверхность шарового слоя состоит из двух кругов (оснований) и сферического пояса. Высотой шарового слоя называется отрезок диаметра сферы, перпендикулярного основаниям, заключенный между этими основаниями. Высотой сферического пояса называется высота соответствующего шарового слоя.

Шаровой сектор = Шаровой сегмент + конус.

Шаровым сектором называется фигура, полученная при вращении кругового сектора с острым углом вокруг прямой, содержащий один из ограничивающий сектор радиусов.

№ 573 Точки А и В лежат на сфере с центром О точка М лежит на отрезке АВ. Докажите, что а) если М – середина отрезка АВ, то OM б) если OM A АВ, а AB AB, то М – середина отрезка АВ. M O B A M O B

№ 574 Точка М – середина отрезка АВ, концы которого лежат сфере радиуса К с центром О. Найдите а) ОМ, если R=50 см, АВ=40 см. 40 A M ? O B 50

Планиметрия Стереометрия Свойство касательной. В А r О Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. А r О Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Планиметрия Стереометрия Признак касательной. А касательная В r О Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной. А касательная пл. r О Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательно к сфере.

№ 592 Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы. 15 А В N 112 О ВN – искомое расстояние

№ 584 Все стороны треугольника АВС касаются сферы радиуса 5 см. Найдите расстояние от центра сферы до плоскости треугольника, если АВ=13 см, ВС=14 см, СА=15 см. B М A O 1 N P C B O М A P N C

№ 585 Все стороны ромба, диагонали которого равны 15 см и 20 см, касаются сферы радиуса 10 см. Найдите расстояние о плоскости сферы до плоскости ромба. D M K O 1 A P C N B D O C A P N B

№ 591 Сфера касается граней двугранного угла в 1200. Найдите радиус сферы и расстояние между точками касания, если расстояние от центра сферы до ребра двугранного угла равно. a a

Повторение. Расположение центра описанной около треугольника окружности. Во внутренней области (для остроугольного треугольника) На середине гипотенузы (для прямоугольного P треугольника) М Во внешней области O (для тупоугольного треугольника) М O P N P O N М N

№ 581 Вершины треугольника АВС лежат на сфере радиуса 13 см. Найдите расстояние от центра сферы до плоскости треугольника, если АВ=6 см, ВС=8 см, АС=10 см. 102=82+62 А O 1 В С гипотен уза O А С O В

№ 582 Вершины прямоугольника АВСD лежат на сфере радиуса 10 см. Найдите расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16 см. 102=82+62 D А D O 1 С В O А O В С