СФЕРА Сферой наз поверхность состоящая из всех точек

СФЕРА Сферой наз. поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Данная точка называется центром сферы, а данное расстояние – радиусом сферы. Sсферы=4∏R 2

ШАР Тело, ограниченное сферой наз. шаром.

Диаметр сферы – отрезок соединяющий две точки сферы и проходящий через ее центр. Равен 2 R. Центр, радиус и диаметр шара соответственно равны и являются центром, радиусом и диаметром сферы.

УРАВНЕНИЕ СФЕРЫ Выведем уравнение сферы радиусом R с центром C(x 0, y 0, z 0). Поместим произвольную точку M(x, y, z) на сферу, тогда расстояние MC вычисляется по формуле МС = Так как MC лежит на сфере, MC = R, значит 2 2 2 R = (x-x 0) + (y-y 0) + (z-z 0) 2 В прямоугольной системе координат данное уравнение называется уравнением сферы с центром C(x 0, y 0, z 0) и радиусом R.

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ СФЕРЫ И ПЛОСКОСТИ Исследуем взаимное расположение сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от ее центра до плоскости. Радиус сферы обозначим буквой R, а расстояние от центра до плоскости буквой 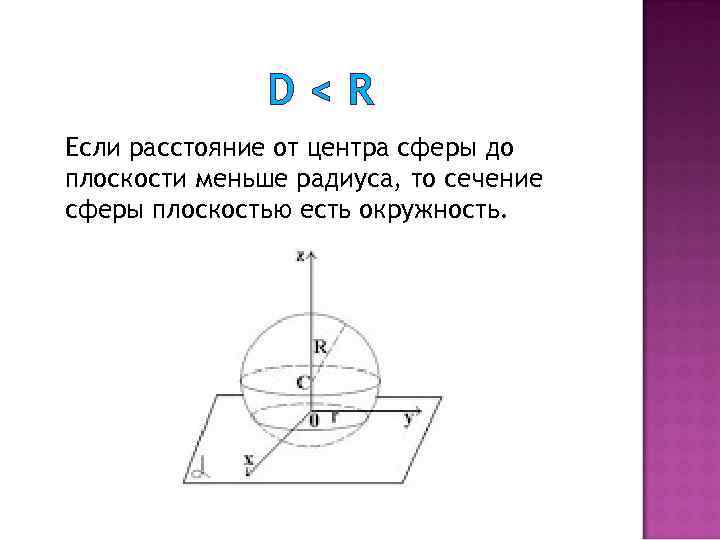D.

D

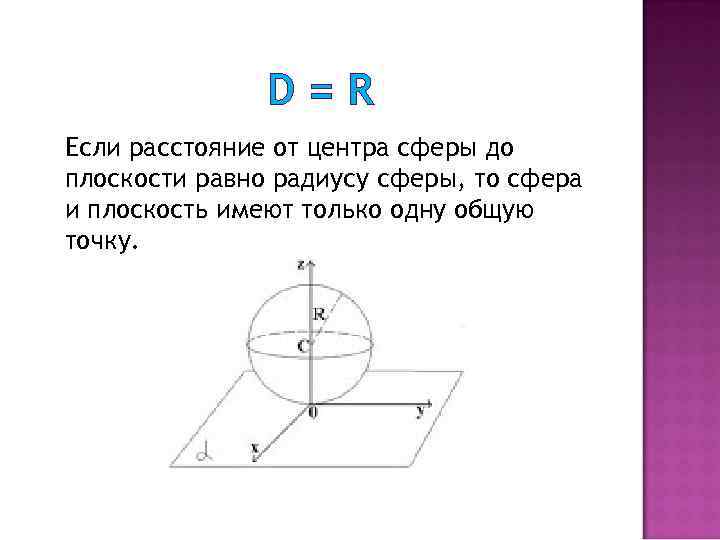D=R Если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку.

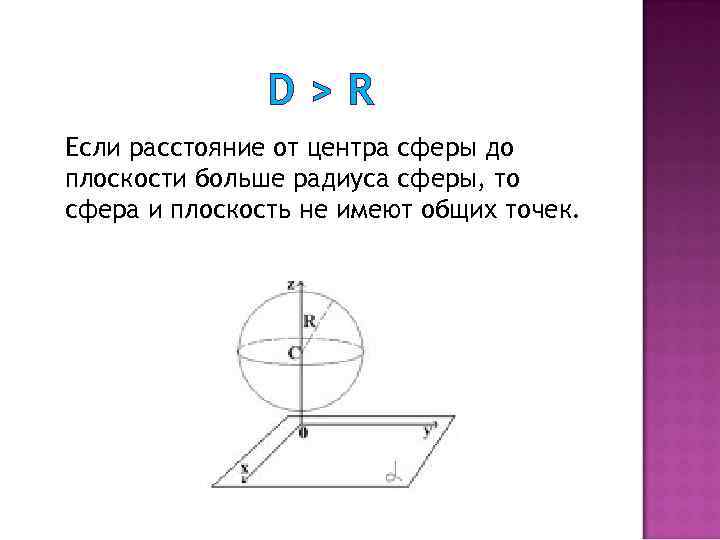D>R Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

КАСАТЕЛЬНАЯ ПЛОСКОСТЬ К СФЕРЕ Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере. Их общая точка называется точкой касания(А).

Теорема 1 Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. Теорема 2 Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.