Сезонная декомпозиция временного ряда v 3 План

Сезонная декомпозиция временного ряда v 3

План занятия • • Предварительный анализ временного ряда Сезонная декомпозиция временного ряда Расчет показателей ошибки прогноза Прогнозирование ex-post 2

Постановка задачи • В этом тренинге мы исследуем структуру временного ряда – оборот розничной торговли и выделим закономерные компоненты ряда • Будет использован метод стандартной декомпозиции временного ряда • Для выделения тренда будет использовано уравнение прямой линии • С помощью модели закономерных компонентов ряда мы построим прогноз на горизонте 12 месяцев • Для оценки качества модели будут рассчитаны показатели ошибки прогноза 3

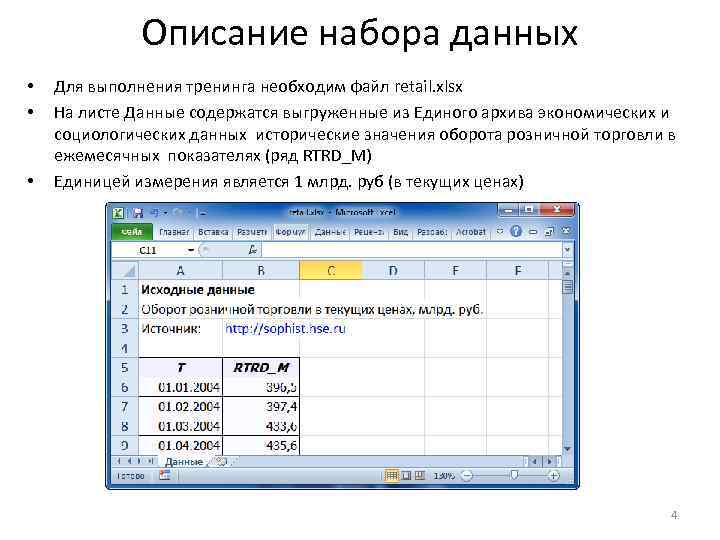Описание набора данных • • • Для выполнения тренинга необходим файл retail. xlsx На листе Данные содержатся выгруженные из Единого архива экономических и социологических данных исторические значения оборота розничной торговли в ежемесячных показателях (ряд RTRD_M) Единицей измерения является 1 млрд. руб (в текущих ценах) 4

Предварительный анализ данных • • • Установите курсор в таблицу и постройте (на отдельном листе) график изменения оборота во времени (команда Вставка>График на ленте) Добавьте на график линию линейного тренда (контекстное меню ряда данных) Ряд содержит очевидные закономерные компоненты: – Средний уровень ряда непрерывно растет (есть тренд) – Линейная модель тренда достаточно хорошо передает тенденцию в данных ряда – Хорошо различимы сезонные колебания продаж – пиковые продажи в декабре и спад продаж в январе каждого года, длительность сезонного цикла – 12 месяцев (год) – Амплитуда сезонных колебаний растет вместе со средним уровнем, тип сезонности - мультипликативная – Есть периоды (2006, 2008, 2010 г. ), когда средний уровень ряда систематически отклонялся от тренда в большую или меньшую сторону. Это может быть вызвано влиянием экономических циклов (кризис 20082009 г. ), либо неадекватностью выбранной модели тренда (нужна нелинейная модель) – За исключением влияния кризиса, отобранный исторический период не содержит заметных изменений 5 в закономерных компонентах ряда

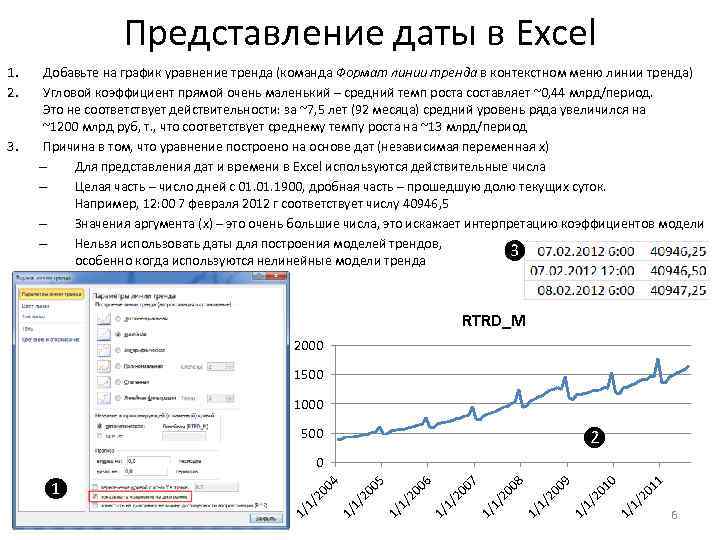Представление даты в Excel RTRD_M 2000 1500 1000 500 ❷ 1 01 1/ 1 /2 10 20 1/ 1/ 09 20 1/ 1/ /2 00 8 7 1/ 1 00 /2 1/ 1 /2 00 6 5 1/ 1 00 /2 1/ 1 00 ❶ 4 0 /2 3. Добавьте на график уравнение тренда (команда Формат линии тренда в контекстном меню линии тренда) Угловой коэффициент прямой очень маленький – средний темп роста составляет ~0, 44 млрд/период. Это не соответствует действительности: за ~7, 5 лет (92 месяца) средний уровень ряда увеличился на ~1200 млрд руб, т. , что соответствует среднему темпу роста на ~13 млрд/период Причина в том, что уравнение построено на основе дат (независимая переменная x) – Для представления дат и времени в Excel используются действительные числа – Целая часть – число дней с 01. 1900, дробная часть – прошедшую долю текущих суток. Например, 12: 00 7 февраля 2012 г соответствует числу 40946, 5 – Значения аргумента (x) – это очень большие числа, это искажает интерпретацию коэффициентов модели – Нельзя использовать даты для построения моделей трендов, ❸ особенно когда используются нелинейные модели тренда 1/ 1 1. 2. 6

Оценка коэффициентов тренда • • Для моделирования временного ряда необходимо строить тренд не по дате, а по номеру периода (1…N) Для оценки коэффициентов тренда удобно использовать функцию ЛИНЕЙН() – линейная регрессия – – Y b 1 = tg(a) b 0 Y = b 1 * X + b 0 Аргументами функции ЛИНЕЙН() являются диапазоны исходных данных – значения Y и X Если диапазон X не указан, то используются номера периодов 1. . N С помощью дополнительных параметров можно построить уравнение прямой, проходящей через начало координат (B 0 = 0), а также вывести статистики для оценки качества модели тренда Функция возвращает массив коэффициентов тренда – b 1 и b 0, поэтому необходимо вводить ее как формулу массива и заранее выделить диапазон ячеек, в который будут помещены коэффициенты 1. Добавьте на лист подписи в соответствии с рисунком и выделите диапазон из двух смежных ячеек (например, C 5: D 5) 2. Введите в строке формулу: = ЛИНЕЙН(укажите весь диапазон значений оборота) и нажмите CTRL-Shift-Enter (ввод формулы массива). Фигурные скобки в формуле добавляются автоматически и обозначают, что это формула массива. Их вводить не следует. ❶ ❷ 7 X

Моделирование тренда • Мы получили уравнение закономерного компонента ряда - тренда - с помощью функции ЛИНЕЙН(). Теперь, чтобы выделить второй закономерный компонент – сезонность, необходимо исключить тренд из данных. Для этого нам потребуются значения тренда (среднего уровня) ряда для каждого периода, которые можно рассчитать по уравнению тренда 1. Добавьте на лист столбец t, содержащий номер периода (1. . 92) – воспользуйтесь функцией автозаполнения 2. Добавьте для ячеек, содержащих значения коэффициентов тренда, имена: b_1 и b_0 3. Рассчитайте значения среднего уровня для каждого периода по уравнению тренда ( = b_0 + b_1 * номер текущего периода в столбце t) ❶ ❷ ❸ 8

Выделение сезонного компонента • На этапе предварительного анализа данных мы выяснили, что ряд имеет мультипликативную сезонность (амплитуда сезонных колебаний увеличивается с увеличением среднего уровня). Следовательно, для удаления тренда необходимо разделить исходные данные на значения тренда (для аддитивной сезонности тренд нужно вычитать) 1. 2. 3. ❶ Для удобства задайте имена диапазонов: • выделите все фактические значения и задайте для диапазона имя: Факт • аналогично, для диапазона значений тренда задайте имя: Тренд Добавьте на лист столбец Отношение, рассчитанный по формуле: = Факт / Тренд Хотя имена Факт и Тренд соответствуют диапазонам из нескольких значений, использование формулы Факт/Тренд корректно, т. к. Excel автоматически использует функцию неявного пересечения. Это означает, что операция деления выполняется не для всего диапазона, а только для текущей строки. Т. е. обрабатываются ячейки на пересечении диапазона и текущей строки. Задайте процентный формат для значений в столбце Отношение, поскольку сезонные коэффициенты характеризуют процентное отношение данного месяца к среднему уровню продаж ❷ ❸ 9

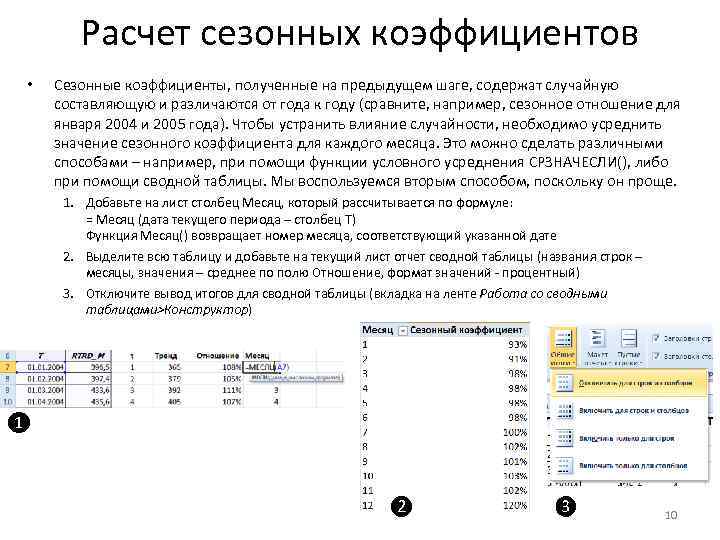Расчет сезонных коэффициентов • Сезонные коэффициенты, полученные на предыдущем шаге, содержат случайную составляющую и различаются от года к году (сравните, например, сезонное отношение для января 2004 и 2005 года). Чтобы устранить влияние случайности, необходимо усреднить значение сезонного коэффициента для каждого месяца. Это можно сделать различными способами – например, при помощи функции условного усреднения СРЗНАЧЕСЛИ(), либо при помощи сводной таблицы. Мы воспользуемся вторым способом, поскольку он проще. 1. Добавьте на лист столбец Месяц, который рассчитывается по формуле: = Месяц (дата текущего периода – столбец T) Функция Месяц() возвращает номер месяца, соответствующий указанной дате 2. Выделите всю таблицу и добавьте на текущий лист отчет сводной таблицы (названия строк – месяцы, значения – среднее по полю Отношение, формат значений - процентный) 3. Отключите вывод итогов для сводной таблицы (вкладка на ленте Работа со сводными таблицами>Конструктор) ❶ ❷ ❸ 10

Нормировка сезонных коэффициентов • Для сезонных коэффициентов должно выполняться условие нормировки: – при аддитивной сезонности – сумма сезонных коэффициентов = 0 – при мультипликативной сезонности – сумма сезонных коэффициентов = S (число периодов в одном сезонном цикле) • В данном случае это условие не выполняется (хотя ошибка небольшая) и необходимо нормировать коэффициенты 1. Рассчитайте сумму сезонных коэффициентов на основе данных сводной таблицы 2. Рассчитайте поправку ( = 12 / сумма сезонных коэффициентов ) 3. Рассчитайте нормированные сезонные коэффициенты ( = сезонный коэффициент * поправка ) Обратите внимание, что для расчета нормированного сезонного коэффициента используется обычная ссылка на ячейку: по умолчанию Excel подставляет функцию ПОЛУЧИТЬ. ДАННЫЕ. СВОДНОЙ. ТАБЛИЦЫ() ❸ ❶ ❷ 11

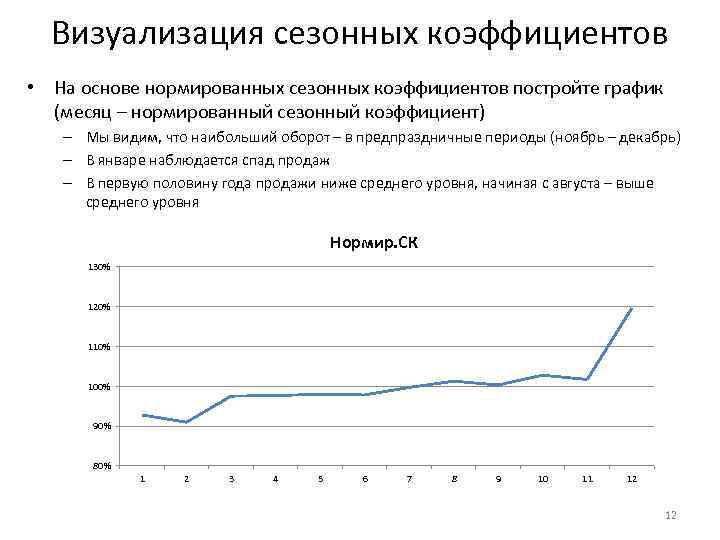Визуализация сезонных коэффициентов • На основе нормированных сезонных коэффициентов постройте график (месяц – нормированный сезонный коэффициент) – Мы видим, что наибольший оборот – в предпраздничные периоды (ноябрь – декабрь) – В январе наблюдается спад продаж – В первую половину года продажи ниже среднего уровня, начиная с августа – выше среднего уровня Нормир. СК 130% 120% 110% 100% 90% 80% 1 2 3 4 5 6 7 8 9 10 11 12 12

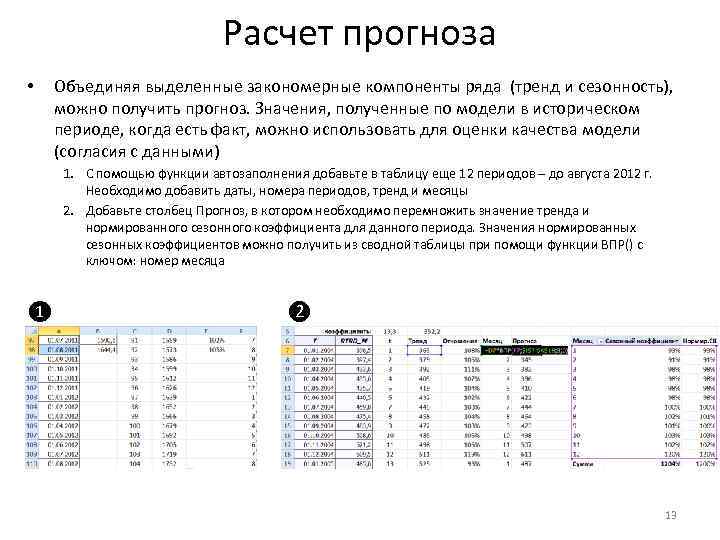Расчет прогноза • Объединяя выделенные закономерные компоненты ряда (тренд и сезонность), можно получить прогноз. Значения, полученные по модели в историческом периоде, когда есть факт, можно использовать для оценки качества модели (согласия с данными) 1. С помощью функции автозаполнения добавьте в таблицу еще 12 периодов – до августа 2012 г. Необходимо добавить даты, номера периодов, тренд и месяцы 2. Добавьте столбец Прогноз, в котором необходимо перемножить значение тренда и нормированного сезонного коэффициента для данного периода. Значения нормированных сезонных коэффициентов можно получить из сводной таблицы при помощи функции ВПР() с ключом: номер месяца ❶ ❷ 13

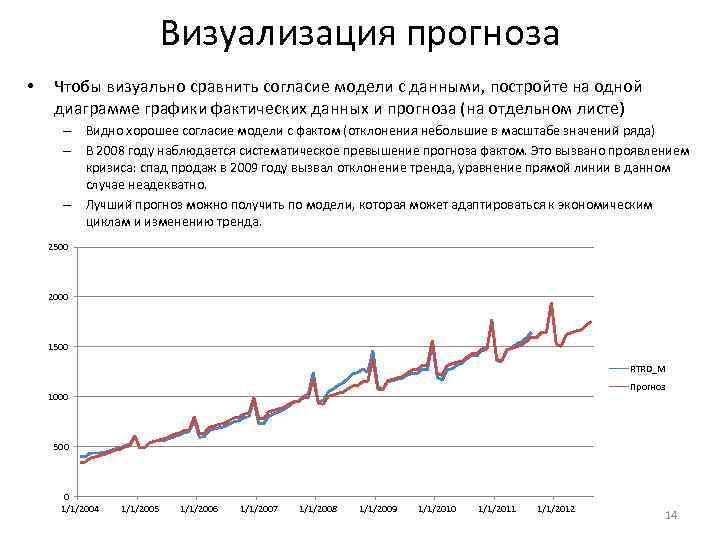Визуализация прогноза • Чтобы визуально сравнить согласие модели с данными, постройте на одной диаграмме графики фактических данных и прогноза (на отдельном листе) – Видно хорошее согласие модели с фактом (отклонения небольшие в масштабе значений ряда) – В 2008 году наблюдается систематическое превышение прогноза фактом. Это вызвано проявлением кризиса: спад продаж в 2009 году вызвал отклонение тренда, уравнение прямой линии в данном случае неадекватно. – Лучший прогноз можно получить по модели, которая может адаптироваться к экономическим циклам и изменению тренда. 2500 2000 1500 RTRD_M Прогноз 1000 500 0 1/1/2004 1/1/2005 1/1/2006 1/1/2007 1/1/2008 1/1/2009 1/1/2010 1/1/2011 1/1/2012 14

Расчет показателей ошибки • Показатели ошибки прогноза возможно рассчитать для исторического периода, когда доступны фактические данные – для расчета используются известные фактические значения и значения, которые получены с помощью применяемой модели прогнозирования в историческом периоде – модель, которая дает меньшую ошибку на историческом периоде, вероятно, будет работать хорошо и прогнозе на будущее – учитывая проблему переобучения модели, а также то, что статистический прогноз всегда основан на предположении о том, что закономерности изменения ряда в будущем останутся неизменными, малая ошибка на историческом периоде не гарантирует точность прогноза на будущее • Для качества модели сезонной декомпозиции: – рассчитаем абсолютные и относительные показатели ошибки – применим метод ex-post (пост-прогноз) 15

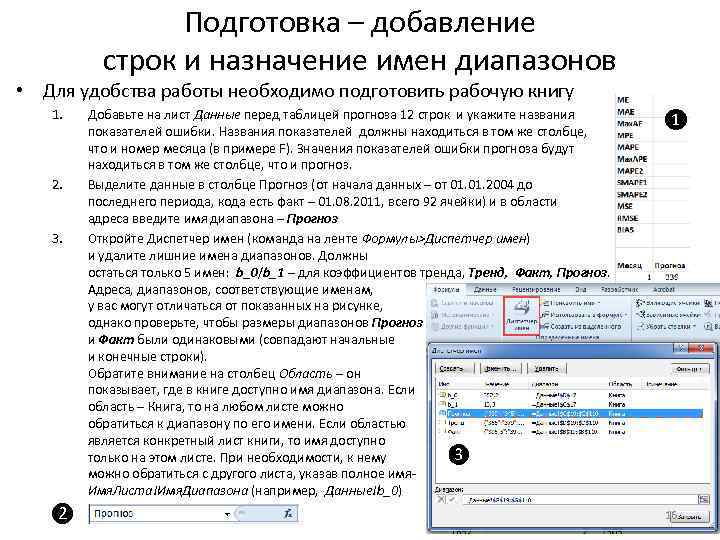Подготовка – добавление строк и назначение имен диапазонов • Для удобства работы необходимо подготовить рабочую книгу 1. 2. 3. ❷ Добавьте на лист Данные перед таблицей прогноза 12 строк и укажите названия показателей ошибки. Названия показателей должны находиться в том же столбце, что и номер месяца (в примере F). Значения показателей ошибки прогноза будут находиться в том же столбце, что и прогноз. Выделите данные в столбце Прогноз (от начала данных – от 01. 2004 до последнего периода, кода есть факт – 01. 08. 2011, всего 92 ячейки) и в области адреса введите имя диапазона – Прогноз Откройте Диспетчер имен (команда на ленте Формулы>Диспетчер имен) и удалите лишние имена диапазонов. Должны остаться только 5 имен: b_0/b_1 – для коэффициентов тренда, Тренд, Факт, Прогноз. Адреса, диапазонов, соответствующие именам, у вас могут отличаться от показанных на рисунке, однако проверьте, чтобы размеры диапазонов Прогноз и Факт были одинаковыми (совпадают начальные и конечные строки). Обратите внимание на столбец Область – он показывает, где в книге доступно имя диапазона. Если область – Книга, то на любом листе можно обратиться к диапазону по его имени. Если областью является конкретный лист книги, то имя доступно ❸ только на этом листе. При необходимости, к нему можно обратиться с другого листа, указав полное имя. Имя. Листа!Имя. Диапазона (например, Данные!b_0) ❶ 16

Вычисление средней ошибки • Для вычисления средней ошибки необходимо в каждом периоде вычислить остаток (ошибку модели) и затем полученные остатки усреднить. Однако мы не будем использовать для расчета остатков отдельный столбец и вместо этого используем более компактный способ, основанный на использовании формул массивов. В книге уже определены имена диапазонов, которые необходимо обработать – Факт и Прогноз ❶ 1. В ячейке справа от названия показателя ME (Mean Error/средняя ошибка) введите формулу массива: =СРЗНАЧ(Фaкт-Прогнoз). 2. Для завершения ввода формул массива необходимо использовать сочетание клавиш: Ctrl-Enter. В строке формул вокруг формулы ❷ автоматически отображаются фигурные скобки. Специально их вводить не нужно. 3. Формула массива обозначает, что действие, заданное формулой (в данном случае – разность значений в столбцах Факт и Прогноз) ❸ должно выполняться поэлементно – для каждой строки в диапазонах Факт и Прогноз. Результатом является массив значений остатков модели (он на листе не отображается). Затем мы при помощи функции СРЗНАЧ() вычисляем среднее значение по этому массиву, т. е. среднюю ошибку. Если вы введете формулу как обычную – по Enter, то будет выведено сообщение об ошибке #ЗНАЧ, т. к. операция «разность» определена только для двух значений. Эту операцию нельзя применять одновременно для множества ячеек. Формулы массива очень удобно использовать для расчета показателей ошибки, поскольку рабочий лист не загромождается промежуточными вычислениями (остатки, модули, квадраты) 17

Вычисление средней и максимальной абсолютной ошибки • • Средняя ошибка (ME) характеризует наличие смещения (систематической ошибки) в прогнозе. У хорошей модели смещения нет, поэтому положительные и отрицательные ошибки в разных периодах компенсируют друга и показатель ME близок к 0. Для того, чтобы оценить, насколько хорошо фактические значения ложатся на линию прогноза, необходимо использовать показатели, в которых остатки заменяются на их модули или квадраты (для исключения отрицательных остатков). 1. 2. Поведение прогноза в целом можно оценить при помощи показателя «Средняя абсолютная ошибка» (Mean Absolute Error, MAE). Для расчета этого показателя используйте формулу : ❶ =СРЗНAЧ(Abs(Фaкт-Прогнoз)) (формулу нужно вводить как формулу массива). ❷ Этот показатель характеризует, насколько далеко, в среднем, находится фактическое значение от линии прогноза. Максимальное отклонение факта от прогноза можно оценить при помощи показателя Max. AE (Maximum Absolute Error, Max. AE). Соответственно, используется формула: =МАКC(Фaкт-Прогнoз) 18

Вычисление относительных показателей ошибки • Абсолютные показатели ошибки имеют простую интерпретацию, но их сложно использовать для сравнения различных временных рядов, т. к. величина средней ошибки зависит от порядка изучаемой величины. Для устранения этой проблемы используются относительные показатели, которые выражают величину ошибки в процентах от фактического значения 1. Средняя процентная ошибка (Mean Percent Error, MPE) характеризует относительное смещение прогноза и вычисляется как средний относительный остаток (=СРЗНАЧ((Факт-Прогноз)/Факт)). ❶ В данном случае, смещения нет: MPE = 0. 1% ❷ 2. Средняя абсолютная ошибка в процентах (Mean Absolute Percent Error/MAPE) характеризует среднее отклонение факта от прогноза, ❸ выраженное в процентах от фактических значений: (=СРЗНAЧ(Abs(Фaкт-Прогнoз)/Фaкт)) MAPE – наиболее часто используемый на практике показатель ошибки прогноза. Иногда для удобства интерпретации неспециалистами и представления результатов руководству применяется «позитивный» показатель: «Точность прогноза» = 100%-MAPE. Однако поскольку MAPE вполне может быть и больше 100%, «точность» может оказаться отрицательной… 3. Максимальная абсолютная ошибка в процентах (Max. APE) характеризует максимальное относительное отклонение факта от прогноза. Для вычисления замените функцию СРЗНАЧ() на МАКС(). 19

Вычисление относительных показателей ошибки по альтернативным формулам • Для прерывистых временных рядов (есть периоды с нулевыми значениями) относительные показатели ошибки вычислить невозможно из-за деления на 0 в тех периодах, где Факт = 0. Чтобы исключить эту проблему, применяются альтернативные формулы, которые уменьшают вероятность деления на 0 1. В модифицированном MAPE (MAPE 2) вместо того, чтобы усреднять модули относительных остатков по всем периодам, вычисляется отношение суммы модулей остатков к сумме модулей фактических значений: = СУММ(Abs(Факт-Прoгноз))/СУММ(Фaкт) ❶ Поскольку хотя бы в одном периоде гарантированно ❷ должны быть положительные значения, деление на 0 при расчете по такой формуле исключено. Результат будет отличаться от значения, ❸ полученного по «стандартной» формуле, их нельзя между собой сравнивать. 2. «Симметричный» MAPE (Symmetric MAPE, SMAPE) также позволяет снизить вероятность деления на 0, поскольку если либо факт, либо прогноз в периоде будут положительными, то знаменатель будет отличаться от нуля. Применяются две модификации SMAPE: • в знаменателе – среднее между фактом и прогнозом на период: =CРЗНАЧ(Abs(Фaкт-Прогноз)/(СРЗНАЧ (Факт; Прoгноз)) • в знаменателе – максимум из факта и прогноза на период: =CРЗНАЧ(Abs(Фaкт-Прoгноз)/(МАКC (Факт; Прoгноз)) При использовании модифицированных показателей (SMAPE) величина ошибки также отличается от MAPE и будет несколько ниже, т. к. знаменатели при расчете относительных остатков больше (берется либо максимум из факта и прогноза, либо среднее). 20

Вычисление специальных абсолютных показателей ошибки • Специальные показатели – средний квадрат ошибки (Mean Squared Error, MSE) и стандартная ошибка (Root Mean Squared Error, RMSE) используются для статистического анализа ошибок модели. RMSE – более удобный показатель, т. к. он измеряется в тех же единицах, что и прогнозируемая величина. 1. Средний квадрат ошибки можно рассчитать по формуле: =СРЗНAЧ((Факт-Прогнoз)^2) На основе минимизации MSE выполняется подбор оптимальных коэффициентов модели прогнозирования. Преимущество перед функцией «Модуль» в том, что для функции «квадрат» можно аналитически найти минимум (с помощью достаточного условия экстремума). Именно на этом принципе основан «Метод наименьших квадратов» . 2. Стандартная ошибка позволяет оценить степень неопределенности прогноза и построить доверительный интервал. Примерно 95% ошибок прогноза находятся в интервале: +/- 2 * RMSE. В логистике стандартную ошибку прогноза или границы доверительного интервала для прогноза можно использовать для расчета страхового запаса. Стандартная ошибка – это квадратный корень из MSE. (в Excel используйте функцию КОРЕНЬ()) ❶ ❷ 21

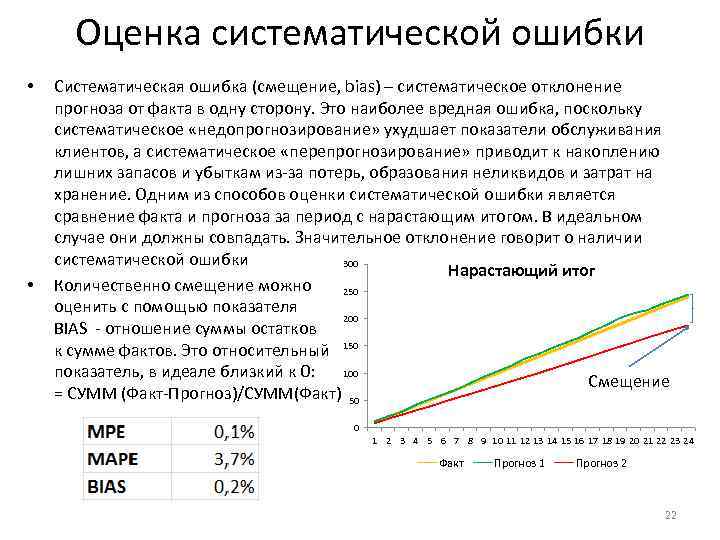Оценка систематической ошибки • • Систематическая ошибка (смещение, bias) – систематическое отклонение прогноза от факта в одну сторону. Это наиболее вредная ошибка, поскольку систематическое «недопрогнозирование» ухудшает показатели обслуживания клиентов, а систематическое «перепрогнозирование» приводит к накоплению лишних запасов и убыткам из-за потерь, образования неликвидов и затрат на хранение. Одним из способов оценки систематической ошибки является сравнение факта и прогноза за период с нарастающим итогом. В идеальном случае они должны совпадать. Значительное отклонение говорит о наличии систематической ошибки 300 Нарастающий итог Количественно смещение можно 250 оценить с помощью показателя 200 BIAS - отношение суммы остатков к сумме фактов. Это относительный 150 100 показатель, в идеале близкий к 0: Смещение = СУMM (Фaкт-Прогноз)/СУММ(Фaкт) 50 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Факт Прогноз 1 Прогноз 2 22

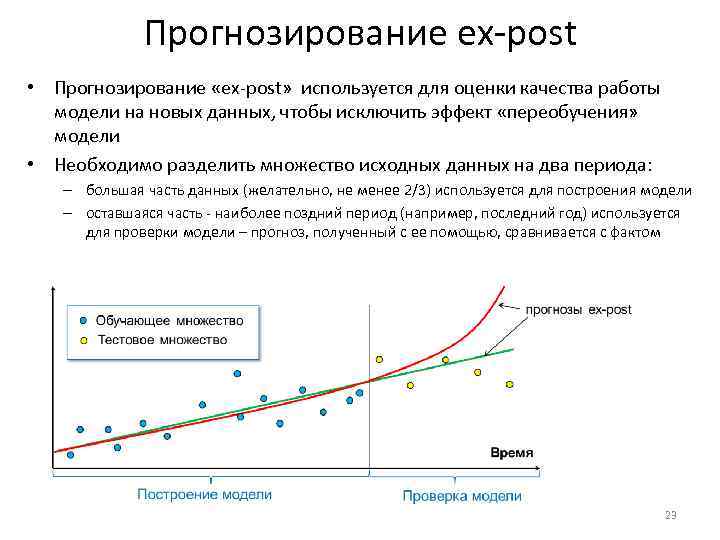Прогнозирование ex-post • Прогнозирование «ex-post» используется для оценки качества работы модели на новых данных, чтобы исключить эффект «переобучения» модели • Необходимо разделить множество исходных данных на два периода: – большая часть данных (желательно, не менее 2/3) используется для построения модели – оставшаяся часть - наиболее поздний период (например, последний год) используется для проверки модели – прогноз, полученный с ее помощью, сравнивается с фактом 23

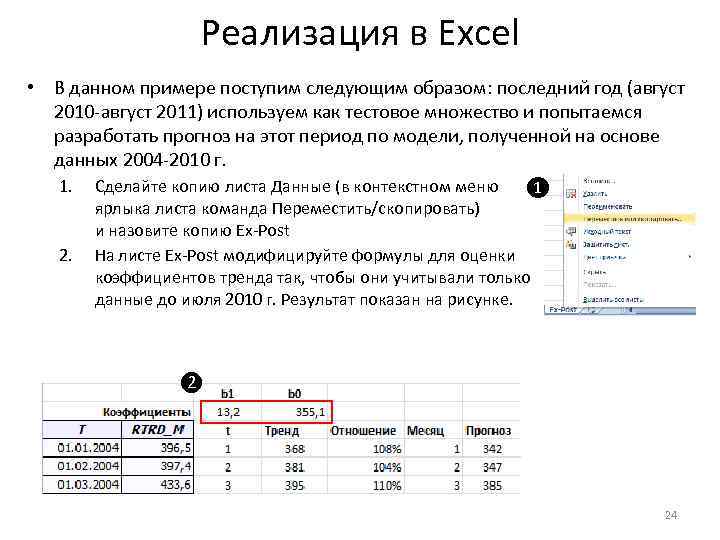Реализация в Excel • В данном примере поступим следующим образом: последний год (август 2010 -август 2011) используем как тестовое множество и попытаемся разработать прогноз на этот период по модели, полученной на основе данных 2004 -2010 г. 1. 2. Сделайте копию листа Данные (в контекстном меню ❶ ярлыка листа команда Переместить/скопировать) и назовите копию Ex-Post На листе Ex-Post модифицируйте формулы для оценки коэффициентов тренда так, чтобы они учитывали только данные до июля 2010 г. Результат показан на рисунке. ❷ 24

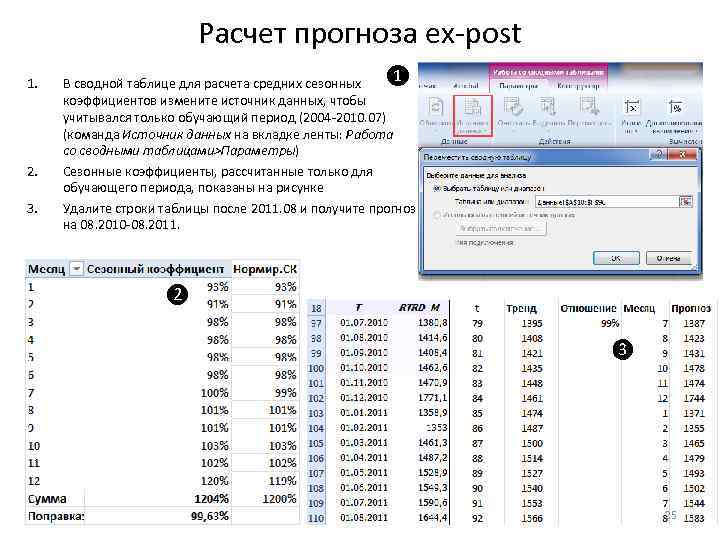Расчет прогноза ex-post 1. 2. 3. ❶ В сводной таблице для расчета средних сезонных коэффициентов измените источник данных, чтобы учитывался только обучающий период (2004 -2010. 07) (команда Источник данных на вкладке ленты: Работа со сводными таблицами>Параметры) Сезонные коэффициенты, рассчитанные только для обучающего периода, показаны на рисунке Удалите строки таблицы после 2011. 08 и получите прогноз на 08. 2010 -08. 2011. ❷ ❸ 25

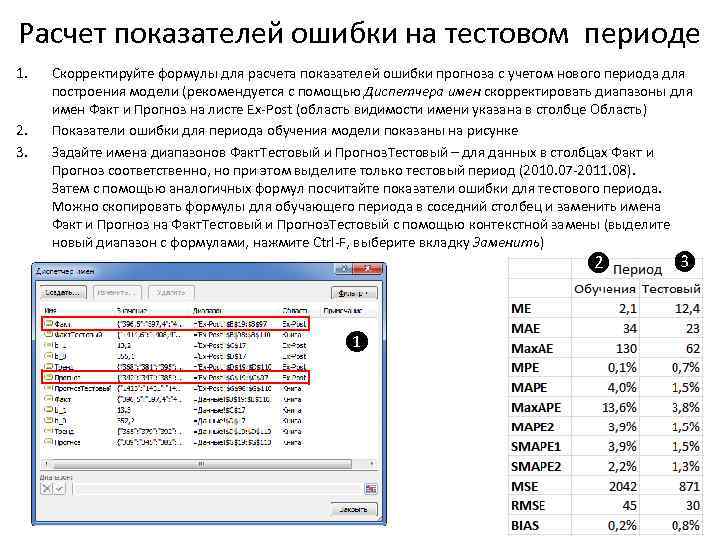Расчет показателей ошибки на тестовом периоде 1. 2. 3. Скорректируйте формулы для расчета показателей ошибки прогноза с учетом нового периода для построения модели (рекомендуется с помощью Диспетчера имен скорректировать диапазоны для имен Факт и Прогноз на листе Ex-Post (область видимости имени указана в столбце Область) Показатели ошибки для периода обучения модели показаны на рисунке Задайте имена диапазонов Факт. Тестовый и Прогноз. Тестовый – для данных в столбцах Факт и Прогноз соответственно, но при этом выделите только тестовый период (2010. 07 -2011. 08). Затем с помощью аналогичных формул посчитайте показатели ошибки для тестового периода. Можно скопировать формулы для обучающего периода в соседний столбец и заменить имена Факт и Прогноз на Факт. Тестовый и Прогноз. Тестовый с помощью контекстной замены (выделите новый диапазон с формулами, нажмите Ctrl-F, выберите вкладку Заменить) ❷ ❸ ❶ 26

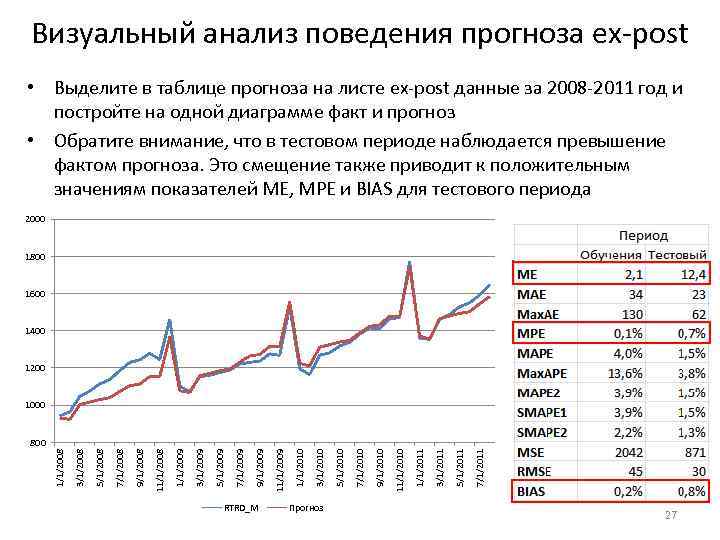Визуальный анализ поведения прогноза ex-post • Выделите в таблице прогноза на листе ex-post данные за 2008 -2011 год и постройте на одной диаграмме факт и прогноз • Обратите внимание, что в тестовом периоде наблюдается превышение фактом прогноза. Это смещение также приводит к положительным значениям показателей ME, MPE и BIAS для тестового периода 2000 1800 1600 1400 1200 1000 RTRD_M Прогноз 7/1/2011 5/1/2011 3/1/2011 11/1/2010 9/1/2010 7/1/2010 5/1/2010 3/1/2010 11/1/2009 9/1/2009 7/1/2009 5/1/2009 3/1/2009 11/1/2008 9/1/2008 7/1/2008 5/1/2008 3/1/2008 1/1/2008 800 27