5f730345d895cd00b4eac0972eb64085.ppt
- Количество слайдов: 43

Setting up an Initial CF Model Eberhard O. Voit September 1, 2011

Note: FDA just released strategic plan (August 17, 2011) “Advancing Regulatory Science at the FDA” Priority area # 1: Modernize Toxicology to Enhance Product Safety · Evaluate and develop models better able to predict patient response. · Identify improved biomarkers to monitor toxicity levels. · Integrate computational tools to inform conclusions about preclinical data.
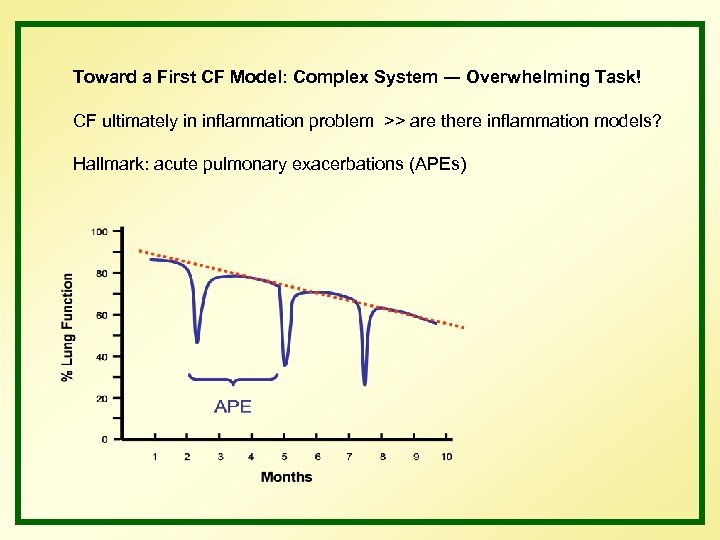
Toward a First CF Model: Complex System ― Overwhelming Task! CF ultimately in inflammation problem >> are there inflammation models? Hallmark: acute pulmonary exacerbations (APEs)
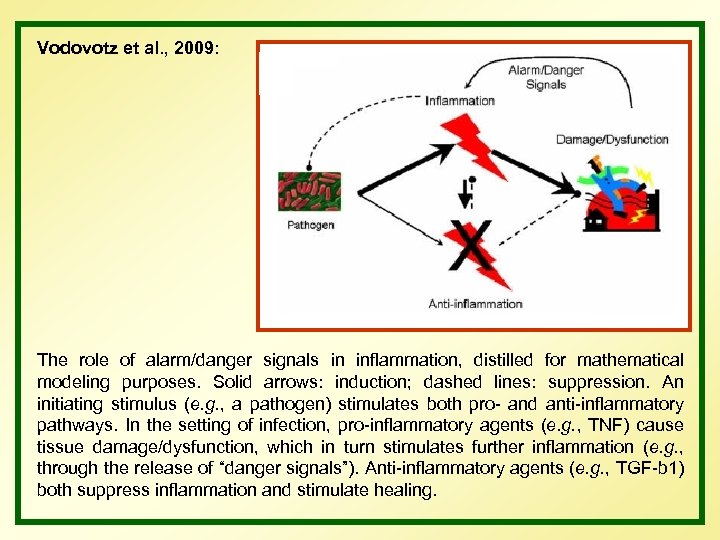
Vodovotz et al. , 2009: The role of alarm/danger signals in inflammation, distilled for mathematical modeling purposes. Solid arrows: induction; dashed lines: suppression. An initiating stimulus (e. g. , a pathogen) stimulates both pro- and anti-inflammatory pathways. In the setting of infection, pro-inflammatory agents (e. g. , TNF) cause tissue damage/dysfunction, which in turn stimulates further inflammation (e. g. , through the release of “danger signals”). Anti-inflammatory agents (e. g. , TGF-b 1) both suppress inflammation and stimulate healing.
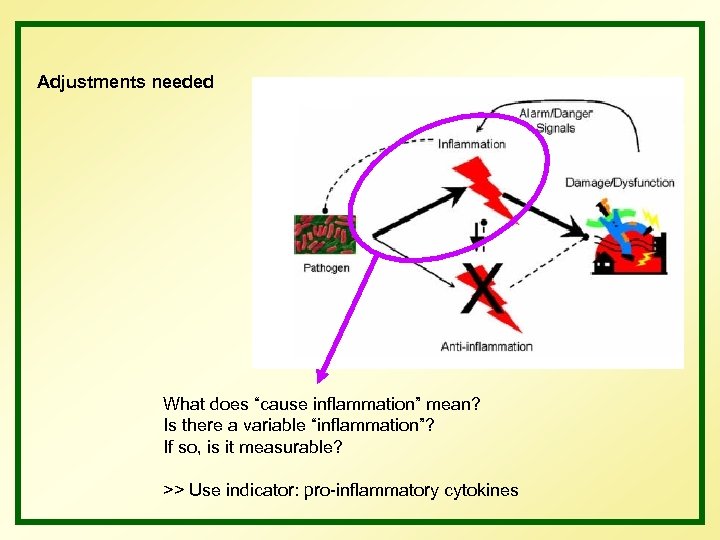
Adjustments needed What does “cause inflammation” mean? Is there a variable “inflammation”? If so, is it measurable? >> Use indicator: pro-inflammatory cytokines
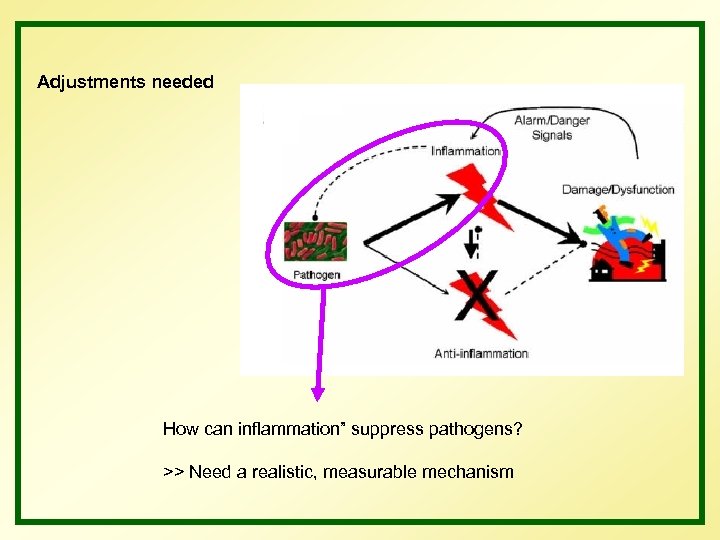
Adjustments needed How can inflammation” suppress pathogens? >> Need a realistic, measurable mechanism
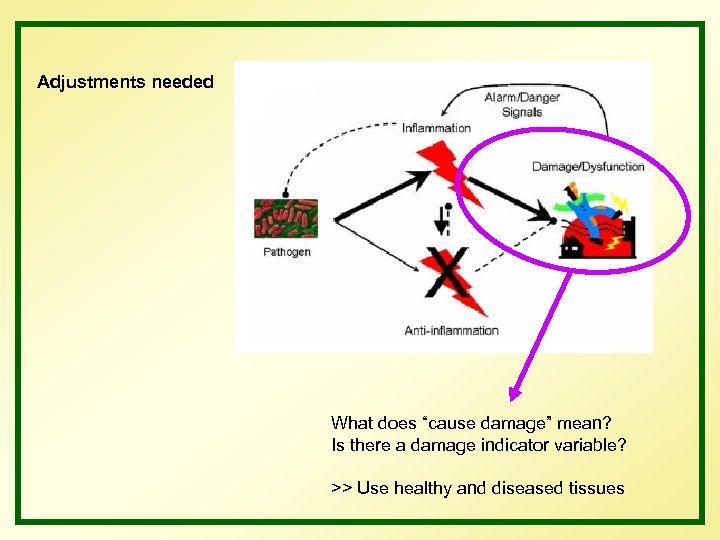
Adjustments needed What does “cause damage” mean? Is there a damage indicator variable? >> Use healthy and diseased tissues
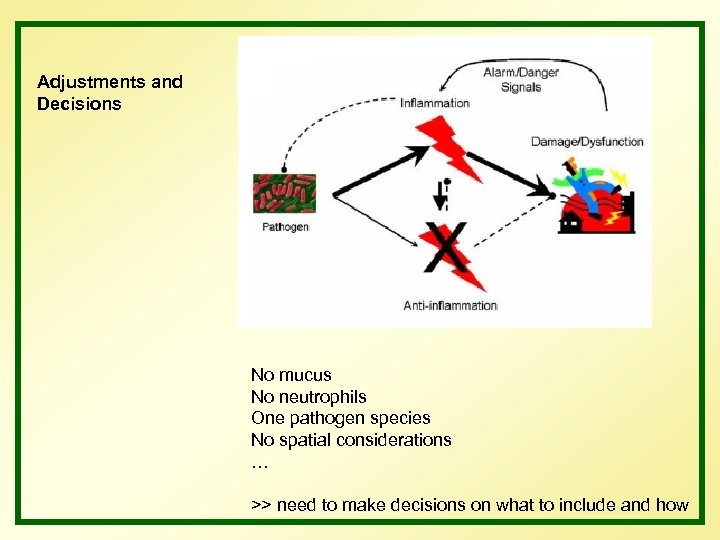
Adjustments and Decisions No mucus No neutrophils One pathogen species No spatial considerations … >> need to make decisions on what to include and how

Players Healthy Tissue Damaged Tissue Mucus Bacteria Anti-inflammatory Cytokines Pro-inflammatory Cytokines Need to model the role of CF >> Do I need to model the mutation? Missing transporter?
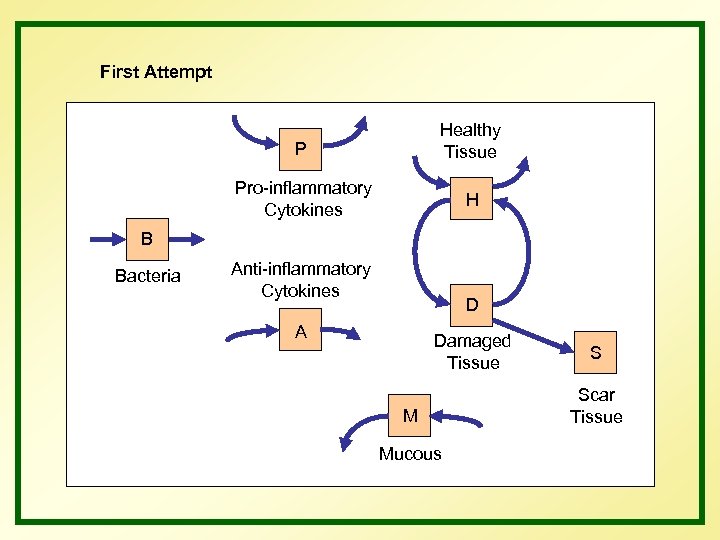
First Attempt P Healthy Tissue Pro-inflammatory Cytokines H B Bacteria Anti-inflammatory Cytokines D A Damaged Tissue M Mucous S Scar Tissue
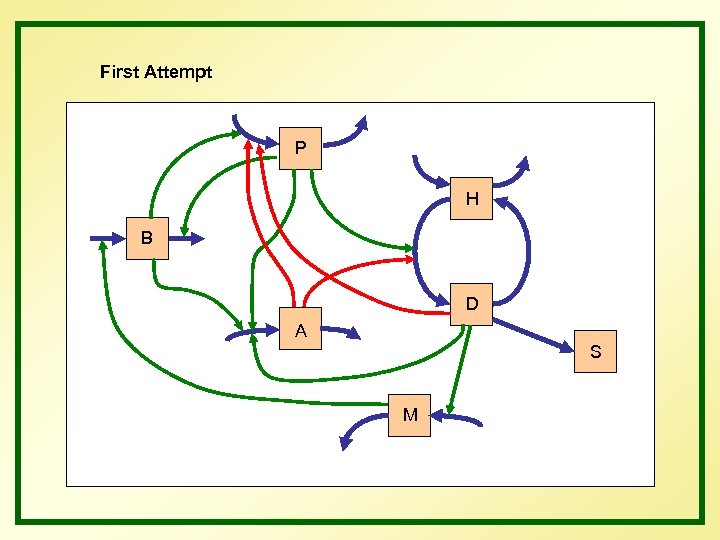
First Attempt P H B D A S M
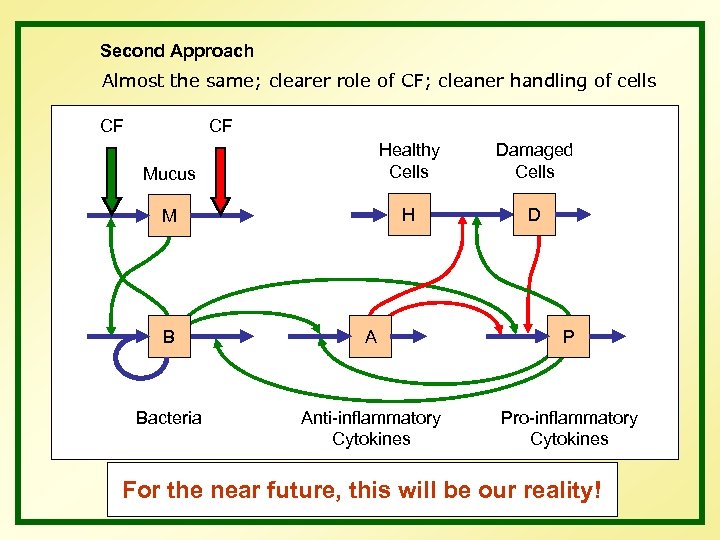
Second Approach Almost the same; clearer role of CF; cleaner handling of cells CF CF Mucus Healthy Cells Damaged Cells M H D B A P Bacteria Anti-inflammatory Cytokines Pro-inflammatory Cytokines For the near future, this will be our reality!
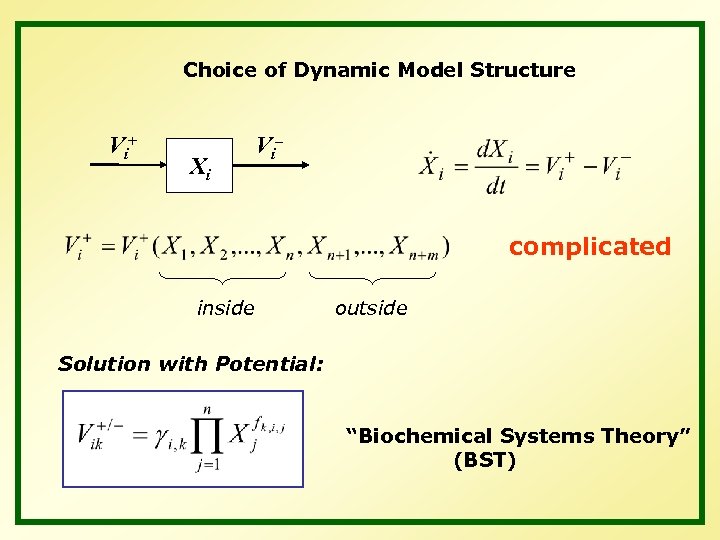
Choice of Dynamic Model Structure V i+ Xi V i– complicated inside outside Solution with Potential: “Biochemical Systems Theory” (BST)

Advantages of BST Models Prescribed model design: Rules for translating diagrams into equations; rules can be automated Direct interpretability of parameters and other features One-to-one relationship between parameters and model structure simplifies parameter estimation and model identification Simplified steady-state computations (for S-systems), including steady-state equations, stability, sensitivities, gains Simplified optimization under steady-state conditions Efficient numerical solutions and time-dependent sensitivities Minimal bias of model choice and minimal model size; easy scalability
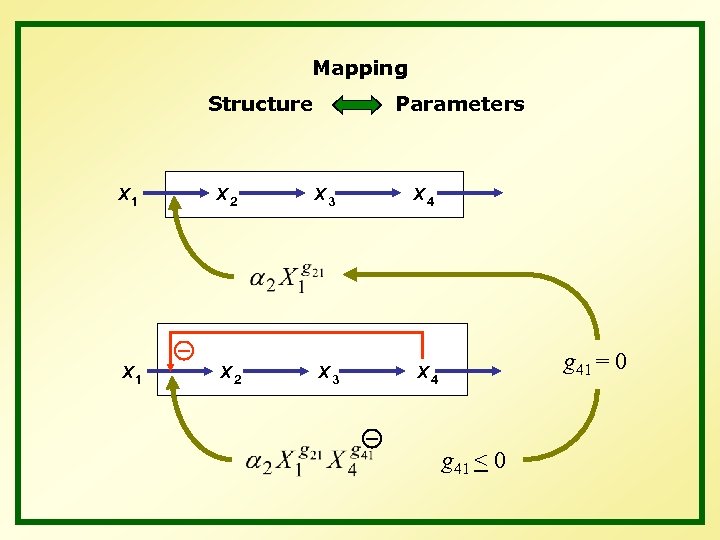
Mapping Structure Parameters X 1 X 2 X 3 X 4 g 41 = 0 g 41 < 0
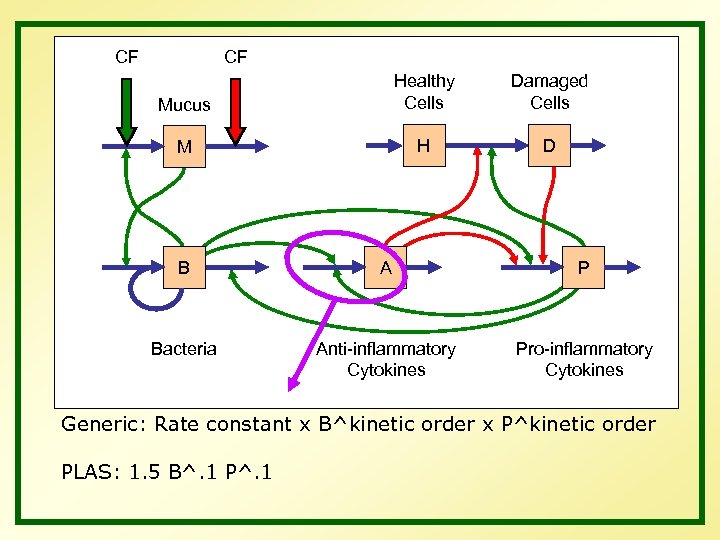
CF CF Mucus Healthy Cells Damaged Cells M H D B A P Bacteria Anti-inflammatory Cytokines Pro-inflammatory Cytokines Generic: Rate constant x B^kinetic order x P^kinetic order PLAS: 1. 5 B^. 1 P^. 1
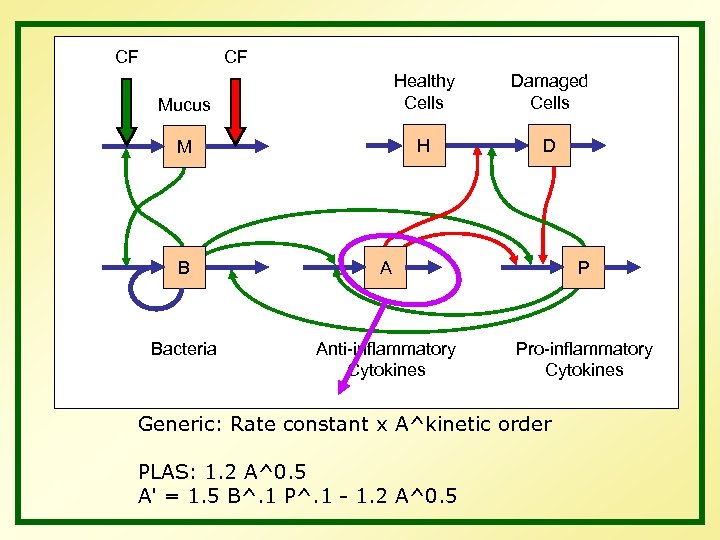
CF CF Mucus Healthy Cells Damaged Cells M H D B A P Bacteria Anti-inflammatory Cytokines Pro-inflammatory Cytokines Generic: Rate constant x A^kinetic order PLAS: 1. 2 A^0. 5 A' = 1. 5 B^. 1 P^. 1 - 1. 2 A^0. 5
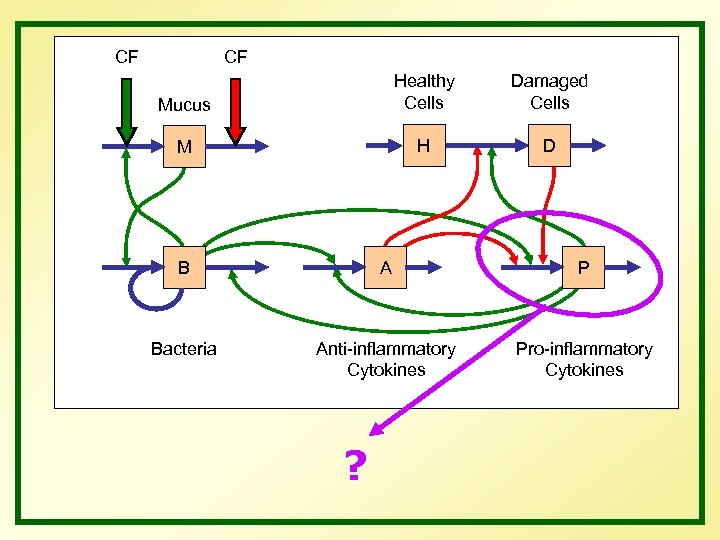
CF CF Mucus Healthy Cells Damaged Cells M H D B A P Bacteria Anti-inflammatory Cytokines Pro-inflammatory Cytokines ?
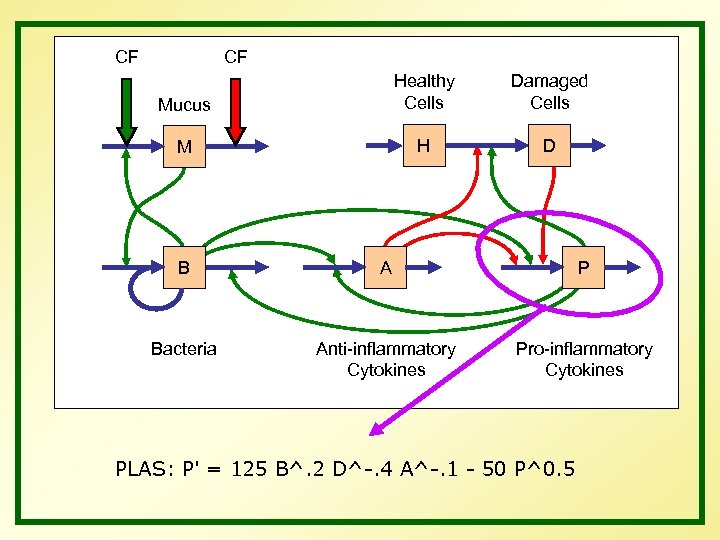
CF CF Mucus Healthy Cells Damaged Cells M H D B A P Bacteria Anti-inflammatory Cytokines Pro-inflammatory Cytokines PLAS: P' = 125 B^. 2 D^-. 4 A^-. 1 - 50 P^0. 5
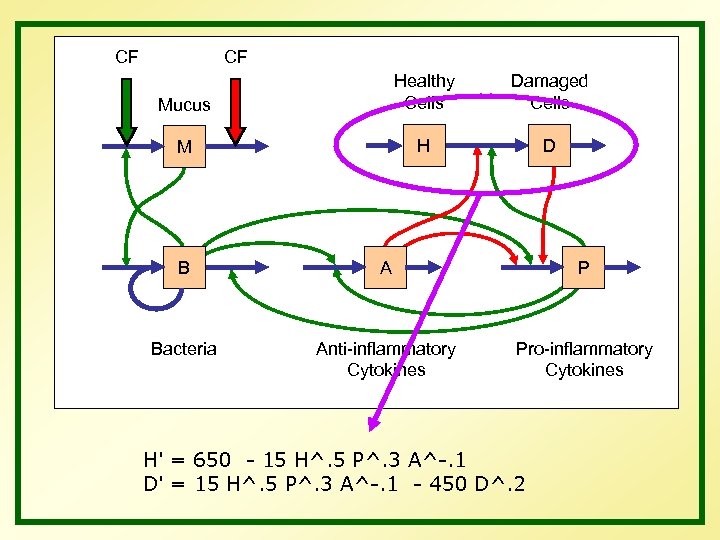
CF CF Mucus Healthy Cells Damaged Cells M H D B A P Bacteria Anti-inflammatory Cytokines Pro-inflammatory Cytokines H' = 650 - 15 H^. 5 P^. 3 A^-. 1 D' = 15 H^. 5 P^. 3 A^-. 1 - 450 D^. 2
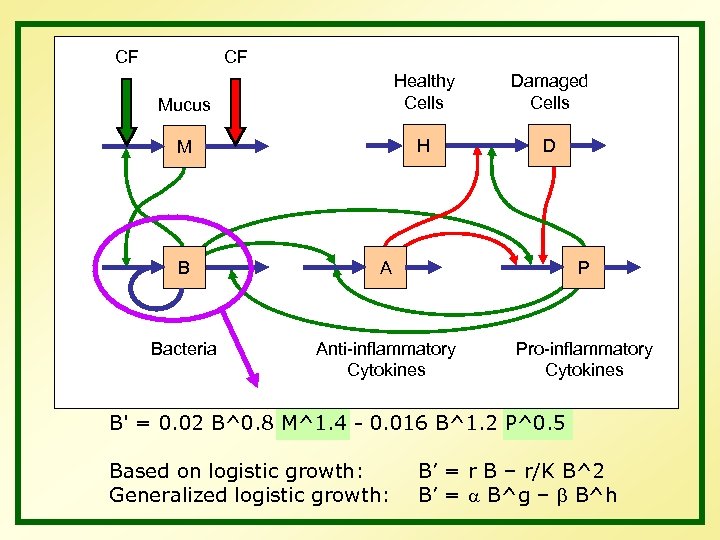
CF CF Mucus Healthy Cells Damaged Cells M H D B A P Bacteria Anti-inflammatory Cytokines Pro-inflammatory Cytokines B' = 0. 02 B^0. 8 M^1. 4 - 0. 016 B^1. 2 P^0. 5 Based on logistic growth: Generalized logistic growth: B’ = r B – r/K B^2 B’ = a B^g – b B^h
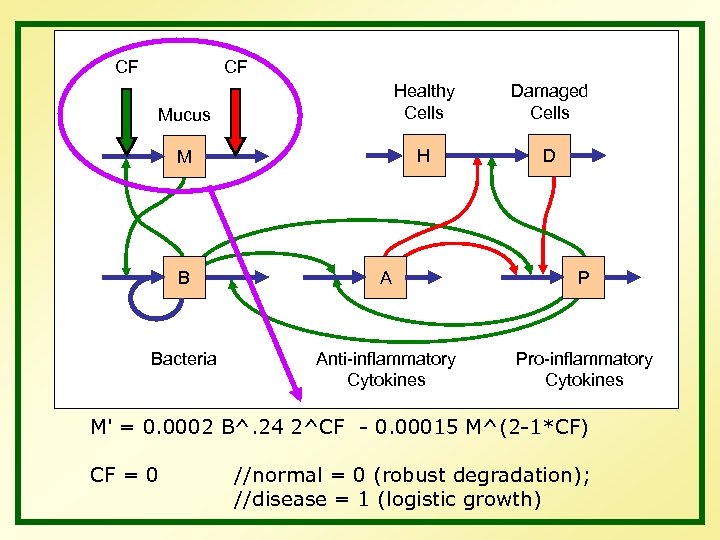
CF CF Mucus Healthy Cells Damaged Cells M H D B A P Bacteria Anti-inflammatory Cytokines Pro-inflammatory Cytokines M' = 0. 0002 B^. 24 2^CF - 0. 00015 M^(2 -1*CF) CF = 0 //normal = 0 (robust degradation); //disease = 1 (logistic growth)

PLAS file: B' = 0. 02 B^0. 8 M^1. 4 - 0. 016 B^1. 2 P^. 5 P' = 125 B^. 2 D^-. 4 A^-. 1 - 50 P^0. 5 A' = 1. 5 B^. 1 P^. 1 - 1. 2 A^0. 5 H' = 650 - VHD D' = VHD - 450 D^. 2 M' = 0. 0002 B^. 24 2^CF - 0. 00015 M^(2 -1*CF) VHD = 15 H^. 5 P^. 3 A^-. 1 CF = 0 B = 2. 064052 // set at steady state, but not very important P = 1. 669952 A = 2. 001266 H = 1585. 926 D = 6. 28788 M = 1. 259609 t 0 = 0 tf = 2000 hr= 1 http: //enzymology. fc. ul. pt/software. htm
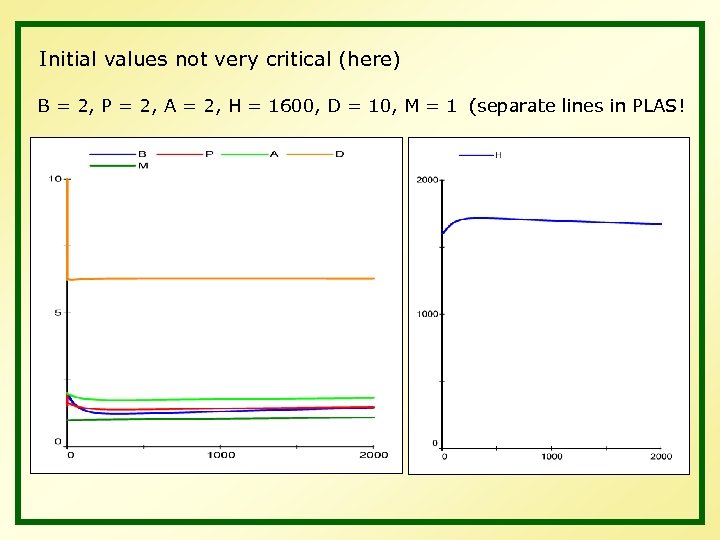
Initial values not very critical (here) B = 2, P = 2, A = 2, H = 1600, D = 10, M = 1 (separate lines in PLAS!
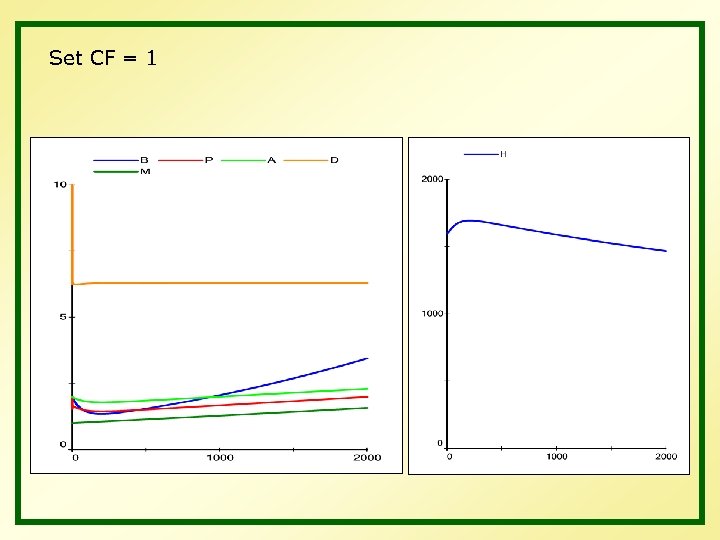
Set CF = 1
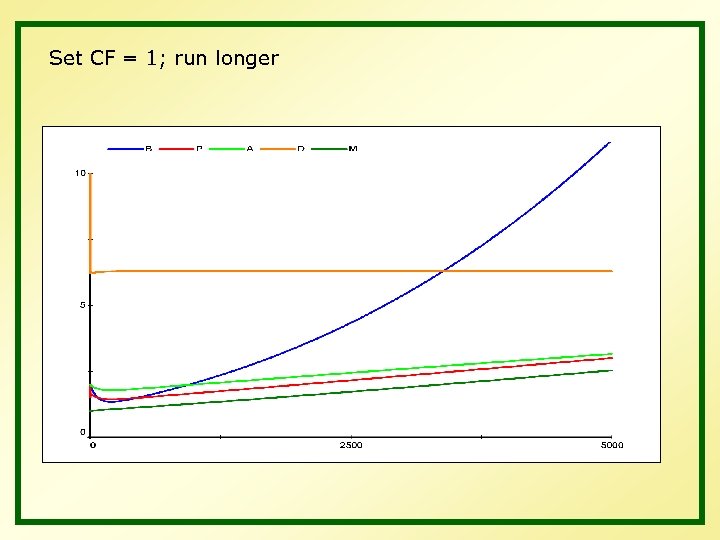
Set CF = 1; run longer
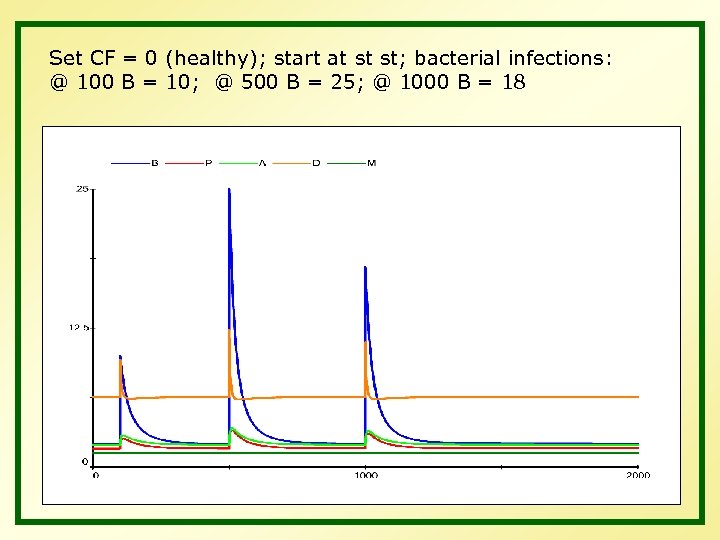
Set CF = 0 (healthy); start at st st; bacterial infections: @ 100 B = 10; @ 500 B = 25; @ 1000 B = 18
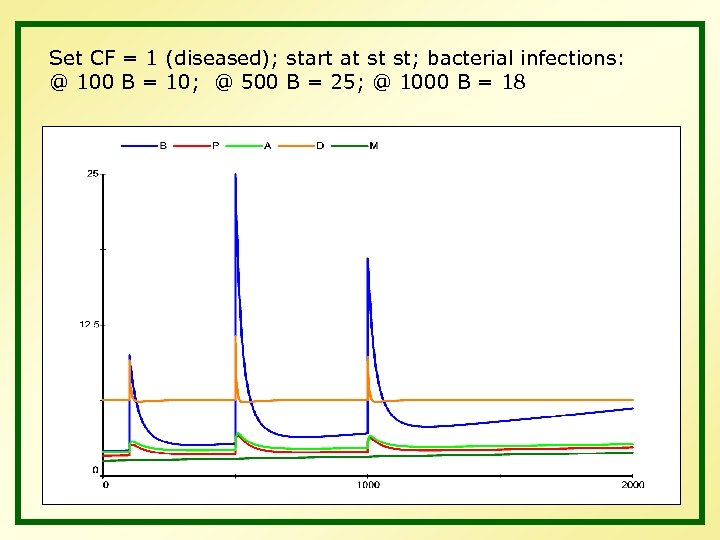
Set CF = 1 (diseased); start at st st; bacterial infections: @ 100 B = 10; @ 500 B = 25; @ 1000 B = 18
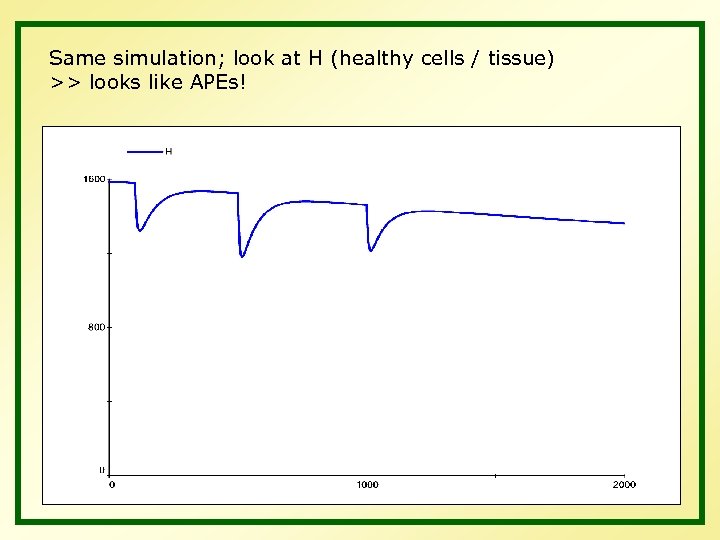
Same simulation; look at H (healthy cells / tissue) >> looks like APEs!
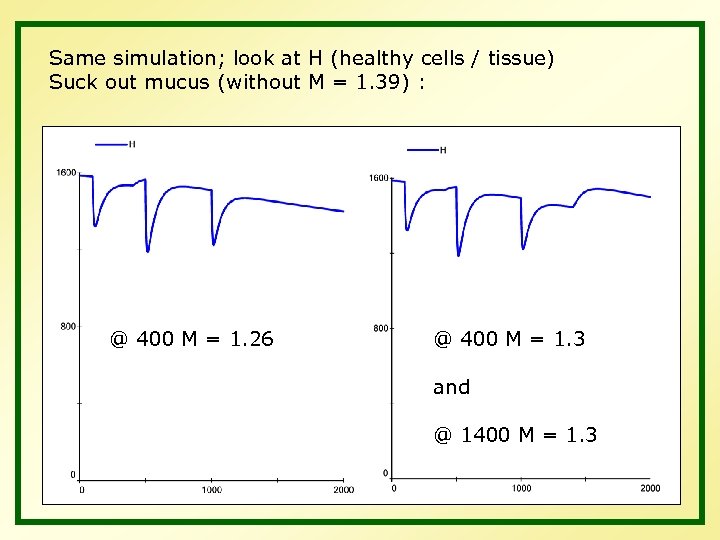
Same simulation; look at H (healthy cells / tissue) Suck out mucus (without M = 1. 39) : @ 400 M = 1. 26 @ 400 M = 1. 3 and @ 1400 M = 1. 3
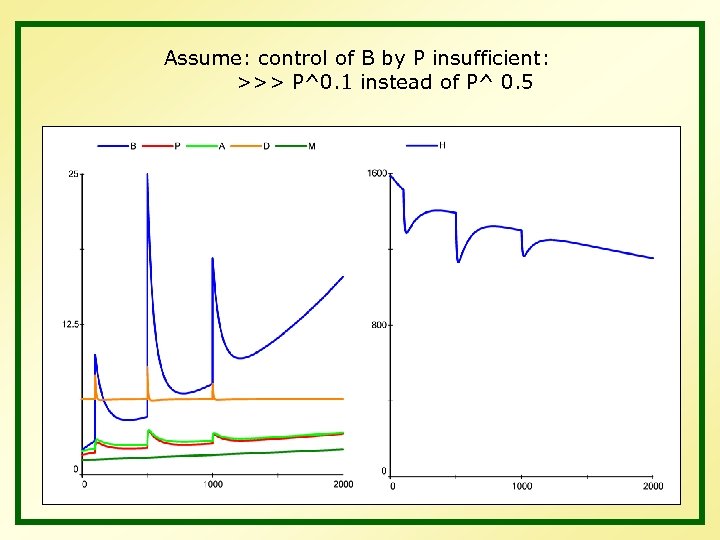
Assume: control of B by P insufficient: >>> P^0. 1 instead of P^ 0. 5
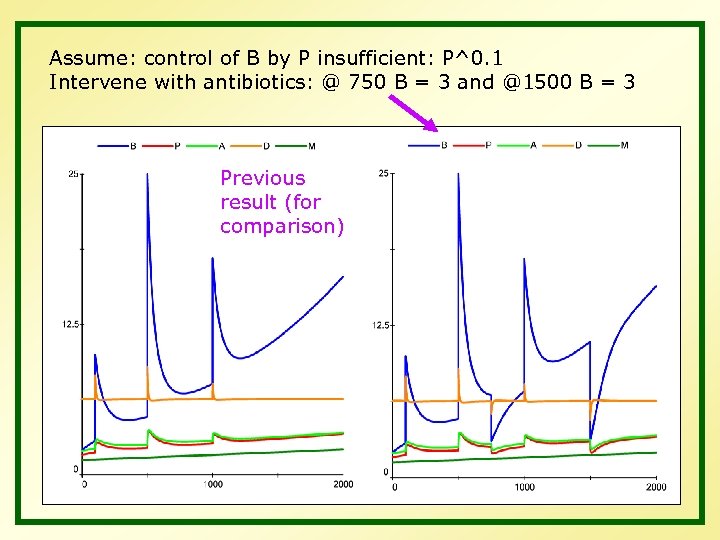
Assume: control of B by P insufficient: P^0. 1 Intervene with antibiotics: @ 750 B = 3 and @1500 B = 3 Previous result (for comparison)

Many scenarios possible: Frequency of infections Anti-inflammatory drugs (one time; permanent) Partial bacterial resistance Bacteria with higher carrying capacity Several bacterial species Effects of parameter values
Life is complicated! Cytokines need to be in balance; cytokine storms can be fatal
Life is complicated! Cytokines interact in complicated ways
Life is complicated! Cytokines affect numerous vital processes
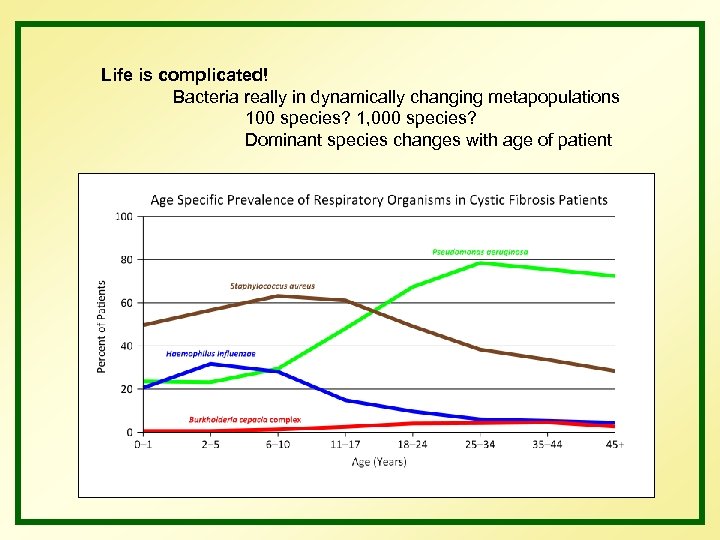
Life is complicated! Bacteria really in dynamically changing metapopulations 100 species? 1, 000 species? Dominant species changes with age of patient
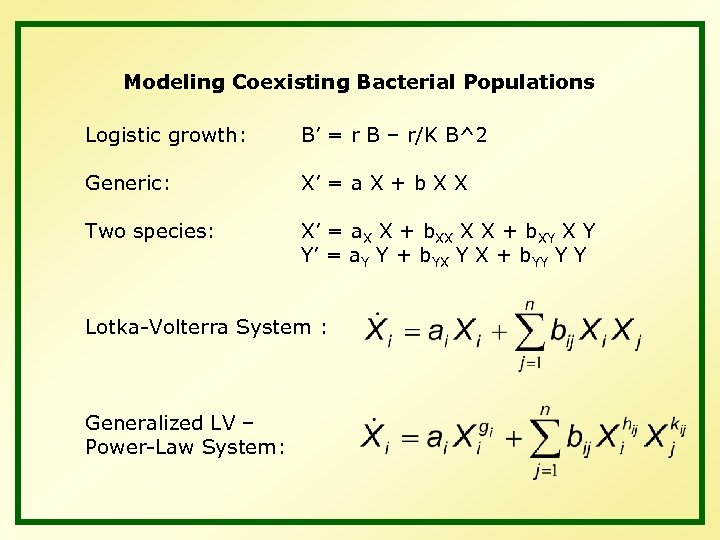
Modeling Coexisting Bacterial Populations Logistic growth: B’ = r B – r/K B^2 Generic: X’ = a X + b X X Two species: X’ = a. X X + b. XX X X + b. XY X Y Y’ = a. Y Y + b. YX Y X + b. YY Y Y Lotka-Volterra System : Generalized LV – Power-Law System:
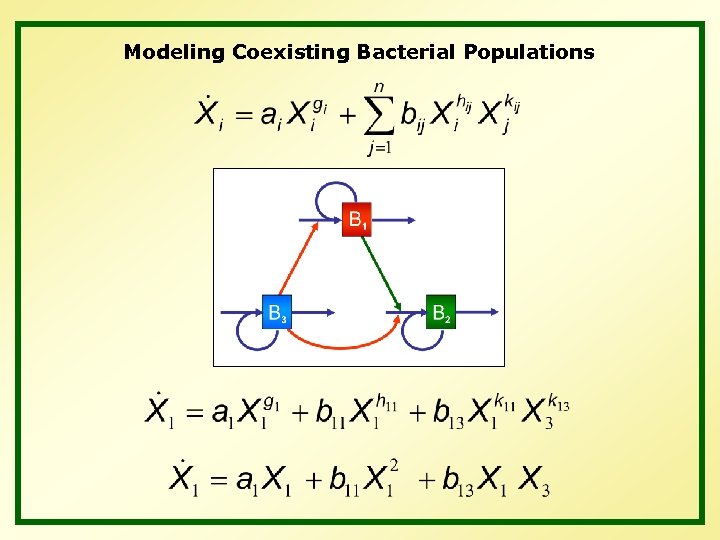
Modeling Coexisting Bacterial Populations
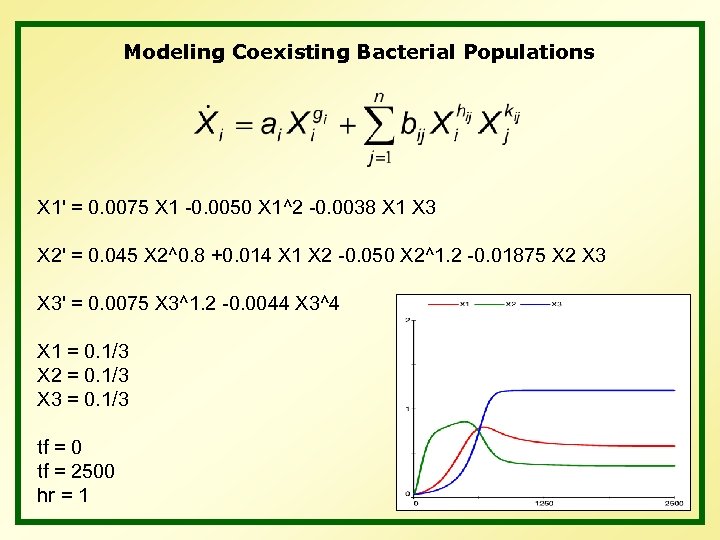
Modeling Coexisting Bacterial Populations X 1' = 0. 0075 X 1 -0. 0050 X 1^2 -0. 0038 X 1 X 3 X 2' = 0. 045 X 2^0. 8 +0. 014 X 1 X 2 -0. 050 X 2^1. 2 -0. 01875 X 2 X 3' = 0. 0075 X 3^1. 2 -0. 0044 X 3^4 X 1 = 0. 1/3 X 2 = 0. 1/3 X 3 = 0. 1/3 tf = 0 tf = 2500 hr = 1
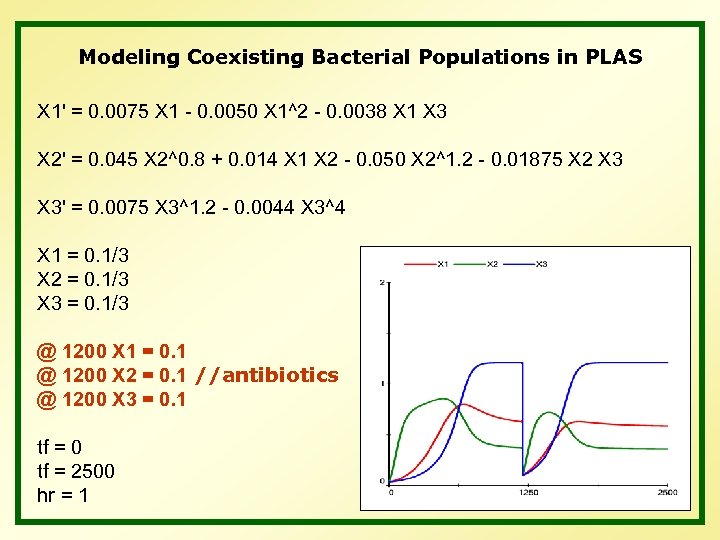
Modeling Coexisting Bacterial Populations in PLAS X 1' = 0. 0075 X 1 - 0. 0050 X 1^2 - 0. 0038 X 1 X 3 X 2' = 0. 045 X 2^0. 8 + 0. 014 X 1 X 2 - 0. 050 X 2^1. 2 - 0. 01875 X 2 X 3' = 0. 0075 X 3^1. 2 - 0. 0044 X 3^4 X 1 = 0. 1/3 X 2 = 0. 1/3 X 3 = 0. 1/3 @ 1200 X 1 = 0. 1 @ 1200 X 2 = 0. 1 //antibiotics @ 1200 X 3 = 0. 1 tf = 0 tf = 2500 hr = 1
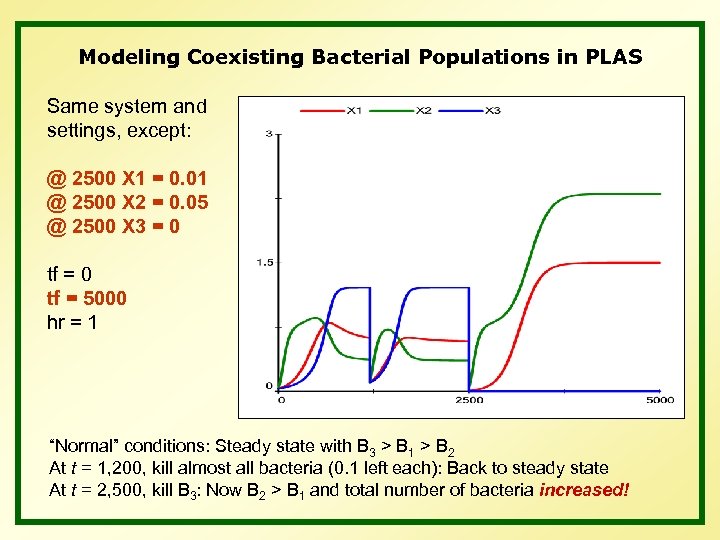
Modeling Coexisting Bacterial Populations in PLAS Same system and settings, except: @ 2500 X 1 = 0. 01 @ 2500 X 2 = 0. 05 @ 2500 X 3 = 0 tf = 5000 hr = 1 “Normal” conditions: Steady state with B 3 > B 1 > B 2 At t = 1, 200, kill almost all bacteria (0. 1 left each): Back to steady state At t = 2, 500, kill B 3: Now B 2 > B 1 and total number of bacteria increased!

Summary Complex system Very simple model; generic parameter values Some insights Tool for fast testing and exploration Uncounted scenarios possible Starting point for more and better things
5f730345d895cd00b4eac0972eb64085.ppt