SETS A set is a collection of elements

SETS A set is a collection of elements We write Costas Busch - RPI 1

Set Representations C = { a, b, c, d, e, f, g, h, i, j, k } C = { a, b, …, k } finite set S = { 2, 4, 6, … } infinite set S = { j : j > 0, and j = 2 k for some k>0 } S = { j : j is nonnegative and even } Costas Busch - RPI 2

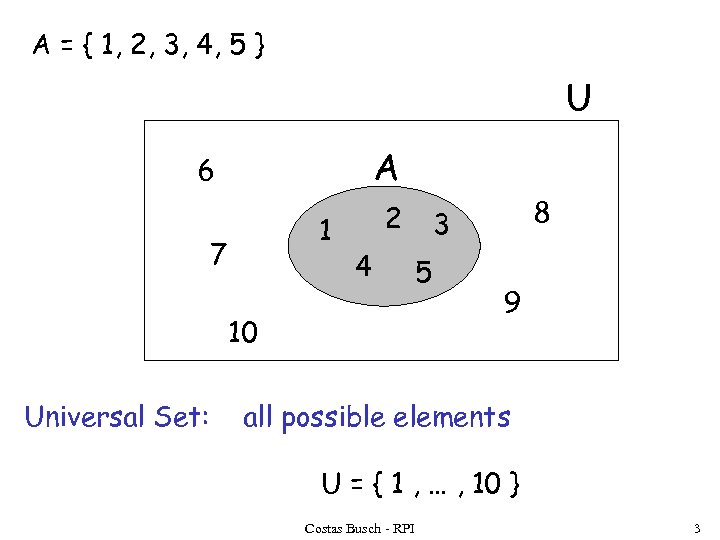A = { 1, 2, 3, 4, 5 } U A 6 1 7 2 4 10 Universal Set: 8 3 5 9 all possible elements U = { 1 , … , 10 } Costas Busch - RPI 3

Set Operations A = { 1, 2, 3 } B = { 2, 3, 4, 5} B A • Union A U B = { 1, 2, 3, 4, 5 } 2 3 1 4 5 • Intersection U A B = { 2, 3 } 2 3 • Difference A-B={1} 1 B - A = { 4, 5 } Venn diagrams Costas Busch - RPI 4

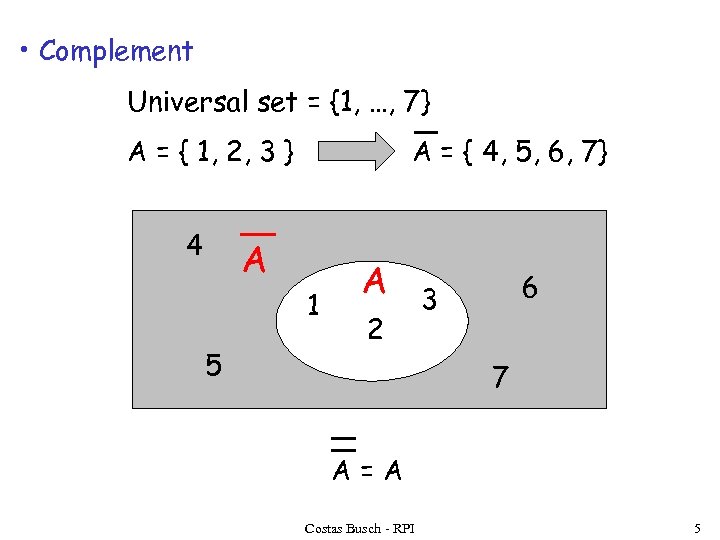• Complement Universal set = {1, …, 7} A = { 1, 2, 3 } 4 A = { 4, 5, 6, 7} A 1 5 A 2 6 3 7 A=A Costas Busch - RPI 5

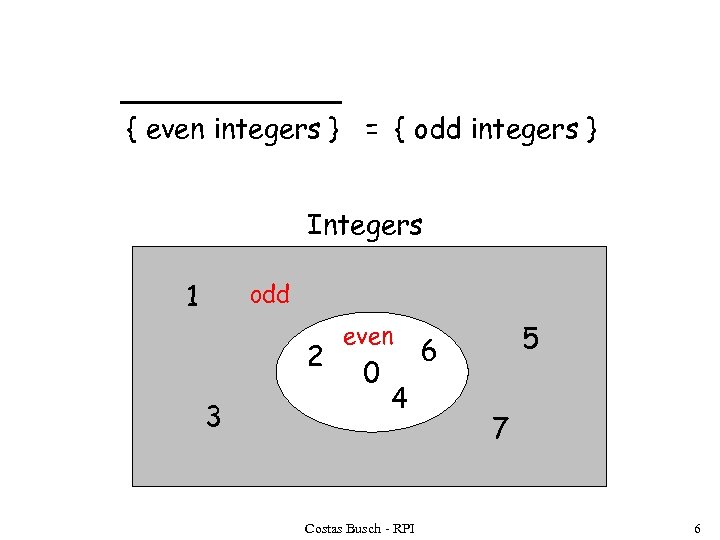{ even integers } = { odd integers } Integers 1 odd 2 3 even 0 4 Costas Busch - RPI 5 6 7 6

De. Morgan’s Laws U AUB=A B B=AUB Costas Busch - RPI 7

Empty, Null Set: ={} SU =S S = U S- = Universal Set =S -S= Costas Busch - RPI 8

Subset A = { 1, 2, 3} B = { 1, 2, 3, 4, 5 } U Proper Subset: A B U A B B A Costas Busch - RPI 9

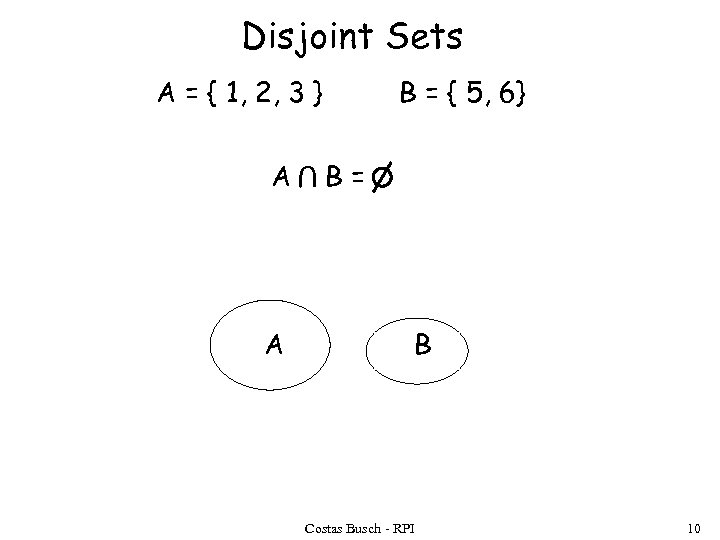Disjoint Sets A = { 1, 2, 3 } A U A B = { 5, 6} B= B Costas Busch - RPI 10

Set Cardinality • For finite sets A = { 2, 5, 7 } |A| = 3 (set size) Costas Busch - RPI 11

Powersets A powerset is a set of sets S = { a, b, c } Powerset of S = the set of all the subsets of S 2 S = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } Observation: | 2 S | = 2|S| Costas Busch - RPI ( 8 = 23 ) 12

Cartesian Product A = { 2, 4 } B = { 2, 3, 5 } A X B = { (2, 2), (2, 3), (2, 5), ( 4, 2), (4, 3), (4, 5) } |A X B| = |A| |B| Generalizes to more than two sets AXBX…XZ Costas Busch - RPI 13

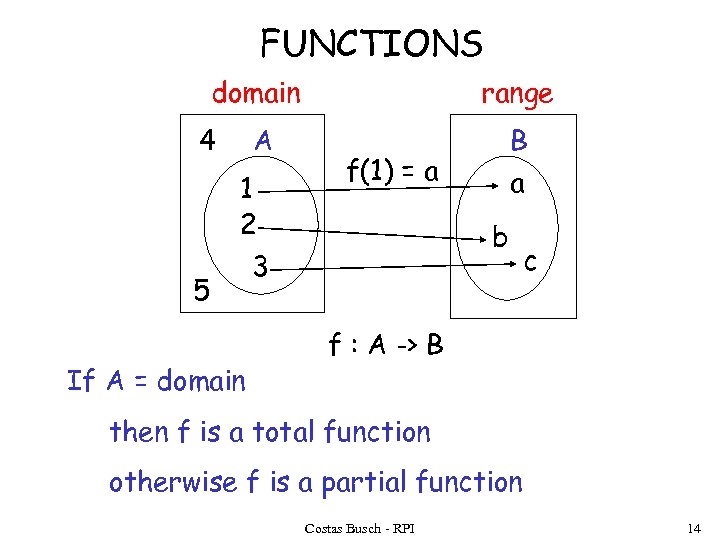FUNCTIONS domain 4 5 A 1 2 3 If A = domain range B f(1) = a a b c f : A -> B then f is a total function otherwise f is a partial function Costas Busch - RPI 14

RELATIONS R = {(x 1, y 1), (x 2, y 2), (x 3, y 3), …} x i R yi e. g. if R = ‘>’: 2 > 1, 3 > 2, 3 > 1 Costas Busch - RPI 15

Equivalence Relations • Reflexive: x. Rx • Symmetric: x. Ry • Transitive: x R y and y R z y. Rx x. Rz Example: R = ‘=‘ • x=x • x=y • x = y and y = z y=x x=z Costas Busch - RPI 16

Equivalence Classes For equivalence relation R equivalence class of x = {y : x R y} Example: R = { (1, 1), (2, 2), (1, 2), (2, 1), (3, 3), (4, 4), (3, 4), (4, 3) } Equivalence class of 1 = {1, 2} Equivalence class of 3 = {3, 4} Costas Busch - RPI 17

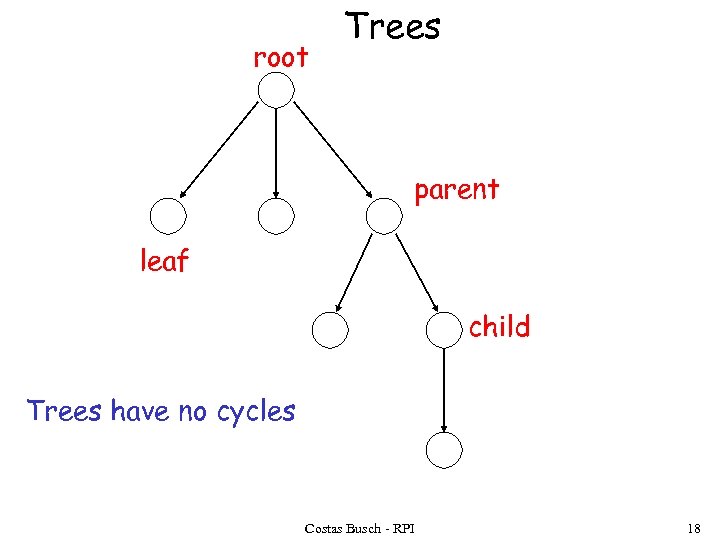root Trees parent leaf child Trees have no cycles Costas Busch - RPI 18

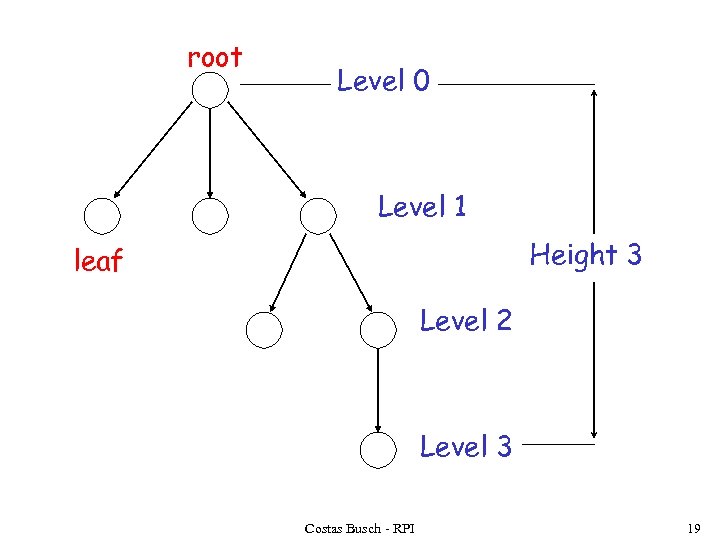root Level 0 Level 1 Height 3 leaf Level 2 Level 3 Costas Busch - RPI 19

Binary Trees Costas Busch - RPI 20

Languages Costas Busch - RPI 21

A language is a set of strings String: A sequence of letters Examples: “cat”, “dog”, “house”, … Defined over an alphabet: Costas Busch - RPI 22

Alphabets and Strings We will use small alphabets: Strings Costas Busch - RPI 23

String Operations Concatenation Costas Busch - RPI 24

Reverse Costas Busch - RPI 25

String Length: Examples: Costas Busch - RPI 26

Length of Concatenation Example: Costas Busch - RPI 27

Empty String A string with no letters: Observations: Costas Busch - RPI 28

Substring of string: a subsequence of consecutive characters String Substring Costas Busch - RPI 29

Prefix and Suffix Prefixes Suffixes prefix suffix Costas Busch - RPI 30

Another Operation Example: Definition: Costas Busch - RPI 31

The * Operation : the set of all possible strings from alphabet Costas Busch - RPI 32

The + Operation : the set of all possible strings from alphabet except Costas Busch - RPI 33

Languages A language is any subset of Example: Languages: Costas Busch - RPI 34

Note that: Sets Set size String length Costas Busch - RPI 35

Another Example An infinite language Costas Busch - RPI 36

Operations on Languages The usual set operations Complement: Costas Busch - RPI 37

Reverse Definition: Examples: Costas Busch - RPI 38

Concatenation Definition: Example: Costas Busch - RPI 39

Another Operation Definition: Special case: Costas Busch - RPI 40

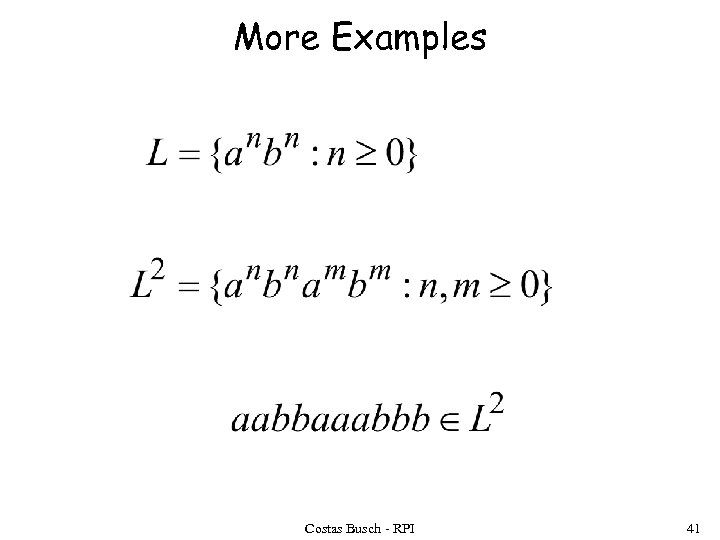More Examples Costas Busch - RPI 41

Star-Closure (Kleene *) Definition: Example: Costas Busch - RPI 42

Positive Closure Definition: Costas Busch - RPI 43