Сети Петри Глава 11 Стохастические сети Петри Aurelia

Сети Петри Глава 11. Стохастические сети Петри Aurelia Prepelita Conf. , dr. , USM Chisinau, 2010

Оглавление: Глава 11. Стохастические сети Петри § Стохастические процессы. Основные понятия § Вводные понятия и основные определения § § Стационарные процессы Независимые процессы Марковские процессы Цепи Маркова § Стохастические временные СП § Марковские сети Петри

Стохастические процессы. Основные понятия По определению, стохастический процесс представляет собой семейство случайных величин X( ) принадлежащих пространству Wx( ), называемое пространством состояний и которые индексируются по параметру значения которых принадлежат ансамблю . Это означает, что процесс представляется как: {X( ) Wx( ), }. Ансамбли Wx и могут быть дискретным или непрерывным. В зависимости от того принимает ли данный параметр непрерывные или дискретные значения, то будем говорить либо о стохастической цепи, либо о стохастическом процессе. Часто параметр представляет время.

Стохастические процессы. Основные понятия Для оценки состояния системы необходимо использовать вектор состояния X, представленный семейством X( i) случайных величин, независимых между собой: X={X( 1), X( 2), …, X( i), …}. Необходимо ввести понятие вероятности состояния x( ): x( )=Prob{X( )=x}, является функцией параметра и представляющая вероятность того, что переменная X примет значение х в момент ; Это значение фактически представляет собой абсолютную вероятность состояния X( ).

Стохастические процессы. Основные понятия Условная вероятность перехода от состояния x 1 к x 2 , через один или несколько временнных прыжков: rx 1 x 2( 1, 2)=Prob{X( 2)=x 2|X( 1)=x 1} и представляет вероятности перехода между двумя этими двумея состояниями, события, которые разворачиваются в промежутке времени = 2 - 1. Стохастические процессы в соответствии с фунцией распределения вероятностей - Fx(X, ): Fx(X, )=Prob{X( 1)≤x 1, X( 2)≤x 2, …, X( i)≤xi, …} делятся на: стационарные процессы, независимые процессы, Марковские процессы.

Стационарные, независимые, Марковские процессы Стационарные процессы Процесс X( ) является стационарным, если функция распределения вероятностей остается равной себе на любом промежутке на оси времени, а именно: Fx(X, + )= Fx(X, ); Независимые процессы Концепция независимости между переменными X( i) представлена в ввиде: Fx(X, )=Fx 1, x 2, …, xi, …(x 1, x 2, …, xi, …, 1, 2, …, I, …)=Fx 1(x 1, 1)*Fx 2(x 2, 2)*…*Fxi(xi, i)*…; Марковские процессы Эта категория охватывает случайные процессы для которых изменения происходят, таким образом что каждое из состояний X( 0), X( 1), …, X( i), … соответствующие последовательным моментам 0, 1, …, i, … зависят только от конечного числа k предыдущих состояний. Если пространство состояний дискретно, то мы имеем дело с цепью Маркова порядка k. Наиболее часто используется класс Марковских процессов, для которых k= 1. Это означает, что если дана последовательность состояний X( j) для такого процесса, состояние X( j+1) будет зависеть исключительно от предыдущего X( j) состояния т. е. с точки зрения вероятности: Prob{Xj+1( j+1=xj+1|X( 0=x 0, …, X( j=xj}= Prob{X( j+1=xj+1|X( j=xj}.

Марковские процессы Это свойство представляет собой основную характеристику Марковского процесса: будущее состояние зависит только от настоящего состояния. Иными словами, Марковские процессы -процессы без памяти.

Цепи Маркова Если n(j) является абсолютной вероятностью состояния nj, то пространство вероятности на момент j представляет собой матрицу-строку П (j), компонентами которой являются значения 0(j), 1(j), …, каждое из которых имея амплитуду (j) меньшую или равную единице, т. е. : П(j) =[ 0(j), 1(j), …, k(j), …]. (j) ), … зная, что для любого nj ≥ 0 существует: 0≤ ni ≤ 1 cu ni ni (j)=1.

Вводные понятия и основные определения

Вводные понятия и основные определения Стохастические процессы позволяют моделировать множество технических, экономических, социальных и др. систем.

Вводные понятия и основные определения Далее, введем расширение Марковских сетей Петри которые используем для моделирования и оценки эффективности вычислительных систем.

Марковские сети Петри Если все функции распределения случайных величин, экспоненциально-отрицательны, то процесс маркировки данной сети описывается однородным непрерывным во времени Марковским процессом. Для каждого момента времени у отрицательно экспоненциального закона память (о предыдущих состояниях) отсутствует. В этом случае мы имеем следующие функции распределения для случайной продолжительности : где скорость срабатывания перехода.

Марковские сети Петри Определение. Обобщенная сеть Петри-Маркова, RPM сокращенно, есть 2 -ка NM=, где: - N обобщенная СП; - является функцией, определяющая скорость срабатывания возбужденных переходов маркировкой M, т. е. параметр отрицательно экспоненциального закона: .

Марковские сети Петри В общем, если система описывается Марковским процессом с непрерывным временем, определяющий цепь Маркова с непрерывным временем (МЦНВ), тогда он определяет существование стационарного режима и позволяет проводить численные оценки средних значений характеристик исследуемой системы. Стационарное состояние функционирования системы представляет собой такой режим, при котором эволюция системы не зависит ни от начальных условий, ни от данного момента времени. Если все состояния МЦНВ могут быть достигнуты в течение ограниченного промежутка времени, то существует стационарное распределение вероятностей нахождения в соответствующих состояниях.

Марковские сети Петри Система, моделируемая RPM, будет обладать стабильными режимами функционирования, если соответствующая ей обобщенная СП ограничена, жизнеспособна и, реинициализуема. Эти три свойства обобщенной СП гарантируют что граф достижимых маркировок будет изоморфен МЦНВ для ОСП.

Динамическая матрица МЦНВ. Цепь МЦНВ, описывающая функционирование RPM может быть получена непосредственно из графа достижимых маркировок ОСП, представленный в виде списка. Пространство состояний МЦНВ является Acc(RP, M 0), и скорости перехода от заданной маркировки Mi к новой маркировке Mj, (Mi[tk>Mj) определяются по формуле dij= k>0, i j, где k скорость срабатывания перехода tk (возможно от маркировки зависимая, т. е. , например, k(Mi)= k* Mi(pi)). Если существуют два или более возбужденных переходов tk 1, tk 2, . . . которые в свою очередь приводят от маркировки Mi к маркировке Mj, (i j), то dij= k 1 +. . . , и.

Динамическая матрица МЦНВ Квадратная матрица порядка Ns = Acc (RP, М 0) называется динамической матрицей, описывающей ЦМНВ и соответствующая ОСП. Функционирование ЦМНВ описывается системой уравнений Колмогорова-Чепмена: где i( ) есть вероятность, что маркировка ОСП в данный момент времени будет Mi, и 0(0)=1. Приведем другой вид уравнения Чепмена-Колмогорова: П * D = 0; где i – стационарная вероятность что ОСП будет находиться в маркировке Mi, а П=( 0, 1, . . . , Ns) есть вектор-строка.

Численные характеристики производительности систем Определив вероятности стационарного состояния П, можно оценить различные характеристики производительности компьютерных систем описанных моделями ОСП Маркова. Далее мы рассмотрим некоторые численные характеристики производительности систем: 1. Предположим B Acc(RP, M 0) является подмножеством состояний цепи ЦМНВ определяющее частное условие вероятности появления некоторых событий, таких что Марковский процесс принадлежал бы подмножеству состояний B, то мы получим следующее соотношение:

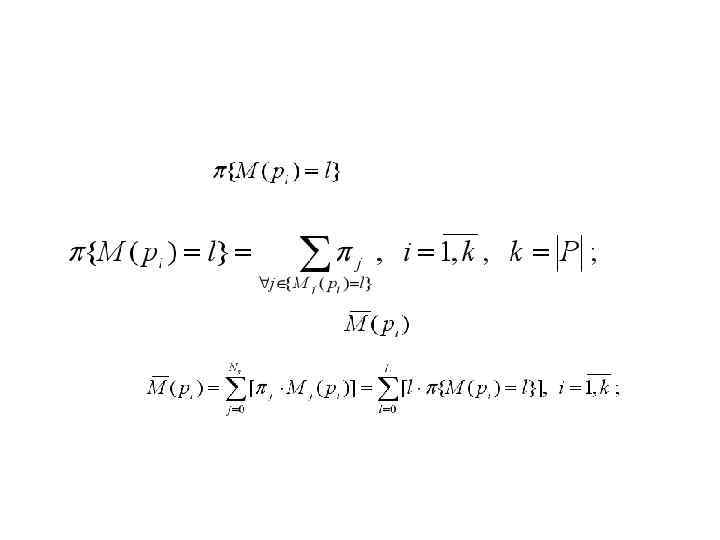Численные характеристики производительности систем 2. Вероятность что в позиции pi, L – ограниченной, находятся ровно l=(0, . . . , L) маркеров: 3. Среднее число маркеров в позиции pi:

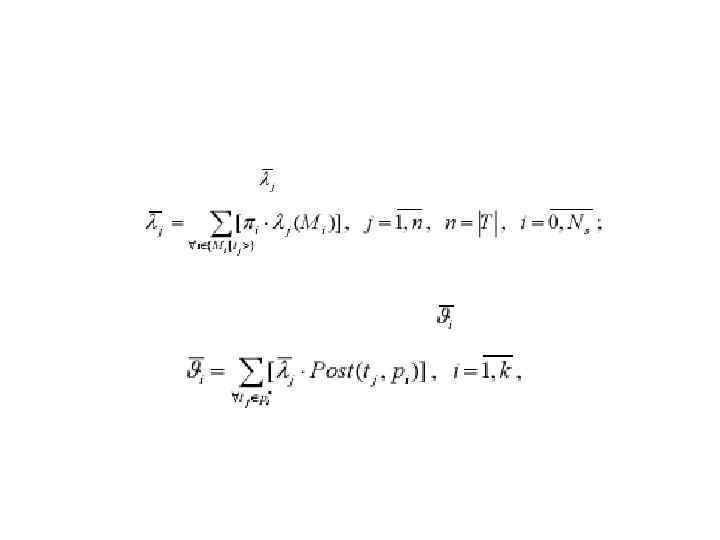Численные характеристики производительности систем 4. Средняя скорость срабатывания перехода tj: 5. Средняя скорость входного потока в позицию pi:

Численные характеристики производительности систем 6. Средняя скорость из позиции pi: выходного потока 7. Вероятность что число маркеров в позиции ограниченно

Численные характеристики производительности систем 8. Средняя частота перехода tj: 9. Среднее время позиции pi: срабатывания нахождения маркера в

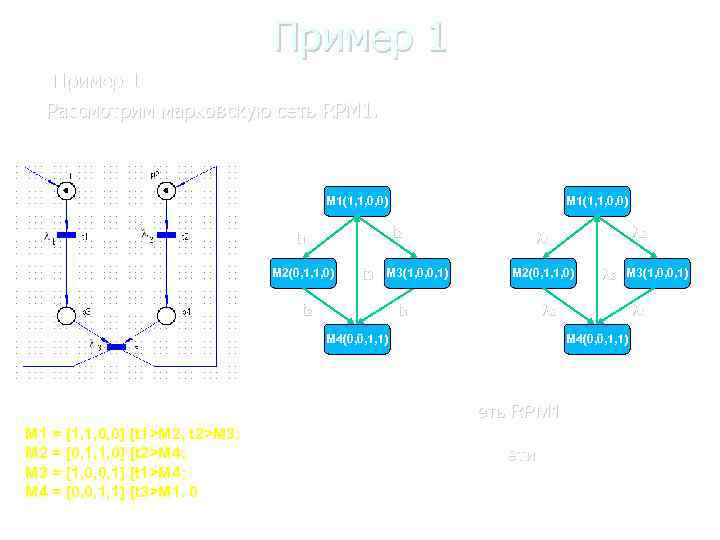Пример 1 Рассмотрим марковскую сеть RPM 1. M 1(1, 1, 0, 0) t 2 t 1 M 2(0, 1, 1, 0) t 3 M 3(1, 0, 0, 1) t 1 t 2 M 4(0, 0, 1, 1) c) a) M 1 = [1, 1, 0, 0] [t 1>M 2, t 2>M 3; M 2 = [0, 1, 1, 0] [t 2>M 4; M 3 = [1, 0, 0, 1] [t 1>M 4; M 4 = [0, 0, 1, 1] [t 3>M 1. 0 b) M 1(1, 1, 0, 0) 2 1 3 M 2(0, 1, 1, 0) M 3(1, 0, 0, 1) 2 1 M 4(0, 0, 1, 1) d) Рисунок 1. Марковская сеть RPM 1 (a); Граф достижимости в виде списка (b); Граф достижимости марковской сети RPM 1 (c) Цепь Маркова LM 1 (d).

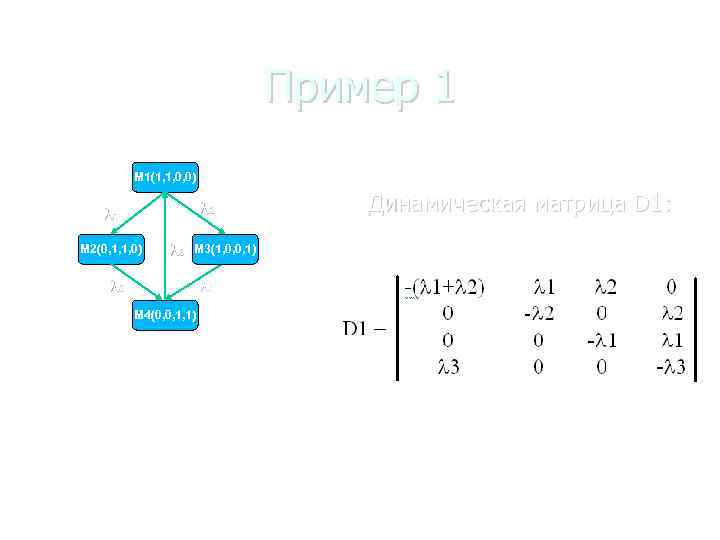Пример 1 M 1(1, 1, 0, 0) 1 2 1 M 2(0, 1, 1, 0) 1 3 M 3(1, 0, 0, 1) 1 2 1 M 4(0, 0, 1, 1) Рис. 3. Цепь Маркова LM 1. Динамическая матрица D 1:

Пример 1 Вектор-строка стационарных вероятностей ∏=[ 1, 2, 3, 4] нахождения в состояниях Mi(i=1, 4) является решением системы уравнений Колмогорова: {

Пример 1 Находим: Средние скорости срабатывания переходов RPS 1:

Пример 1 Т. о. , вектор-строка =[ 1, 2, 3] является решением уравнения C* =0, где C матрица инциденций сети RPM 1. Средние значения маркировок M (pi) в соответствующих позициях определяются как:

Пример 1 Которые определяют уловия консервирования маркировок в позициях: С помощью формулы Little можно определить среднее время (pi) нахождения маркеров в соответствующих позициях:

Численные характеристики производительности систем. Пример 2. Проиллюстрируем применение ССП Маркова для моделирования вычислительных систем. Рассмотрим упрощенную модель многопроцессорной системы с n активными процессорами, которые могут выйти из строя, и с К процессорами в хорошем рабочем состоянии, что находится в резерве. При отказе какого-либо процессора в активном состоянии, то он будет заменен на один процессор из числа резервных. Процессор вышедший из строя будет отремонтирован, а затем будет направлен в резерв. Состояния: Р 1 число активных процессоров в хорошем, рабочем состоянии; Р 2 число процессоров в хорошем рабочем состоянии, что находится в резерве и которые могут быть использованы для замены вышедших из строя процессоров, находящихся в активном состоянии; P 3 это число процессоров в аварии и P 4 определяет количество процессоров в настоящее время нуждаются в ремонте. Основными событиями являются: 1 сбой процессора находящегося в активном состоянии; 2 замена процессора на резервный процессор; 3 ремонт процесса, который затем направляется в резерв.

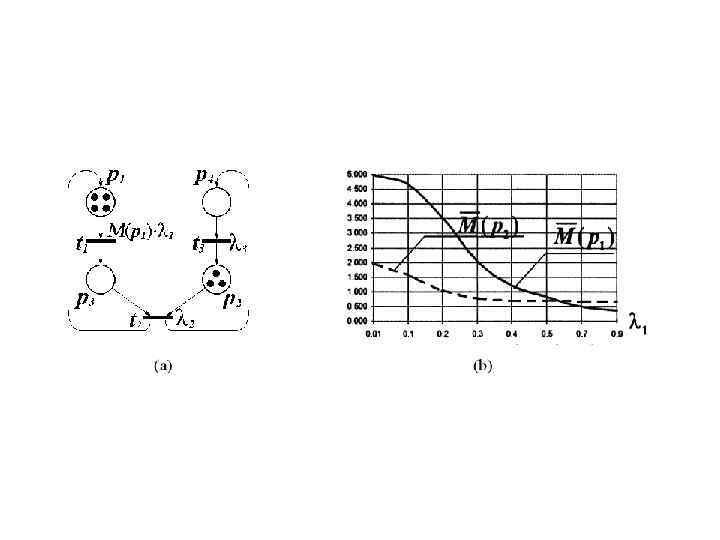Численные характеристики производительности систем. Пример 2. Рисунок 1. ССПМ(а) и производительность работы системы в зависимости от средней скорости сбоя процессора 1 (b).

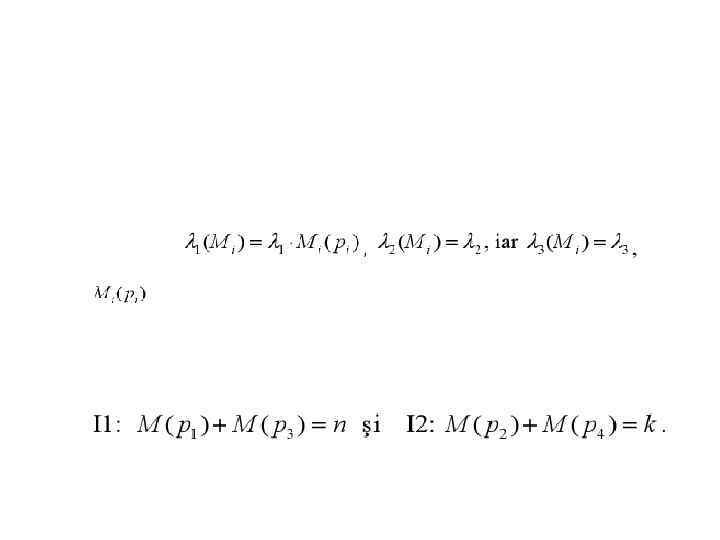Численные характеристики производительности систем. Пример 2. Скорости срабатывания переходов: где число маркеров в позиции pi и маркировке Mi. Можно заметить что ОСП с начальной маркировкой M 0=(n, k, 0, 0) имеет 2 P-инварианта:

Численные характеристики производительности систем. Пример 2. Рассмотренная сеть является ограниченной, живой и реинициализуемой и цепь Маркова обладает Ns=(n+1)(k+1) числом состояний. Для начальной маркировке M 0=(4, 3, 0, 0) цепь Маркова представлена ниже:

Численные характеристики производительности систем. Пример 2. Для начальной маркировке M 0=(5, 2, 0, 0) и значений получим численные значения для характеристик представленных на рис. 2 b.

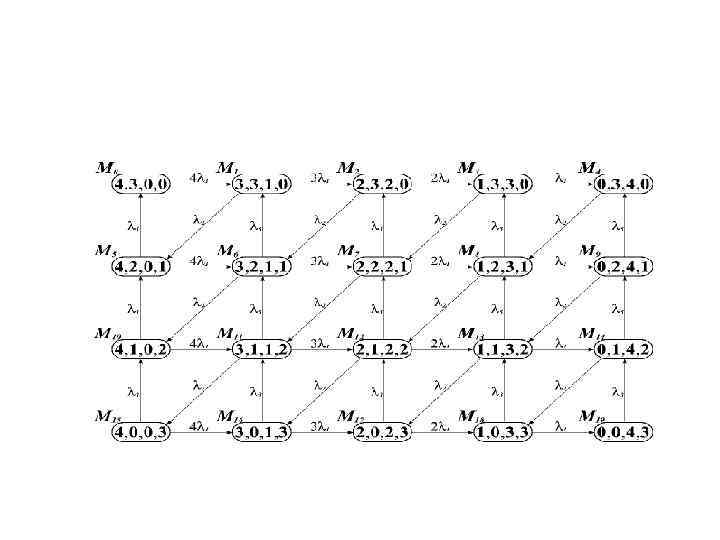Численные характеристики производительности систем. Пример 2. Рисунок. 2. Цепь Маркова с непрерывным временем с начальной маркировкой M 0=(4, 3, 0, 0).

Литература 1. GUTULEAC E. , MOCANU M. L. , TURCANU I. Membrane Differential Petri Nets for Performance Modelling of Hybrid P-Systems. Control Engineering and Applied Informatics, vol. 9, no. 3 -4, December 2007, Ed. : SRAIT, Bucuresti, Romania, p. 12 -21. 2. Guţuleac E. Modelarea şi evaluarea performanţelor sistemelor de calcul prin Reţele Petri: Ciclu de prelegeri. Partea I. Departamentul Editorial-Poligrafic al U. T. M. Chişinău, 1998.