Сетевые модели Сетевые модели Транспортная задача Задача

Сетевые модели

Сетевые модели Транспортная задача Задача о минимальном покрытии Задача о кратчайшем маршруте Задача о максимальном потоке Задача о формировании сети минимальной стоимости • Сетевое планирование • Теория расписаний • • •

Транспортная задача Имеется n складов А 1, А 2, …, Аn, и m потребителей В 1, В 2, …, В m. Объемы запасов товара на складах составляют а 1, а 2, …, аn единиц товара, а объемы потребностей потребителей b 1, b 2, …, bm единиц товара соответственно, Перевозка единицы груза из i-го склада j-му потребителю требует затрат в размере cij (единиц денежных средств), Требуется определить объемы перевозок из складов потребителям, так, чтобы все потребители получили необходимый им объем товара, при этом суммарные затраты на перевозку товаров были минимальными

Формализованная постановка задачи - количество товаров, перевозимое из i-го склад j-му потребителю (1) (2)

Сведение транспортной задачи к ЗЛП

Обобщения транспортной задачи 1. Транспортные задачи с неправильным балансом 1) Задача с избытком запасов : Вводится фиктивный потребитель. 2) Задача с избытком потребностей(недостаток запасов): 1 ый случай: Вводится фиктивный склад. 2 ой случай: Вводятся весовые коэффициенты. (В ряде случаев может применяться комбинация указанных двух методов. ) 2. Транспортная задача с промежуточными пунктами 3. Транспортная задача с минимизацией времени перевозок

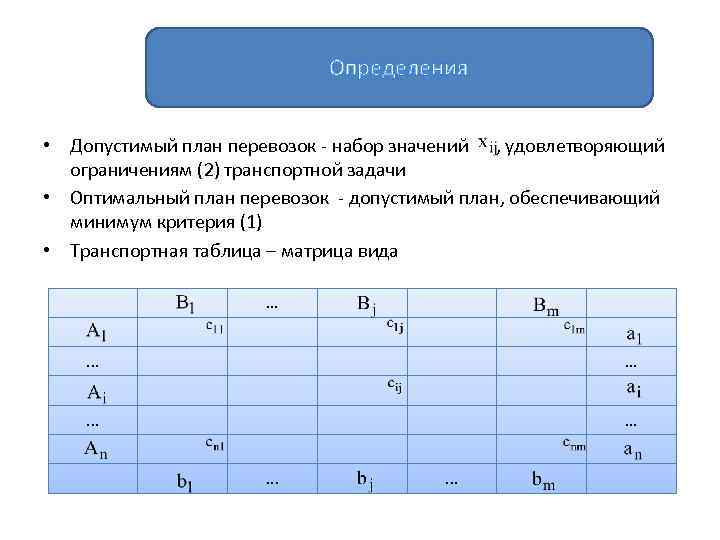Определения • Допустимый план перевозок - набор значений , удовлетворяющий ограничениям (2) транспортной задачи • Оптимальный план перевозок - допустимый план, обеспечивающий минимум критерия (1) • Транспортная таблица – матрица вида …. . . …. . .

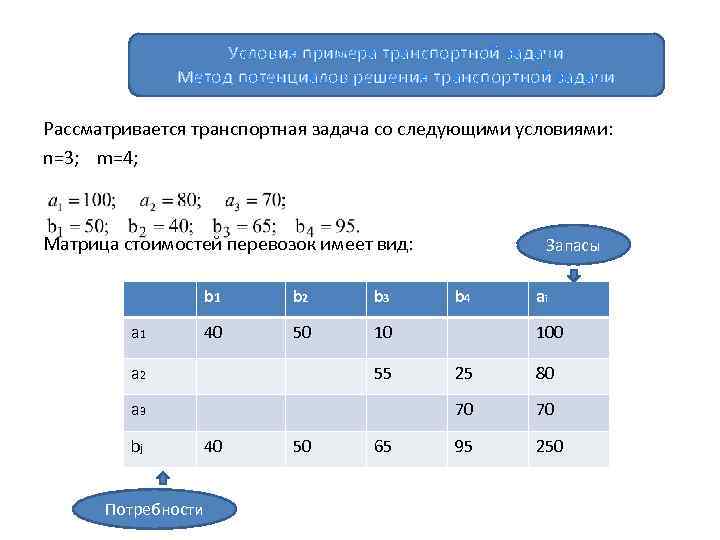Условия примера транспортной задачи Метод потенциалов решения транспортной задачи Рассматривается транспортная задача со следующими условиями: n=3; m=4; Матрица стоимостей перевозок имеет вид: b 1 а 1 b 2 b 3 40 50 10 а 2 55 b 4 ai 100 40 Потребности 50 65 25 80 70 а 3 bj Запасы 70 95 250

Метод северо-западного угла определения начального допустимого плана перевозок Допустимый план перевозок, полученный методом северо-западного угла b 1 a 1 b 2 b 3 40 50 10 a 2 55 ai 100 40 50 65 25 80 70 a 3 bj b 4 70 95 250 Порядок получения плана перевозок методом северо-западного угла: Товары перевозятся из первого склада первому потребителю. Если товаров на первом складе больше, чем надо потребителю, оставшиеся товары направляются второму потребителю и т. д. Если товаров на i-м складе не хватает потребителю, то товары везутся из (i+1)-го склада и т. д. Внимание: оптимальный план содержит n+m-1 ненулевых перевозок (за исключением вырожденных случаев)

План реализации метода северо-западного угла Выполнение начинается с верхней левой ячейки (северо-западного угла) транспортной таблицы. Шаг 1. Переменной х11 присваивается максимальное значение, допускаемое ограничениями на спрос и предложение. Шаг 2. Вычеркивается строка (или столбец) с полностью реализованным предложением (с удовлетворенным спросом). Это означает, что в вычеркнутой строке (столбце) мы не будем присваивать значения остальным неременным (кроме переменной, определенной на первом этапе). Если одновременно удовлетворяются спрос и предложение, вычеркивается только строка или только столбец. Шаг 3. Если не вычеркнута только одна строка или только один столбец, процесс останавливается. В противном случае переходим к ячейке справа, если вычеркнут столбец, или к нижележащей ячейке, если вычеркнута строка. Затем возвращаемся к первому этапу.

Метод Фогеля определения начального допустимого плана перевозок Метод Фогеля. Данный метод является вариацией метода наименьшей стоимости и в общем случае находит лучшее начальное решение. Алгоритм этого метода состоит из следующих шагов. Шаг 1. Для каждой строки (столбца), которой соответствует строго положительное предложение (спрос), вычисляется штраф путем вычитания наименьшей стоимости из следующей по величине стоимости в данной строке (столбце).

Шаг 2. Выделяется строка или столбец с наибольшим штрафом. Если таковых несколько, выбор произволен. Из выделенной строки или столбца выбирается переменная, которой соответствует минимальная стоимость, и ей присваивается наибольшее значение, позволяемое ограничениями. Затем в соответствии с присвоенным значением переменной корректируются величины оставшегося неудовлетворенным спроса и нереализованного предложения. Строка или столбец, соответствующие выполненному ограничению, вычеркиваются из таблицы. Если одновременно выполняются ограничения и по спросу, и по предложению, вычеркивается только строка или только столбец, причем оставшейся строке (столбцу) приписывается нулевое предложение (спрос).

Шаг 3. а) Если не вычеркнута только одна строка или только один столбец с нулевым спросом или предложением, вычисления заканчиваются. б) Если не вычеркнута только одна строка (столбец) с положительным предложением (спросом), в этой строке (столбце) методом наименьшей стоимости находятся базисные переменные, и вычисления заканчиваются. в) Если всем невычеркнутым строкам и столбцам соответствуют нулевые объемы предложения и спроса, методом наименьшей стоимости находятся нулевые базисные переменные, и вычисления заканчиваются. г) Во всех остальных случаях необходимо перейти к п. 1.

Метод потенциалов (псевдостоимостей) решения транспортной задачи

Определение цикла на транспортной таблице Циклом на транспортной таблице называется замкнутая ломаная линия с углами поворота. Примеры циклов: …. . . …. . . Каждой вершине цикла по порядку присваивается признак или. Признак первой вершины определяется произвольно или исходя из требований применяемого для решения задачи алгоритма.

Свойства циклов на транспортной таблице • У любого цикла четное количество вершин • При проходе от вершины к вершине положительнfя и отрицательная вершины чередуются • Ценой цикла называется величина , равная цене перевозки единицы груза, взятой со знаком «+» , если вершина положительна и со знаком «-» , если отрицательна. Рассмотрим цикл 6 8 γ=+8 -6+10 -16=-4 16 10 • При «перемещении» некоторого количества товаров по циклу ограничения транспортной задачи не нарушаются • Для любого допустимого плана перевозок найдется цикл, причем единственный, у которого одна из вершин лежит в свободной клетке таблицы, а все остальные вершины – в клетках транспортной таблицы с ненулевыми перевозками.

Условия оптимальности плана перевозок Для решения задачи методом потенциалов вводится понятие псевдостоимостей: dij = αi + βj, где αi - плата за вывоз единицы груза (i), βj – плата за ввоз j-ому потребителю Для того, чтобы план перевозок был оптимальным необходимо и достаточно, чтобы непустые перевозки псевдостоимости равнялись стоимости перевозок, а для пустых перевозок псевдостоимости были меньше стоимости.

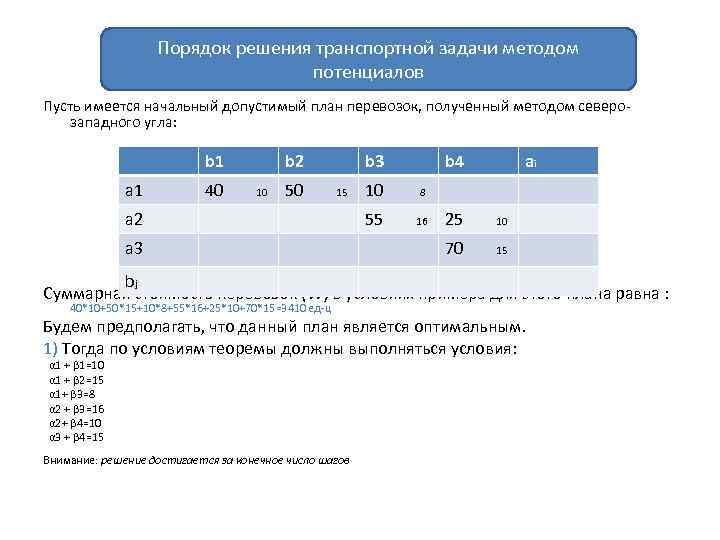Порядок решения транспортной задачи методом потенциалов Пусть имеется начальный допустимый план перевозок, полученный методом северозападного угла: b 1 a 1 40 b 2 10 50 b 3 15 a 2 a 3 b 4 10 8 55 16 ai 25 10 70 15 bj Суммарная стоимость перевозок (W) в условиях примера для этого плана равна : 40*10+50*15+10*8+55*16+25*10+70*15=3410 ед-ц Будем предполагать, что данный план является оптимальным. 1) Тогда по условиям теоремы должны выполняться условия: α 1 + β 1=10 α 1 + β 2=15 α 1+ β 3=8 α 2 + β 3=16 α 2+ β 4=10 α 3 + β 4=15 Внимание: решение достигается за конечное число шагов

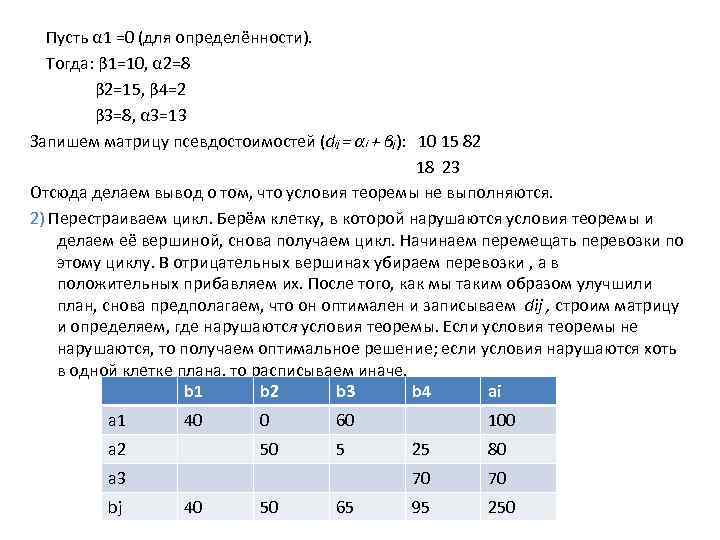Пусть α 1 =0 (для определённости). Тогда: β 1=10, α 2=8 β 2=15, β 4=2 β 3=8, α 3=13 Запишем матрицу псевдостоимостей (dij = αi + βj): 10 15 82 18 23 Отсюда делаем вывод о том, что условия теоремы не выполняются. 2) Перестраиваем цикл. Берём клетку, в которой нарушаются условия теоремы и делаем её вершиной, снова получаем цикл. Начинаем перемещать перевозки по этому циклу. В отрицательных вершинах убираем перевозки , а в положительных прибавляем их. После того, как мы таким образом улучшили план, снова предполагаем, что он оптимален и записываем dij , строим матрицу и определяем, где нарушаются условия теоремы. Если условия теоремы не нарушаются, то получаем оптимальное решение; если условия нарушаются хоть в одной клетке плана, то расписываем иначе. b 1 b 2 b 3 b 4 ai a 1 40 60 50 a 2 0 5 40 50 65 25 80 70 a 3 bj 100 70 95 250

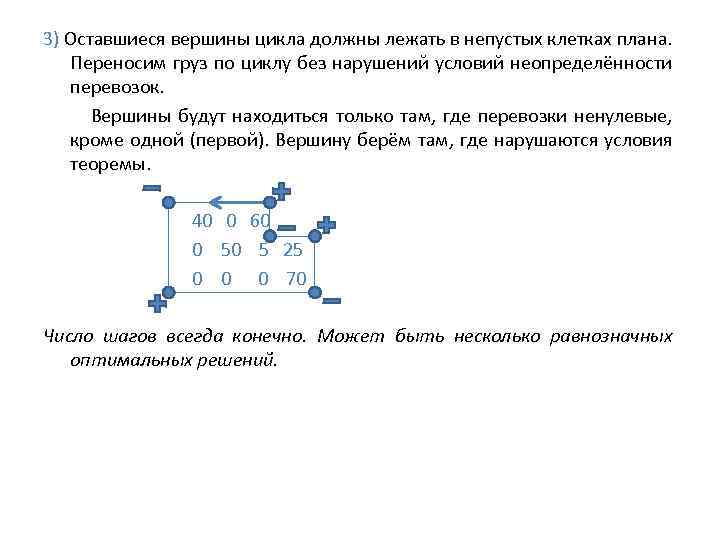3) Оставшиеся вершины цикла должны лежать в непустых клетках плана. Переносим груз по циклу без нарушений условий неопределённости перевозок. Вершины будут находиться только там, где перевозки ненулевые, кроме одной (первой). Вершину берём там, где нарушаются условия теоремы. 40 0 60 0 50 5 25 0 0 0 70 Число шагов всегда конечно. Может быть несколько равнозначных оптимальных решений.

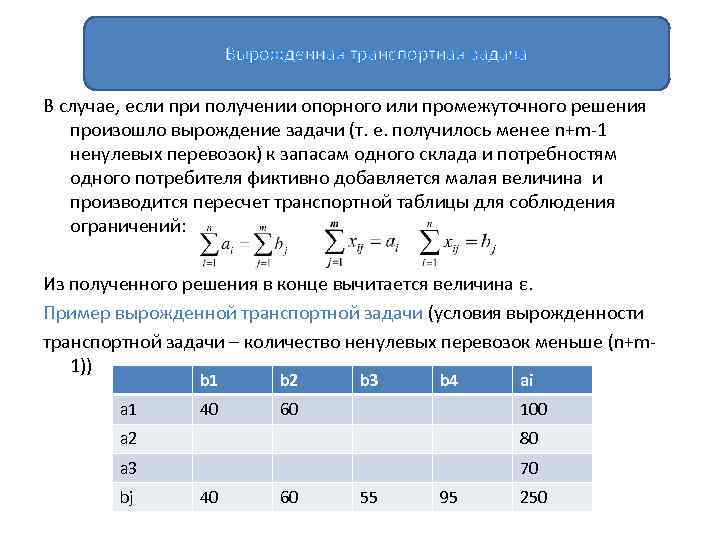Вырожденная транспортная задача В случае, если при получении опорного или промежуточного решения произошло вырождение задачи (т. е. получилось менее n+m-1 ненулевых перевозок) к запасам одного склада и потребностям одного потребителя фиктивно добавляется малая величина и производится пересчет транспортной таблицы для соблюдения ограничений: Из полученного решения в конце вычитается величина ε. Пример вырожденной транспортной задачи (условия вырожденности транспортной задачи – количество ненулевых перевозок меньше (n+m 1)) b 1 a 1 b 2 40 b 3 b 4 60 ai 100 a 2 80 a 3 70 bj 40 60 55 95 250

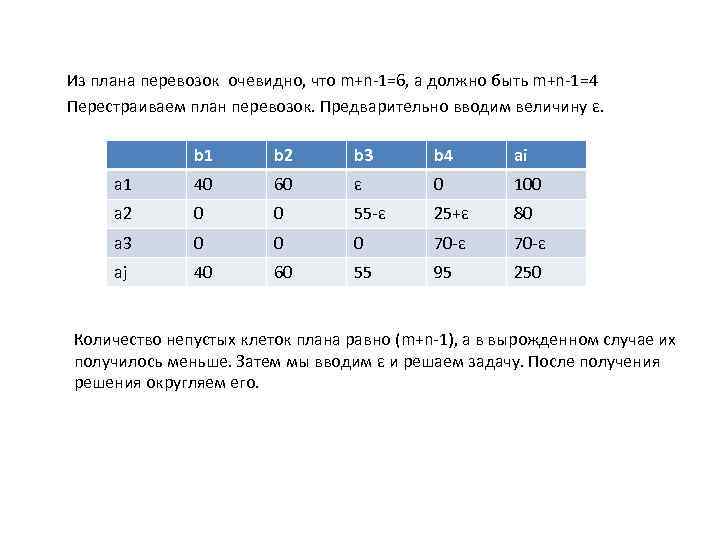Из плана перевозок очевидно, что m+n-1=6, а должно быть m+n-1=4 Перестраиваем план перевозок. Предварительно вводим величину ε. b 1 b 2 b 3 b 4 ai a 1 40 60 ε 0 100 a 2 0 0 55 -ε 25+ε 80 a 3 0 0 0 70 -ε aj 40 60 55 95 250 Количество непустых клеток плана равно (m+n-1), а в вырожденном случае их получилось меньше. Затем мы вводим ε и решаем задачу. После получения решения округляем его.

Обобщения транспортной задачи 1. Транспортные задачи с неправильным балансом Транспортными задачами с неправильным балансом называются транспортные задачи, в которых не выполняется условие: В связи с этим, одно из условий или. Как следствие различают два вида транспортных задач с неправильным балансом: 1) Задача с избытком запасов , когда Для решения такой задачи вводится фиктивный потребитель. Его потребности равны остатку. Нам необходимо знать затраты на перевозки. Затем образуем один столбец и принимаем в нём стоимости перевозок за 0 2) Задача с избытком потребностей(недостаток запасов), когда 1 ый случай: Вводится фиктивный склад. Получаем новую строку с нулевыми стоимостями, так как реально склада не существует. 2 ой случай: Введение весовых коэффициентов. (В ряде случаев может применяться комбинация указанных двух методов. )

2. Транспортная задача с промежуточными пунктами В общем случае при осуществлении перевозок могут возникать ситуации, при которых маршруты перевозок в какие-либо пункты проходят транзитом через другие пункты (через склады или потребителей). Для решения таких задач полагают, что каждый склад является одновременно потребителем, и наоборот – каждый потребитель является одновременно складом, причем через каждый пункт транзитом проходит весь объем товара. Транспортная таблица такой задачи будет иметь n+m строк (складов) и столько же столбцов (потребителей). Запасы на i-ом складе будут равны ai+B, а потребности – В, где Здесь рассматривается задача с правильным балансом. Соответственно потребности каждого потребителя составят bj+B, а запасы – В. Стоимость перевозки товара внутри одного пункта сii равна нулю. После указанных преобразований транспортная задача с промежуточными пунктами является стандартной транспортной задачей и решается существующими методами. Полученные перевозки уменьшаются на В. (Существуют другие алгоритмы сведения транспортной задачи с промежуточными пунктами к стандартной транспортной задаче, обычно учитывающие конкретные особенности существующего множества допустимых маршрутов и, в силу этого, являющиеся более эффективными с вычислительной точки зрения)

3. Транспортная задача с минимизацией времени перевозок Частный случай нелинейных транспортных задач. Имеет вид: Определить X*={xij*}, i=1, …, n, j=1, …, m, такой что: U: • • • Здесь tij – время перевозки продукции с i-ого склада j-ому потребителю. Решение такой задачи также может быть осуществлено методом псевдостоимостей, при этом: в транспортной таблице вместо стоимостей cij используются времена перевозок tij. После получения решения транспортной задачи определяется ненулевая перевозка с максимальной длительностью. Из транспортной таблицы исключается маршрут, соответствующий этой перевозке (для этого время перевозки полагается равным очень большой величине) и задача решается заново. Этот процесс повторяется до тех пор, пока при переходе к последующему решению не произойдет увеличение длительности самой долгой перевозки в полученном оптимальном решении.

4. Обобщение, связанное с ограничениями на пропускную способность маршрутов С точки зрения формализации в задаче появляются дополнительные ограничения: Задача линейного программирования позволяет использовать ограничения любого вида. Достаточно ввести на каждом шаге проверку по всем вершинам цикла.

5. Сезонные изменения Имеют место сезонные изменения спроса, связанные с ограничениями на время года. Колебания спроса напрямую влияют на объём выпуска. 6. Многопродуктовая сеть 7. Фиксированный объём транспортных средств 8. Задача о назначениях "Лучший работник для выполнения данной работы" — вот подходящее краткое описание задачи о назначениях. В этой задаче необходимо назначить работников на определенные работы; каждый работник может выполнять любую работу, хотя и с различной степенью мастерства. Если на некоторую работу назначается работник именно той квалификации, которая необходима для ее выполнения, тогда стоимость выполнения работы будет ниже, чем при назначении на данную работу работника неподходящей квалификации. Цель задачи — найти оптимальное (минимальной стоимости) распределение работников по всем заявленным работам. Существуют специальные алгоритмы решения задач о назначениях. Можно использовать избыток запасов и исполнителей (т. е. решать как вырожденную задачу, взяв ε=0. 0001)

Задача о минимальном покрытии Относится к сетевым задачам Техническая постановка: Имеется n пунктов, которые все должны быть связаны дорожной сетью. Расстояние между пунктами известно. Определить: Такую структуру дорожной сети, чтобы суммарная длина дорог была минимальна. С математической точки зрения: Имеется граф с известными длинами рёбер. Требуется найти дерево-остов данного графа с минимальной суммарной длиной рёбер. (дерево-остов – минимальный связный подграф данного графа) Формализованная постановка задачи: Есть N пунктов и расстояния между ними Cij. W= Ограничения: Cij=0; k=

Задача о кратчайшем маршруте Техническая постановка: Имеется 2 пункта, связанных между собой дорожной сетью, проходящей ещё через какие-либо пункты. Длины дорог между любыми пунктами известны. Требуется определить кратчайший маршрут между указанными двумя пунктами. Математическая постановка: имеется граф с заданной длиной всех рёбер. Требуется на графе определить цепь, связывающую все заданные вершины и имеющую минимально возможную длину. Условие: все ребра имеют неотрицательную длину.

Алгоритм решения задачи о кратчайшем маршруте При решении задачи о кратчайшем маршруте различаются два класса задач: задачи без циклов и задачи с циклами. В задачах без циклов нельзя вернуться в ранее покинутый пункт, в задачах с циклами могут существовать совокупности связанных дорог, по которым можно вернуться в ранее покинутый пункт. Для реальных транспортных сетей характерными являются задачи с циклами. Задачи без циклов обычно возникают при формализации задач о нахождении минимальных сроков каких – либо последовательностей работ в виде задачи о кратчайшем маршруте. Если длина ребра = 1, удобно использовать волновой алгоритм. Берём начальную точку маршрута и «запускаем волну» , т. е. выбираем точки, которых можно достичь из данной. Далее каждую точку рассматриваем как источник новой «волны» . Как только фронт «волны» достиг нужной точки, получен кратчайший маршрут.

Алгоритм определения кратчайшего маршрута при неединичных длинах рёбер Для сетей без цикла Можно считать, что исходный пункт является первым, а пункт назначения – последним, т. е. , что а=1 и b=I. uj – кратчайшее расстояние между первым и j-ым пунктами; dij – расстояние между смежными пунктами с номерами i и j; Для всех последовательно вычислить Кратчайший маршрут определяется величиной uj.

Сведение задачи о кратчайшем маршруте к задаче линейного программирования Если вместо расстояния положим стоимость, то это напоминает транспортную задачу с промежуточными пунктами. Можно сказать, что перевозим единицу груза из первого пункта в последний при минимальной суммарной длине маршрута. Формально: , если путь vij входит в кратчайший маршрут в противном случае.

Задача о максимальном потоке Классическая постановка задачи о максимальном потоке имеет вид: Имеется I пунктов еi, соединенных дорогами vij с пропускными способностями сij. Требуется определить максимальный суммарный поток, проходящий из исходного пункта es в конечный пункт et. Можно считать, что исходный пункт является первым, а конечный пункт – последним. Метод сечения (метод разрезов) Разрезом на связном графе называется множество рёбер, удаление которых превращает граф в 2 несвязных подграфа (т. е. источник и исток оказываются в разных подграфах). Максимальным является поток, который минимален из всех по объёму товара, который можно передать из исходного пункта в конечный.

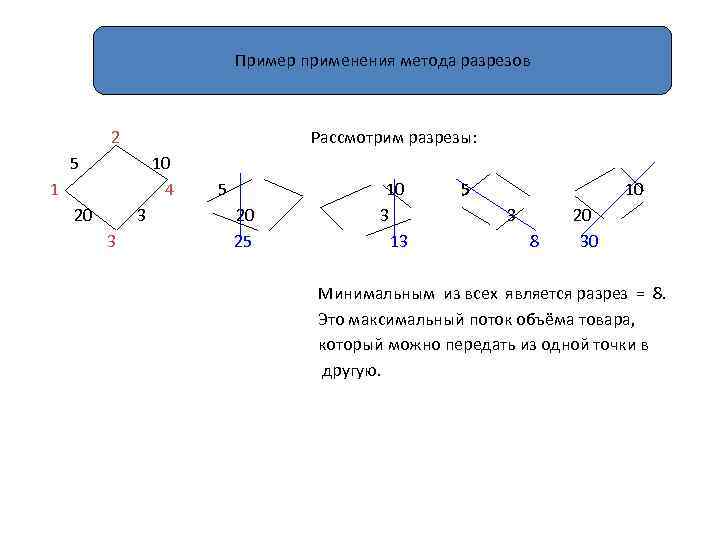Пример применения метода разрезов 2 Рассмотрим разрезы: 5 10 4 1 20 3 3 5 20 25 10 3 13 5 10 3 8 20 30 Минимальным из всех является разрез = 8. Это максимальный поток объёма товара, который можно передать из одной точки в другую.

Сведение задачи о максимальном потоке к задаче линейного программирования Максимальный поток в направлении равен z, где ограничения: входящий поток = исходящему Xij – объём товара, перемещаемый от вершины ik к вершине j.

Задача о формировании сети минимальной стоимости Данную задачу в обобщённой постановке можно свести к Вышеуказанным задачам. Относится к классу сетевых задач, следовательно можно свести к задаче линейного программирования.

Сетевое планирование – математические методы управления проектами (сложными комплексами работ). Сетевое планирование подразумевает следующее: 1) Формируется перечень работ Используем вертикально-горизонтальную структуру. При этом возможен внутренний обмен информацией и использование разработок в других проектах. 2) Определение временной зависимости между работами 3) Упорядочение работ (ранжирование)

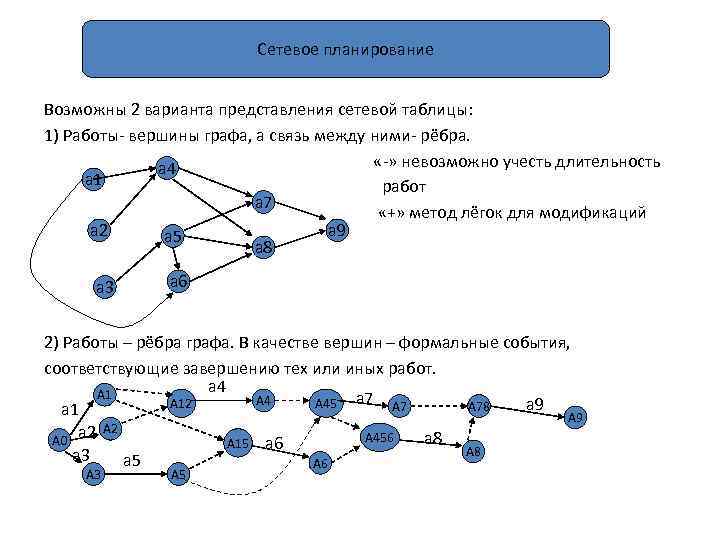Сетевое планирование Возможны 2 варианта представления сетевой таблицы: 1) Работы- вершины графа, а связь между ними- рёбра. «-» невозможно учесть длительность а 4 а 1 работ а 7 «+» метод лёгок для модификаций а 2 а 9 а 5 а 8 а 3 а 6 2) Работы – рёбра графа. В качестве вершин – формальные события, соответствующие завершению тех или иных работ. а 4 А 1 А 4 А 12 А 45 а 7 А 7 а 9 А 78 а 1 А 9 А 2 А 456 а 8 А 0 а 2 А 15 а 6 А 8 а 3 а 5 А 6 А 3 А 5

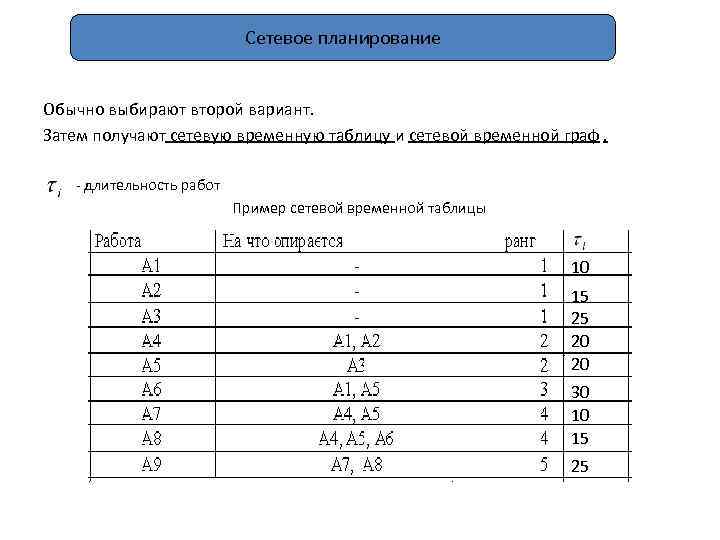Сетевое планирование Обычно выбирают второй вариант. Затем получают сетевую временную таблицу и сетевой временной граф. - длительность работ Пример сетевой временной таблицы 10 15 25 20 20 30 10 15 25

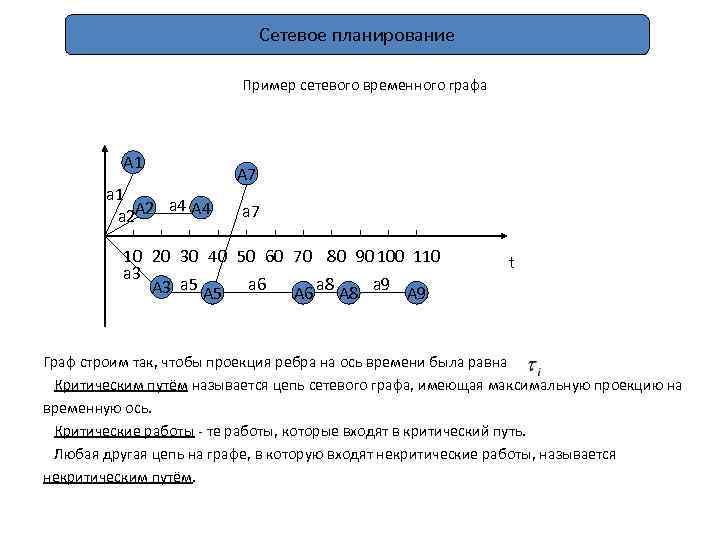Сетевое планирование Пример сетевого временного графа A 1 а 4 A 4 а 2 A 2 А 7 а 7 10 20 30 40 50 60 70 80 90 100 110 а 3 А 3 а 5 А 5 а 6 А 6 а 8 А 8 а 9 А 9 t Граф строим так, чтобы проекция ребра на ось времени была равна Критическим путём называется цепь сетевого графа, имеющая максимальную проекцию на временную ось. Критические работы - те работы, которые входят в критический путь. Любая другая цепь на графе, в которую входят некритические работы, называется некритическим путём.

Основные постановки задач сетевого планирования 1 постановка Основное условие Ткр > Ттреб (не успеваем в сроки). Чтобы решить данную задачу, необходимо знать, сколько стоит изменение времени выполнения работы. Существует функция, связывающая с (дополнительные ресурсы, которые нужно внести). Формальная постановка задачи: Ограничение: . Критерий: Алгоритм решения 1. Сокращение критических работ 2. Введение обобщённого ресурса

Основные постановки задач сетевого планирования 2 постановка Условие: , (т. е. в рамках существующих ресурсов мы должны сократить время выполнения проекта). 3 постановка При необходимо

Направления в области управления проектами 1) Параллельное выполнение проектов. При этом ограниченный ресурс перераспределяют между проектами, происходит смещение работ, накладываются дополнительные условия. 2) - случайная величина (неопределённый срок выполнения операции). Используют PERT- метод (эвристический подход). Для каждой работы производятся 3 оценки : -при наиболее благоприятных условиях - наиболее вероятное - при наиболее неблагоприятных условиях. Ткр( , )=Тmin Ткр( , )=Тожид Ткр( , )=Тmax Ткр=

Теория расписаний Относится к классу сетевых задач. Теория расписаний занимается распределением комплекса работ по разным исполнителям или последовательностью выполнения различных работ. 2 основные постановки задач: 1) Задача о мультипроцессоре 2) Задача о выборе последовательности выполнения работ

Задача о мультипроцессоре Имеется k процессоров, n работ, каждая из работ длится - длительность перехода от i-ой работы к j-ой на k-ом виде процессора. Tmax- время выполнения всех работ. Критерий: Tmax min Если =0 или =const, то необходимо перераспределить работы между процессорами. Если 0, то необходимо выяснить порядок выполнения работ. Быстрее всего работы будут выполнены, если их равномерно распределить между процессорами. Но длительность работ дискретна и не всегда удаётся идеально распределить работы. Поэтому необходимо использовать среднее время выполнения работ процессором. - среднее время выполнения работы процессором. k - количество процессоров Данная задача является нелинейной, т. е. нет универсального метода решения, кроме метода перебора.

Задача о выборе последовательности работ Имеется k обрабатывающих линий. Каждая линия выполняет свои специфические операции. Необходимо определить последовательность обработки объектов, чтобы суммарное время обработки было минимальным. Решение производят с помощью теоремы Джонсона для двух станков в линейной постановке. В других случаях общего решения нет.