Сеть представляется в виде конечного Связного орграфа G V

Сеть представляется в виде конечного Связного орграфа G(V, E) без петель, каждой дуге которого поставлено в соответствие некоторое неотрицательное число , называемое пропускной способностью C(e) дуги, и в котором существуют один источник и один сток Источник – вершина. V 0=S , в которую не заходит ни одна дуга Сток - вершина Vn=T, из которой не выходит ни одной дуги

Потоком сети называется неотрицательная функция f такая, что f(e) меньше или равно (Поток не может превышать пропускную способность дуги. ). Дуга называется насыщенной потоком, если поток через эту дугу равен пропускной способности дуги f(e)=

Величина максимального потока из равна величине минимального разреза( отделяющего S от T. Разрез( ), отделяет S от T, если: Величиной такого разреза называется сумма пропускных способностей всех дуг, начальные вершины которых лежат в ( ), а конечные в ( ).

Алгоритм начинает работу с произвольного допустимого потока (можно взять и нулевой поток), затем стремится увеличить его с помощью систематического поиска всех возможных аргументальных цепей (тех, которые можно увеличить) потока от S к T. Поиск таких цепей осуществляется с помощью расстановки пометок в вершинах графа. Пометка указывает вдоль каких дуг может быть увеличен поток и на сколько. Как только найдена одна из таких цепей, поток вдоль неё увеличивают до максимального значения, а пометки в вершинах стираются, и вновь полученный поток используется в качестве исходного при новой расстановке пометок. Алгоритм завершает работу, когда нельзя найти ни одной аргументальной цепи.

Вершина может находиться в одном из трех состояний: 1. Вершина просмотрена и ей приписана пометка (Она имеет пометку и все смежные с ней вершины обработаны. ). 2. Вершина помечена, но не просмотрена(Она имеет пометку, но смежные с ней вершины не обработаны. ). 3. Вершина не имеет пометок.

Пометка произвольной вершины состоит из двух частей: Часть « » означает, что поток допускает увеличение вдоль дуги. « » задает максимальную величину дополнительного потока, который протекает от S к вдоль построенной аргументальной цепи потока.

Процедура нахождения максимального потока состоит из трех пунктов: 1. Вершине S присвоить пометку 2. Каждой непомеченной ненасыщенной вершине 3. инцидентной предыдущей вершине присвоить пометку , где 4. 3. Пункт 2 повторяется пока либо будет помечена вершина Т(В этом случае возвращаемся к стоку и начинаем алгоритм заново учитывая насыщенные дуги), либо пока никаких других пометок нельзя будет поставить(В этом случае полученный поток является максимальным)

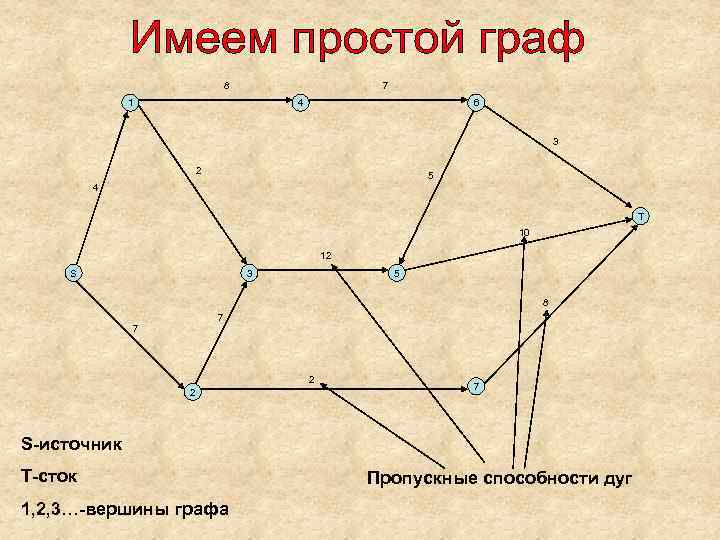8 7 1 4 6 3 2 5 4 T 10 12 S 3 5 8 7 7 2 2 7 S-источник T-сток 1, 2, 3…-вершины графа Пропускные способности дуг

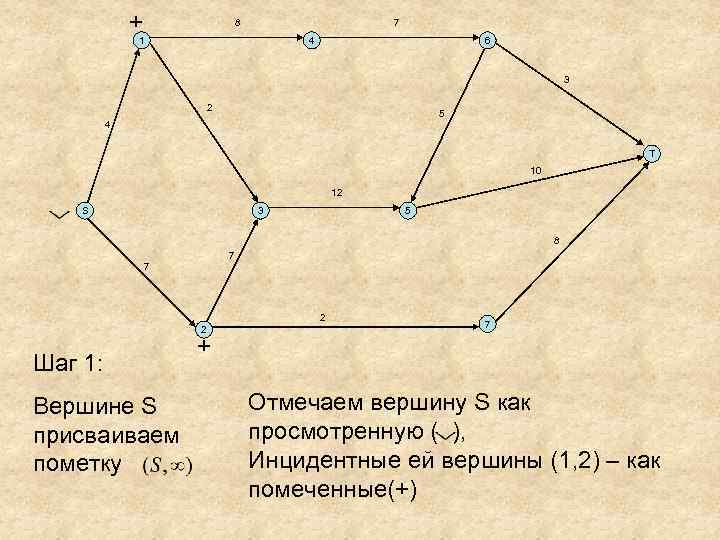+ 8 7 1 4 6 3 2 5 4 T 10 12 S 3 5 8 7 7 2 2 Шаг 1: Вершине S присваиваем пометку 7 + Отмечаем вершину S как просмотренную ( ), Инцидентные ей вершины (1, 2) – как помеченные(+)

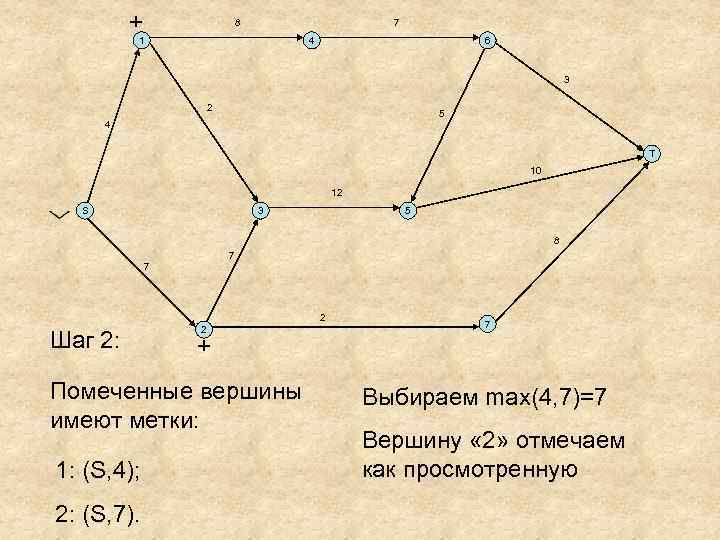+ 8 7 1 4 6 3 2 5 4 T 10 12 S 3 5 8 7 7 2 Шаг 2: 2 + Помеченные вершины имеют метки: 1: (S, 4); 2: (S, 7). 7 Выбираем max(4, 7)=7 Вершину « 2» отмечаем как просмотренную

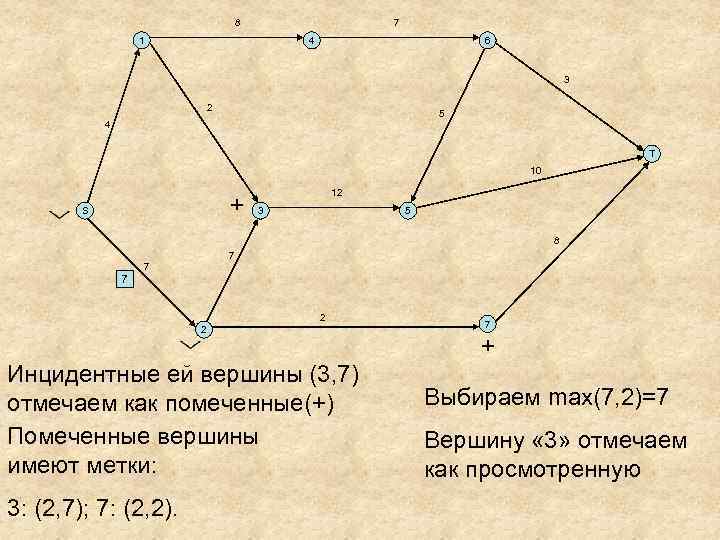8 7 1 4 6 3 2 5 4 T 10 + S 12 3 5 8 7 7 7 2 2 Инцидентные ей вершины (3, 7) отмечаем как помеченные(+) Помеченные вершины имеют метки: 3: (2, 7); 7: (2, 2). 7 + Выбираем max(7, 2)=7 Вершину « 3» отмечаем как просмотренную

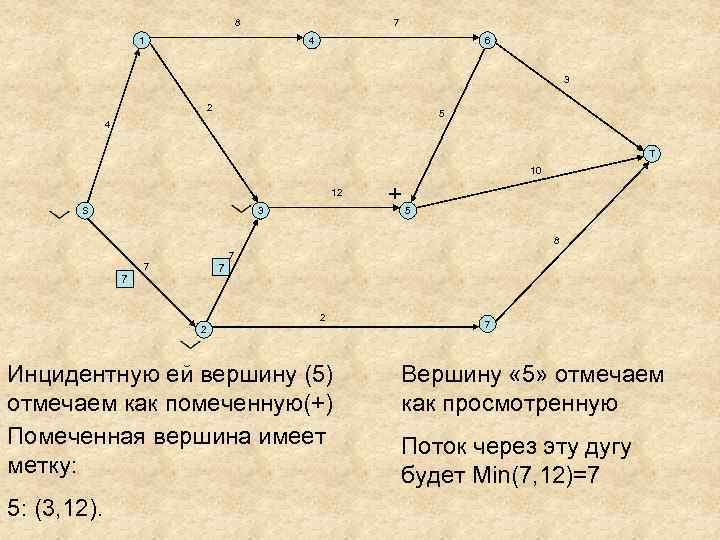8 7 1 4 6 3 2 5 4 T 10 12 S 3 + 5 8 7 7 2 2 Инцидентную ей вершину (5) отмечаем как помеченную(+) Помеченная вершина имеет метку: 5: (3, 12). 7 Вершину « 5» отмечаем как просмотренную Поток через эту дугу будет Min(7, 12)=7

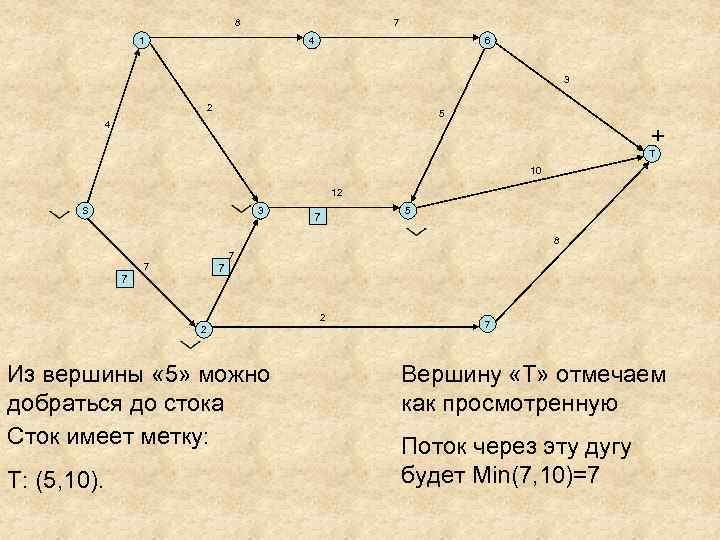8 7 1 4 6 3 2 5 4 + T 10 12 S 3 7 5 8 7 7 2 2 Из вершины « 5» можно добраться до стока Сток имеет метку: Т: (5, 10). 7 Вершину «T» отмечаем как просмотренную Поток через эту дугу будет Min(7, 10)=7

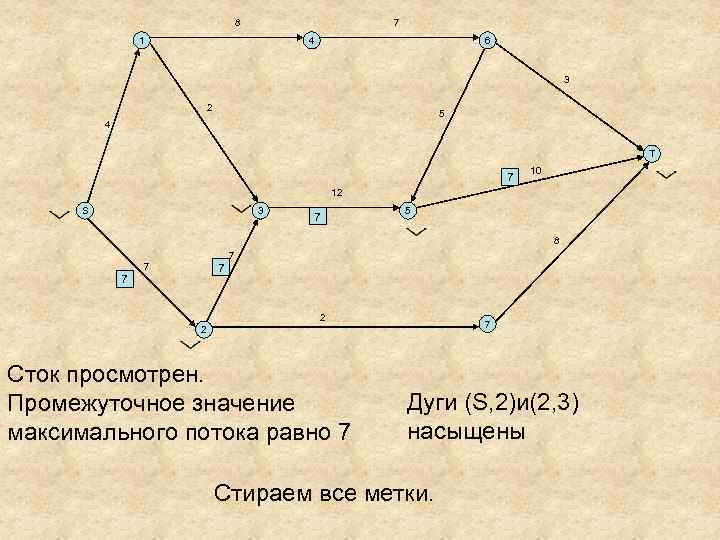8 7 1 4 6 3 2 5 4 T 7 10 12 S 3 7 5 8 7 7 2 7 2 Сток просмотрен. Промежуточное значение максимального потока равно 7 Дуги (S, 2)и(2, 3) насыщены Стираем все метки.

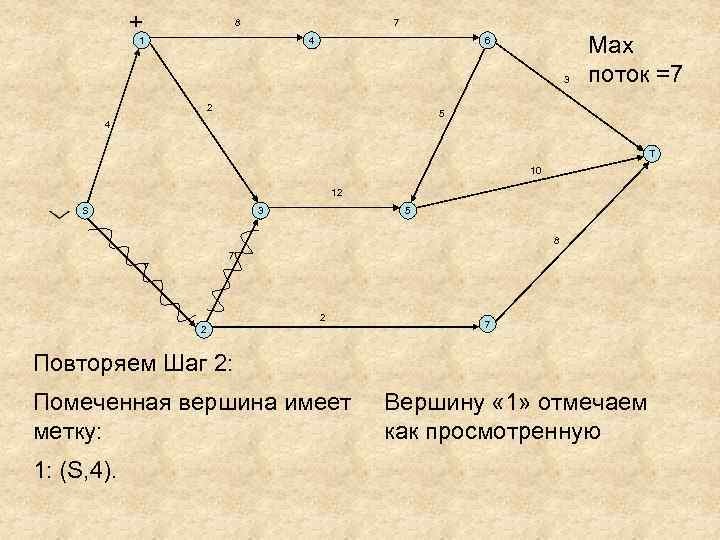+ 8 7 1 4 6 3 2 Мах поток =7 5 4 T 10 12 S 3 5 8 7 7 2 2 7 Повторяем Шаг 2: Помеченная вершина имеет метку: 1: (S, 4). Вершину « 1» отмечаем как просмотренную

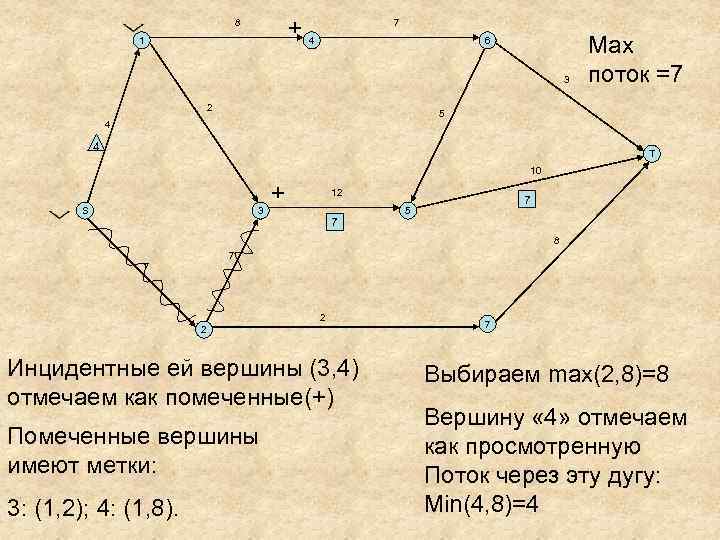+4 8 1 7 6 3 2 Мах поток =7 5 4 4 T 10 S 3 + 12 7 7 5 8 7 7 2 2 Инцидентные ей вершины (3, 4) отмечаем как помеченные(+) Помеченные вершины имеют метки: 3: (1, 2); 4: (1, 8). 7 Выбираем max(2, 8)=8 Вершину « 4» отмечаем как просмотренную Поток через эту дугу: Min(4, 8)=4

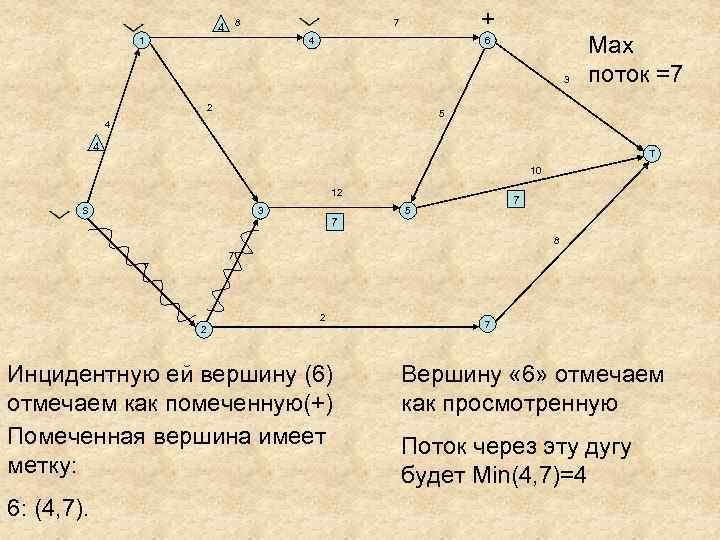4 8 + 7 1 4 6 3 2 Мах поток =7 5 4 4 T 10 12 S 3 7 7 5 8 7 7 2 2 Инцидентную ей вершину (6) отмечаем как помеченную(+) Помеченная вершина имеет метку: 6: (4, 7). 7 Вершину « 6» отмечаем как просмотренную Поток через эту дугу будет Min(4, 7)=4

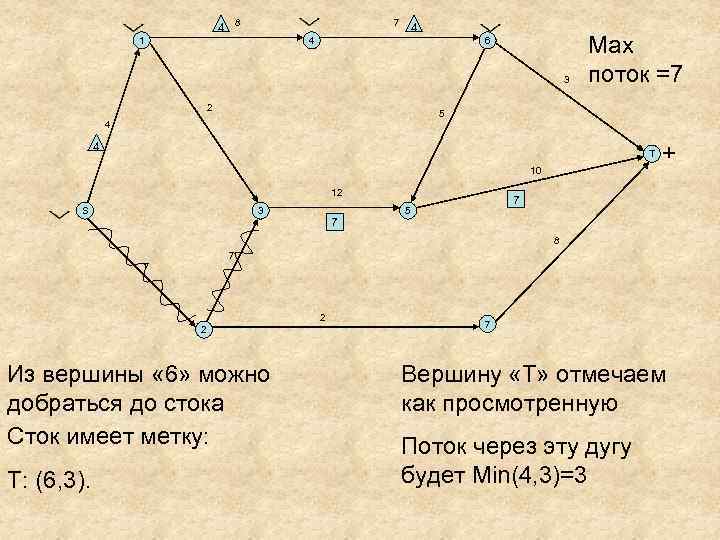4 8 7 1 4 4 6 3 2 Мах поток =7 5 4 4 T 10 12 S 3 7 + 7 5 8 7 7 2 2 Из вершины « 6» можно добраться до стока Сток имеет метку: Т: (6, 3). 7 Вершину «T» отмечаем как просмотренную Поток через эту дугу будет Min(4, 3)=3

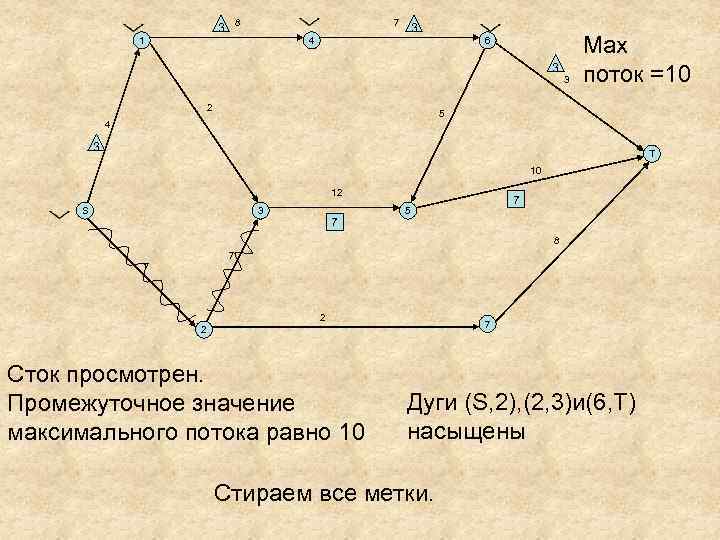3 8 7 1 3 4 6 3 2 3 Мах поток =10 5 4 3 T 10 12 S 3 7 7 5 8 7 7 2 Сток просмотрен. Промежуточное значение максимального потока равно 10 Дуги (S, 2), (2, 3)и(6, Т) насыщены Стираем все метки.

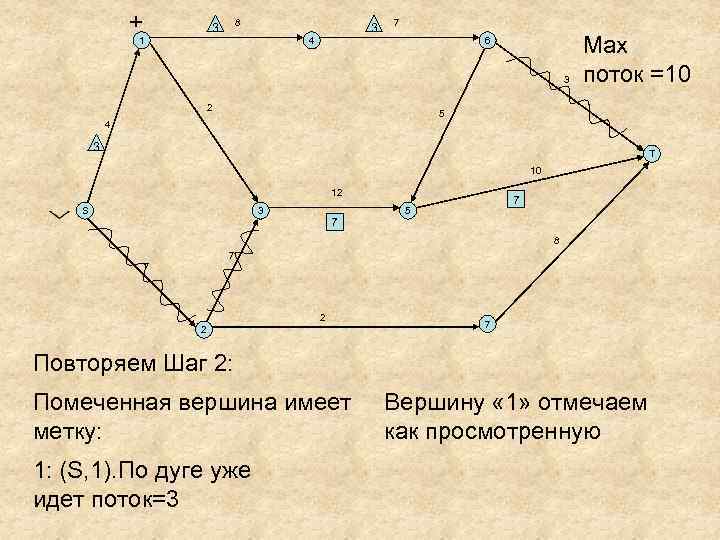+ 8 3 3 1 7 4 6 3 2 Мах поток =10 5 4 3 T 10 12 S 3 7 7 5 8 7 7 2 2 7 Повторяем Шаг 2: Помеченная вершина имеет метку: 1: (S, 1). По дуге уже идет поток=3 Вершину « 1» отмечаем как просмотренную

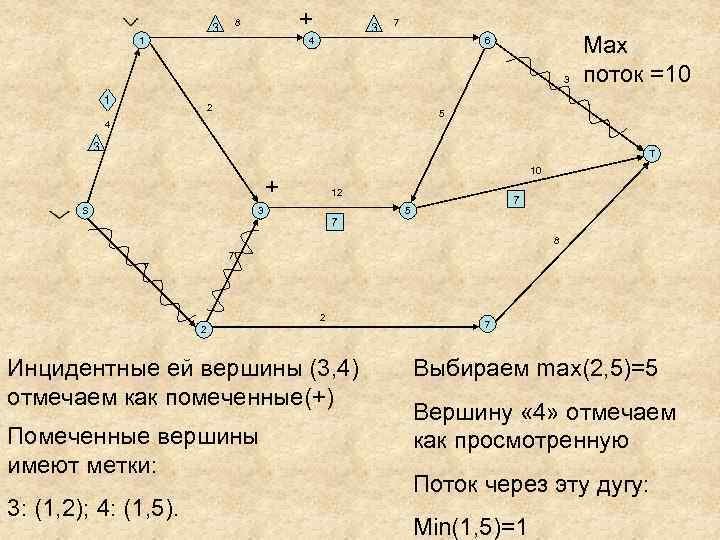+ 8 3 1 3 7 4 6 3 1 2 Мах поток =10 5 4 3 T 10 + S 12 3 7 7 5 8 7 7 2 2 Инцидентные ей вершины (3, 4) отмечаем как помеченные(+) Помеченные вершины имеют метки: 3: (1, 2); 4: (1, 5). 7 Выбираем max(2, 5)=5 Вершину « 4» отмечаем как просмотренную Поток через эту дугу: Min(1, 5)=1

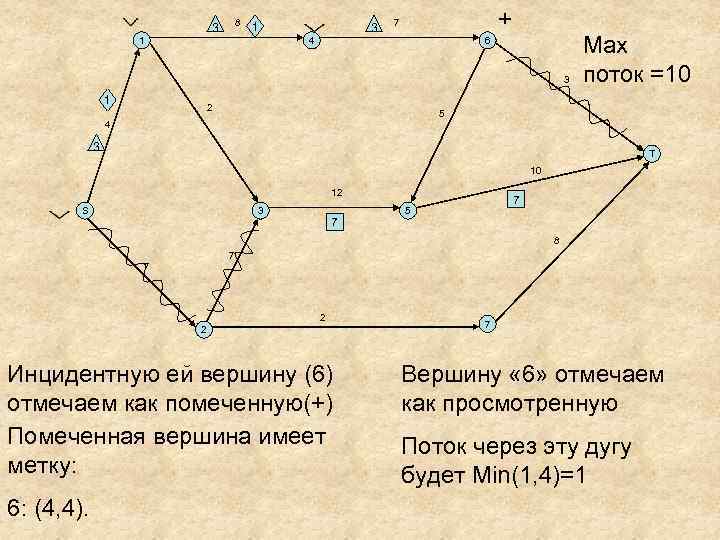8 3 1 1 3 + 7 4 6 3 1 2 Мах поток =10 5 4 3 T 10 12 S 3 7 7 5 8 7 7 2 2 Инцидентную ей вершину (6) отмечаем как помеченную(+) Помеченная вершина имеет метку: 6: (4, 4). 7 Вершину « 6» отмечаем как просмотренную Поток через эту дугу будет Min(1, 4)=1

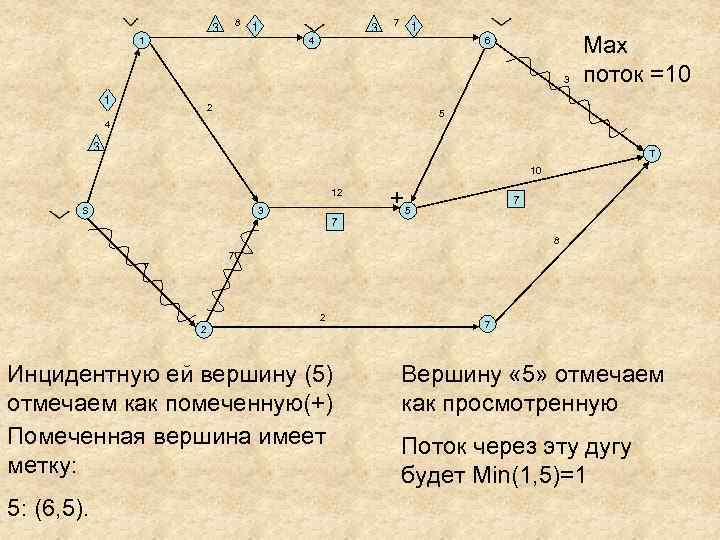8 3 1 1 3 7 1 4 6 3 1 2 Мах поток =10 5 4 3 T 10 12 S 3 7 +5 7 8 7 7 2 2 Инцидентную ей вершину (5) отмечаем как помеченную(+) Помеченная вершина имеет метку: 5: (6, 5). 7 Вершину « 5» отмечаем как просмотренную Поток через эту дугу будет Min(1, 5)=1

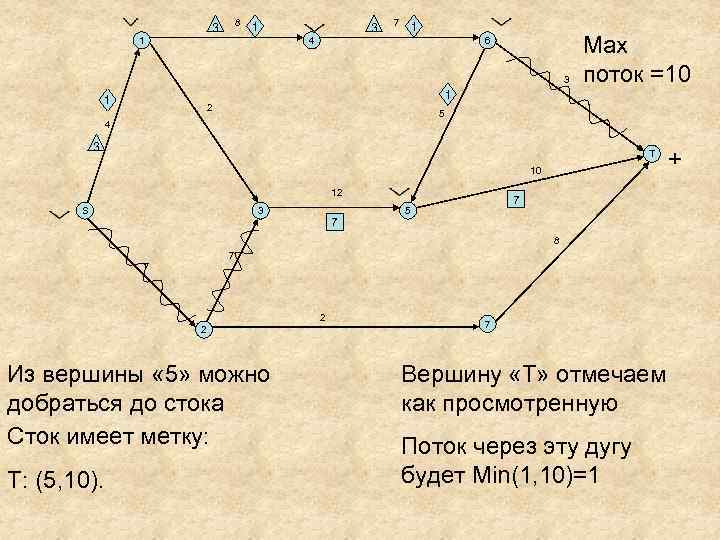8 3 1 1 3 7 1 4 6 3 Мах поток =10 1 1 2 5 4 3 T 10 12 S 3 7 7 5 8 7 7 2 2 Из вершины « 5» можно добраться до стока Сток имеет метку: Т: (5, 10). 7 Вершину «T» отмечаем как просмотренную Поток через эту дугу будет Min(1, 10)=1 +

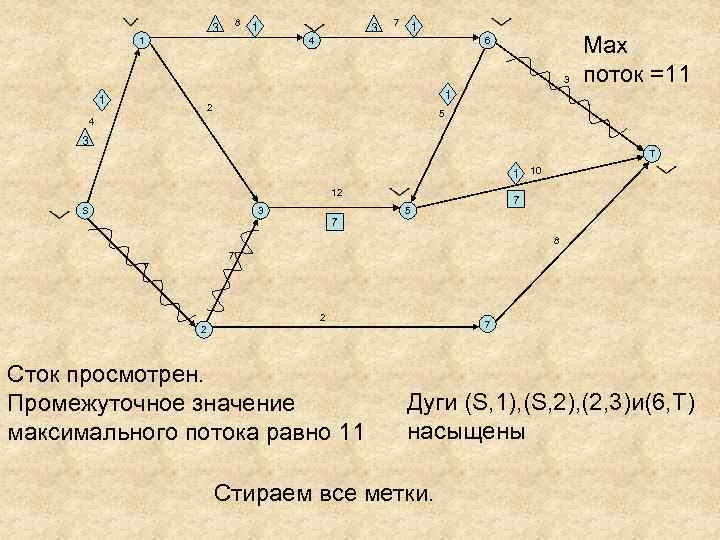8 3 1 1 3 7 1 4 6 3 Мах поток =11 1 1 2 5 4 3 T 1 10 12 S 3 7 7 5 8 7 7 2 Сток просмотрен. Промежуточное значение максимального потока равно 11 Дуги (S, 1), (S, 2), (2, 3)и(6, Т) насыщены Стираем все метки.

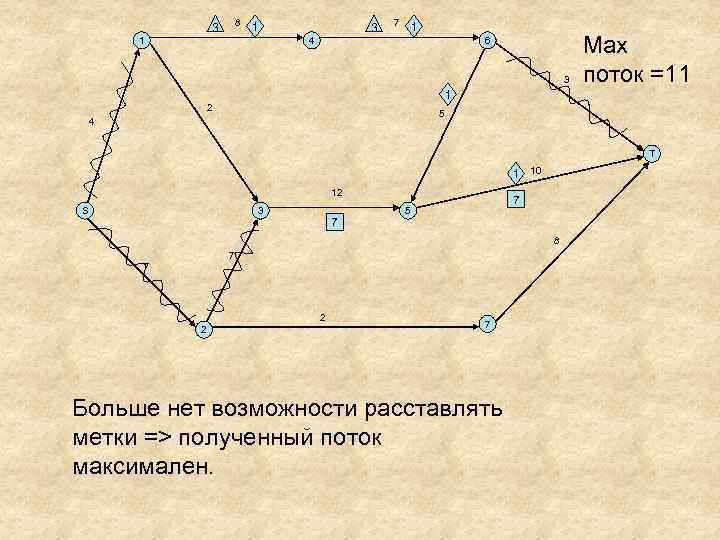8 3 1 1 3 7 1 4 6 3 Мах поток =11 1 2 5 4 T 1 10 12 S 3 7 7 5 8 7 7 2 2 7 Больше нет возможности расставлять метки => полученный поток максимален.