Серия учебных мультимедийных пособий О В Гурьева Рисунки

Серия учебных мультимедийных пособий О. В. Гурьева Рисунки Галилея, иллюстрирующие рассуждения о сопротивлении материалов Для студентов средних профессиональных образовательных учреждений очной формы обучений. Часть 2. по разделу «Сопротивлению материалов»

ЦЕЛЬ УРОКА Повторить и обобщить понятий характерных для всех деформаций Вывести основных положений характерных для деформаций срез и смятие. Решить задачу на срез и смятие.

Система оценивания 5 правильных ответов - 5 4 правильных ответов – 4 3 правильных ответов - 3 ОТВЕТЫ • 1 вариант 1 - 2 • 2 -1 • 3 -1 • 4 -1 • 5 -1 2 Вариант 1 -3 2 -1 3 -3 4 -2 5 -2

Срезом (сдвигом) называется деформация, возникающая под действием двух близко расположенных противоположно направленных равных сил. При этом возникают касательные напряжения. ПРИМЕР: заклепка (заклепочное соединение). При некоторой величине действующих сил F стержень заклепки может быть срезан по сечению. Силы F передаются путем давления стенок отверстия на стержень заклепки. При большом давлении может произойти значительное смятие стенок отверстия или стержня заклепки по поверхности их соприкосновения.

Смятием называется местная деформация сжатия по площадкам передачи давления. Возникающие нормальные напряжения смятия являются местными. Чтобы найти напряжения, возникающие в сечении стержня заклепки под действием сил F, применим метод сечений. Рассечем мысленно стержень заклепки на две части.

Вопрос 1. Назовите простейшие виды внешних нагрузок (ВШС) и их единицы измерения. Активные Реактивные F (указать виды опор, и их реакции) P A F, Рm B mg L С е Q g Q

Ответ на вопрос 1. Назовите простейшие виды внешних нагрузок (ВШС) и их единицы измерения. Активные Реактивные F (указать виды опор, и их реакции) P RA Шарнирно-подвижная опора A Реакция направлена перпендикулярно опорной плоскости F, Р- Сосредоточенные силы, Н, к. Н m m RBY или Шарнирно-неподвижная опора B Реакции направлены RBX перпендикулярно оси шарнира; её изображают в виде двух составляющих RBY, RBX m- Момент пары сил, Нм g L Q Равномерно – распределённая нагрузка Жесткая заделка (защемление) RC RСY g -интенсивность равномерно - С распределённой нагрузки, н/м Q -сосредоточенная сила, приложенная в центре участка Q=q. L действия нагрузки, Н RСX MC В опоре С возникают реактивный момент Мс и реакция Rc, которую заменяют двумя составляющими Rcx, Rcy

Вопрос 2. Под действием внешних нагрузок (ВШС) внутри бруса возникают внутренние силовые факторы (ВСФ) Какой метод применяется для определения внутренних силовых факторов (ВСФ), возникающих под действием внешних нагрузок и в чем он заключается?

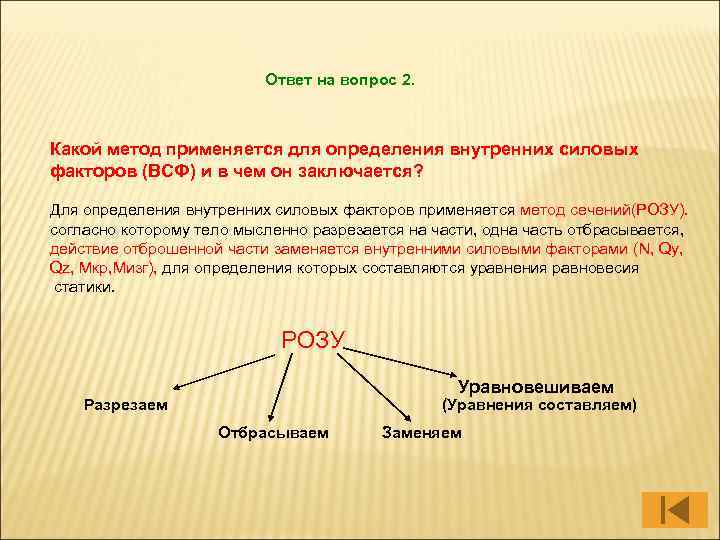
Ответ на вопрос 2. Какой метод применяется для определения внутренних силовых факторов (ВСФ) и в чем он заключается? Для определения внутренних силовых факторов применяется метод сечений(РОЗУ). согласно которому тело мысленно разрезается на части, одна часть отбрасывается, действие отброшенной части заменяется внутренними силовыми факторами (N, Qy, Qz, Mкр, Мизг), для определения которых составляются уравнения равновесия статики. РОЗУ Уравновешиваем Разрезаем (Уравнения составляем) Отбрасываем Заменяем

Вопрос 3. Какие ВСФ возникают в сечении детали под действием ВШС? N Qyy My F Qz- мх N My- Qz x Qy P Mz- мх Mz z

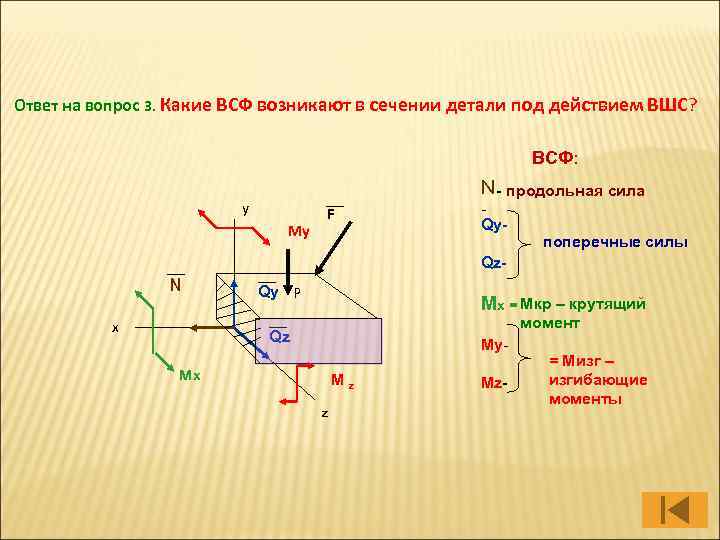
Ответ на вопрос 3. Какие ВСФ возникают в сечении детали под действием ВШС? ВСФ: N - продольная сила y My F Qy- поперечные силы Qz- N x Qy P Мх = Мкр – крутящий момент Qz My- мх Mz z Mz- = Мизг – изгибающие моменты

Вопрос 4. Прочитайте формулу: ВСФ= ∑ВШС Как определить модуль и знак ВСФ? N= Qy= Qz= Mx=Мкр My=Мизг Mz=Мизг

Ответ на вопрос 4. Прочитайте формулу: ВСФ= ∑ВШС? Как определить модуль и знак ВСФ? ВСФ= ∑ ВШС -внутренний силовой фактор в сечении бруса равен алгебраической сумме внешних сил, действующих на оставшуюся часть бруса ∑ Мс- алгебраическая сумма моментов внешних сил ∑ Fix, ∑ Fiy, ∑ Fiz-алгебраические суммы проекций внешних сил на оси координат относительно центра проведённого сечения ∑ Tix - алгебраическая сумма моментов внешних сил относительно оси х Модуль ВСФ Знак «+» Знак «-» Qy=∑Fiy Qz=∑Fiz N=∑Fix F N F Mкр= =∑Tix М или Т Q Мкр F F N М Мизг F М или Т Мкр М М F F М Условно F Q Mизг= =∑Mc(F) Условно Мизг

Вопрос 5. Какие ВСФ возникают в детали и какие деформации они при этом испытывают при a) различных способах нагружения? F F в) F F г) б) F F F

Ответ на вопросы 5. Какие ВСФ возникают в детали и какие деформации они при этом испытывают при различных способах нагружения? F F в) a) F N N N ≠ 0, (смятие- местная деформация сжатия) F N ≠ 0 -растяжение г) б) F F F N Q N ≠ 0 - сжатие F F Q ≠ 0 - сдвиг (срезсдвиг доведённый до разрушения)

Вопрос 6. Что такое механическое напряжение? Его единицы измерения? Вопрос 7. Укажите виды механических напряжений в зависимости от направления по отношению к поперечному сечению тела. m F g

Ответы на вопросы 6, 7 Что такое механическое напряжение? Его единицы измерения? Укажите виды механических напряжений в зависимости от направления по отношению к поперечному сечению тела. Мера внутренних сил, возникающих в теле под влиянием внешних воздействий (ВШС), называется механическим напряжением (Напряжение – это сила, приходящаяся на единицу площади). - нормальное напряжение направленно по нормали (перпендикулярно) к рассматриваемому сечению - касательное напряжение направленно по касательной по отношению к рассматриваемому сечению детали При обозначении напряжений добавляют индексы, поясняющие вид деформаций: р (растяжение), с (сжатие), ср (срез при сдвиге), кр (кручение), изг (изгиб), см (смятие) y y F g Р - диагональ параллелепипеда, построенного на векторах нормального и касательных напряжений, является полным напряжением. р Единице механического напряжения присвоено наименование Паскаль (Па). х z z m

Вопрос 8 Укажите взаимосвязь между видами внутренних силовых факторов и видами напряжений. y F My N x N- продольная сила Qy-поперечная сила Qz-поперечная сила Mx-крутящий момент My-изгибающий момент Mz-изгибающий момент Qy P Qz мх Mz z у y F g р Нормальное напряжение- σ Касательные напряжения. Полное напряжение- p х z м

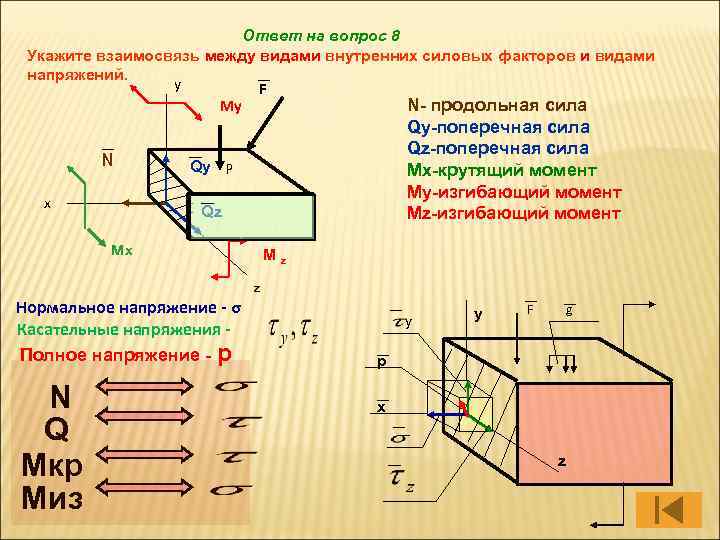
Ответ на вопрос 8 Укажите взаимосвязь между видами внутренних силовых факторов и видами напряжений. y F N- продольная сила My N x Qy-поперечная сила Qz-поперечная сила Mx-крутящий момент My-изгибающий момент Mz-изгибающий момент Qy P Qz мх Mz z Нормальное напряжение - σ Касательные напряжения Полное напряжение - p N Q Мкр Миз у y F g р х z

Вопрос 9 Укажите виды механических напряжений в зависимости от величины. Дайте их определение.

Ответ на вопрос 9 Укажите виды механических напряжений в зависимости от величины. Дайте их определение. В зависимости от величины рассматривают три вида напряжения: допускаемое, предельное, рабочее. Предельным напряжением(Пр. Н) считают напряжение, при котором происходит разрушение материала образца или возникают заметные пластические деформации. Для пластичных материалов предельным напряжением считают предел текучести для хрупких материалов - пределы прочности при растяжении и сжатии Для пластично-хрупких материалов (на диаграмме растяжения не имеющих выраженные площадки текучести) предельным напряжением считают напряжение соответствующее максимальной деформации 0, 2% ( ) Допускаемое напряжение - максимальное напряжение, обеспечивающее безопасную работу конструкции. Допускаемое напряжение- это часть предельного. где, - Допускаемое напряжение; -допускаемый коэффициент запаса прочности, зависящий от качества материала, условий работы деталей, их назначения, точности обработки, расчёта и т. д; S-фактический коэффициент прочности. Рабочее напряжение(РН)-напряжение, возникающее при работе.

Вопрос 10 В чем заключаются две формы условия прочности деталей конструкций для любой деформации?

Ответ на вопрос 10 В чем заключаются две формы условия прочности деталей конструкций для любой деформации? Первая форма условия прочности: -фактический коэффициент запаса прочности должен быть больше или равен допускаемому Вторая форма условия прочности (в общем виде для любой деформации): -рабочее напряжение должно быть меньше или равно допускаемому где, РН- рабочее напряжение, (касательное , и нормальное ); ВСФ- внутренние силовые факторы, (продольная сила N, поперечные силы Q, момент крутящий Мкр, изгибающие моменты Мизг. ГХС или ГХП- геометрические характеристики сечения или геометрические характеристики прочности: площади Ар, Аср, Асм при растяжении, сжатии, срезе, смятии; Wр - полярный момент сопротивлений при кручении; Wос, Wz- осевые моменты сопротивления при изгибе с кручением

Вопрос 11 Используя условия прочности в общем виде выполняются три вида расчётов на прочность (проверочный, проектный, определение допускаемой нагрузки). В чём заключаются эти расчёты?

Ответ 11 В чем заключаются расчеты на прочность (проверочный, проектный, определение допускаемой нагрузки)для любой деформации. 1. Проверочный расчёт - определение рабочего напряжения и сравнение его с допускаемым (известны нагрузки, материал, размеры детали; необходимо проверить обеспечена ли прочность ( перегрузка ≤ 5%, недогрузка ≤ 10%) Прочно? 2. Проектный расчёт ГХС≥ВСФ/[ДН] Определение геометрических характеристик сечений, далее -размеров сечений тела, например диаметра, номера проката и пр. (задана расчётная схема нагрузки, материал конструкции, размеры деталей подбираются, например: определяется диаметр, номер проката и т. д. ) 3. Определение допускаемой (максимальной) нагрузки [ВСФ]≤ГХС×[ДН] Определение допускаемого значения внутренних силовых факторов. (по заданному размеру сечения и допускаемому напряжению необходимо найти допускаемое значение рабочей нагрузки – [N], [Q], [Мкр], [Мизг])

Сводная таблица My Qy x N мх y Основные характеристики деформаций растяжения и сжатия y F g у N- продольная сила y F Нормальное напряжение- σ Qy-поперечная сила Qz-поперечная сила Mx-крутящий момент My-изгибающий момент Mz-изгибающий момент P Qz Mz p Касательные напряжения. Полное напряжение- p x х z z z Схема конструкций (ВШС) Внутренние силовые факторы (ВСФ) 1 F N а N≠ 0 Растяжение N=∑Fix F N F(+) N F F(-) ∑Fix - F F N N≠ 0 б Сжатие Вид напряжений Распределение напряжения по сечению; условие прочности, расчёты на прочность 3 2 F Модуль и знак ВСФ алгебраические суммы проекций внешних сил на оси координат 4 р Нормальные напряжения равномерное Эσр σ=N/A≤[σ] σ≤[σ] А≥N/[σ] [N]≤A[σ] сж

Сводная таблица My Qy x Основные характеристики деформации среза y F P N Qz мх Mz z N- продольная сила Qy-поперечная сила Qz-поперечная сила Mx-крутящий момент My-изгибающий момент Mz-изгибающий момент Схема конструкций (ВШС) 1 F у p F g Нормальное напряжение- σ Касательные напряжения. Полное напряжение- p x х z z Внутренние силовые факторы (ВСФ) 2 Модуль и знак ВСФ 3 Вид напряжений Распределение напряжения по сечению; условие прочности, расчёты на прочность 4 - касательное напряжение F F Q F y y Q ≠ 0 - сдвиг (срезсдвиг, доведённый до разрушения) (+) Q F F Qy=∑Fiy Qz=∑Fiz (-) равномерное Э

Сводная таблица My Qy x Основные характеристики деформации смятия y F P N Qz мх Mz z N- продольная сила Qy-поперечная сила Qz-поперечная сила Mx-крутящий момент My-изгибающий момент Mz-изгибающий момент Схема конструкций (ВШС) 1 у p Внутренние силовые факторы (ВСФ) 2 N N ≠ 0, (смятие- местная деформация сжатия, возникающая на наружной поверхности деталей) l. Nl = l. Fl F g Нормальное напряжение- σ Касательные напряжения. Полное напряжение- p x х F F y y z z Вид напряжений Распределение напряжения по сечению; условие прочности, расчёты на прочность 3 σсм – нормальное напряжение считают равномерно Закон распределения напряжения сложный, расчёт ведут упрощённо. За расчётную площадь смятия принимают проекцию поверхности полуцилиндра на диаметральную плоскость

F- площадь сечения, Р- внешняя нагрузка

Р- окружное усилие

Р- внешняя нагрузка

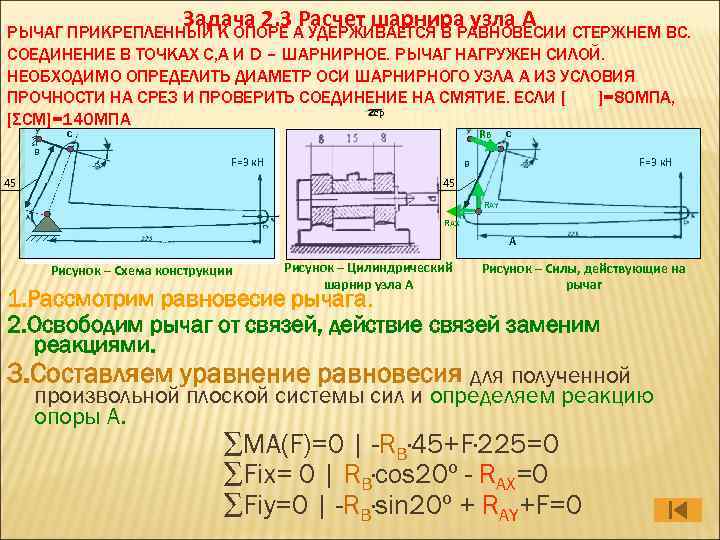
Задача 2. 3 Расчет шарнира узла А РЫЧАГ ПРИКРЕПЛЕННЫЙ К ОПОРЕ А УДЕРЖИВАЕТСЯ В РАВНОВЕСИИ СТЕРЖНЕМ ВС. СОЕДИНЕНИЕ В ТОЧКАХ C, A И D – ШАРНИРНОЕ. РЫЧАГ НАГРУЖЕН СИЛОЙ. НЕОБХОДИМО ОПРЕДЕЛИТЬ ДИАМЕТР ОСИ ШАРНИРНОГО УЗЛА А ИЗ УСЛОВИЯ ПРОЧНОСТИ НА СРЕЗ И ПРОВЕРИТЬ СОЕДИНЕНИЕ НА СМЯТИЕ. ЕСЛИ [ ]=80 МПА, ср [ΣСМ]=140 МПА с в RB F=3 к. Н 45 с F=3 к. Н в 45 RАY RАX А Рисунок – Схема конструкции Рисунок – Цилиндрический шарнир узла А Рисунок – Силы, действующие на рычаг 1. Рассмотрим равновесие рычага. 2. Освободим рычаг от связей, действие связей заменим реакциями. 3. Составляем уравнение равновесия для полученной произвольной плоской системы сил и определяем реакцию опоры А. ∑МА(F)=0 | -RB· 45+F· 225=0 ∑Fix= 0 | RB·cos 20º - RAX=0 ∑Fiy=0 | -RB·sin 20º + RAY+F=0

Имеем систему 3 -х уравнений с неизвестными, то есть задача статически определимая. Из первого уравнения выражаем RB RB=F· 225 / 45=3· 225 / 45=15 к. Н Из второго уравнения выражаем RAX= RB·cos 20º=15· 0. 94=14. 1 к. Н Из третьего уравнения выражаем RAY= -F+RB·sin 20º=-3+15· 0. 342=2. 1 к. Н 4. Полная реакция опоры А RA=√RAX 2 + RAY 2 =√ 14. 12 + 2. 12 =14. 14 к. Н

5. Поперечная сила для оси шарнира численно равна реакции опоры А. |Q|=|RA|=14. 14 к. Н 6. Используя условие прочности на срез, определим диаметр оси шарнира. =Q / n·Aср. ≤ [ ] Аср= Q/n[ ] А= πd 2/4 ср ср ср n – количество плоскостей среза; n=2 d≥√ 4 Q/nπ[ ] d≥√ 4*14. 14*103 /2*3. 14*80 d≥ 10. 61 мм принимаем d=12 мм ср

7. Определяем фактическое напряжение смятия и сравниваем его с допускаемым. σсм=Q / n·Aср. σсм= 14. 26· 103 / 12· 15=79 МПа σсм=79 МПа < [σсм]=140 МПа Фактическое напряжение смятия получается меньше допустимого, значит условие прочности соблюдается и соединение работает с недогрузкой. Ответ: диаметр оси шарнирного узла А принимаем 12 мм.

ВЫВОДЫ УРОКА Повторили и обобщили понятий характерных для всех деформаций Вывели основных положений характерных для деформаций срез и смятие. Решили задачу на срез и смятие.