61d4234862cfe5b275b23a1dff000e1a.ppt
- Количество слайдов: 19
 SERIES RL CIRCUITS (1) • • • Circuit above is a series RL network connected to an ac voltage source Need to find the phasor form of the total impedance of this combination The total impedance of this series combination is The magnitude and angle of ZT can be found by converting to polar form: |ZT| = √[R 2+(ωL)2] and θ = tan-1(ωL/R) The plot of ZT: Im jωL |Z T| θ R Series and Parallel AC Circuits Re 1
SERIES RL CIRCUITS (1) • • • Circuit above is a series RL network connected to an ac voltage source Need to find the phasor form of the total impedance of this combination The total impedance of this series combination is The magnitude and angle of ZT can be found by converting to polar form: |ZT| = √[R 2+(ωL)2] and θ = tan-1(ωL/R) The plot of ZT: Im jωL |Z T| θ R Series and Parallel AC Circuits Re 1
 SERIES RL CIRCUITS (2) • Example: For a series RL combination circuit, R = 300 , L = 0. 2 H and e(t) = 17 sin(2000 t) V. Find the total equivalent impedance in polar form and rectangular form. Sketch the impedance in the complex plane. • We can use Ohm’s law to find the total current supplied by a voltage source: i. T = v / ZT Mathematical operation must be carried out using phasors since all quantities have both magnitude and angle The current i. T in a series circuit is the same through every series-connected component The ac voltage drop across each component can be found by multiplying each impedance by the current v 1 = i. TZ 1, v 2 = i. TZ 2, … • • • Example: In a series RL circuit, where e(t) = 30 0 V, R = 200 , XL = j 100. Find the total current in the circuit. Find the voltage drops across R and L. Verify KVL around the circuit. Draw a phasor diagram showing e, v. R, v. L and i. T. Sketch the voltage waveforms. Series and Parallel AC Circuits 2
SERIES RL CIRCUITS (2) • Example: For a series RL combination circuit, R = 300 , L = 0. 2 H and e(t) = 17 sin(2000 t) V. Find the total equivalent impedance in polar form and rectangular form. Sketch the impedance in the complex plane. • We can use Ohm’s law to find the total current supplied by a voltage source: i. T = v / ZT Mathematical operation must be carried out using phasors since all quantities have both magnitude and angle The current i. T in a series circuit is the same through every series-connected component The ac voltage drop across each component can be found by multiplying each impedance by the current v 1 = i. TZ 1, v 2 = i. TZ 2, … • • • Example: In a series RL circuit, where e(t) = 30 0 V, R = 200 , XL = j 100. Find the total current in the circuit. Find the voltage drops across R and L. Verify KVL around the circuit. Draw a phasor diagram showing e, v. R, v. L and i. T. Sketch the voltage waveforms. Series and Parallel AC Circuits 2
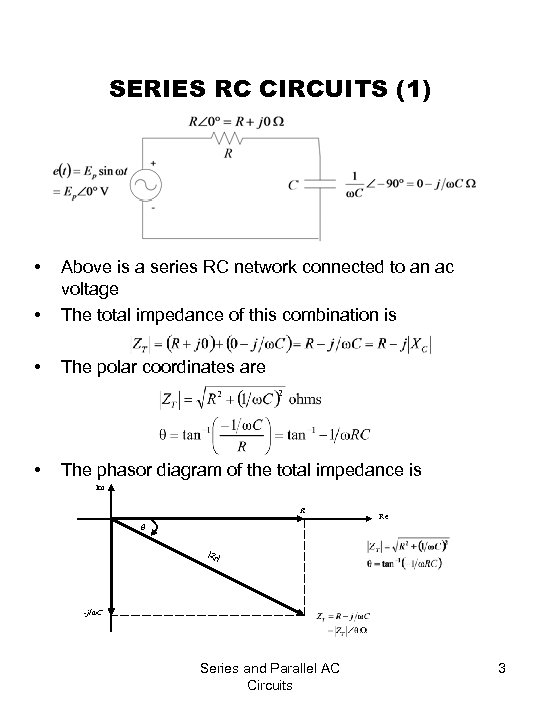 SERIES RC CIRCUITS (1) • • Above is a series RC network connected to an ac voltage The total impedance of this combination is • The polar coordinates are • The phasor diagram of the total impedance is Im R Re θ |Z | T -j/ωC Series and Parallel AC Circuits 3
SERIES RC CIRCUITS (1) • • Above is a series RC network connected to an ac voltage The total impedance of this combination is • The polar coordinates are • The phasor diagram of the total impedance is Im R Re θ |Z | T -j/ωC Series and Parallel AC Circuits 3
 SERIES RC CIRCUITS (2) • • • As in the series RL circuit, the total current supplied to the RC network and the voltage drops can be found by using Ohm’s Law: i. T = e / Z T v. R = i. TR and v. C = i. TXC Example: For a series RC circuit where e(t) = 18 sin(240 t + 45 ) V, R = 3. 3 k and C = 2. 2µF: a) Find the total current in the circuit in phasor and sinusoidal form b) Find the voltage drops across the resistor and capacitor in phasor and sinusoidal form c) Verify KVL around the circuit d) Draw a phasor diagram showing e, i. T, v. R and v. C e) Sketch the waveforms of e, v. R and v. C versus angle Series and Parallel AC Circuits 4
SERIES RC CIRCUITS (2) • • • As in the series RL circuit, the total current supplied to the RC network and the voltage drops can be found by using Ohm’s Law: i. T = e / Z T v. R = i. TR and v. C = i. TXC Example: For a series RC circuit where e(t) = 18 sin(240 t + 45 ) V, R = 3. 3 k and C = 2. 2µF: a) Find the total current in the circuit in phasor and sinusoidal form b) Find the voltage drops across the resistor and capacitor in phasor and sinusoidal form c) Verify KVL around the circuit d) Draw a phasor diagram showing e, i. T, v. R and v. C e) Sketch the waveforms of e, v. R and v. C versus angle Series and Parallel AC Circuits 4
 SERIES RLC CIRCUITS (1) • The total impedance of the RLC circuit is • • • In terms of magnitudes it is: ZT = R + j(|XL| - |XC|) Inductive and capacitive reactance have opposite signs Thus net reactance may be either inductive or capacitive, depending which is larger Polar coordinates are • Series and Parallel AC Circuits 5
SERIES RLC CIRCUITS (1) • The total impedance of the RLC circuit is • • • In terms of magnitudes it is: ZT = R + j(|XL| - |XC|) Inductive and capacitive reactance have opposite signs Thus net reactance may be either inductive or capacitive, depending which is larger Polar coordinates are • Series and Parallel AC Circuits 5
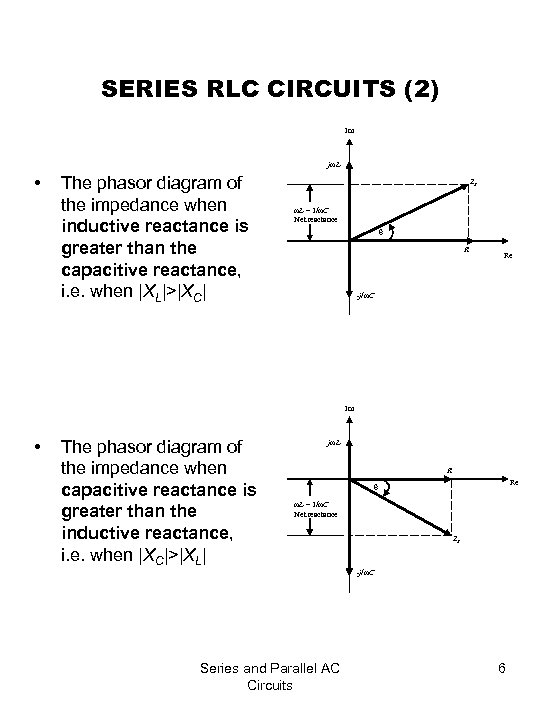 SERIES RLC CIRCUITS (2) Im jωL • The phasor diagram of the impedance when inductive reactance is greater than the capacitive reactance, i. e. when |XL|>|XC| ZT ωL – 1/ωC Net reactance θ R Re -j/ωC Im • The phasor diagram of the impedance when capacitive reactance is greater than the inductive reactance, i. e. when |XC|>|XL| jωL R Re θ ωL – 1/ωC Net reactance ZT -j/ωC Series and Parallel AC Circuits 6
SERIES RLC CIRCUITS (2) Im jωL • The phasor diagram of the impedance when inductive reactance is greater than the capacitive reactance, i. e. when |XL|>|XC| ZT ωL – 1/ωC Net reactance θ R Re -j/ωC Im • The phasor diagram of the impedance when capacitive reactance is greater than the inductive reactance, i. e. when |XC|>|XL| jωL R Re θ ωL – 1/ωC Net reactance ZT -j/ωC Series and Parallel AC Circuits 6
 SERIES RLC CIRCUITS (3) • When there is more than one resistor, capacitor and/or inductor in a series circuit, the total impedance has a resistance component equal to the sum of the resistance values and a reactive component equal to the sum of the capacitive reactances subtracted from the sum of the inductive reactances • Example: In a series RLC circuit, e(t) = 100 sinωt, R = 800 , ZL = j 1250 and ZC = -j 450. a) Find the current in polar form b) Find the voltage drops v. R, v. L, v. C c) Verify KVL around the circuit d) Draw a phasor diagram showing e, i, v. R, v. L, v. C • • Series and Parallel AC Circuits 7
SERIES RLC CIRCUITS (3) • When there is more than one resistor, capacitor and/or inductor in a series circuit, the total impedance has a resistance component equal to the sum of the resistance values and a reactive component equal to the sum of the capacitive reactances subtracted from the sum of the inductive reactances • Example: In a series RLC circuit, e(t) = 100 sinωt, R = 800 , ZL = j 1250 and ZC = -j 450. a) Find the current in polar form b) Find the voltage drops v. R, v. L, v. C c) Verify KVL around the circuit d) Draw a phasor diagram showing e, i, v. R, v. L, v. C • • Series and Parallel AC Circuits 7
 ADMITTANCE • • The reciprocal of resistance is conductance, with units Siemens The reciprocal of impedance is admittance, denoted Y Y = 1/Z siemens Impedance is a measure of the extent to which a component impedes the flow of ac current through it Admittance is a measure of how well it admits the flow of ac current The greater the admittance, the smaller the impedance, and vice versa Resistance R is one form of impedance Z, conductance G is one form of admittance Y Phasor form of conductance is: Series and Parallel AC Circuits 8
ADMITTANCE • • The reciprocal of resistance is conductance, with units Siemens The reciprocal of impedance is admittance, denoted Y Y = 1/Z siemens Impedance is a measure of the extent to which a component impedes the flow of ac current through it Admittance is a measure of how well it admits the flow of ac current The greater the admittance, the smaller the impedance, and vice versa Resistance R is one form of impedance Z, conductance G is one form of admittance Y Phasor form of conductance is: Series and Parallel AC Circuits 8
 SUSCEPTANCE • • • Reactance is another special case of impedance The reciprocal of reactance is called susceptance, B B = 1/X siemens There are two types of susceptance Inductive susceptance: • Capacitive susceptance: • • Z = 1/Y; R = 1/G; XL = 1/BL; XC = 1/BC Example: Find the admittance of a 5 resistor; a 5 m. H inductor at f = 60 Hz; a 0. 2µF capacitor at ω = 1. 25 106 rad/s. Example: Find the admittance Y corresponding to Z = 30 + j 40 . Draw a phasor diagram showing Y in the complex plane. • Series and Parallel AC Circuits 9
SUSCEPTANCE • • • Reactance is another special case of impedance The reciprocal of reactance is called susceptance, B B = 1/X siemens There are two types of susceptance Inductive susceptance: • Capacitive susceptance: • • Z = 1/Y; R = 1/G; XL = 1/BL; XC = 1/BC Example: Find the admittance of a 5 resistor; a 5 m. H inductor at f = 60 Hz; a 0. 2µF capacitor at ω = 1. 25 106 rad/s. Example: Find the admittance Y corresponding to Z = 30 + j 40 . Draw a phasor diagram showing Y in the complex plane. • Series and Parallel AC Circuits 9
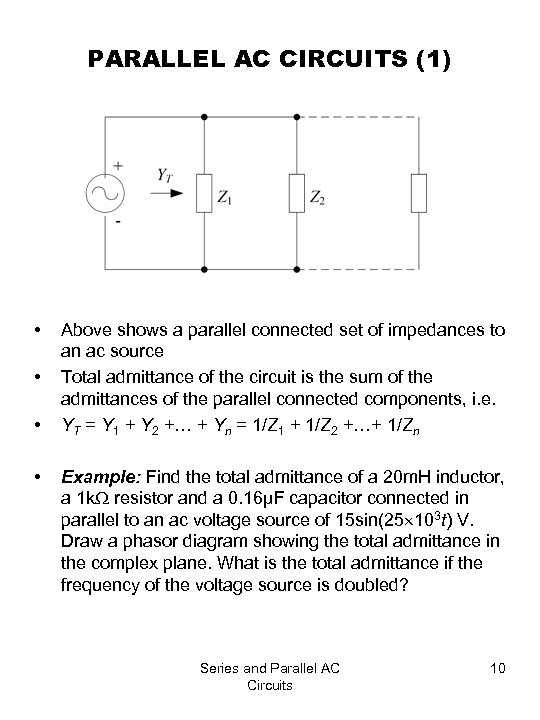 PARALLEL AC CIRCUITS (1) • • Above shows a parallel connected set of impedances to an ac source Total admittance of the circuit is the sum of the admittances of the parallel connected components, i. e. YT = Y 1 + Y 2 +… + Yn = 1/Z 1 + 1/Z 2 +…+ 1/Zn Example: Find the total admittance of a 20 m. H inductor, a 1 k resistor and a 0. 16µF capacitor connected in parallel to an ac voltage source of 15 sin(25 103 t) V. Draw a phasor diagram showing the total admittance in the complex plane. What is the total admittance if the frequency of the voltage source is doubled? Series and Parallel AC Circuits 10
PARALLEL AC CIRCUITS (1) • • Above shows a parallel connected set of impedances to an ac source Total admittance of the circuit is the sum of the admittances of the parallel connected components, i. e. YT = Y 1 + Y 2 +… + Yn = 1/Z 1 + 1/Z 2 +…+ 1/Zn Example: Find the total admittance of a 20 m. H inductor, a 1 k resistor and a 0. 16µF capacitor connected in parallel to an ac voltage source of 15 sin(25 103 t) V. Draw a phasor diagram showing the total admittance in the complex plane. What is the total admittance if the frequency of the voltage source is doubled? Series and Parallel AC Circuits 10
 PARALLEL AC CIRCUITS (2) • • The total impedance of a network is the reciprocal of its total admittance, ZT = 1/YT For a parallel network: • Example: Three components (an inductor with impedance j 10 , a resistor with impedance 2 , and another inductor with impedance j 5 ) are connected in parallel. Find the total equivalent impedance of this network. • Example: A capacitor with impedance –j 100 and an inductor with impedance j 500 are connected in parallel. Find this network’s total equivalent impedance. Series and Parallel AC Circuits 11
PARALLEL AC CIRCUITS (2) • • The total impedance of a network is the reciprocal of its total admittance, ZT = 1/YT For a parallel network: • Example: Three components (an inductor with impedance j 10 , a resistor with impedance 2 , and another inductor with impedance j 5 ) are connected in parallel. Find the total equivalent impedance of this network. • Example: A capacitor with impedance –j 100 and an inductor with impedance j 500 are connected in parallel. Find this network’s total equivalent impedance. Series and Parallel AC Circuits 11
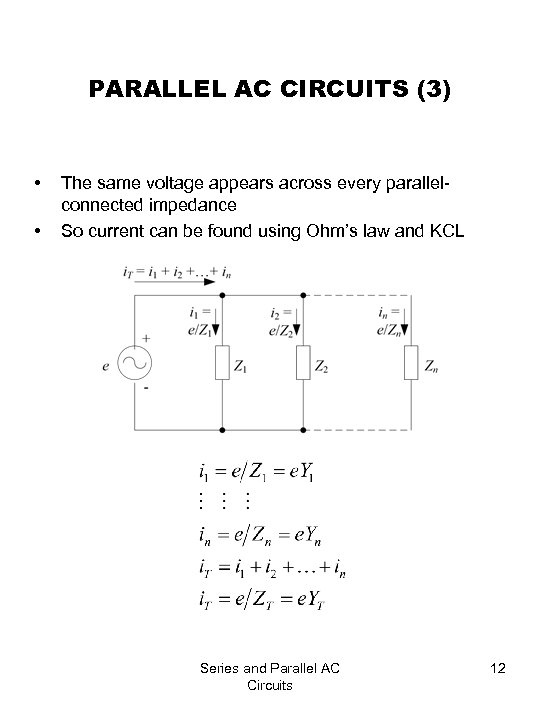 PARALLEL AC CIRCUITS (3) • • The same voltage appears across every parallelconnected impedance So current can be found using Ohm’s law and KCL Series and Parallel AC Circuits 12
PARALLEL AC CIRCUITS (3) • • The same voltage appears across every parallelconnected impedance So current can be found using Ohm’s law and KCL Series and Parallel AC Circuits 12
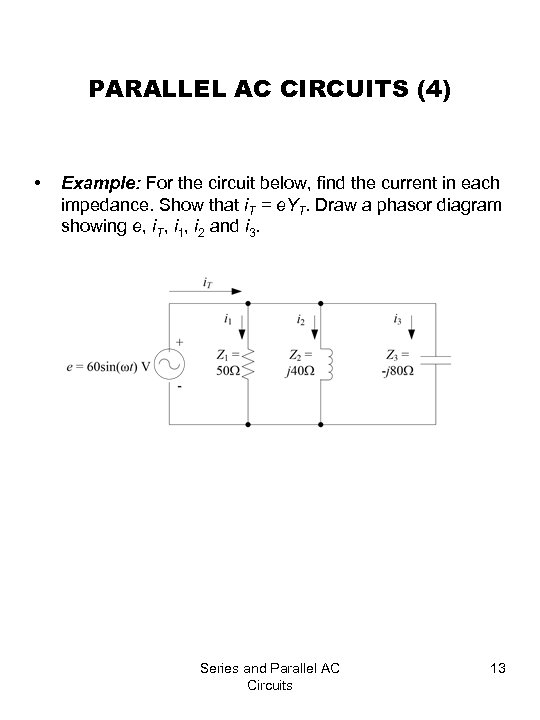 PARALLEL AC CIRCUITS (4) • Example: For the circuit below, find the current in each impedance. Show that i. T = e. YT. Draw a phasor diagram showing e, i. T, i 1, i 2 and i 3. Series and Parallel AC Circuits 13
PARALLEL AC CIRCUITS (4) • Example: For the circuit below, find the current in each impedance. Show that i. T = e. YT. Draw a phasor diagram showing e, i. T, i 1, i 2 and i 3. Series and Parallel AC Circuits 13
 AC CURRENT SOURCES (1) • • • Like a dc current source, an ideal ac current source supplies the same constant current to whatever network is connected across its terminals For ac, the current is constant in the sense that its peak value does not change The same symbol is used for an ac current source as for a dc current source The direction of the arrow is just a phase reference, since current reverses direction every half cycle Reversing the arrow is the same as multiplying the current by -1, which is the same as adding or subtracting 180 from its phase angle Series and Parallel AC Circuits 14
AC CURRENT SOURCES (1) • • • Like a dc current source, an ideal ac current source supplies the same constant current to whatever network is connected across its terminals For ac, the current is constant in the sense that its peak value does not change The same symbol is used for an ac current source as for a dc current source The direction of the arrow is just a phase reference, since current reverses direction every half cycle Reversing the arrow is the same as multiplying the current by -1, which is the same as adding or subtracting 180 from its phase angle Series and Parallel AC Circuits 14
 AC CURRENT SOURCES (2) • Example: For the circuit below, find the voltage v. T across the ac current source. Find the currents i 1 and i 2. Show that i = i 1 + i 2. Draw a phasor diagram showing i, v. T, i 1 and i 2. Sketch the waveforms of i, i 1 and i 2 versus angle. Series and Parallel AC Circuits 15
AC CURRENT SOURCES (2) • Example: For the circuit below, find the voltage v. T across the ac current source. Find the currents i 1 and i 2. Show that i = i 1 + i 2. Draw a phasor diagram showing i, v. T, i 1 and i 2. Sketch the waveforms of i, i 1 and i 2 versus angle. Series and Parallel AC Circuits 15
 POWER IN CIRCUITS CONTAINING REACTANCE (1) • Recall that the average power dissipated by a resistance carrying sinusoidal ac current can be found by • Above can be used to find Pavg dissipated by a resistor in a circuit containing reactance, provided the values used in the computations are indeed those of the voltage across and/or current through the resistor itself In many practical circuits, it is sometimes necessary to compute Pavg when the resistance or resistor voltage/current are not known • Series and Parallel AC Circuits 16
POWER IN CIRCUITS CONTAINING REACTANCE (1) • Recall that the average power dissipated by a resistance carrying sinusoidal ac current can be found by • Above can be used to find Pavg dissipated by a resistor in a circuit containing reactance, provided the values used in the computations are indeed those of the voltage across and/or current through the resistor itself In many practical circuits, it is sometimes necessary to compute Pavg when the resistance or resistor voltage/current are not known • Series and Parallel AC Circuits 16
 POWER IN CIRCUITS CONTAINING REACTANCE (2) • • Above is an ac circuit with a general impedance Z Assuming that the voltage supplied has angle • • Angle between voltage and current is - ( - ) = The angle between the voltage applied to a network and the total current supplied to it equals the angle of the impedance of the network Resistive component of impedance Z is R = |Z|cos ohms Since only resistance in network dissipates power • • Series and Parallel AC Circuits 17
POWER IN CIRCUITS CONTAINING REACTANCE (2) • • Above is an ac circuit with a general impedance Z Assuming that the voltage supplied has angle • • Angle between voltage and current is - ( - ) = The angle between the voltage applied to a network and the total current supplied to it equals the angle of the impedance of the network Resistive component of impedance Z is R = |Z|cos ohms Since only resistance in network dissipates power • • Series and Parallel AC Circuits 17
 POWER FACTOR • • • Equations on previous slide provide a means for computing the average power in terms of voltage e across whole network and total supply current i Cos is called the power factor For a purely resistive network, voltage and current are in phase, so power factor = cos 0 = 1 → Pavg = Ep. Ip / 2 For a purely reactive network, voltage and current are separated by ± 90 , and cos ± 90 = 0 → Pavg = 0, i. e no power is dissipated by purely reactive components (capacitors and inductors) Since Vp = 2 Veff and Ip = 2 Ieff we can derive Series and Parallel AC Circuits 18
POWER FACTOR • • • Equations on previous slide provide a means for computing the average power in terms of voltage e across whole network and total supply current i Cos is called the power factor For a purely resistive network, voltage and current are in phase, so power factor = cos 0 = 1 → Pavg = Ep. Ip / 2 For a purely reactive network, voltage and current are separated by ± 90 , and cos ± 90 = 0 → Pavg = 0, i. e no power is dissipated by purely reactive components (capacitors and inductors) Since Vp = 2 Veff and Ip = 2 Ieff we can derive Series and Parallel AC Circuits 18
 EXAMPLE OF POWER IN AC CIRCUITS • • In the circuit above: Find the power factor Use the power factor to find the average power dissipated in the network Verify that the power computed above is the same as the power computed by using the voltage across and current through the resistor Series and Parallel AC Circuits 19
EXAMPLE OF POWER IN AC CIRCUITS • • In the circuit above: Find the power factor Use the power factor to find the average power dissipated in the network Verify that the power computed above is the same as the power computed by using the voltage across and current through the resistor Series and Parallel AC Circuits 19


