sequential_FSM.ppt
- Количество слайдов: 33
 Sequential System Synthesis -- Finite State Machine
Sequential System Synthesis -- Finite State Machine
 Outline: Finite State Machine > Definitions > FSM Representations = = = State Transition Graph (STG) Flow Table Cube Table > State Minimization = Completely Specified FSM = Incompletely Specified Machine (ISM) > State Encoding ENEE 644 2
Outline: Finite State Machine > Definitions > FSM Representations = = = State Transition Graph (STG) Flow Table Cube Table > State Minimization = Completely Specified FSM = Incompletely Specified Machine (ISM) > State Encoding ENEE 644 2
 Definition: Finite State Machine > A Finite State Machine (FSM) of Mealy type is a 6 tuple
Definition: Finite State Machine > A Finite State Machine (FSM) of Mealy type is a 6 tuple
 Example: Finite State Machine > I = {x, y} > S = {A, B, C} > S 0= {A} > (A, x) = A, (B, x) = A, (C, x) = C (A, y) = B, (B, y) = C, (C, y) = A > O = {0, 1} > (A, x) = 0, (B, x) = 0, (C, x) = 0 (A, y) = 1, (B, y) = 0, (C, y) = 1 ENEE 644 4
Example: Finite State Machine > I = {x, y} > S = {A, B, C} > S 0= {A} > (A, x) = A, (B, x) = A, (C, x) = C (A, y) = B, (B, y) = C, (C, y) = A > O = {0, 1} > (A, x) = 0, (B, x) = 0, (C, x) = 0 (A, y) = 1, (B, y) = 0, (C, y) = 1 ENEE 644 4
 FSM Representation: STG > State Transition Graph: = Node state (S) = Edge transition ( : Sx. I S, : Sx. I O, S 0) • Direction: from the current state to the next state • Label: input/output information for the transition • Special edges: edges without source, their ending nodes are initial states In sum, a STG is a weighted, directed graph where self loops and duplicated edges are allowed. Each node has at most |I| outgoing edges and |I|x|S| incoming edges. Total number of edges is |I|x|S|+|S 0|. ENEE 644 5
FSM Representation: STG > State Transition Graph: = Node state (S) = Edge transition ( : Sx. I S, : Sx. I O, S 0) • Direction: from the current state to the next state • Label: input/output information for the transition • Special edges: edges without source, their ending nodes are initial states In sum, a STG is a weighted, directed graph where self loops and duplicated edges are allowed. Each node has at most |I| outgoing edges and |I|x|S| incoming edges. Total number of edges is |I|x|S|+|S 0|. ENEE 644 5
 Example: FSM as an STG > > > I = {x, y} S = {A, B, C} S 0= {A} x/0 A > (A, x) = A, (A, y) = B, (B, x) = A, (B, y) = C, (C, x) = C, (C, y) = A > O = {0, 1} > (A, x) = 0, (A, y) = 1, (B, x) = 0, (B, y) = 0, (C, x) = 0, (C, y) = 1 ENEE 644 y/1 x/0 B y/0 y/1 C x/0 6
Example: FSM as an STG > > > I = {x, y} S = {A, B, C} S 0= {A} x/0 A > (A, x) = A, (A, y) = B, (B, x) = A, (B, y) = C, (C, x) = C, (C, y) = A > O = {0, 1} > (A, x) = 0, (A, y) = 1, (B, x) = 0, (B, y) = 0, (C, x) = 0, (C, y) = 1 ENEE 644 y/1 x/0 B y/0 y/1 C x/0 6
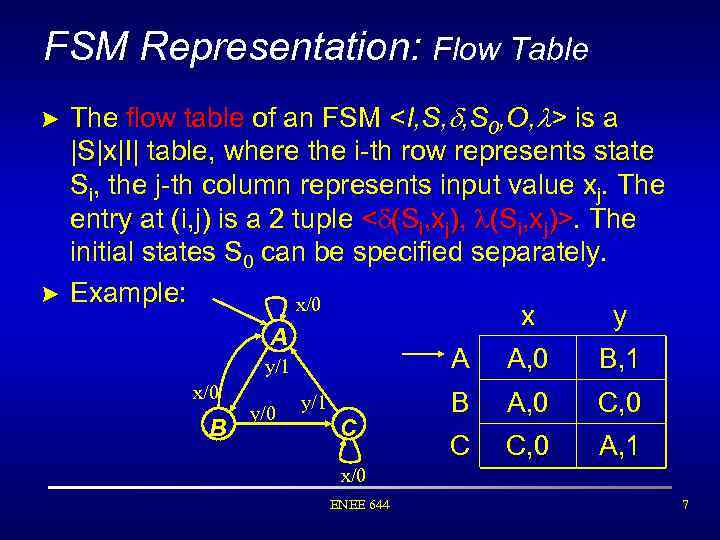 FSM Representation: Flow Table > The flow table of an FSM
FSM Representation: Flow Table > The flow table of an FSM
 FSM Representation: Cube Table > The cube table of an FSM
FSM Representation: Cube Table > The cube table of an FSM
 FSM with Incomplete Specification > An FSM
FSM with Incomplete Specification > An FSM
 Make Incomplete Complete > In STG: add a dummy state called trap state. > In flow table: leave the entry empty or fill it by
Make Incomplete Complete > In STG: add a dummy state called trap state. > In flow table: leave the entry empty or fill it by
 FSM Minimization > FSMs may contain redundant states, i. e. states whose function can be accomplished by other states. > Removing the redundant states decreases the number of states in the FSM, and in general results in a simplification in the final implementation. > State minimization is the transformation of a given FSM into an equivalent FSM with no redundant states (I. e. minimal number of states). ENEE 644 11
FSM Minimization > FSMs may contain redundant states, i. e. states whose function can be accomplished by other states. > Removing the redundant states decreases the number of states in the FSM, and in general results in a simplification in the final implementation. > State minimization is the transformation of a given FSM into an equivalent FSM with no redundant states (I. e. minimal number of states). ENEE 644 11
 Binary Relations > Given two sets A and B, a binary relation R between A and B is a subset of Ax. B={(x, y)|x A, y B}. We write x. R y if (x, y) R. > Relation R Bx. B is = = reflexive iff x. Rx for any x B; compatibility relation symmetric iff x. R y y. R x; anti-symmetric iff x. R y, y. R x x=y; transitive iff x. R y, y. R z x. R z. > A binary relation R Bx. B is an equivalent relation if it is reflexive, symmetric, and transitive. ENEE 644 12
Binary Relations > Given two sets A and B, a binary relation R between A and B is a subset of Ax. B={(x, y)|x A, y B}. We write x. R y if (x, y) R. > Relation R Bx. B is = = reflexive iff x. Rx for any x B; compatibility relation symmetric iff x. R y y. R x; anti-symmetric iff x. R y, y. R x x=y; transitive iff x. R y, y. R z x. R z. > A binary relation R Bx. B is an equivalent relation if it is reflexive, symmetric, and transitive. ENEE 644 12
 Partition into Equivalent Classes > A partition of a set of B is a set of subsets Bi B, such that = Bi Bi ( i j) = i B i = B. > Given an equivalent relation R Bx. B, the equivalent class of x B is [x]={y B|x. Ry}. = x, y B, [x]=[y] or [x] [y]= ; = If B 1, B 2, …, Bn are all the different equivalent classes, then {B 1, B 2, …, Bn} is a partition of B. An equivalent relation gives a unique partition. ENEE 644 13
Partition into Equivalent Classes > A partition of a set of B is a set of subsets Bi B, such that = Bi Bi ( i j) = i B i = B. > Given an equivalent relation R Bx. B, the equivalent class of x B is [x]={y B|x. Ry}. = x, y B, [x]=[y] or [x] [y]= ; = If B 1, B 2, …, Bn are all the different equivalent classes, then {B 1, B 2, …, Bn} is a partition of B. An equivalent relation gives a unique partition. ENEE 644 13
 Refinement of a Partition > Given two partitions P 1={B 11, B 21, …, Bm 1} and P 2={B 12, B 22, …, Bn 2} of a set B, P 1 is a refinement of P 2 if every subset (block) Bi 1 Bj 2 for some j. > Let P 1={B 11, B 21, …, Bm 1} and P 2={B 12, B 22, …, Bn 2} be two sets of subsets of a set B, the meet of P 1 and P 2 is defined as the following set: P 1 • P 2={Bi 1 Bj 2|i=1, 2, …m, j=1, 2, …, n} > Theorem: If P 1 and P 2 are partitions, then P 1 • P 2 is also a partition of the same set B, furthermore, it is a refinement for both P 1 and P 2. [Proof: ] ENEE 644 14
Refinement of a Partition > Given two partitions P 1={B 11, B 21, …, Bm 1} and P 2={B 12, B 22, …, Bn 2} of a set B, P 1 is a refinement of P 2 if every subset (block) Bi 1 Bj 2 for some j. > Let P 1={B 11, B 21, …, Bm 1} and P 2={B 12, B 22, …, Bn 2} be two sets of subsets of a set B, the meet of P 1 and P 2 is defined as the following set: P 1 • P 2={Bi 1 Bj 2|i=1, 2, …m, j=1, 2, …, n} > Theorem: If P 1 and P 2 are partitions, then P 1 • P 2 is also a partition of the same set B, furthermore, it is a refinement for both P 1 and P 2. [Proof: ] ENEE 644 14
 Equivalent States of an FSM > Given two states s and t in an FSM, and a k-string x=(x 0 x 1…xk-1), suppose zs=(zs 0 zs 1…zsk-1) and zt=(zt 0 zt 1…ztk-1) are the corresponding output strings when states s and t are used as starting state respectively. x is called a length-k distinguishing sequence for states s and t iff zsk-1 ztk-1. xk-1…x 1 x 0 s zsk-1…zs 1 zs 0 xk-1…x 1 x 0 == ? t s ztk-1…zt 1 zt 0 t ENEE 644 15
Equivalent States of an FSM > Given two states s and t in an FSM, and a k-string x=(x 0 x 1…xk-1), suppose zs=(zs 0 zs 1…zsk-1) and zt=(zt 0 zt 1…ztk-1) are the corresponding output strings when states s and t are used as starting state respectively. x is called a length-k distinguishing sequence for states s and t iff zsk-1 ztk-1. xk-1…x 1 x 0 s zsk-1…zs 1 zs 0 xk-1…x 1 x 0 == ? t s ztk-1…zt 1 zt 0 t ENEE 644 15
 Equivalent States of an FSM > Two states s and t are k-equivalent, written as > > > s kt, iff there does not exist a distinguishing sequence for s and t of length k or less. Two states are equivalent iff they are |S|equivalent. Define k={(s, t)| s kt}, the set of all pairs of kequivalent states. k is an equivalent relation, I. e. , it is = = = Reflexive: Symmetric: Transitive: s ks s kt t ks r ks, s kt r kt ENEE 644 16
Equivalent States of an FSM > Two states s and t are k-equivalent, written as > > > s kt, iff there does not exist a distinguishing sequence for s and t of length k or less. Two states are equivalent iff they are |S|equivalent. Define k={(s, t)| s kt}, the set of all pairs of kequivalent states. k is an equivalent relation, I. e. , it is = = = Reflexive: Symmetric: Transitive: s ks s kt t ks r ks, s kt r kt ENEE 644 16
 Equivalent States of an FSM > 1={(A, C), (A, E), (C, E), (B, D), (B, F), (D, F), (C, A), (E, C), (D, B), (F, D), (A, A), …, (F, F)} = B 11={A, C, E} = B 21={B, D, F} > 2={(A, C), (A, E), (C, E), (B, D), (C, A), (E, C), (D, B), (A, A), …, (F, F)} = = = 0/0 D 1/0 1/1 A F 0/0 B 12={A, C, E} B 22={B, D} B 32={F} 0/0 B 1/0 1/1 E 1/1 0/0 C > 3={(A, C), (B, D), (C, A), (D, B), (A, A), …, (F, F)} ENEE 644 17
Equivalent States of an FSM > 1={(A, C), (A, E), (C, E), (B, D), (B, F), (D, F), (C, A), (E, C), (D, B), (F, D), (A, A), …, (F, F)} = B 11={A, C, E} = B 21={B, D, F} > 2={(A, C), (A, E), (C, E), (B, D), (C, A), (E, C), (D, B), (A, A), …, (F, F)} = = = 0/0 D 1/0 1/1 A F 0/0 B 12={A, C, E} B 22={B, D} B 32={F} 0/0 B 1/0 1/1 E 1/1 0/0 C > 3={(A, C), (B, D), (C, A), (D, B), (A, A), …, (F, F)} ENEE 644 17
 Equivalent States Checking: Theory > Two states are equivalent iff they are |S|- equivalent. > Theorem 1. Let sx and tx be the x-successors of s and t in an FSM, then s k+1 t s kt and x I, sx ktx. > Theorem 2. Two states of a given FSM are equivalent iff they are (|S|)-equivalent. ENEE 644 18
Equivalent States Checking: Theory > Two states are equivalent iff they are |S|- equivalent. > Theorem 1. Let sx and tx be the x-successors of s and t in an FSM, then s k+1 t s kt and x I, sx ktx. > Theorem 2. Two states of a given FSM are equivalent iff they are (|S|)-equivalent. ENEE 644 18
 State Equivalence Checking: Practice > Goal: determine |S|(S), all pairs of equivalent states in an FSM S. > Partition-Refinement procedure: = Pk={B 1 k, B 2 k, …}: the partition determined by k, the kequivalent state pairs. (P 0=S={B 10}) = Idea: For each block in Pk • partition it (for all x I) if its x-successors are not in the same block; • Refine the partition by taking the meet of these finer partitions; Stop when Pk+1=Pk ENEE 644 19
State Equivalence Checking: Practice > Goal: determine |S|(S), all pairs of equivalent states in an FSM S. > Partition-Refinement procedure: = Pk={B 1 k, B 2 k, …}: the partition determined by k, the kequivalent state pairs. (P 0=S={B 10}) = Idea: For each block in Pk • partition it (for all x I) if its x-successors are not in the same block; • Refine the partition by taking the meet of these finer partitions; Stop when Pk+1=Pk ENEE 644 19
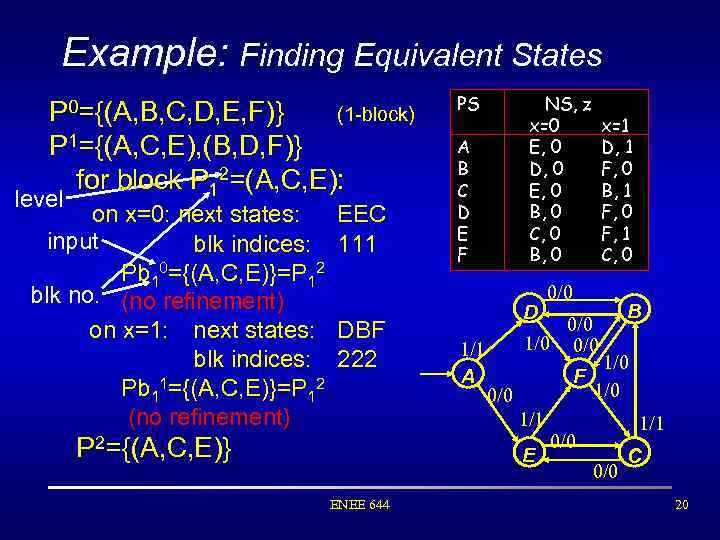 Example: Finding Equivalent States P 0={(A, B, C, D, E, F)} (1 -block) P 1={(A, C, E), (B, D, F)} for block P 12=(A, C, E): level on x=0: next states: input blk indices: Pb 10={(A, C, E)}=P 12 blk no. (no refinement) on x=1: next states: blk indices: Pb 11={(A, C, E)}=P 12 (no refinement) EEC 111 DBF 222 PS NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 A B C D E F D 1/1 A F 0/0 E ENEE 644 0/0 1/0 0/0 1/1 P 2={(A, C, E)} x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 B 1/0 1/1 0/0 C 20
Example: Finding Equivalent States P 0={(A, B, C, D, E, F)} (1 -block) P 1={(A, C, E), (B, D, F)} for block P 12=(A, C, E): level on x=0: next states: input blk indices: Pb 10={(A, C, E)}=P 12 blk no. (no refinement) on x=1: next states: blk indices: Pb 11={(A, C, E)}=P 12 (no refinement) EEC 111 DBF 222 PS NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 A B C D E F D 1/1 A F 0/0 E ENEE 644 0/0 1/0 0/0 1/1 P 2={(A, C, E)} x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 B 1/0 1/1 0/0 C 20
 Example: Finding Equivalent States PS P 1={(A, C, E), (B, D, F)} P 2={(A, C, E)} for block P 22=(B, D, F): on x=0: next states: DBB blk indices: 222 Pb 20={(B, D, F)}=P 22 on x=1: next states: FFC blk indices: 221 Pb 21={(B, D), (F)} refine: P 22=P 22 • Pb 21= Pb 21 ={(B, D), (F)} P 2={(A, C, E), (B, D), (F)} ENEE 644 NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 A B C D E F D 1/1 A x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 0/0 1/0 0/0 F 0/0 1/1 E B 1/0 1/1 0/0 C 21
Example: Finding Equivalent States PS P 1={(A, C, E), (B, D, F)} P 2={(A, C, E)} for block P 22=(B, D, F): on x=0: next states: DBB blk indices: 222 Pb 20={(B, D, F)}=P 22 on x=1: next states: FFC blk indices: 221 Pb 21={(B, D), (F)} refine: P 22=P 22 • Pb 21= Pb 21 ={(B, D), (F)} P 2={(A, C, E), (B, D), (F)} ENEE 644 NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 A B C D E F D 1/1 A x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 0/0 1/0 0/0 F 0/0 1/1 E B 1/0 1/1 0/0 C 21
 Example: Finding Equivalent States P 1={(A, C, E), (B, D, F)} P 2={(A, C, E), (B, D), (F)} for block P 13=(A, C, E): on x=0: next states: EEC blk indices: 111 Pb 10={(A, C, E)}=P 13 on x=1: next states: DBF blk indices: 223 Pb 11={(A, C), (E)} refine: P 13=P 13 • Pb 11= Pb 13 ={(A, C), (E)} P 3={(A, C), (E)} PS NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 A B C D E F D 1/1 A 0/0 1/0 0/0 F 0/0 1/1 E ENEE 644 x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 B 1/0 1/1 0/0 C 22
Example: Finding Equivalent States P 1={(A, C, E), (B, D, F)} P 2={(A, C, E), (B, D), (F)} for block P 13=(A, C, E): on x=0: next states: EEC blk indices: 111 Pb 10={(A, C, E)}=P 13 on x=1: next states: DBF blk indices: 223 Pb 11={(A, C), (E)} refine: P 13=P 13 • Pb 11= Pb 13 ={(A, C), (E)} P 3={(A, C), (E)} PS NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 A B C D E F D 1/1 A 0/0 1/0 0/0 F 0/0 1/1 E ENEE 644 x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 B 1/0 1/1 0/0 C 22
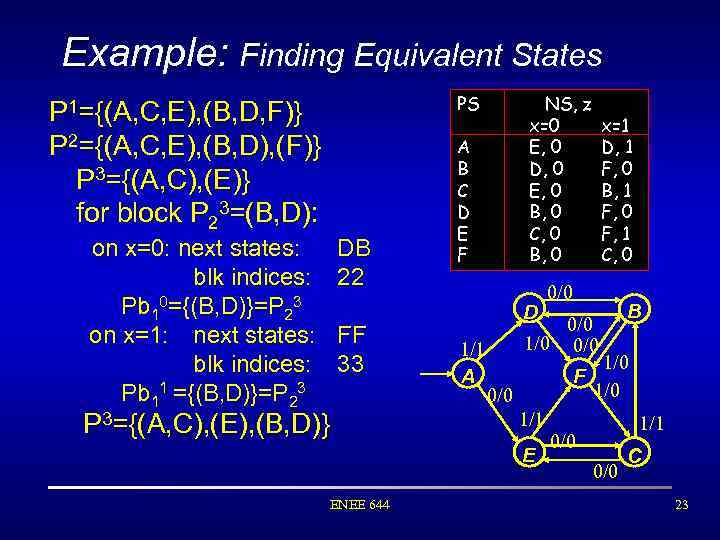 Example: Finding Equivalent States PS P 1={(A, C, E), (B, D, F)} P 2={(A, C, E), (B, D), (F)} P 3={(A, C), (E)} for block P 23=(B, D): on x=0: next states: blk indices: Pb 10={(B, D)}=P 23 on x=1: next states: blk indices: Pb 11 ={(B, D)}=P 23 DB 22 FF 33 P 3={(A, C), (E), (B, D)} NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 A B C D E F D 1/1 A 0/0 1/0 0/0 F 0/0 1/1 E ENEE 644 x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 B 1/0 1/1 0/0 C 23
Example: Finding Equivalent States PS P 1={(A, C, E), (B, D, F)} P 2={(A, C, E), (B, D), (F)} P 3={(A, C), (E)} for block P 23=(B, D): on x=0: next states: blk indices: Pb 10={(B, D)}=P 23 on x=1: next states: blk indices: Pb 11 ={(B, D)}=P 23 DB 22 FF 33 P 3={(A, C), (E), (B, D)} NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 A B C D E F D 1/1 A 0/0 1/0 0/0 F 0/0 1/1 E ENEE 644 x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 B 1/0 1/1 0/0 C 23
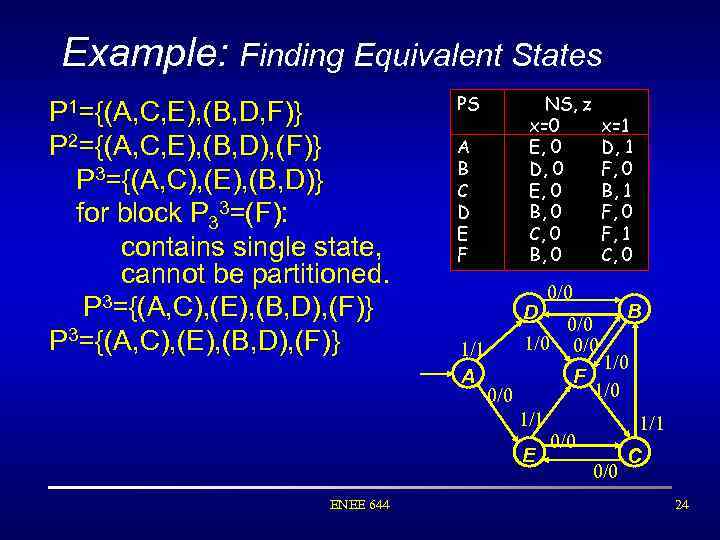 Example: Finding Equivalent States P 1={(A, C, E), (B, D, F)} P 2={(A, C, E), (B, D), (F)} P 3={(A, C), (E), (B, D)} for block P 33=(F): contains single state, cannot be partitioned. P 3={(A, C), (E), (B, D), (F)} PS NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 A B C D E F D 1/1 A 0/0 1/0 0/0 F 0/0 1/1 E ENEE 644 x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 B 1/0 1/1 0/0 C 24
Example: Finding Equivalent States P 1={(A, C, E), (B, D, F)} P 2={(A, C, E), (B, D), (F)} P 3={(A, C), (E), (B, D)} for block P 33=(F): contains single state, cannot be partitioned. P 3={(A, C), (E), (B, D), (F)} PS NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 A B C D E F D 1/1 A 0/0 1/0 0/0 F 0/0 1/1 E ENEE 644 x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 B 1/0 1/1 0/0 C 24
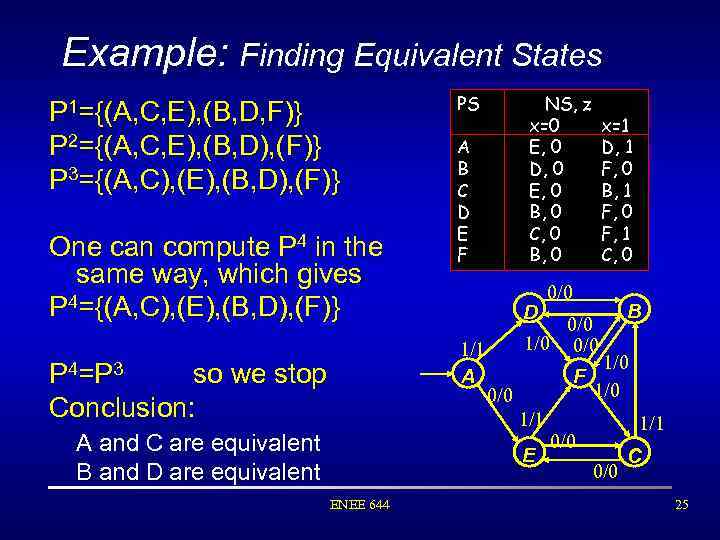 Example: Finding Equivalent States P 1={(A, C, E), (B, D, F)} P 2={(A, C, E), (B, D), (F)} P 3={(A, C), (E), (B, D), (F)} One can compute P 4 in the same way, which gives P 4={(A, C), (E), (B, D), (F)} PS A B C D E F D 1/1 A P 4=P 3 so we stop Conclusion: NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 F 0/0 E ENEE 644 0/0 1/0 0/0 1/1 A and C are equivalent B and D are equivalent x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 B 1/0 1/1 0/0 C 25
Example: Finding Equivalent States P 1={(A, C, E), (B, D, F)} P 2={(A, C, E), (B, D), (F)} P 3={(A, C), (E), (B, D), (F)} One can compute P 4 in the same way, which gives P 4={(A, C), (E), (B, D), (F)} PS A B C D E F D 1/1 A P 4=P 3 so we stop Conclusion: NS, z x=0 E, 0 D, 0 E, 0 B, 0 C, 0 B, 0 F 0/0 E ENEE 644 0/0 1/0 0/0 1/1 A and C are equivalent B and D are equivalent x=1 D, 1 F, 0 B, 1 F, 0 F, 1 C, 0 B 1/0 1/1 0/0 C 25
 FSM Minimization with Equivalent States STG: collapse states in the same equivalent class to one state; update edges. 0/0 D 1/0 1/1 A 0/0 F 0/0 D 1/1 1/0 A 1/0 1/1 E 0/0 B 1/1 0/0 C 0/0 0/0 1/0 1/1 0/0 E F B 1/0 1/1 0/0 C Equivalent classes: (A, C), (B, D), (E), (F) ENEE 644 26
FSM Minimization with Equivalent States STG: collapse states in the same equivalent class to one state; update edges. 0/0 D 1/0 1/1 A 0/0 F 0/0 D 1/1 1/0 A 1/0 1/1 E 0/0 B 1/1 0/0 C 0/0 0/0 1/0 1/1 0/0 E F B 1/0 1/1 0/0 C Equivalent classes: (A, C), (B, D), (E), (F) ENEE 644 26
 Definition: Finite State Machine Recall: A Finite State Machine (FSM) of Mealy type is a 6 tuple
Definition: Finite State Machine Recall: A Finite State Machine (FSM) of Mealy type is a 6 tuple
 FSM Equivalence Checking M 1= M 2= > What do we mean by M 1 and M 2 are equivalent? For any input, they should produce the same output. = I 1 = I 2 = O 1 = O 2 > How to verify that M 1 and M 2 are equivalent? = Assuming that S 01={s 01} and S 02={s 02}, then if there is no input string can distinguish s 01 and s 02, we claim that M 1 and M 2 are equivalent. ENEE 644 28
FSM Equivalence Checking M 1= M 2= > What do we mean by M 1 and M 2 are equivalent? For any input, they should produce the same output. = I 1 = I 2 = O 1 = O 2 > How to verify that M 1 and M 2 are equivalent? = Assuming that S 01={s 01} and S 02={s 02}, then if there is no input string can distinguish s 01 and s 02, we claim that M 1 and M 2 are equivalent. ENEE 644 28
 The Product Machine > The product machine of two FSMs, M 1=
The Product Machine > The product machine of two FSMs, M 1=
 Run and Reachable State > For an FSM M 1=, an input string x 0 x 1…xk-1 produces a sequence of states s 0 s 1…sk (called a run, where s 0 is the starting state) and an output string z 0 z 1…zk-1. > A state t is reachable from state s if there exists an input string that produces a run with s as the starting state and t as the ending state. > The reachable states of an FSM
Run and Reachable State > For an FSM M 1=, an input string x 0 x 1…xk-1 produces a sequence of states s 0 s 1…sk (called a run, where s 0 is the starting state) and an output string z 0 z 1…zk-1. > A state t is reachable from state s if there exists an input string that produces a run with s as the starting state and t as the ending state. > The reachable states of an FSM
 FSM Equivalence Checking M 1= M 2= > If I 1 I 2 or O 1 O 2 return not equivalent; > Build the product machine M 12; > Start with the initial state s 012, traverse the STG of the FSM M 12; = For each reachable state in M 12, if it can output 0, return not equivalent; = Return equivalent; > To get a distinguishing sequence in the case of not equivalent, we need to store the predecessor information and do backtracking. ENEE 644 31
FSM Equivalence Checking M 1= M 2= > If I 1 I 2 or O 1 O 2 return not equivalent; > Build the product machine M 12; > Start with the initial state s 012, traverse the STG of the FSM M 12; = For each reachable state in M 12, if it can output 0, return not equivalent; = Return equivalent; > To get a distinguishing sequence in the case of not equivalent, we need to store the predecessor information and do backtracking. ENEE 644 31
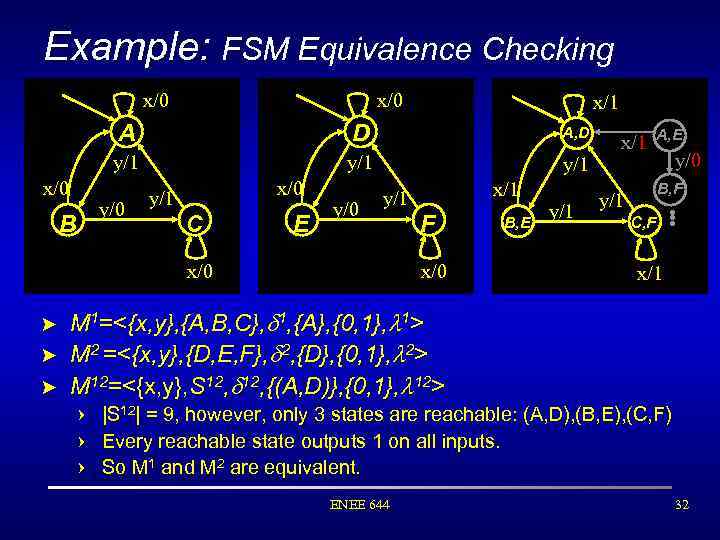 Example: FSM Equivalence Checking x/0 x/1 A A, D y/1 x/0 D y/1 y/0 B x/0 y/1 C E y/0 x/1 y/1 x/0 F x/0 B, E y/1 x/1 y/1 A, E y/0 B, F C, F • • • x/0 x/1 > M 1=<{x, y}, {A, B, C}, 1, {A}, {0, 1}, 1> > M 2 =<{x, y}, {D, E, F}, 2, {D}, {0, 1}, 2> > M 12=<{x, y}, S 12, {(A, D)}, {0, 1}, 12> = = = |S 12| = 9, however, only 3 states are reachable: (A, D), (B, E), (C, F) Every reachable state outputs 1 on all inputs. So M 1 and M 2 are equivalent. ENEE 644 32
Example: FSM Equivalence Checking x/0 x/1 A A, D y/1 x/0 D y/1 y/0 B x/0 y/1 C E y/0 x/1 y/1 x/0 F x/0 B, E y/1 x/1 y/1 A, E y/0 B, F C, F • • • x/0 x/1 > M 1=<{x, y}, {A, B, C}, 1, {A}, {0, 1}, 1> > M 2 =<{x, y}, {D, E, F}, 2, {D}, {0, 1}, 2> > M 12=<{x, y}, S 12, {(A, D)}, {0, 1}, 12> = = = |S 12| = 9, however, only 3 states are reachable: (A, D), (B, E), (C, F) Every reachable state outputs 1 on all inputs. So M 1 and M 2 are equivalent. ENEE 644 32
 Example: FSM Equivalence Checking x/0 x/1 A B A, D y/1 x/0 D y/1 y/0 x/0 y/1 C E y/0 x/1 y/1 x/1 F x/0 B, E y/1 x/1 A, E y/0 B, F y/1 C, F • • • x/0 > Now, M 1 and M 2 are not equivalent. > Consequently, one of the reachable state (C, F) outputs 0 on input x. > Backtracking to find the distinguishing sequence. ENEE 644 33
Example: FSM Equivalence Checking x/0 x/1 A B A, D y/1 x/0 D y/1 y/0 x/0 y/1 C E y/0 x/1 y/1 x/1 F x/0 B, E y/1 x/1 A, E y/0 B, F y/1 C, F • • • x/0 > Now, M 1 and M 2 are not equivalent. > Consequently, one of the reachable state (C, F) outputs 0 on input x. > Backtracking to find the distinguishing sequence. ENEE 644 33


