44f867f5d7de82f5361d84cb952cf2e4.ppt
- Количество слайдов: 91

September 7, 2000 Language and Information Handout #1 (C) 2000, The University of Michigan 1

Course Information • • • Instructor: Dragomir R. Radev (radev@si. umich. edu) Office: 305 A, West Hall Phone: (734) 615 -5225 Office hours: TTh 3 -4 Course page: http: //www. si. umich. edu/~radev/760 Class meets on Thursdays, 5 -8 PM in 311 West Hall (C) 2000, The University of Michigan 2
Introduction (C) 2000, The University of Michigan 3

Demos • • Google Ask. Jeeves One. Across Systran (C) 2000, The University of Michigan 4

Some Statistics • • Business e-mail sent per day in the US: 2. 1 Billion Spam per day: 7 Billion First class mail per year: 107 Billion Text on Internet (2/99): > 6 TB indexed: 16% (Lawrence and Giles, Nature 400, 1999) Dialog (www. dialog. com): 9 TB Average college library: 1 TB More statistics: http: //www. cyberatlas. internet. com (C) 2000, The University of Michigan 5

Languages • Languages: 39, 000 languages and dialects (22, 000 dialects in India alone) • Top languages: Chinese/Mandarin (885 M), Spanish (332 M), English (322 M), Bengali (189 M), Hindi (182 M), Portuguese (170 M), Russian (170 M), Japanese (125 M) • Source: www. sil. org/ethnologue, www. nytimes. com • Internet: English (128 M), Japanese (19. 7 M), German (14 M), Spanish (9. 4 M), French (9. 3 M), Chinese (7. 0 M) • Usage: English (1999 -54%, 2001 -51%, 2003 -46%, 200543%) • Source: www. computereconomics. com (C) 2000, The University of Michigan 6

Syllabus • Introduction to the course and linguistic background – The study of language. Computational Linguistics and Psycholinguistics. • Elementary probability and statistics – Describing data. Measures of central tendency. The z score. Hypothesis testing. • Information theory – Entropy, joint entropy, conditional entropy. Relative entropy and mutual information. Chain rules. • Data compression and coding – Entropy rate. Language modeling. Examples of codes. Optimal codes. Huffman codes. Arithmetic coding. The entropy of English. (C) 2000, The University of Michigan 7

Syllabus • Clustering – Cluster analysis. Clustering of terms according to semantic similarity. Distributional clustering. • Concordancing and collocations – Concordances. Collocations. Syntactic criteria for collocability. • Literary detective work – The statistical analysis of writing style. Decipherment and translation. • Information extraction – Message understanding. Trainable methods. • Word sense disambiguation and lexical acquisition – Supervised disambiguation. Unsupervised disambiguation. Attachment ambiguity. Computational lexicography. (C) 2000, The University of Michigan 8
![Syllabus • Part-of-speech tagging [*] – Statistical taggers. Transformation-based learning of tags. Maximum entropy Syllabus • Part-of-speech tagging [*] – Statistical taggers. Transformation-based learning of tags. Maximum entropy](https://present5.com/presentation/44f867f5d7de82f5361d84cb952cf2e4/image-9.jpg)
Syllabus • Part-of-speech tagging [*] – Statistical taggers. Transformation-based learning of tags. Maximum entropy models. Weighted finite-state transducers. • Question answering – Semantic representation. Predictive annotation. • Text summarization – Single-document summarization. Multi-document summarization. Language models. Maximal Marginal Relevance. Cross-document structure theory. Trainable methods. Text categorization. • Other topics – Text alignment. Word alignment. Statistical machine translation. Discourse segmentation. Text categorization. Maximum entropy modeling. (C) 2000, The University of Michigan 9

Assignments • Problem sets – The assignments will involve analysis of Web-based data using both manual and automated techniques • Project – Data analysis and/or programming involved • Midterm – A mixture of short-answer and essay-type questions • Final – A mixture of short-answer and essay-type questions (C) 2000, The University of Michigan 10

Projects Each student will be responsible for designing and completing a research project that demonstrates the ability to use concepts from the class in addressing a practical problem for humanities computing. A significant part of the final grade will depend on the project assignment. Students will need to submit a project proposal, a progress report, and the project itself. Students can elect to do a project on an assigned topic, or to select a topic of their own. The final version of the project will be put on the World Wide Web, and will be defended in front of the class at the end of the semester (procedure TBA). In some cases (and only with instructor’s approval), students may be allowed to work in pairs, e. g. , students with different backgrounds may collaborate on a larger project. (C) 2000, The University of Michigan 11

Readings • Textbook: – Oakes, Chapter 1, pages 1 – 10, 24 – 35 • Additional readings – M&S, Chapter 2, pages 39 – 54 – M&S, Chapter 3, pages 81 – 113 (C) 2000, The University of Michigan 12

Computational Linguistics (C) 2000, The University of Michigan 13
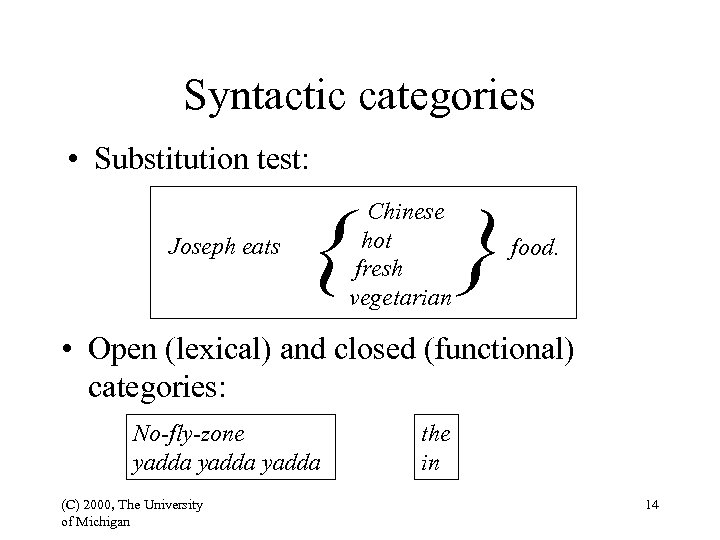
Syntactic categories • Substitution test: Joseph eats { Chinese hot fresh vegetarian } food. • Open (lexical) and closed (functional) categories: No-fly-zone yadda (C) 2000, The University of Michigan the in 14

Morphology The dog chased the yellow bird. • • • Parts of speech: eight (or so) general types Inflection (number, person, tense…) Derivation (adjective-adverb, noun-verb) Compounding (separate words or single word) Part-of-speech tagging Morphological analysis (prefix, root, suffix, ending) (C) 2000, The University of Michigan 15

Part of Speech Tags From Church (1991) - 79 tags NN IN AT NP JJ , NNS CC RB VB VBN VBD CS /* /* /* /* singular noun */ preposition */ article */ proper noun */ adjective */ comma */ plural noun */ conjunction */ adverb */ un-inflected verb */ verb +en (taken, looked (passive, perfect)) */ verb +ed (took, looked (past tense)) */ subordinating conjunction */ (C) 2000, The University of Michigan 16
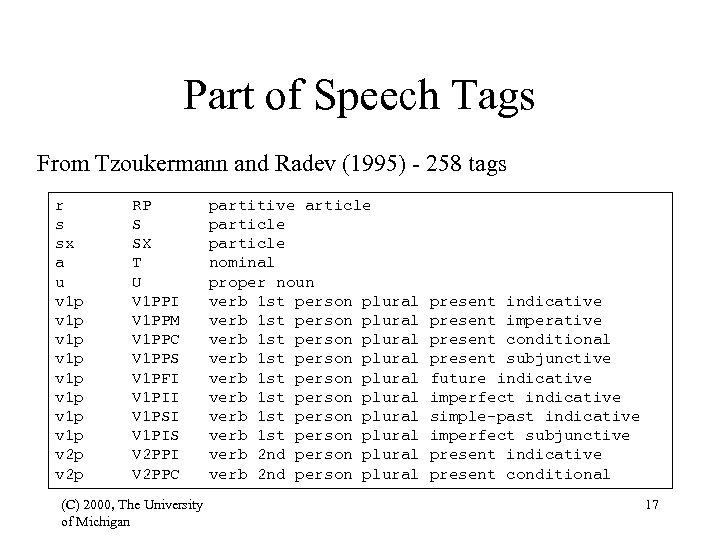
Part of Speech Tags From Tzoukermann and Radev (1995) - 258 tags r s sx a u v 1 p v 1 p v 2 p RP S SX T U V 1 PPI V 1 PPM V 1 PPC V 1 PPS V 1 PFI V 1 PII V 1 PSI V 1 PIS V 2 PPI V 2 PPC (C) 2000, The University of Michigan partitive article particle nominal proper noun verb 1 st person plural verb 1 st person plural verb 2 nd person plural present indicative present imperative present conditional present subjunctive future indicative imperfect indicative simple-past indicative imperfect subjunctive present indicative present conditional 17

Jabberwocky (Lewis Carroll) `Twas brillig, and the slithy toves Did gyre and gimble in the wabe: All mimsy were the borogoves, And the mome raths outgrabe. "Beware the Jabberwock, my son! The jaws that bite, the claws that catch! Beware the Jubjub bird, and shun The frumious Bandersnatch!" (C) 2000, The University of Michigan 18

Nouns • Nouns: dog, tree, computer, idea • Nouns vary in number (singular, plural), gender (masculine, feminine, neuter), case (nominative, genitive, accusative, dative) • Latin: filius (m), filia (f), filium (object) German: Mädchen • Clitics (‘s) (C) 2000, The University of Michigan 19

Pronouns • Pronouns: she, ourselves, mine • Pronouns vary in person, gender, number, case (in English: nominative, accusative, possessive, 2 nd possessive, reflexive) Joe bought him an ice cream. Joe bought himself an ice cream. • Anaphors: herself, each other (C) 2000, The University of Michigan 20

Determiners and Adjectives • • Articles: the, a Demonstratives: this, that Adjectives: describe properties Attributive and predicative adjectives Agreement: in gender, number Comparative and superlative (derivative and periphrastic) Positive form (C) 2000, The University of Michigan 21

Verbs • • • Actions, activities, and states (throw, walk, have) English: four verb forms tenses: present, past, future other inflection: number, person gerunds and infinitive aspect: progressive, perfective voice: active, passive participles, auxiliaries irregular verbs French and Finnish: many more inflections than English (C) 2000, The University of Michigan 22

Other Parts of Speech • • • Adverbs, prepositions, particles phrasal verbs (the plane took off, take it off) particles vs. prepositions (she ran up a bill/hill) Coordinating conjunctions: and, or, but Subordinating conjunctions: if, because, that, although • Interjections: Ouch! (C) 2000, The University of Michigan 23

Phrase-structure Grammars Alice bought Bob flowers. Bob bought Alice flowers. • • Constituent order (SVO, SOV) imperative forms sentences with auxiliary verbs interrogative sentences declarative sentences start symbol and rewrite rules context-free view of language (C) 2000, The University of Michigan 24

Sample Phrase-structure Grammar S NP NP NP VP VP VP P NP AT AT NP VP VBD IN (C) 2000, The University of Michigan VP NNS NN PP PP NP NP AT NNS NNS VBD VBD IN IN NN the drivers teachers lakes drank ate saw in of cake 25

Phrase-structure Grammars • Local dependencies • Non-local dependencies • Subject-verb agreement The students who wrote the best essays were given a reward. • wh-extraction Should Derek read a magazine? Which magazine should Derek read? • Empty nodes (C) 2000, The University of Michigan 26

Dependency: Arguments and Adjuncts Sally watched the kids in the car. • • • Event + dependents (verb arguments are usually NPs) agent, patient, instrument, goal - semantic roles subject, direct object, indirect object transitive, intransitive, and ditransitive verbs active and passive voice (C) 2000, The University of Michigan 27

Phrase Structure Ambiguity • • Grammars are used for generating and parsing sentences Parses Syntactic ambiguity Attachment ambiguity: Visiting relatives can be boring. The children ate the cake with a spoon. High vs. low attachment Garden path sentences: The horse raced past the barn fell. Is the book on the table red? (C) 2000, The University of Michigan 28

Ungrammaticality vs. Semantic Abnormality * Slept children the. # Colorless green ideas sleep furiously. # The cat barked. (C) 2000, The University of Michigan 29

Semantics and Pragmatics • Lexical semantics and compositional semantics • Hypernyms, hyponyms, antonyms, meronyms and holonyms (part-whole relationship, tire is a meronym of car), synonyms, homonyms • Senses of words, polysemous words • Homophony (bass). • Collocations: white hair, white wine • Idioms: to kick the bucket (C) 2000, The University of Michigan 30

Discourse Analysis • Anaphoric relations: 1. Mary helped Peter get out of the car. He thanked her. 2. Mary helped the other passenger out of the car. The man had asked her for help because of his foot injury. • Information extraction problems (entity crossreferencing) Hurricane Hugo destroyed 20, 000 Florida homes. At an estimated cost of one billion dollars, the disaster has been the most costly in the state’s history. (C) 2000, The University of Michigan 31

Pragmatics • The study of how knowledge about the world and language conventions interact with literal meaning. • Speech acts • Research issues: resolution of anaphoric relations, modeling of speech acts in dialogues (C) 2000, The University of Michigan 32

Other Research Areas • Linguistics is traditionally divided into phonetics, phonology, morphology, syntax, semantics, and pragmatics. • Sociolinguistics: interactions of social organization and language. • Historical linguistics: change over time. • Linguistic typology • Language acquisition • Psycholinguistics: real-time production and perception of language (C) 2000, The University of Michigan 33

Ambiguities in Natural Language • address, resent, entrance, number • Lee: Wait to buy IBM (http: //cnnfn. cnn. com/2000/07/19/investing/q_talking_stocks/) • Pfizer to buy Warner-Lambert in $90 -billion deal (http: //detnews. com/2000/business/0002/07/02080007. htm) (C) 2000, The University of Michigan 34

My Research Interests • Text summarization (especially, of multiple documents) • Text categorization and clustering • Information extraction • Question answering (C) 2000, The University of Michigan 35

Main Research Forums • Conferences: ACL, SIGIR, ANLP, Coling, EACL/NAACL, AMTA/MT Summit, ICSLP/Eurospeech • Journals: Computational Linguistics, Natural Language Engineering, Information Retrieval, Information Processing and Management, ACM Transactions on Information Systems • University centers: Columbia, CMU, UMass, MIT, UPenn, USC/ISI, NMSU, Brown, Michigan, Maryland, Edinburgh, Cambridge, Saarbrücken, Kyoto, and many others • Industrial research sites: AT&T, Bell Labs, IBM, Xerox PARC, SRI, BBN/GTE, MITRE, Microsoft • Startups: Nuance, Ask. com, Inxight (C) 2000, The University of Michigan 36

Mathematical Foundations (C) 2000, The University of Michigan 37

Probability Spaces • Probability theory: predicting how likely it is that something will happen • basic concepts: experiment (trial), basic outcomes, sample space • discrete and continuous sample spaces • for NLP: mostly discrete spaces • events • is the certain event while is the impossible event • event space - all possible events (C) 2000, The University of Michigan 38

Probability Spaces • Probabilities: numbers between 0 and 1 • Probability function (distribution): distributes a probability mass of 1 throughout the sample space . • Example: coin is tossed three times. What is the probability of 2 heads? • Uniform distribution (C) 2000, The University of Michigan 39

Conditional Probability and Independence • Prior and posterior probability P(A|B) = P(A B) P(B) A B (C) 2000, The University of Michigan 40

Conditional Probability and Independence • The chain rule: n-1 P(A 1 … An) = P(A 1) P(A 2 |A 1) P(A 3|A 1 A 2 ) … P(An | Ai) i=1 • This rule is used in many ways in statistical NLP more specifically in Markov Models. • Two events are independent when P(A B) = P(A)P(B) • Unless P(B)=0 this is equivalent to saying that P(A) = P(A|B) • If two events are not independent, they are considered dependent (C) 2000, The University of Michigan 41

Bayes’ Theorem • Bayes’ theorem is used to calculate P(A|B) given P(B|A) = (C) 2000, The University of Michigan P(B A) P(B) = P(A|B)P(B) P(A) 42

Random Variables • Simply a function: X: Rn • The numbers are generated by a stochastic process with a certain probability distribution. • Example: the discrete random variable X that is the sum of the faces of two randomly thrown dice. • Probability mass function (pmf) which gives the probability that the random variable has different numeric values: P(x) = P(X = x) = P(Ax) where Ax = { : X( ) = x} (C) 2000, The University of Michigan 43

Random Variables • If a random variable X is distributed according to the pmf p(x), the we write X ˜ p(x) • For a discrete random variable, we have that: p(xi) = P(Axi) = P( ) = 1 (C) 2000, The University of Michigan 44

Expectation and Variance • Expectation = mean (average) of a random variable. • If X is a random variable with a pmf p(x), such that |x| p(x) < , then the expectation is: E(X) = xp(x) • Example: rolling one die • Variance = measure of whether the values of the random variable tend to be consistent over trials or to vary a lot. Var(X) = E((X - E(X))2) = E(X 2) - E 2(X) • Standard deviation = square root of variance (C) 2000, The University of Michigan 45

Expectation and Variance • Composition of functions: E(g(Y)) = g(y)p(y) • Examples: If g(Y) = a. Y + b, then E(g(Y)) = a. E(Y) + b E(X+Y) = E(X) + E(Y) E(XY) = E(X)E(Y), if X and Y are independent (C) 2000, The University of Michigan 46

Joint and Conditional Distributions • Joint (multivariate) probability distributions: p(x, y) = P(X = x , Y = y) • Marginal pmf: px(x) = yp(x, y) p. Y(y) = xp(x, y) • If X and Y are independent: p(x, y) = p. X(x)p. Y(y) (C) 2000, The University of Michigan 47

Joint and Conditional Distributions • Conditional pmf in terms of the joint distribution: p. X|Y(x|y) = (C) 2000, The University of Michigan P(x, y) p. Y(y) for y such that p. Y(y) > 0 48

Determining P • • Estimation Example “The cow chewed its cud” Relative frequency Parametric approach (doesn’t work for distribution of words in newspaper articles in a particular topic category) • Non-parametric approach (C) 2000, The University of Michigan 49

The Binomial Distribution • The number r of successes out of n trials given that the probability of success in any single trial is p: B(r; n, p) = n r ( ) pr (1 -p)n-r, where n r ( ) n! = (n-r)!r! • Example: tossing a (possibly weighted) coin n times. (C) 2000, The University of Michigan 50
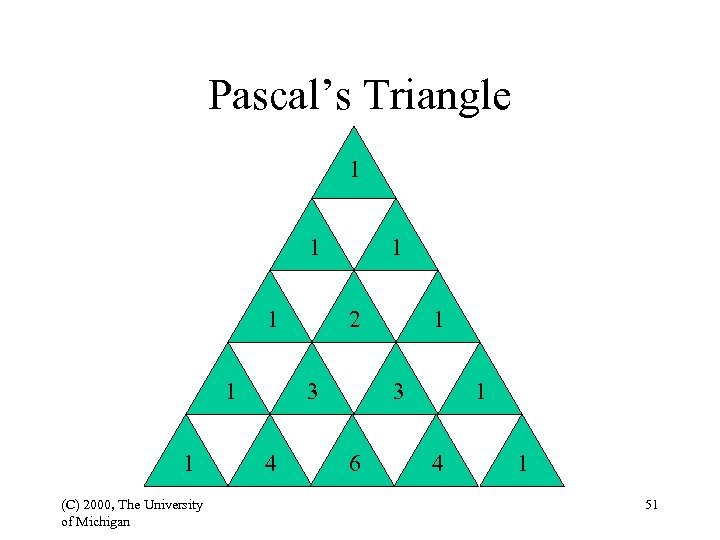
Pascal’s Triangle 1 1 1 (C) 2000, The University of Michigan 1 2 3 4 1 3 6 1 4 1 51

The Normal Distribution • Describes a continuous distribution n(x; m, s) = 1 2 p -(x-m)2/(2 2) e • Standard normal distribution: when = 0 and = 1 • In statistics, normal distribution is often used to approximate the binomial distribution. It should only be used when np(1 -p) > 5 • In NLP, such assumptions are unwise. Example: “shade tree mechanics” (C) 2000, The University of Michigan 52

Statistics for Corpus Linguistics (C) 2000, The University of Michigan 53

Statistics for Corpus Linguistics • Descriptive statistics: how to describe data • Describing relationships: the Chi-square test, correlation, regression • Information theory: information, entropy, coding, redundancy, optimal codes, mutual information (C) 2000, The University of Michigan 54

Measures of Central Tendency • Mode: the most frequent score in a data set • Median: central score of the distribution • Mean: average of all scores (C) 2000, The University of Michigan 55

Examples • Split “Moby Dick” into 135 files (“pages”). • Occurrences of the word “the” in the first 15 pages: Data: 17 125 99 300 80 36 43 65 78 259 62 36 40 120 45 Mean: 93. 67 Median: 65 Mode: 36 (C) 2000, The University of Michigan 56

Probabilities • p = a/n, where a is the number of successes, and n is the number of trials. the sum of all probabilities is 1: p (i) = 1 • Independent probabilities (product of probabilities): P(a AND b) = P(a) * P(b) (C) 2000, The University of Michigan 57

Binomial Coefficient ( n ) = n!/r!(n-r)! r The probability of success in a single trial is: ( n r n-r )p q r where q = 1 - p (C) 2000, The University of Michigan 58

Related Concepts • For binomial distributions: – standard deviation is the square root of n, p, and q – mean is nxp • Normal distributions: – same as binomial, for large values of n – asymptotical bell curves (C) 2000, The University of Michigan 59

Skewed Normal Distributions • Positively skewed (most of the data is below the mean) • Negatively skewed (the opposite) • Bimodal distributions • In corpus analysis: the number of letters in a word or the length of a verse in syllables is usually positively skewed • Lognormal distributions (C) 2000, The University of Michigan 60

Central Limit Theorem When samples are repeatedly drawn from a population, the means of the samples are normally distributed around the population mean. This occurs whether or not the actual distribution is normal or not. (C) 2000, The University of Michigan 61

Measures of Variability • Variance = (x- ) /N-1 2 • Range • Standard deviation is the square root of the variance • Semi inter-quartile range (25%-75% range): Columbia ACT scores (26 -30) Data: 17 125 99 300 80 36 43 65 78 259 62 36 40 120 45 Mean: 93. 67 Median: 65 Variance: 6729. 52 Standard Deviation: 82. 03 (C) 2000, The University of Michigan 62

z-score • A measure of how far a value is from the mean, in terms of standard deviations • Example: = 93, = 82. Let’s consider a page with 144 occurrences of the word “the”. The zscore for that page is: z = (144 -93)/82 = 0. 62 • Using the table on pages 258 -259 of Oakes, we find that the new page is at the 26 th percentile (C) 2000, The University of Michigan 63

Hypothesis Testing • If two data sets are both normally distributed, and the means and standard deviations are known • Example: Francis and Kucera reported that the mean sentence length in government documents is 25. 48 words, while in the Present-Day Edited American English corpus, the mean length is 19. 27 words only (C) 2000, The University of Michigan 64

Hypotheses • Null hypothesis: that the difference can be explained in terms of chance and natural variability • Statistical significance: when there is less than 5% chance that the null hypothesis holds (C) 2000, The University of Michigan 65

T-testing • Tests the difference between two groups for normally-distributed interval data • The t-test is normally used with small samples: less than 30 items • The one-sample study compares a sample mean with an established population Tobs = (x - ) / stderr (C) 2000, The University of Michigan 66

Example 1 • Mixed corpus: 2. 5 verbs per sentence with 1. 2 standard deviation • Scientific corpus: 3. 5 verbs per sentence with 1. 6 standard deviation • number of sentences in the scientific corpus: 100 • standard error in scientific corpus: 3. 5/10 • observed value of t = (3. 5 -2. 5)/0. 35 = 2. 86 (C) 2000, The University of Michigan 67

Example 1 (Cont’d) • • Number of degrees of freedom: in the example: 99 Use table on page 260 of Oakes Find value: 1. 671 The observed value of t is larger, therefore the null hypothesis can be rejected (C) 2000, The University of Michigan 68

Tests for Difference Tobs = (x 1 - x 2) / stderr 2 = s 12/n 1 + s 22/n 2 (C) 2000, The University of Michigan 69
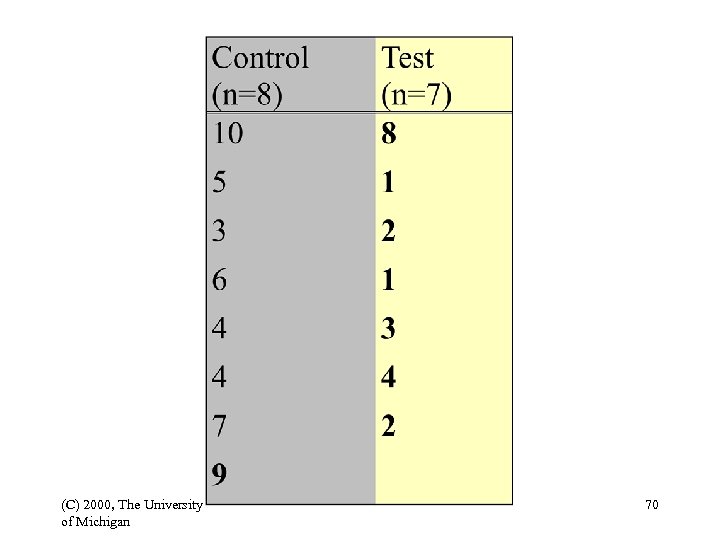
(C) 2000, The University of Michigan 70
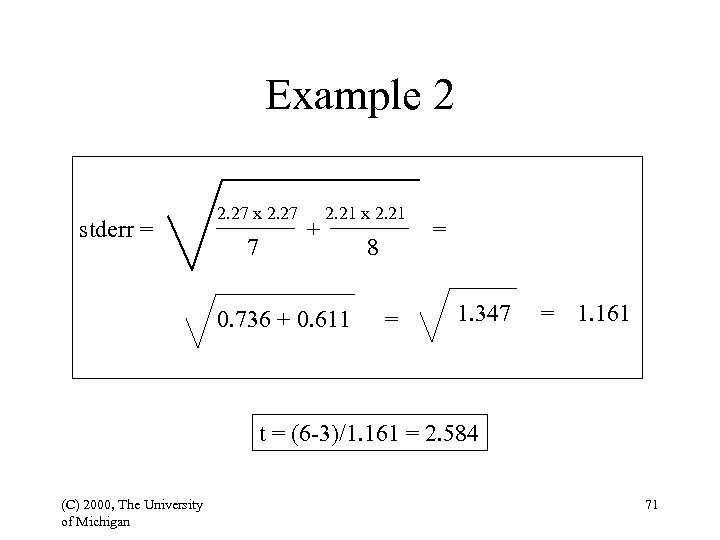
Example 2 stderr = 2. 27 x 2. 27 7 + 2. 21 x 2. 21 0. 736 + 0. 611 8 = = 1. 347 = 1. 161 t = (6 -3)/1. 161 = 2. 584 (C) 2000, The University of Michigan 71

Example 2 (Cont’d) • Number of degrees of freedom: 7 + 8 - 2 = 13 • critical value of significance at the 5 per cent level is 2. 16 • Since the observed value is greater than 2. 16, we can reject the null hypothesis (C) 2000, The University of Michigan 72

Parametric and Non-parametric Tests • Four scales of measurement: ratio, interval, ordinal, nominal • parametric tests (e. g. , t-test): interval or ratioscored dependent variables; assumes independent observations; usually normal distributions only • non-parametric tests: mostly for frequencies and rank-ordered scales; any type of distributions; less powerful than parametric tests (C) 2000, The University of Michigan 73

Chi-square Test • Relationship between the frequencies in a display table • Null hypothesis: no difference in distribution (all distributions are equal) 2 = (C) 2000, The University of Michigan (O-E)2 E 74

Special cases • When the number of degrees of freedom is 1, as in a 2 x 2 contingency table, Yates’s correction factor is used. • If O > E, add 0. 5 to O, otherwise, subtract 0. 5 from O. • If E < 5, results are not reliable. (C) 2000, The University of Michigan 75
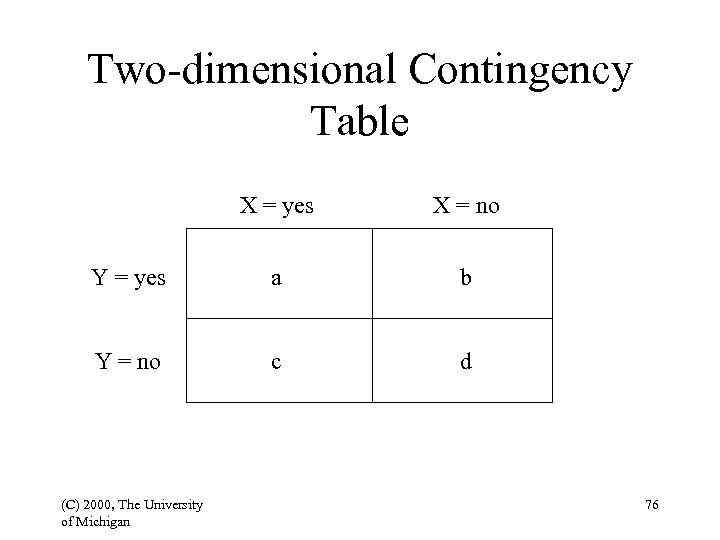
Two-dimensional Contingency Table X = yes X = no Y = yes a b Y = no c d (C) 2000, The University of Michigan 76
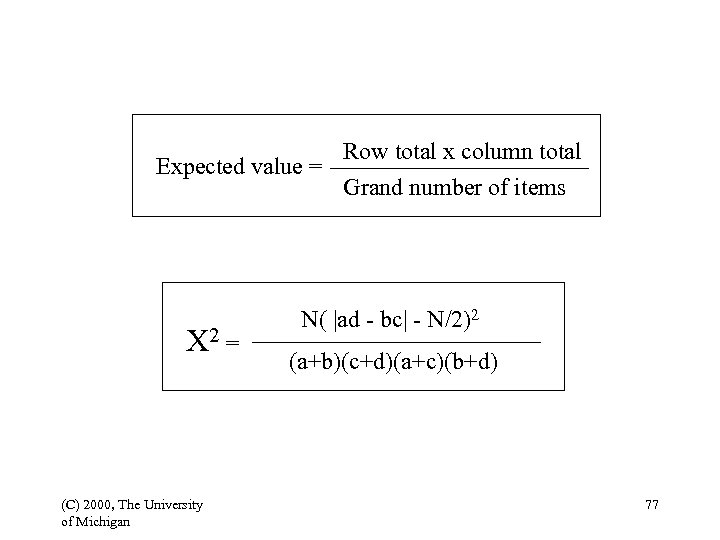
Row total x column total Expected value = Grand number of items 2 = (C) 2000, The University of Michigan N( |ad - bc| - N/2)2 (a+b)(c+d)(a+c)(b+d) 77
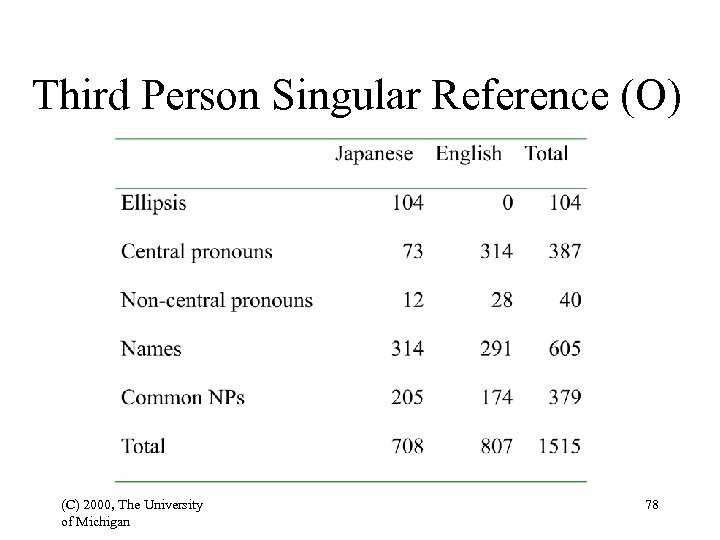
Third Person Singular Reference (O) (C) 2000, The University of Michigan 78
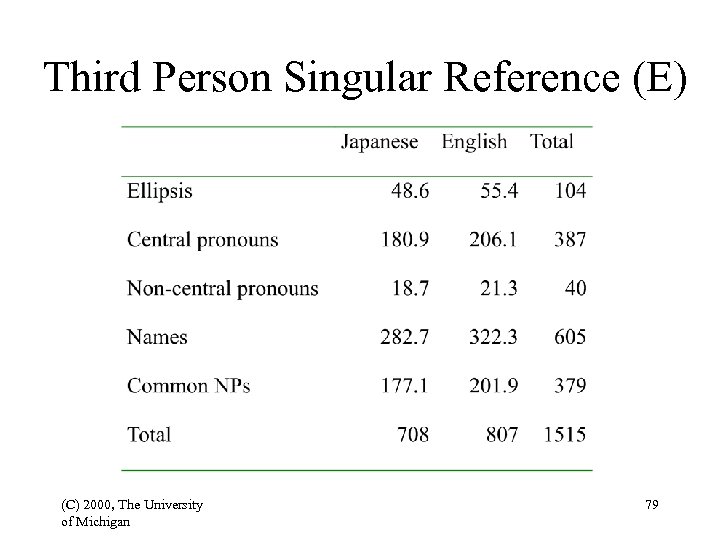
Third Person Singular Reference (E) (C) 2000, The University of Michigan 79

(O-E)2/E for the Two Languages S = 258. 8; df = (5 -1) x (2 -1) = 4 (C) 2000, The University of Michigan --> different at the 0. 001 level 80

Rank Correlation • Pearson - continuous data • Spearman’s rank correlation coefficient non-continuous variables r=1 - (C) 2000, The University of Michigan 6 Sd 2 N (N 2 - 1) 81
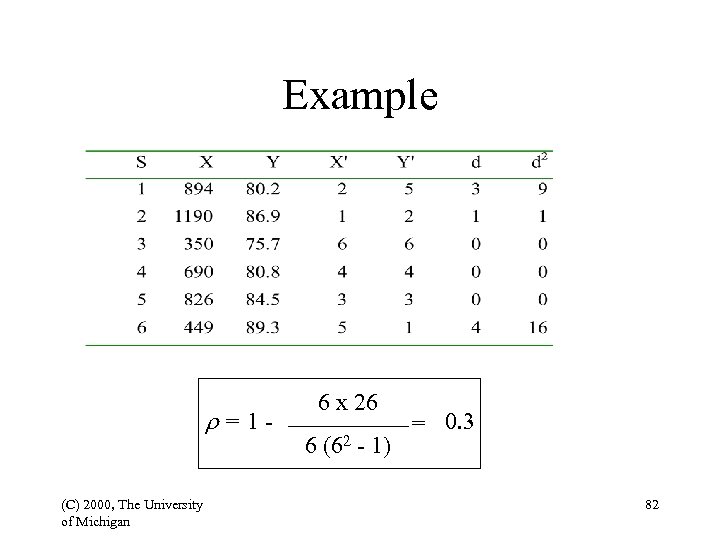
Example r=1(C) 2000, The University of Michigan 6 x 26 6 (62 - 1) = 0. 3 82

Linear Regression • Dependent and independent variables • Regression: used to predict the behavior of the dependent variable • Needed: m. X, m. Y, X, b = slope of Y(X) b= NSXY - SXSY NSX 2 - (SX)2 (C) 2000, The University of Michigan Y’ = m. Y + b(X - m. X) 83
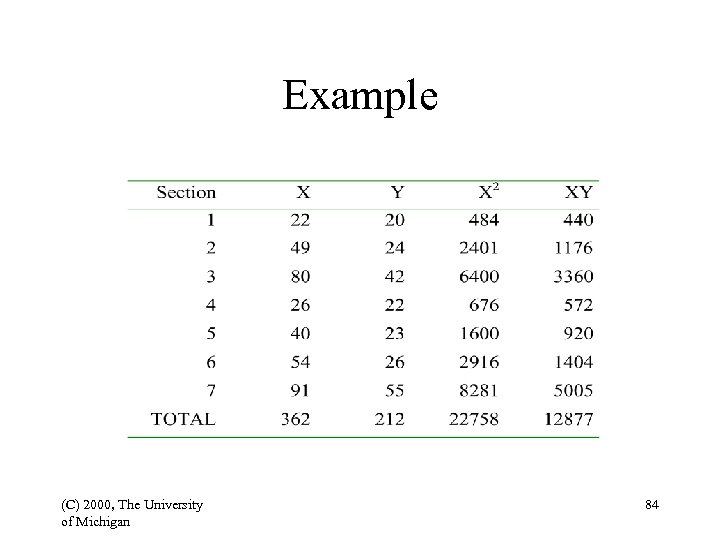
Example (C) 2000, The University of Michigan 84

Example (Cont’d) (7 x 12877) - (362 x 212) 90139 - 76744 a = 5. 775 13395 Y’ = 5. 775 + 0. 474 X b = (7 x 22758) - (362 x 362) = 159306 - 131044 = 28262 = 0. 474 (C) 2000, The University of Michigan 85
N-gram Models (C) 2000, The University of Michigan 86

Word Prediction • • • Example: “I’d like to make a collect …” “I have a gub” augmentative communication systems “He is trying to fine out” “Hopefully, all with continue smoothly in my absence” “They are leaving in about fifteen minuets to go to her house” • “I need to notified the bank of [this problem] • Language model: a statistical model of word sequences (C) 2000, The University of Michigan 87

Counting Words • Brown corpus (1 million words from 500 texts) • Example: “He stepped out into the hall, was delighted to encounter a water brother” - how many words? • Word forms and lemmas. “cat” and “cats” share the same lemma (also tokens and types) • Shakespeare’s complete works: 884, 647 word tokens and 29, 066 word types • Brown corpus: 61, 805 types and 37, 851 lemmas • American Heritage 3 rd edition has 200, 000 “boldface forms” (including some multiword phrases) (C) 2000, The University of Michigan 88

Unsmoothed N-grams • First approximation: each word has an equal probability to follow any other. E. g. , with 100, 000 words, the probability of each of them at any given point is. 00001 • “the” - 69, 971 times in BC, while “rabbit” appears 11 times • “Just then, the white …” P(w 1, w 2, …, wn) = P(w 1) P(w 2 |w 1) P(w 3|w 1 w 2) … P(wn |w 1 w 2…wn-1) Bigram model: Replace P(wn |w 1 w 2…wn-1) with P(wn|wn-1) (C) 2000, The University of Michigan 89

Markov Models • Assumption: we can predict the probability of some future item on the basis of a short history • Bigrams: first-level Markov models • Bigrammars: as an N-by-N matrix of probabilities, where N is the size of the vocabulary that we are modeling. (C) 2000, The University of Michigan 90
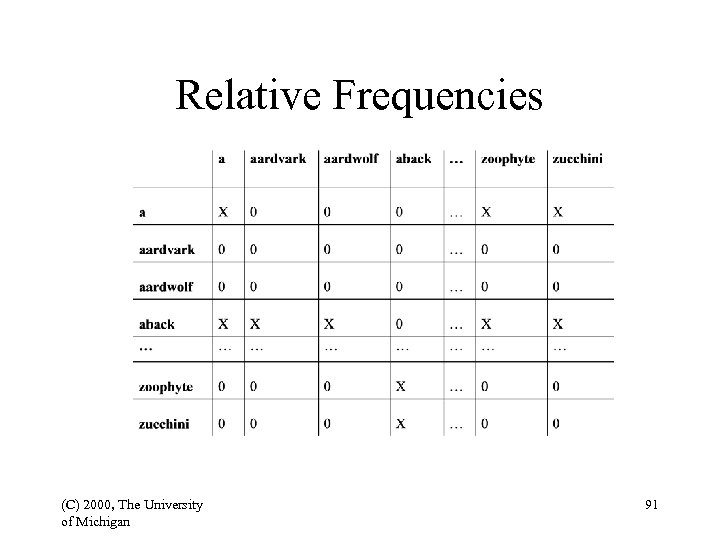
Relative Frequencies (C) 2000, The University of Michigan 91
44f867f5d7de82f5361d84cb952cf2e4.ppt