Sensitivity Analysis of Discrete Stochastic Systems Presented by

Sensitivity Analysis of Discrete Stochastic Systems Presented by : Tigran Mkrtchyan Master student of Saarland University 07. 06. 2013

Reminder : Sensitivity analysis Dependence of system behavior on the parameters Classical sensitivity analyses Discrete stochastic dynamical systems 2

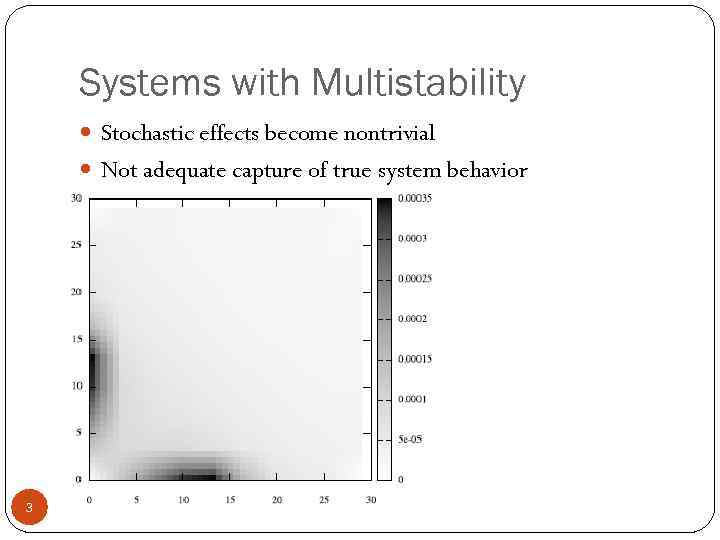
Systems with Multistability Stochastic effects become nontrivial Not adequate capture of true system behavior 3

Motivation Sensitivity Analyses for Discrete Stochastic Processes: Based on : Density function (distribution) sensitivity Uses: Classical Sensitivity + Fisher Information Matrix 4

Agenda 1) Introduction 2) Discrete Stochastic Sensitivity Measures 3) Sensitivity Analyses of CMEs 4) Example (Schlögl Model) 5) Conclusion 5

Introduction: Sensitivity coefficients A large sensitivity to a parameter suggests that the system’s performance (e. g. , temperature, reactor yield, periodicity) can drastically change with small variations in the parameter. 6

Introduction: Stochastic systems Outputs take random values. Evolve according to discrete-jump Markov processes. Density function can be constructed using the SSA 7

Introduction: The paper Develops parametric sensitivity analysis for discrete stochastic systems described by CMEs. Four sensitivity measures formulated based on: • direct extension of the deterministic sensitivity • Fisher Information Matrix (FIM) 8

Agenda 1) Introduction 2) Discrete Stochastic Sensitivity Measures 3) Sensitivity Analyses of CMEs 4) Example (Schlögl Model) 5) Conclusion 9

Analog § Sensitivity applied to the density function x - vector of states and outputs f - density function p - the vector of parameters 10

Sensitivity Measure 11

Sensitivity Coefficient (remarks) CME Random value of states Internal stochastic effects Low copy number of Molecules The probabilistic nature of the states arises from the uncertainty in the parameters. Computation of the coefficients has two approaches. 1. Fokker-Planck (yields a highly complex equation), 2. Authors’ use of a finite difference approach (yet to come). 12

Relation to the Score Function Gives the gradient of the log-likelihood function. Has a strong relevance in parameter estimation problems. 13

Fischer Information Matrix (FIM) Variance J describes the (maximum) information that can be extracted from (random) measurements to estimate the corresponding parameter values p: FIM defines the lower bound on the uncertainty in the parameter estimates according to the Cramer-Rao inequality 14

FIM –measure of sensitivity Assumes the density function follows a Gaussian distribution Under this assumption, the FIM reduces to: V− 1 denotes the measurement covariance 15

Wikipedia: FIM 16

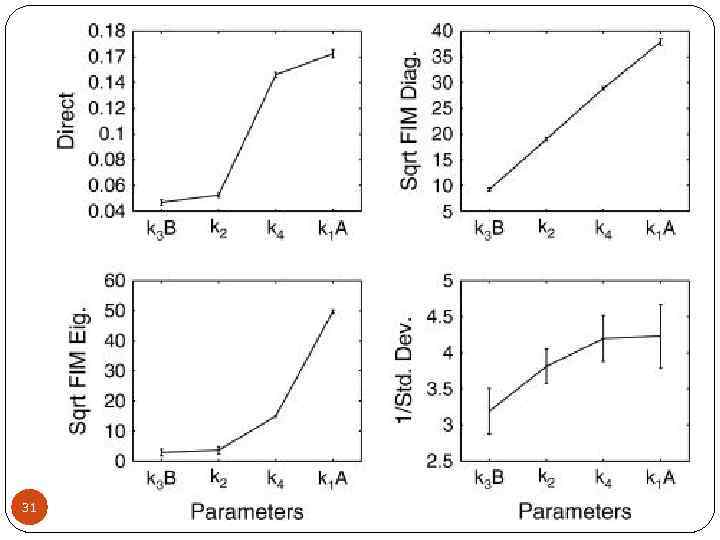
FIM - properties measure of information content, consolidation of (weighted) sensitivities the sensitivity matrix S is computed deterministically and the covariance V is obtained from stochastic simulations 17

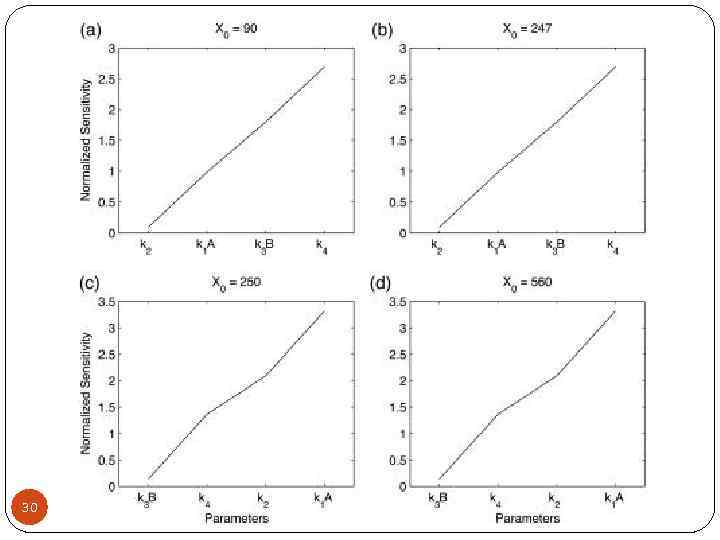
FIM : Three sensitivity measures The diagonal elements: represent the magnitudes of the sensitivities with respect to each individual parameter The eigenvalues: represent the magnitudes of the sensitivities with respect to simultaneous parameter variations. The diagonal elements of the matrix Vp are the square of the standard deviations of the parameters (A-optimality ) 18

Agenda 1) Introduction 2) Discrete Stochastic Sensitivity Measures 3) Sensitivity Analyses of CMEs 4) Example (Schlögl Model) 5) Conclusion 19

Reminder: CME ak - the propensity functions (probability of the kth reaction to occur between time t and t + dt, given the parameters p), νk - stoichiometric change in x when the kth reaction occurs, m - the total number of reactions 20

Sensitivity, Score Functions for CME Sj - stochastic sensitivity coefficient w. r. t jth parameter 21

Solving the equation As with the CME, the infinite dimensionality of the coupled sensitivity-CME differential equation makes its analytical solution difficult to construct. SSA cannot be directly applied to solve the sensitivity equation without loss of rigorous physical basis New approach: finite difference, to estimate the sensitivity coefficients below. 22

Construction Cumulative distribution function from the SSA realizations. which gives the density function f(x) as the derivative of F(x), 23

Estimating Stochastic Sensitivity & FIM Use centered difference approximation The perturbation Δpj : small enough to minimize truncation error, 2) large enough to avoid sensitivity to simulation error. 1) 24

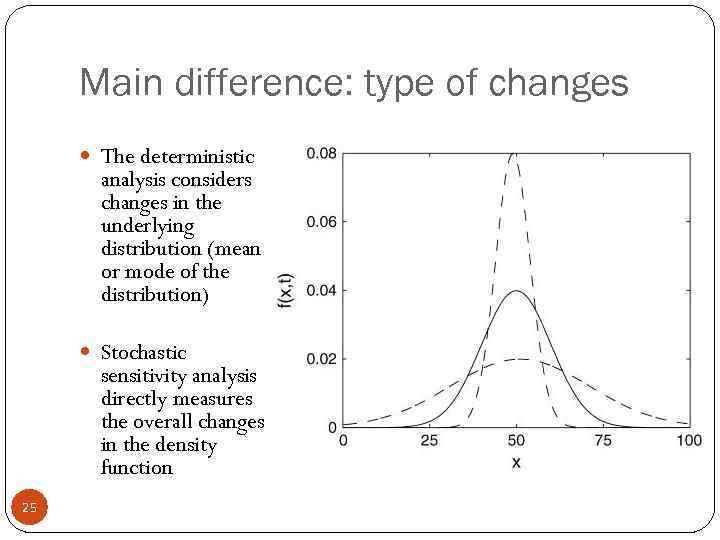
Main difference: type of changes The deterministic analysis considers changes in the underlying distribution (mean or mode of the distribution) Stochastic sensitivity analysis directly measures the overall changes in the density function 25

26

Agenda 1) Introduction 2) Discrete Stochastic Sensitivity Measures 3) Sensitivity Analyses of CMEs 4) Example (Schlögl Model) 5) Conclusion 27

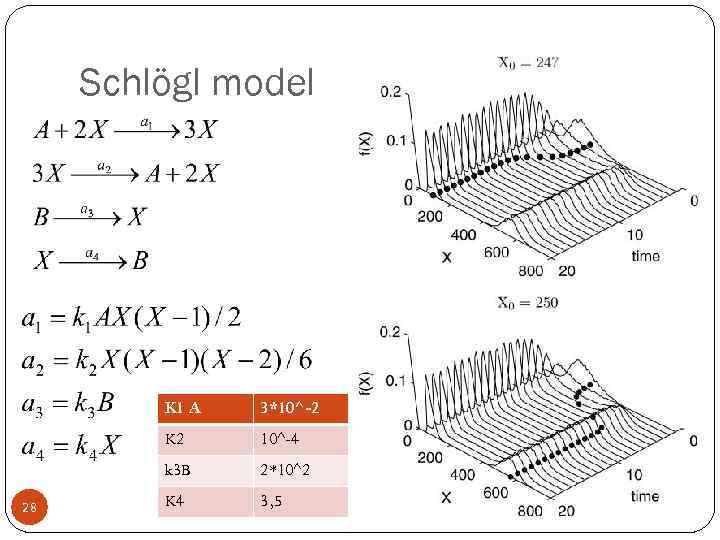
Schlögl model K 1 A K 2 10^-4 k 3 B 28 3*10^-2 2*10^2 K 4 3, 5

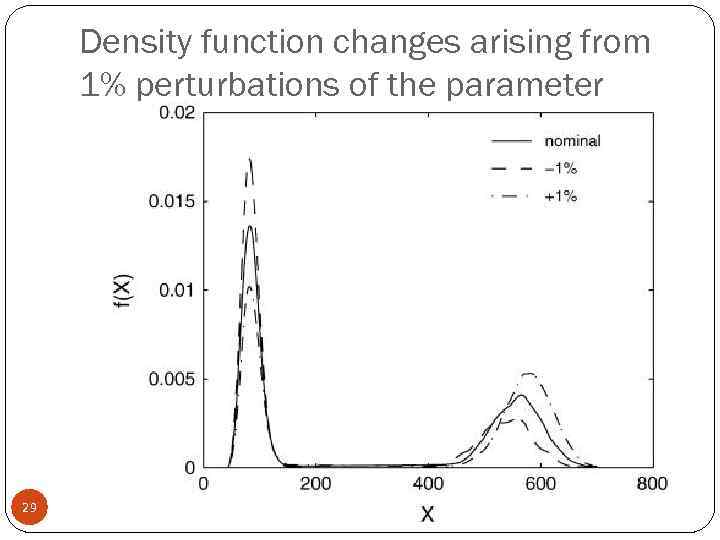
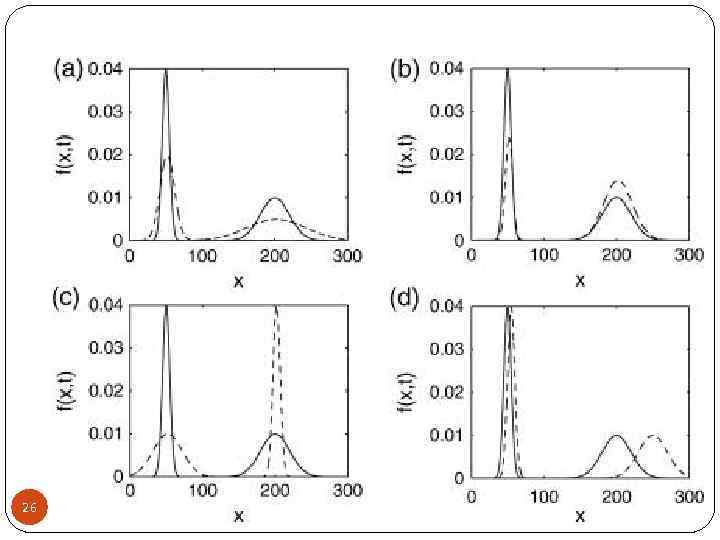
Density function changes arising from 1% perturbations of the parameter 29

30

31

Agenda 1) Introduction 2) Discrete Stochastic Sensitivity Measures 3) Sensitivity Analyses of CMEs 4) Example (Schlögl Model) 5) Conclusion 32

Conclusion Deterministic model lacks information of the true dynamics Sensitivity analysis for discrete stochastic processes developed based on density function sensitivity, using an analog of the classical sensitivity and the Fisher Information Matrix. The proposed analysis applied to a bistable chemical system. Comparisons between the stochastic and deterministic analyses show the significance of explicit consideration of the probabilistic nature in the sensitivity analysis for this class of processes. 33

34