Семинар 4 Минимизация логических функций Метод непосредственного

Семинар 4 Минимизация логических функций

Метод непосредственного упрощения - метод Квайна используется для минимизации логических функций двух-трех переменных. Логическая функция должна быть обязательно задана в канонической форме в виде СДНФ или СКНФ. Минимизация методом Квайна проводится в два этапа в следующей последовательности: 1 шаг – последовательно, начиная с первого члена, сравнивают между собой все члены логической функции: 1 -2, 1 -3, . . . , 2 -3, 2 -4, . . . и т. д. ) на выявление возможности выполнения операции склеивания; склеивающиеся члены подчеркивают , неподчеркнутые члены (если они есть) добавляют в полученное выражения (для СДНФ – при помощи операции ИЛИ, для СКНФ – И); 2 шаг – в полученном по п. 1 выражении проверяют возможность выполнения операции поглощения;

3 шаг – проверяют возможность повторения действий согласно 1 шагу и 2 шагу; этот процесс продолжается до тех пор, пока есть возможности выполнения операций склеивания и поглощения; итоговым результатом этих действий является минимизированная форма записи логической функции. 4 шаг – в виду того, что некоторые члены исходной функции участвовали в операциях склеивания более одного раза, то в итоговом выражении, полученном на 3 шаге, могут появиться избыточные ЭК; для их исключения необходимо построить таблицу реализаций – в столбцах этой таблицы представлены все исходные члены (это КЕ (КН) заданной логической функции), а строки представляют собой ЭК (ЭД) ее минимизированного уравнения; для нахождения минимального покрытия отмечают значком «+» клетки пересечения строк и столбцов, в которых ЭК (ЭД) входят в исходные КЕ (КН), а затем выполняют поиск минимального покрытия, отмечая символом «(+)» , т. е. ЭК (ЭД), которые полностью покрывают исходные КЕ (КН); для столбцов с одним символом «+» строка ЭК (ЭД) является обязательной.

Пример 1 – минимизировать функцию в виде СДНФ. Согласно 1 шагу выполним операции склеивания, т. е. склеиваются следующие члены 1 -2, 1 -3, 2 -4, 3 -4, 4 -5. Не подчеркнутых членов в исходном выражении нет, в итоге получим выражение: В этом выражение согласно 2 шагу операции поглощения должны быть выполнены над 4 и 5 членами, в результате получим выражение: Переходим к 1 шагу и выполняем операции склеивания. Склеивающимися членами являются 1 -4 и 2 -3, их подчеркивают, а не подчеркнутый член 5. В итоге получим выражение: В этом выражении согласно 2 шагу выполним операцию поглощения для 1 и 2 членов, т. е. получим выражение:

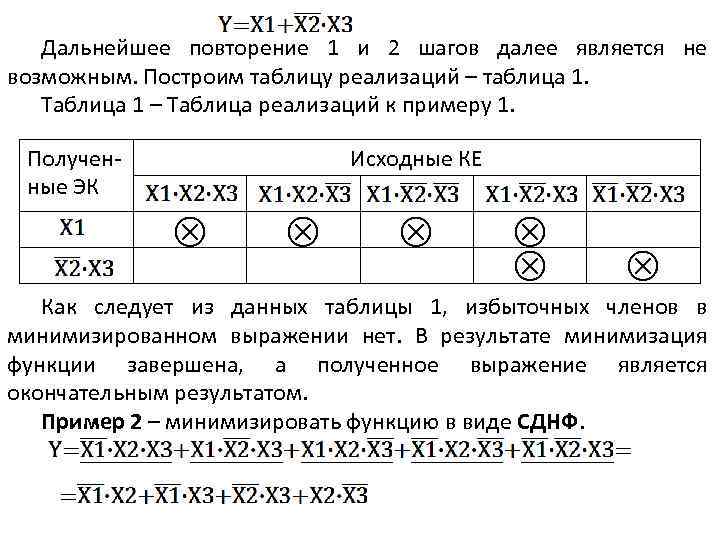Дальнейшее повторение 1 и 2 шагов далее является не возможным. Построим таблицу реализаций – таблица 1. Таблица 1 – Таблица реализаций к примеру 1. Полученные ЭК Исходные КЕ (+) (+) (+) Как следует из данных таблицы 1, избыточных членов в минимизированном выражении нет. В результате минимизация функции завершена, а полученное выражение является окончательным результатом. Пример 2 – минимизировать функцию в виде СДНФ.

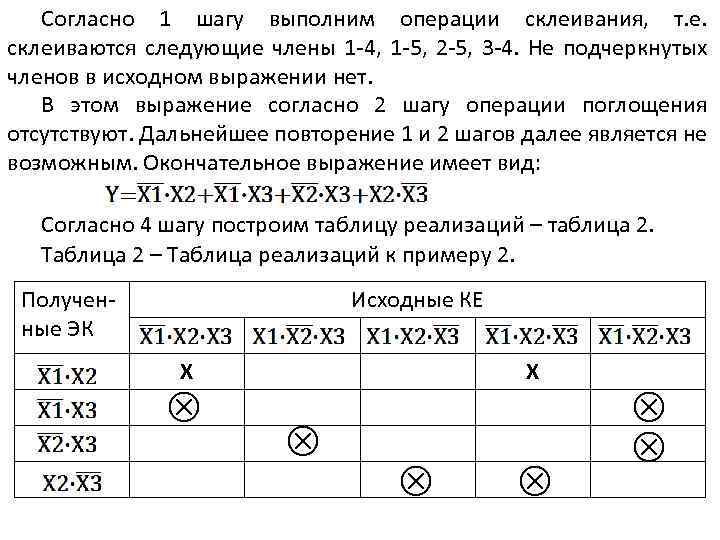Согласно 1 шагу выполним операции склеивания, т. е. склеиваются следующие члены 1 -4, 1 -5, 2 -5, 3 -4. Не подчеркнутых членов в исходном выражении нет. В этом выражение согласно 2 шагу операции поглощения отсутствуют. Дальнейшее повторение 1 и 2 шагов далее является не возможным. Окончательное выражение имеет вид: Согласно 4 шагу построим таблицу реализаций – таблица 2. Таблица 2 – Таблица реализаций к примеру 2. Полученные ЭК Исходные КЕ Х + + +

Как следует из данных таблицы 2, избыточным членом в минимизированном выражении является либо 1, либо 2 ЭК; исключим 1 ЭК – . В результате минимизация функции завершена, окончательное выражение минимизированной функции имеет вид: Метод Квайна –Мак-Класски. Этот метод применяется для логических функций, имеющих от четырех до десяти входных сигналов и один выходной сигнал. Его основой является числовой способ задания функции, которая выражена в СДНФ (допускается задание в виде СКНФ). Пример 3. Рассмотрим этот метод минимизации на примере функции, имеющей запись в СДНФ (таблица истинности отсутствует): Y(X 1, X 2, X 3, X 4)=∑(0, 1, 2, 5, 6, 7, 9, 10, 14) Этап 1. Составляется вспомогательная таблица. Ее число столбцов равно четырем – таблица 3, а число строк зависит от количества КЕ в исходной функции плюс одна строка, т. е. - 10.

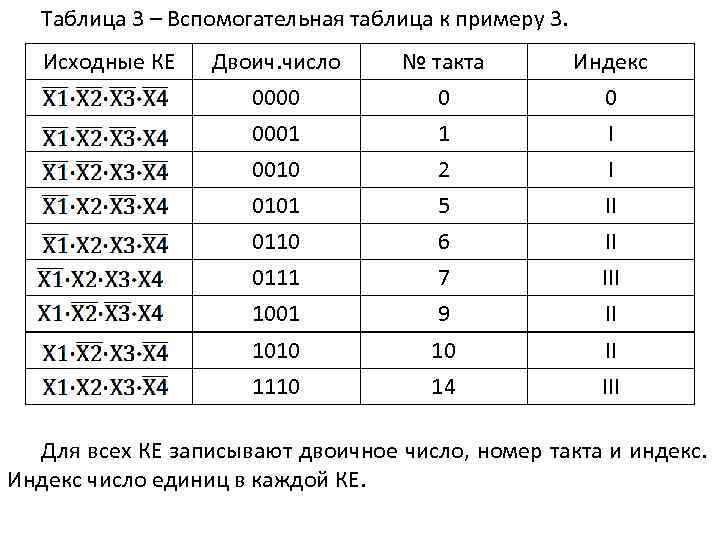Таблица 3 – Вспомогательная таблица к примеру 3. Исходные КЕ Двоич. число 0000 0001 0010 № такта 0 1 2 Индекс 0 I I 0101 0110 5 6 II II 0111 1001 7 9 III II 1010 1110 10 14 II III Для всех КЕ записывают двоичное число, номер такта и индекс. Индекс число единиц в каждой КЕ.

Этап 2. Выполняют группировку КЕ функции. Номер группы равен индексу, все группы располагают в порядке возрастания. В каждой из групп располагают все исходные КЕ в порядке возрастания в виде их цифровых эквивалентов (№ тактов). Получим четыре группы – 0, I, III: 0 0 I 1 2 II 5 6 9 10 III 7 14 Между собой все группы разделяют чертой. Этап 3. Поэтапно проводят операции склеивания.

На каждом этапе склеивания рассматривают КЕ только в соседних группах, индексы которых отличаются только на 1 (т. е. 0 -I, I-II, II-III и т. д. ). В склеивании участвуют только те члены, разница между номерами тактов которых кратна (например: 1, 2, 4, 8 и т. д. ). Склеивание проводят последовательно для каждого члена из группы с меньшим индексом со всеми склеивающимися членами группы с большим индексом. Склеивание осуществляется если номер члена в группе с меньшим индексом меньше номера члена в группе с большим индексом. Например, склеиваются члены: в группах 0+I: 0 и 1, 0 и 2; в группах I+II: 1 и 5, 1 и 9, 2 и 6, 2 и 10 ; в группах. II+III: 5 и 7, 6 и 8, 10 14; члены 9 и 7 в склеивании не участвуют. Члены, участвовавшие в склеивании, помечают символом - *. Члены, не отмеченные *, обозначают различными буквами и выписывают отдельно, они в дальнейших операциях не участвуют и будут учтены на заключительном этапе минимизации.

Запись результатов склеивания – аналогичная записи на этапе 2, только в скобках отмечают выпавшие веса, т. е. числа, кратные . Для рассматриваемого примера получим: 0 0 * 0+I 0, 1 (1) I 1 * 0, 2 (2) 2 * I+II 1, 5 (4) II 5 * 1, 9 (8) 6 * 2, 6 (4) 9 * 2, 10 (8) 10 * II+III 5, 7 (2) III 7 * 6, 7 (1) 14 * 6, 14 (8) 10, 14(4) Этап 4. В полученном выражении (этап 3) если возможно выполняют операции поглощения. В рассматриваемом примере членов, не отмеченных символом *, нет; операции, соответствующие этапу 4, отсутствуют.

Этап 5. Аналогично этапам 3 и 5 повторяют выполнение операций склеивания и поглощения. Этот процесс проходит до тех пор, пока не останутся только одни минимальные члены. Для рассматриваемого примера получим: 0+I I+II II+III 0, 1 (1) 0, 2 (2) 1, 5 (4) 1, 9 (8) 2, 6 (4) * 2, 10 (8)* 5, 7 (2) 6, 7 (1) 6, 14 (8)* 10, 14(4)* I+II+III 2, 6, 10, 14 (4, 8) 2, 10, 6, 14 (8, 4) а=0, 1 (1); б=0, 2 (2); в=1, 5 (4); г=1, 9 (8); д=5, 7 (2); е=6, 7 (1); ж=2, 6, 10, 14 (4, 8)

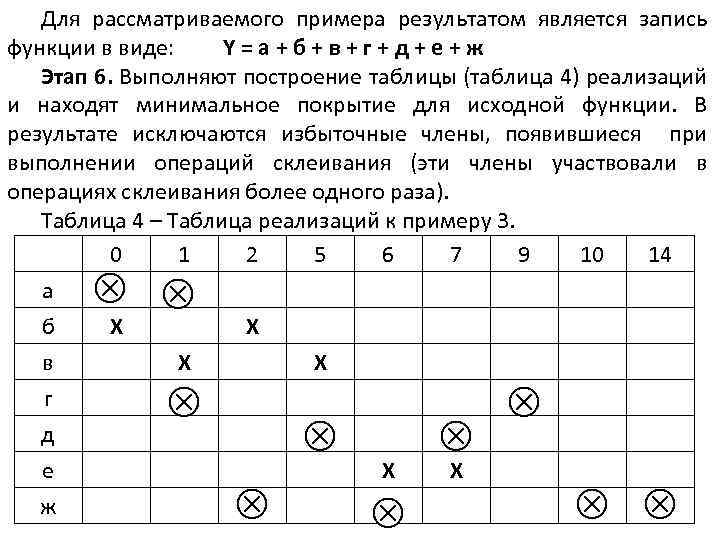Для рассматриваемого примера результатом является запись функции в виде: Y=а+б+в+г+д+е+ж Этап 6. Выполняют построение таблицы (таблица 4) реализаций и находят минимальное покрытие для исходной функции. В результате исключаются избыточные члены, появившиеся при выполнении операций склеивания (эти члены участвовали в операциях склеивания более одного раза). Таблица 4 – Таблица реализаций к примеру 3. 0 1 2 5 6 7 9 10 14 а б Х Х в Х Х г д е ж Х Х

Этап 7. На основе этапа 6 записывают выражение минимизированной логической функции. Для данного примера получим: Y = а + г + д + ж = 0, 1 (1) + 1, 9 (8) + 5, 7 (2) + 2, 6, 10, 14 (4, 8) Проведя подстановку вместо цифровых эквивалентов соответствующих им переменных получим окончательный результат: На этом формализованная минимизация логической функции методом Квайна-Мак-Класски является законченной. При построении схемы на релейно-контактных элементах следует выполнить не формализованный шаг – вынос за скобки одинаковых переменных. В результате получим:

Пример 4. Для мостиковой схемы, приведенной на рис. 1, найти алгоритм работы, выполнить его минимизацию и составить релейно -контактную схему без использования мостиковой структуры. Рис. 1. Схема к примеру 4. Составим таблицу истинности для исходной схемы. Она имеет 32 набора комбинаций входных сигналов – таблица 5. Значения выходного сигнала Y определены согласно схеме – рис. 1. Таблица истинности дополнена столбцом, определяющим номер группы – это индекс. Поскольку количество входных сигналов равно 5 (К 1, К 2, К 3, К 4, К 5), то минимизацию выполним методом Квайна –Мак-Класски.

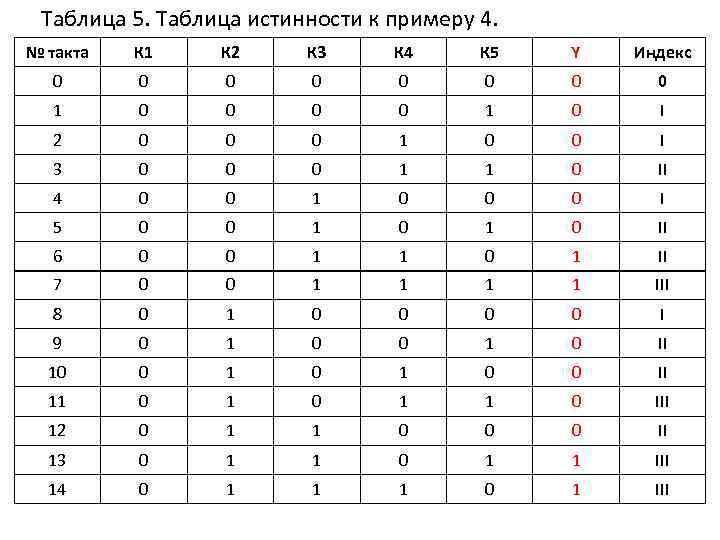Таблица 5. Таблица истинности к примеру 4. № такта К 1 К 2 К 3 0 0 1 0 0 2 0 3 К 4 К 5 Y Индекс 0 0 0 1 0 I 0 0 1 0 0 I 0 0 0 1 1 0 II 4 0 0 1 0 0 0 I 5 0 0 1 0 II 6 0 0 1 1 0 1 II 7 0 0 1 1 III 8 0 1 0 0 I 9 0 1 0 II 10 0 1 0 0 II 11 0 1 1 0 III 12 0 1 1 0 0 0 II 13 0 1 1 III 14 0 1 1 1 0 1 III

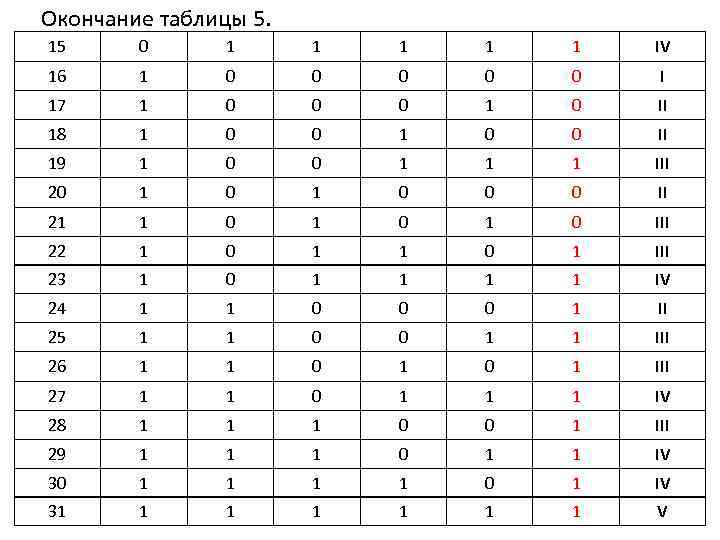Окончание таблицы 5. 15 0 1 1 1 IV 16 1 0 0 0 I 17 1 0 0 0 1 0 II 18 1 0 0 II 19 1 0 0 1 1 1 III 20 1 0 0 0 II 21 1 0 1 0 III 22 1 0 1 III 23 1 0 1 1 IV 24 1 1 0 0 0 1 II 25 1 1 0 0 1 1 III 26 1 1 0 1 III 27 1 1 0 1 1 1 IV 28 1 1 1 0 0 1 III 29 1 1 1 0 1 1 IV 30 1 1 0 1 IV 31 1 1 1 V

Согласно данным таблицы 5 запишем алгоритм управления в виде цифровых эквивалентов: Y(К 1, К 2, К 3, К 4, К 5)= ∑(6, 7, 13, 14, 15, 19, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31) Члены, участвующие в минимизации, находятся в группах: II, IV, V. Минимизация проведена аналогично примеру 3. Этапы 2 и 3. II 6 * 24* III 7 * 13* 14* 19* 22* 25* 26* 28* IV V 15* 23* 27* 29* 30* 31*

II+III IV+V 6, 7 (1) * 6, 14 (8) * 6, 22 (16)* 24, 25 (1) * 24, 26 (2) * 24, 28 (4) * 15, 31 (16)* 23, 31 (8)* 27, 31 (4)* 29, 31 (2)* 30, 31 (1)* Этапы 4 и 5. III+IV 7, 15 (8)* 7, 23 (16)* 13, 15 (2)* 13, 29 (16)* 14, 15 (1)* 14, 30 (30)* 19, 23 (4)* 19, 27 (8)* 22, 23 (1)* 22, 30 (8)* 25, 27 (2)* 25, 29 (4)* 26, 27 (1)* 26, 30 (4)* 28, 29 (1)* 28, 30 (2)*

II+III+IV 6, 7, 14, 15 (1, 8) 6, 7, 22, 23 (1, 16) 6, 14, 7, 15 (8, 1) 6, 14, 22, 30 (8, 16) 6, 22, 7, 23 (16, 1) 6, 22, 14, 30 (16, 8) 24, 25, 26, 27(1, 2) 24, 25, 28, 29(1, 4) 24, 26, 25, 27(2, 1) 24, 26, 28, 30(2, 4) 24, 28, 25, 29(4, 1) 24, 28, 26, 30(4, 2) 6, 7, 14, 15 (1, 8) * 6, 7, 22, 23 (1, 16) * 6, 14, 22, 30 (8, 16) * 24, 25, 26, 27(1, 2) * 24, 25, 28, 29(1, 4) * 24, 26, 28, 30(2, 4) * выполнив поглощения получим

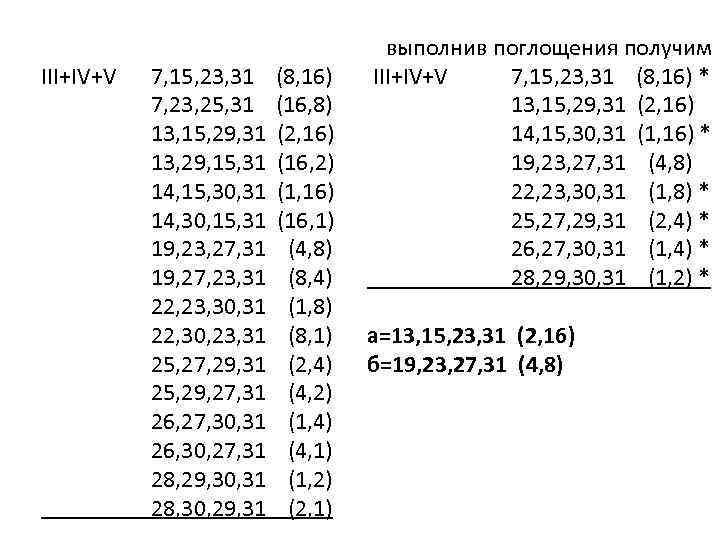III+IV+V 7, 15, 23, 31 (8, 16) 7, 23, 25, 31 (16, 8) 13, 15, 29, 31 (2, 16) 13, 29, 15, 31 (16, 2) 14, 15, 30, 31 (1, 16) 14, 30, 15, 31 (16, 1) 19, 23, 27, 31 (4, 8) 19, 27, 23, 31 (8, 4) 22, 23, 30, 31 (1, 8) 22, 30, 23, 31 (8, 1) 25, 27, 29, 31 (2, 4) 25, 29, 27, 31 (4, 2) 26, 27, 30, 31 (1, 4) 26, 30, 27, 31 (4, 1) 28, 29, 30, 31 (1, 2) 28, 30, 29, 31 (2, 1) выполнив поглощения получим III+IV+V 7, 15, 23, 31 (8, 16) * 13, 15, 29, 31 (2, 16) 14, 15, 30, 31 (1, 16) * 19, 23, 27, 31 (4, 8) 22, 23, 30, 31 (1, 8) * 25, 27, 29, 31 (2, 4) * 26, 27, 30, 31 (1, 4) * 28, 29, 30, 31 (1, 2) * а=13, 15, 23, 31 (2, 16) б=19, 23, 27, 31 (4, 8)

II+IV+V 6, 7, 14, 15, 22, 23, 30, 31 (1, 8, 16) 6, 7, 22, 23, 14, 15, 30, 31 (1, 16, 8) 6, 14, 22, 30, 7, 15, 23, 31 (8, 16, 1) 24, 25, 26, 27, 28, 29, 30, 31 (1, 2, 4) 24, 25, 28, 29, 26, 27, 30, 31 (1, 4, 2) 24, 26, 28, 30, 25, 27, 29, 31 (2, 4, 1) выполнив поглощения получим II+IV+V 6, 7, 14, 15, 22, 23, 30, 31 (1, 8, 16) 24, 25, 26, 27, 28, 29, 30, 31 (1, 2, 4) В последнем выражении остались только минимальные члены, т. е. : в= 6, 7, 14, 15, 22, 23, 30, 31 (1, 8, 16) г= 24, 25, 26, 27, 28, 29, 30, 31 (1, 2, 4). Для рассматриваемого примера результатом является запись функции в виде: Y=а+б+в+г

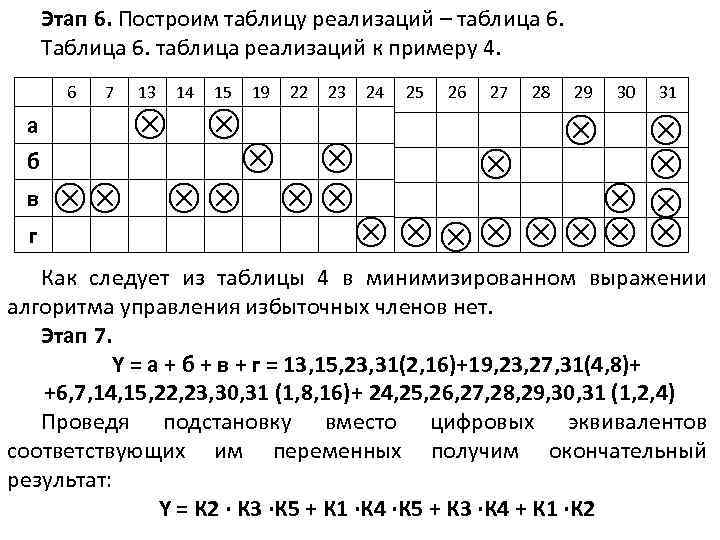Этап 6. Построим таблицу реализаций – таблица 6. Таблица 6. таблица реализаций к примеру 4. 6 7 13 14 15 19 22 23 24 25 26 27 28 29 30 31 а б в г Как следует из таблицы 4 в минимизированном выражении алгоритма управления избыточных членов нет. Этап 7. Y = а + б + в + г = 13, 15, 23, 31(2, 16)+19, 23, 27, 31(4, 8)+ +6, 7, 14, 15, 22, 23, 30, 31 (1, 8, 16)+ 24, 25, 26, 27, 28, 29, 30, 31 (1, 2, 4) Проведя подстановку вместо цифровых эквивалентов соответствующих им переменных получим окончательный результат: Y = К 2 ∙ К 3 ∙К 5 + К 1 ∙К 4 ∙К 5 + К 3 ∙К 4 + К 1 ∙К 2

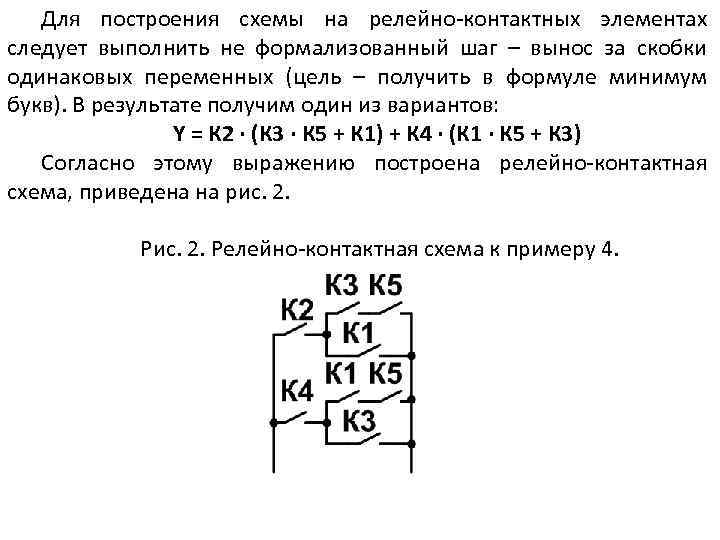Для построения схемы на релейно-контактных элементах следует выполнить не формализованный шаг – вынос за скобки одинаковых переменных (цель – получить в формуле минимум букв). В результате получим один из вариантов: Y = К 2 ∙ (К 3 ∙ К 5 + К 1) + К 4 ∙ (К 1 ∙ К 5 + К 3) Согласно этому выражению построена релейно-контактная схема, приведена на рис. 2. Релейно-контактная схема к примеру 4.