Self Weight Consolidation of Soft Sediments Some Implications

Self Weight Consolidation of Soft Sediments: Some Implications for Climate Studies N. Keith Tovey 1 , Mike Paul 2, Yap Chui-Wah 3, and Simon Tovey 4 University of West Indies, Trinidad 9 th January 2003 1 School of Environmental Sciences, University of East Anglia, Norwich, NR 4 7 TJ, UK 2 School of Life Sciences, Heriot Watt University, Edinburgh, EH 14 4 AS, UK 3 Singapore Meteorological Service, Changi Airport, Singapore 918141 4 101 Media Ltd, Keswick Hall, NR 4 6 TJ, Norwich, UK Acknowledgements: • Geotechnical Engineering Office, Hong Kong • Civil Engineering Office, Hong Kong • Prof. Muneki Mitamura, Osaka • Carolyn Sharp, University of East Anglia • British Council

The Problem • What effect does self-weight consolidation (auto-compaction) have on our understanding of Marine Sequences? • What processes are involved? • What are the magnitudes of such effects? • How easy is it to correct for these effects?

Holocene Marine Deposits: modelling self-weight consolidation 1. Background to self-weight consolidation issues 2. Site Locations 3. Equilibrium Self-Weight Compaction 4. Existence of Omega Point? 5. True Sedimentation Rates 6. Modelling pore-pressure dissipation 7. Conclusions 8. Postscript for ENV-2 E 1 Y

Why are such studies of relevance? Interpretation of sequences is often done on a linear length basis. i. e. two points in a sequence may be dated and a sedimentation rate estimated from dates and distances between the two points. This does not allow for self-weight consolidation - strictly it should be done using a linear mass interpolation - rarely is the case. This is of particular importance in unravelling Holocene sequences where the apparent deposition rate is of the order of 0. 5 - 5 mm per year. It is of significance in dating studies, estimation of palaeo-water depths in tidal modelling, salt marsh studies, archeology etc.

Holocene Marine Deposits: modelling self-weight consolidation 1. Background to self-weight consolidation issues 2. Site Locations 3. Equilibrium Self-Weight Compaction 4. Existence of Omega Point? 5. True Sedimentation Rates 6. Modelling pore-pressure dissipation 7. Conclusions 8. Postscript for ENV-2 E 1 Y

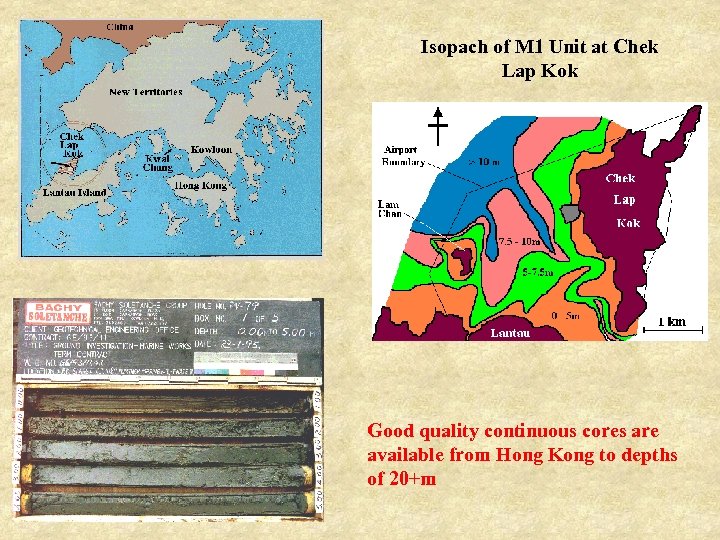Isopach of M 1 Unit at Chek Lap Kok Good quality continuous cores are available from Hong Kong to depths of 20+m

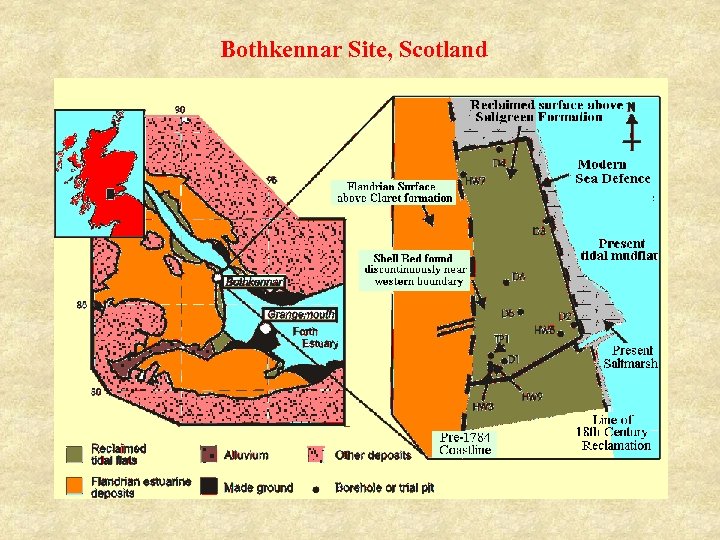Bothkennar Site, Scotland

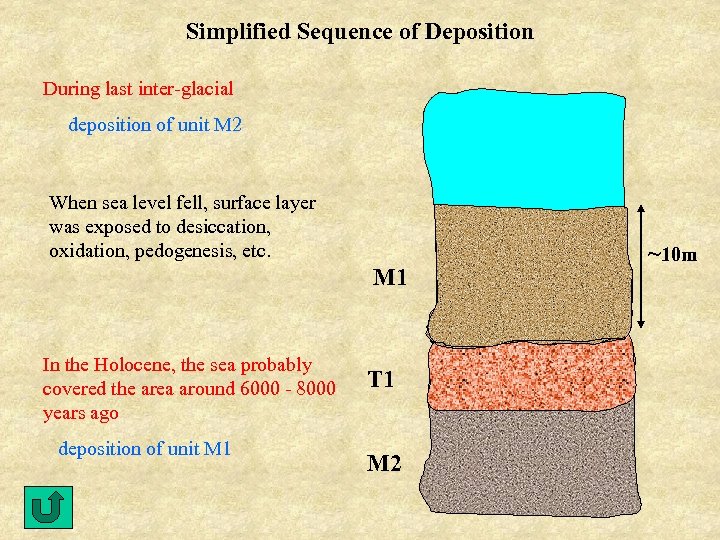Simplified Sequence of Deposition During last inter-glacial deposition of unit M 2 When sea level fell, surface layer was exposed to desiccation, oxidation, pedogenesis, etc. M 1 In the Holocene, the sea probably covered the area around 6000 - 8000 years ago deposition of unit M 1 T 1 M 2 ~10 m

From core record, several different sequences have been identified Classification after Yim Present work models Holocene sequence

Holocene Marine Deposits: modelling self-weight consolidation 1. Background to self-weight consolidation issues 2. Site Locations 3. Equilibrium Self-Weight Compaction 4. Existence of Omega Point? 5. True Sedimentation Rates 6. Modelling pore-pressure dissipation 7. Conclusions 8. Postscript for ENV-2 E 1 Y

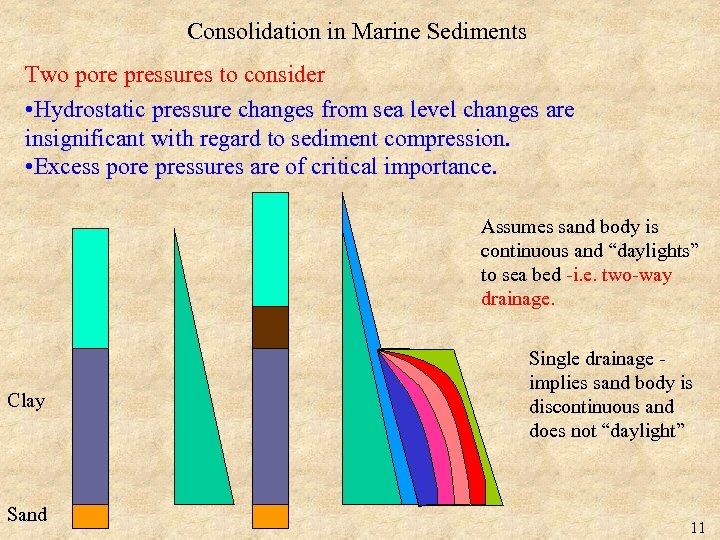Consolidation in Marine Sediments Two pore pressures to consider • Hydrostatic pressure changes from sea level changes are insignificant with regard to sediment compression. • Excess pore pressures are of critical importance. Assumes sand body is continuous and “daylights” to sea bed -i. e. two-way drainage. Clay Sand Single drainage implies sand body is discontinuous and does not “daylight” 11

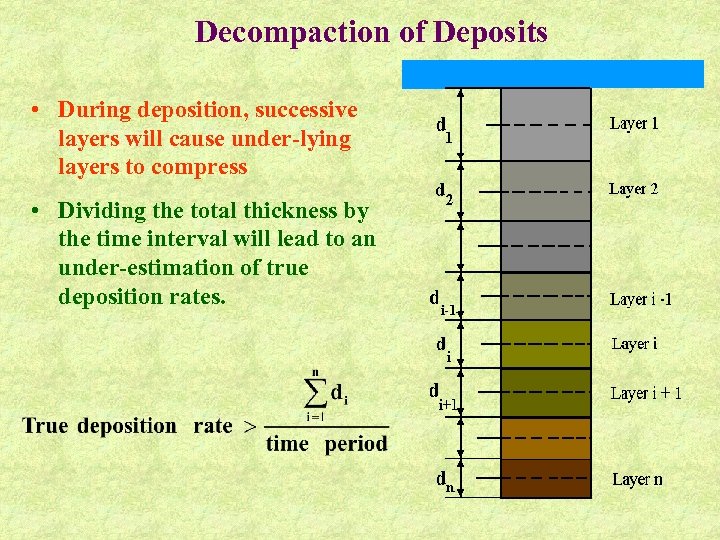Decompaction of Deposits • During deposition, successive layers will cause under-lying layers to compress • Dividing the total thickness by the time interval will lead to an under-estimation of true deposition rates.

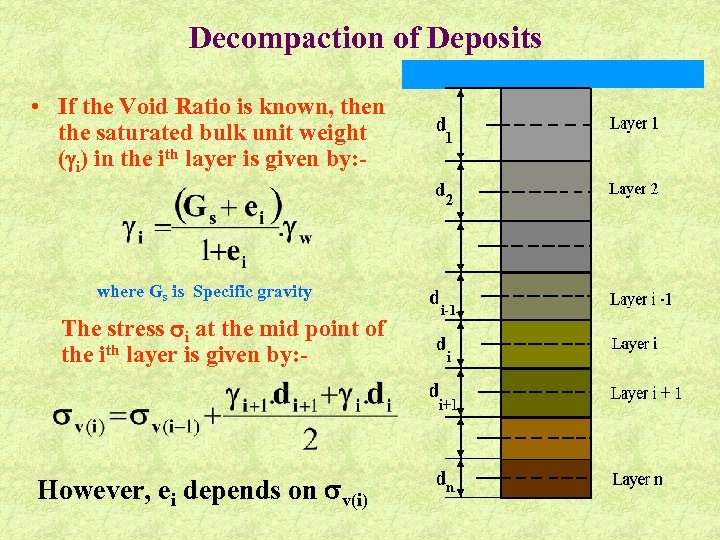Decompaction of Deposits • If the Void Ratio is known, then the saturated bulk unit weight ( i) in the ith layer is given by: - where Gs is Specific gravity The stress i at the mid point of the ith layer is given by: - However, ei depends on v(i)

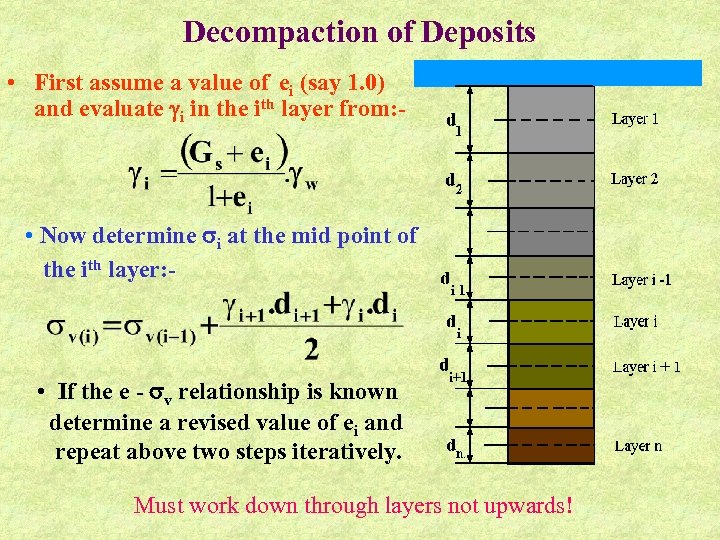Decompaction of Deposits • First assume a value of ei (say 1. 0) and evaluate i in the ith layer from: - • Now determine i at the mid point of the ith layer: - • If the e - v relationship is known determine a revised value of ei and repeat above two steps iteratively. Must work down through layers not upwards!

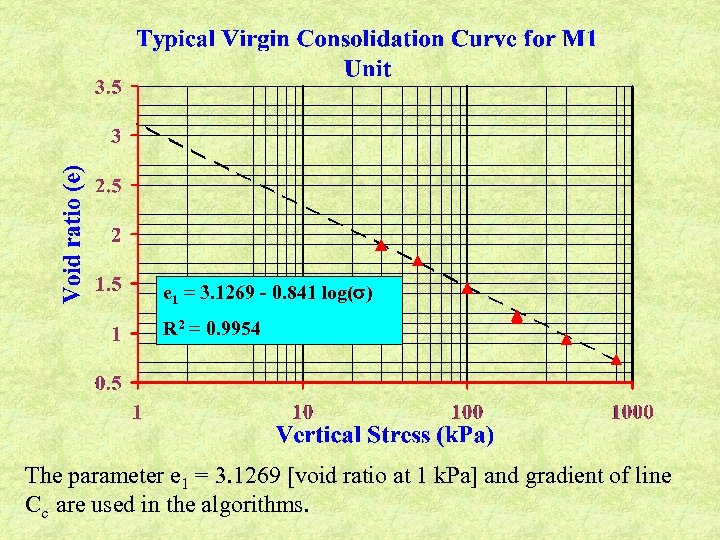e 1 = 3. 1269 - 0. 841 log( ) R 2 = 0. 9954 The parameter e 1 = 3. 1269 [void ratio at 1 k. Pa] and gradient of line Cc are used in the algorithms.

Holocene Marine Deposits: modelling self-weight consolidation 1. Background to self-weight consolidation issues 2. Site Locations 3. Equilibrium Self-Weight Compaction 4. Existence of Omega Point? 5. True Sedimentation Rates 6. Modelling pore-pressure dissipation 7. Conclusions 8. Postscript for ENV-2 E 1 Y 17

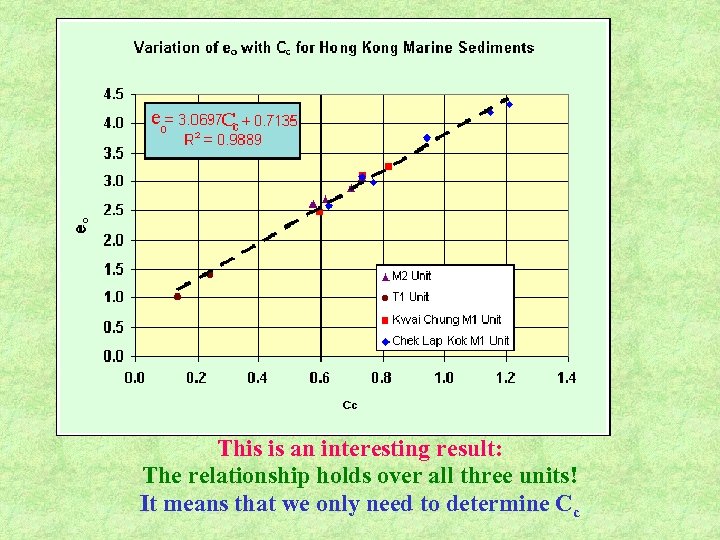This is an interesting result: The relationship holds over all three units! It means that we only need to determine Cc

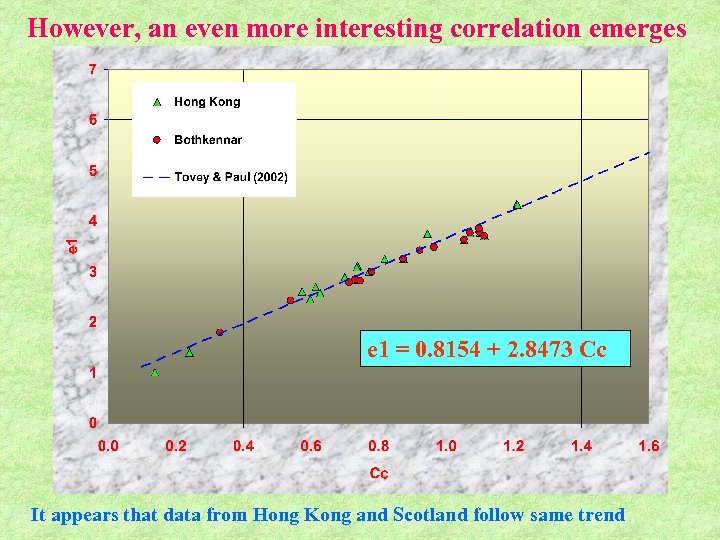However, an even more interesting correlation emerges e 1 = 0. 8154 + 2. 8473 Cc It appears that data from Hong Kong and Scotland follow same trend

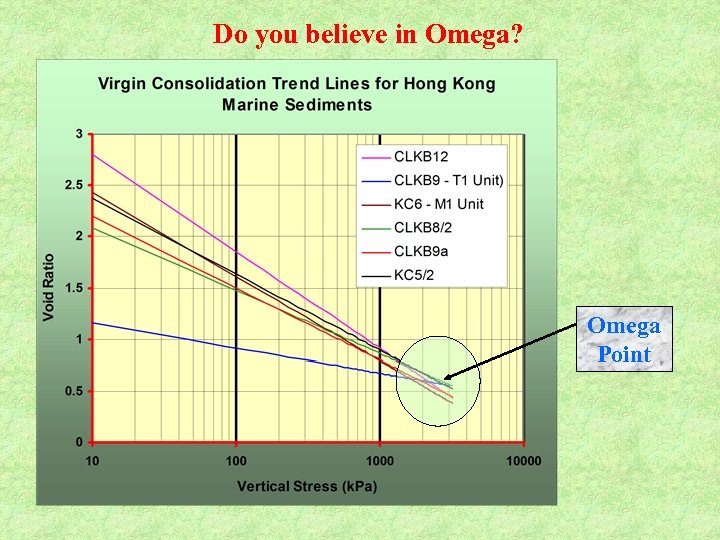Do you believe in Omega? Omega Point

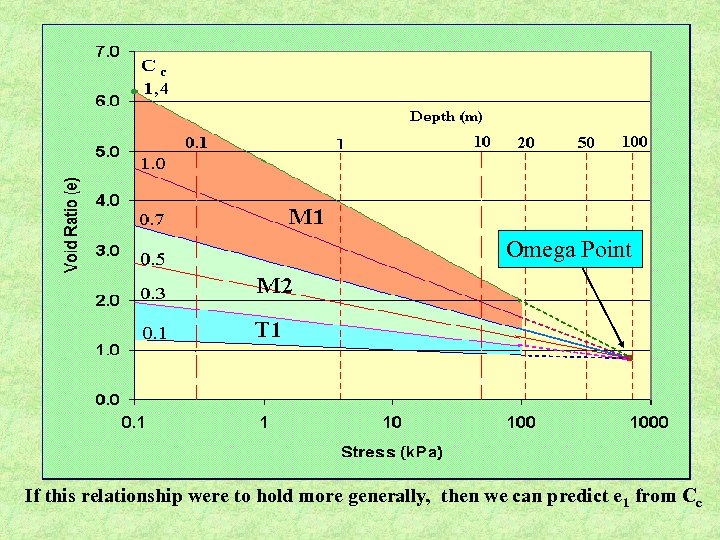Omega Point If this relationship were to hold more generally, then we can predict e 1 from Cc

Inclusion of many more data points still confirms a relationship e 1 = 0. 8662 + 2. 7111 Cc R 2 = 0. 9775 T 1 M 2 M 1 Gassy sediments

Holocene Marine Deposits: modelling self-weight consolidation 1. Background to self-weight consolidation issues 2. Site Locations 3. Equilibrium Self-Weight Compaction 4. Existence of Omega Point? 5. True Sedimentation Rates 6. Modelling pore-pressure dissipation 7. Conclusions 8. Postscript for ENV-2 E 1 Y 23

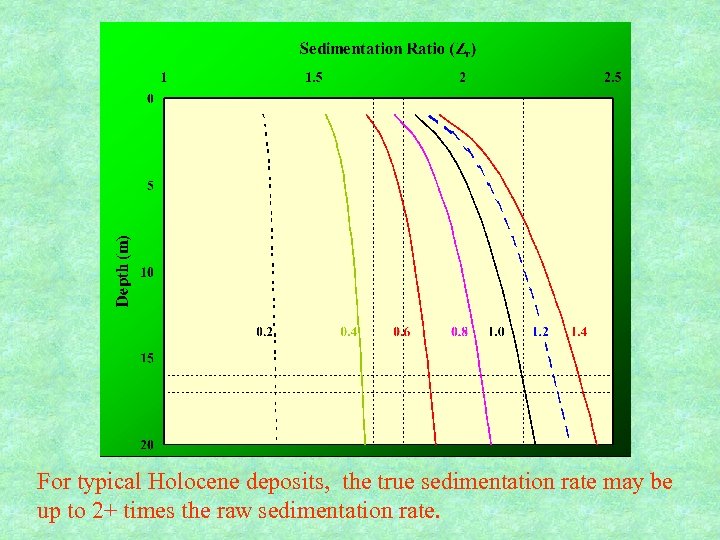For typical Holocene deposits, the true sedimentation rate may be up to 2+ times the raw sedimentation rate.

What is a typical value for sedimentation rate? • Assume 10 m Holocene sequence and Cc approximately 1. 0. • If sea level rose about 6500 years ago, then raw sedimentation rate is about 1. 5 mm per year • But after correction, the true rate for the Hong Kong M 1 unit is > 3 mm per year. • Any modelling must use layers no thicker than this.

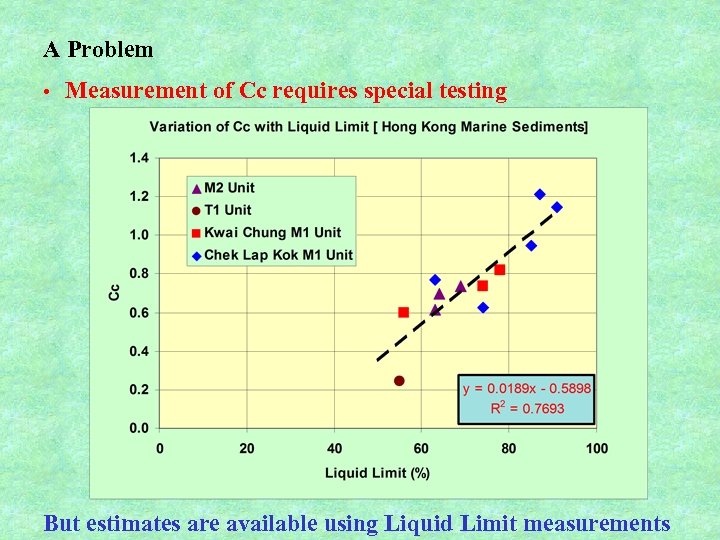A Problem • Measurement of Cc requires special testing But estimates are available using Liquid Limit measurements

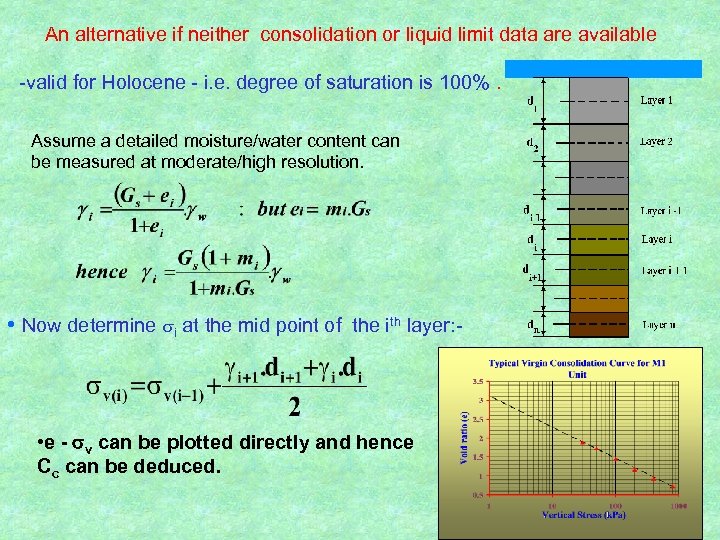An alternative if neither consolidation or liquid limit data are available -valid for Holocene - i. e. degree of saturation is 100%. Assume a detailed moisture/water content can be measured at moderate/high resolution. • Now determine i at the mid point of the ith layer: - • e - v can be plotted directly and hence Cc can be deduced.

Porosity varies significantly in uppermost 2 m. Void ratio of 2 is equivalent to a porosity of 0. 667 Void ratio of 4 is equivalent to a porosity of 0. 8

The values of moisture content are almost always above the mean prediction suggesting a more open structure than expected

Holocene Marine Deposits: modelling self-weight consolidation 1. Background to self-weight consolidation issues 2. Site Locations 3. Equilibrium Self-Weight Compaction 4. Existence of Omega Point? 5. True Sedimentation Rates 6. Modelling pore-pressure dissipation 7. Conclusions 8. Postscript for ENV-2 E 1 Y 30

• Equilibrium self-weight consolidation analysis assumes that after each increment all excess pore pressure is dissipated. • Conventional wisdom suggests that with all normal sedimentation rates, dissipation will be complete within an annual deposition cycle. • This is true provided drainage paths are NOT long. • However, will this be true for deep sequences where drainage paths are long?

The governing equation for dissipation of pore pressure (u) by: - where cv is the coefficient of consolidation and may be found from: where k is permeability and mv is determined from Cc To proceed we need a relationship to determine k

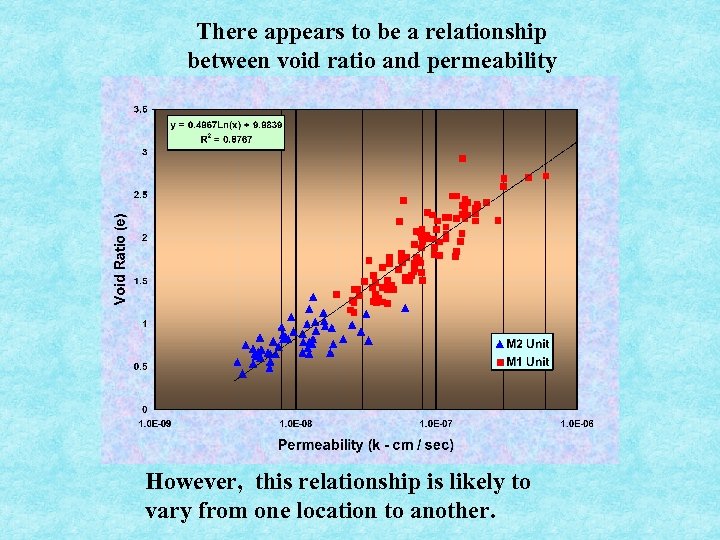There appears to be a relationship between void ratio and permeability However, this relationship is likely to vary from one location to another.

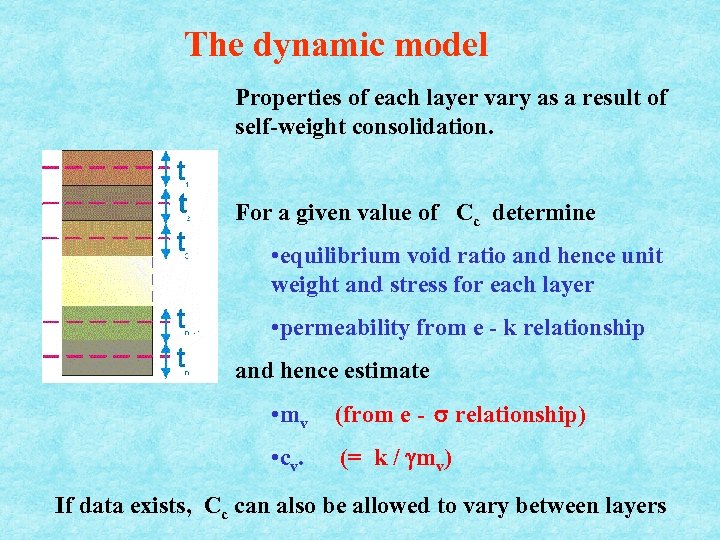The dynamic model Properties of each layer vary as a result of self-weight consolidation. For a given value of Cc determine • equilibrium void ratio and hence unit weight and stress for each layer • permeability from e - k relationship and hence estimate • mv (from e - relationship) • cv. (= k / mv) If data exists, Cc can also be allowed to vary between layers

Choice of initial layer thickness The void ratio varying rapidly in top 1 - 2 m, and layer thickness must reflect this and also be able to model and annual accumulation. > Layer thicknesses ~ 3 mm should be used. > ~ 3000 layers A Problem: • simple analysis using FTCS method will require time steps < 100 secs for stability very computer intensive. • Crank Nicholson method is stable irrespective of time step, although 100 iterations per year are still needed for spatial precision.

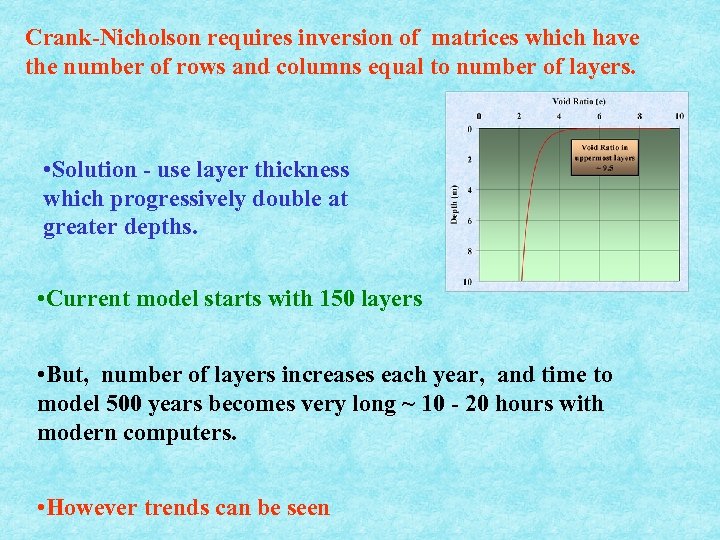Crank-Nicholson requires inversion of matrices which have the number of rows and columns equal to number of layers. • Solution - use layer thickness which progressively double at greater depths. • Current model starts with 150 layers • But, number of layers increases each year, and time to model 500 years becomes very long ~ 10 - 20 hours with modern computers. • However trends can be seen

Results of pore pressure dissipation over first 10 years - annual increment as determined by equilibrium analysis Below 3 m there is no dissipation in year 1. There is evidence of a small amount of dissipation after 10 years.

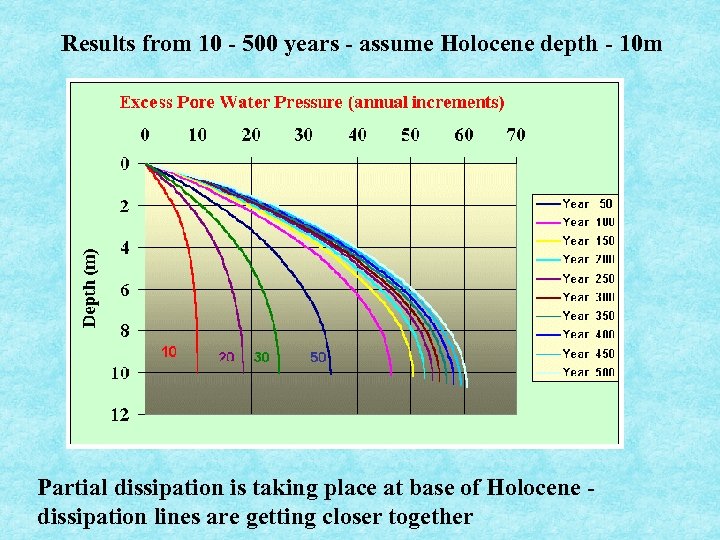Results from 10 - 500 years - assume Holocene depth - 10 m Partial dissipation is taking place at base of Holocene dissipation lines are getting closer together

The presence of excess pore pressures would lead to higher water contents than predicted by steady state analysis Could this be difference be a result of bio-turbation? Unlikely to be the sole cause as deviation increases with depth just as residual pore pressures do.

Recent results from Japan • 18 consolidation tests were done on a single borehole • different values of Cc were measured. • modify steady state analysis to allow for this variation • predicted and actual water are similar at base of Holocene • implies full dissipation of pore pressure > double drainage.

Holocene Marine Deposits: modelling self-weight consolidation 1. Background to self-weight consolidation issues 2. Site Locations 3. Equilibrium Self-Weight Compaction 4. Existence of Omega Point? 5. True Sedimentation Rates 6. Modelling pore-pressure dissipation 7. Conclusions 8. Postscript for ENV-2 E 1 Y 41

Conclusions • raw sedimentation rates significantly underestimate true sedimentation rates by a factor of 2 or more • from consolidation theory, estimates of true porosity and hence sedimentation rates are possible • excess pore pressures arising from annual deposition remain at the end of the year in sequences thicker than about 2 m • pore pressures continue to build up each year > higher than predicted equilibrium moisture contents • the excess moisture content distribution gives an indication of drainage conditions prevailing.

The future • correlation of excess pore water pressures with excess water content - does this explain the full difference between steady state model and actual data points? > need to model over the whole Holocene period • develop model to include pre-Holocene layers > estimates of palaeo-hydrology And finally: The research in this paper is a direct consequence of discussions held at the 2 nd Annual Meeting of IGCP-396 in Durham UK (1997).

Holocene Marine Deposits: modelling self-weight consolidation 1. Background to self-weight consolidation issues 2. Site Locations 3. Equilibrium Self-Weight Compaction 4. Existence of Omega Point? 5. True Sedimentation Rates 6. Modelling pore-pressure dissipation 7. Conclusions 8. Postscript for ENV-2 E 1 Y 44

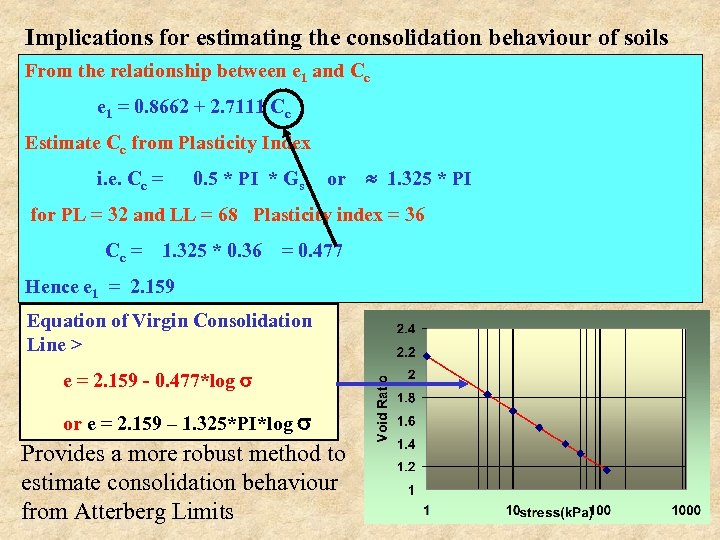Implications for estimating the consolidation behaviour of soils From the relationship between e 1 and Cc e 1 = 0. 8662 + 2. 7111 Cc Estimate Cc from Plasticity Index i. e. Cc = 0. 5 * PI * Gs or 1. 325 * PI for PL = 32 and LL = 68 Plasticity index = 36 Cc = 1. 325 * 0. 36 = 0. 477 Hence e 1 = 2. 159 Equation of Virgin Consolidation Line > e = 2. 159 - 0. 477*log or e = 2. 159 – 1. 325*PI*log Provides a more robust method to estimate consolidation behaviour from Atterberg Limits

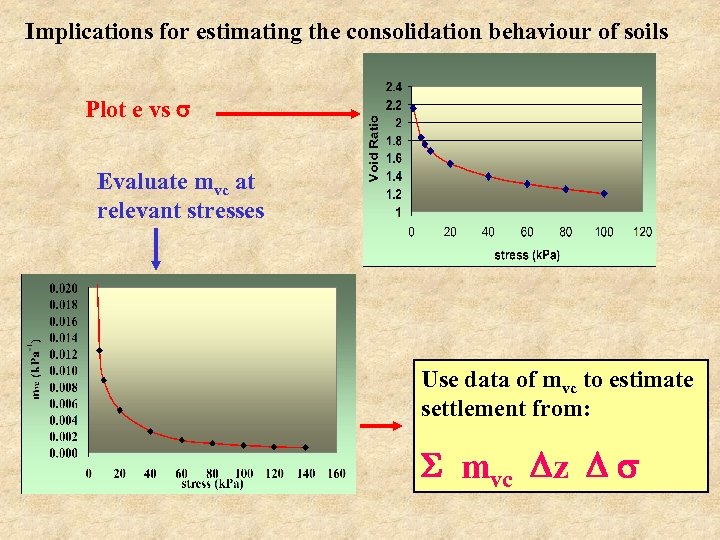Implications for estimating the consolidation behaviour of soils Plot e vs Evaluate mvc at relevant stresses Use data of mvc to estimate settlement from: mvc z