Self-Regulated Learning and Proportional Reasoning Explorations into SRL

Self-Regulated Learning and Proportional Reasoning: Explorations into SRL in the Mathematics Classroom Charles Darr and Jonathan Fisher

Applying Self-Regulated Learning to Mathematics Instruction Self-Regulated Learning is. . . “… a major objective of mathematics education, on the one hand, and … a crucial characteristic of effective mathematics learning on the other” (De Corte et al, 2000).

What is Self Regulated Learning? Theories on self-regulated learning (SRL) describe how students become: “ … masters of their own learning processes” (Zimmerman, 1998). According to Forethought Zimmerman, SRL involves cyclical processes of forethought, performance control and Self-reflection self-reflection Performance control

Becoming a Self-Regulated Learner Observation Emulation Students get there by passing through stages of observation, emulation, selfcontrol and self-regulation. Self Control In Mathematics Education, SRL is particularly relevant to problem solving. Self. Regulation

Self-Regulation and Problem Solving? Expert Problem Solvers Naive Problem Solvers Fully regulated. Haphazard Analyse Use Direct Translation Methods Plan Explore Verify Problem of Inert (nontransferable) Knowledge

Inert Knowledge? Knowledge that is in the student’s mind, but which can not be applied in new situations.

What does SRL Look Like in the Mathematics Classroom? In a review of research into SRL in mathematics, De Corte et al (2000, p. 196), list three components of instruction that appear to foster self-regulation: • realistic and challenging tasks; • variation in teaching methods including teacher modelling, guided practice, small group work and whole class instruction; • classrooms that foster positive dispositions towards learning mathematics.

Our Study Our study explored how components of SRL might be integrated into classroom teaching and learning in the area of proportional reasoning. Taking a lead from Moss and Case (1999) we designed a series of interactive lessons that began with instruction on percentages. We hoped to: Appeal to students intuitive sense of proportionality Motivate them to engage in problem-solving behaviours Develop opportunities for classroom discourse that modelled and supported self-regulation.

What is Proportional Reasoning? According to Piaget it is: …. a capability which ushers in a significant conceptual shift from concrete operational levels of thought to formal operational levels of thought (Piaget & Beth, 1966).

What is Proportional Reasoning? Proportional Reasoning is in essence a process of comparing one relative amount with another (Sophian and Wood, 1997, p. 309). When two quantities vary in such a way that one of them is a constant multiple of the other, the two quantities are proportional (Stanley et al, 2003, p. 2).

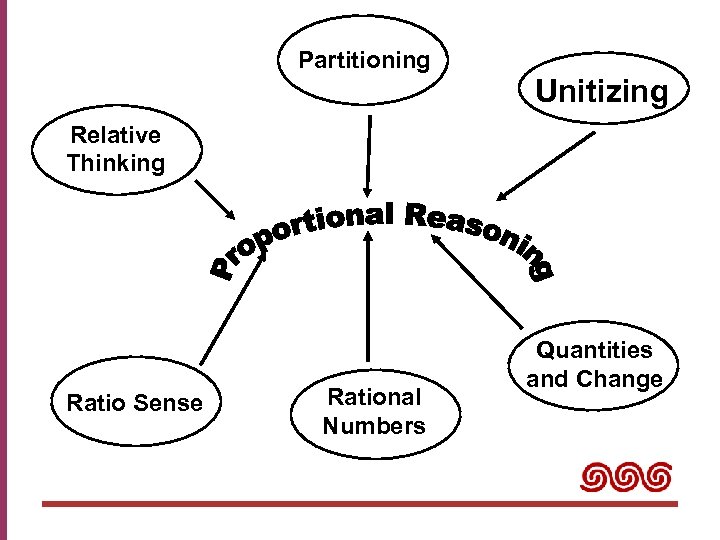Partitioning Unitizing Relative Thinking Ratio Sense Rational Numbers Quantities and Change

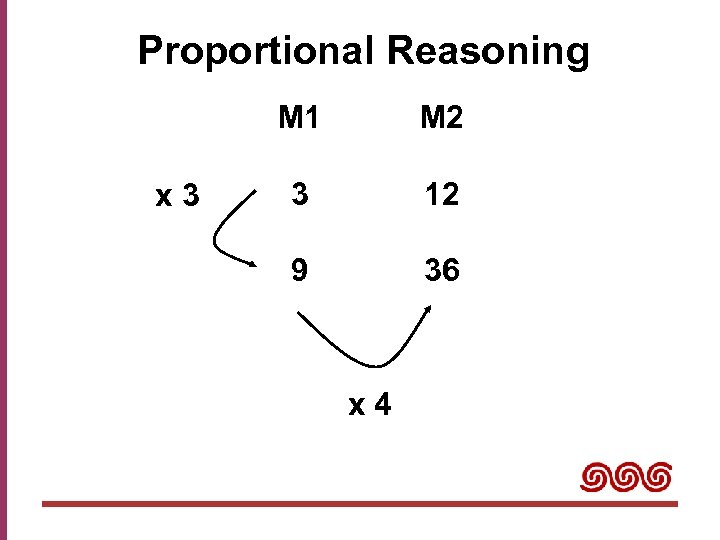Proportional Reasoning M 1 x 3 M 2 3 12 9 36 x 4

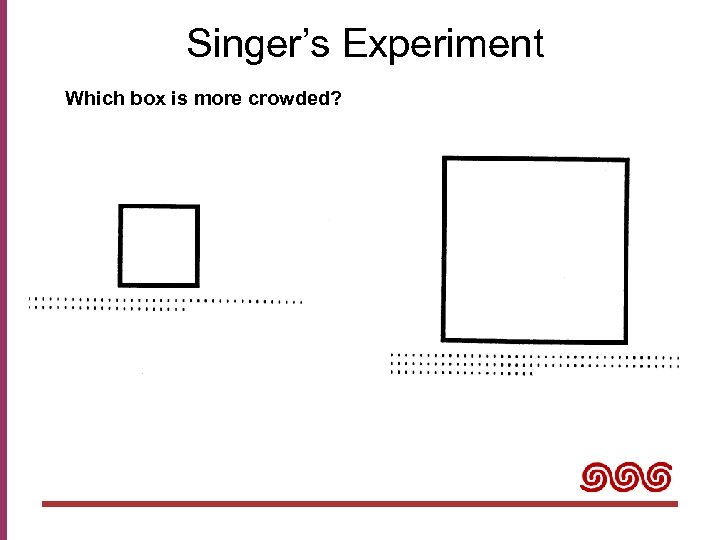Singer’s Experiment Which box is more crowded?

Percentages as a Site for Proportional Reasoning What is 15% of 40? Not long ago $100 in $NZ was worth about $40 in $US. How much would have $15 in $NZ been worth in $US? When my scale is 1: 100 the length is 15. How long will it be when the scale is 1: 40? A stack of 40 books is 100 cm high, how high will a stack of 15 books be? If I can buy 40 ice-blocks for $100, how many can I buy for $15?

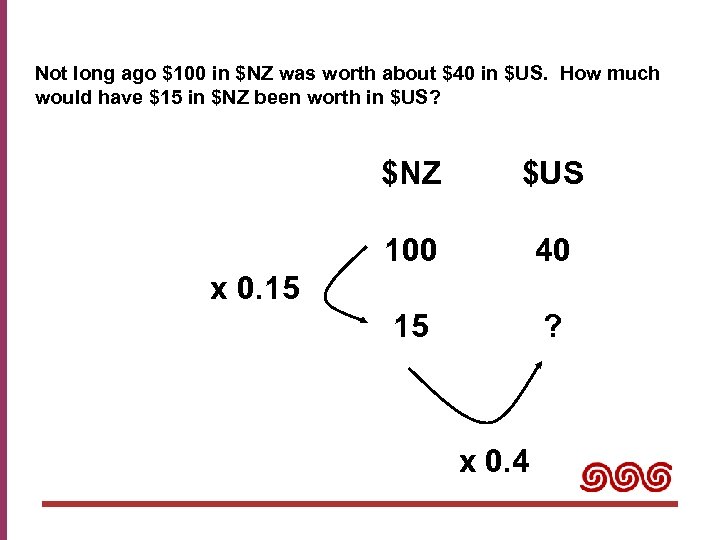Not long ago $100 in $NZ was worth about $40 in $US. How much would have $15 in $NZ been worth in $US? $NZ $US 100 40 15 ? x 0. 15 x 0. 4

Context and Data Sources Context • 12 lessons in a Year 7 class • Mid-decile school • Class of 32 students Data Sources • Pre and post interviews • Pre and post test • Written journal responses • Classroom video

Enhancing SRL We found two elements of Maths instruction that enhanced opportunities for students to practices or observe selfregulating behaviour. These were, the use of: • Rich representations (or models) of problem situations; and. . . • Reflective journalling.

Models of Proportional Problem Situations Models allow students to develop rich representations of problem situations. They can involve concrete materials, graphic designs or abstract ideas. We used. . . • Cuisenaire rods • Geometric shapes • Cardboard strips and • Double-number lines.

Models of Proportional Problem Situations: The Double Number line Using a double number line enables learners to represent proportional situations graphically.

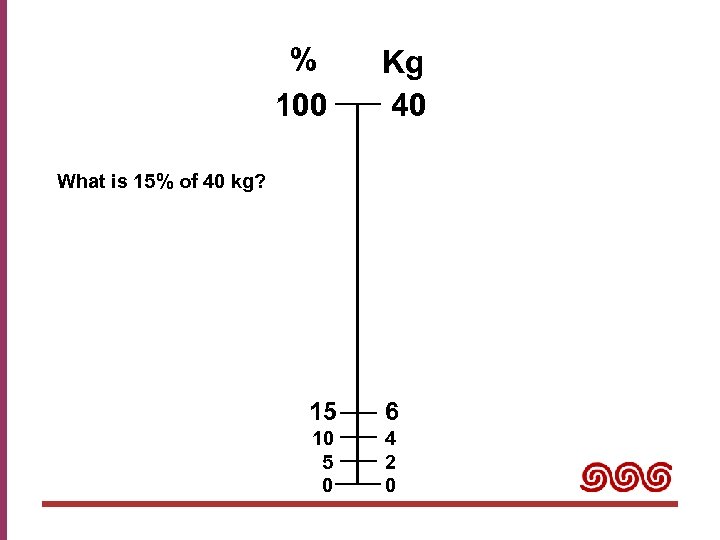% 100 Kg 40 What is 15% of 40 kg? 15 6 10 5 0 4 2 0

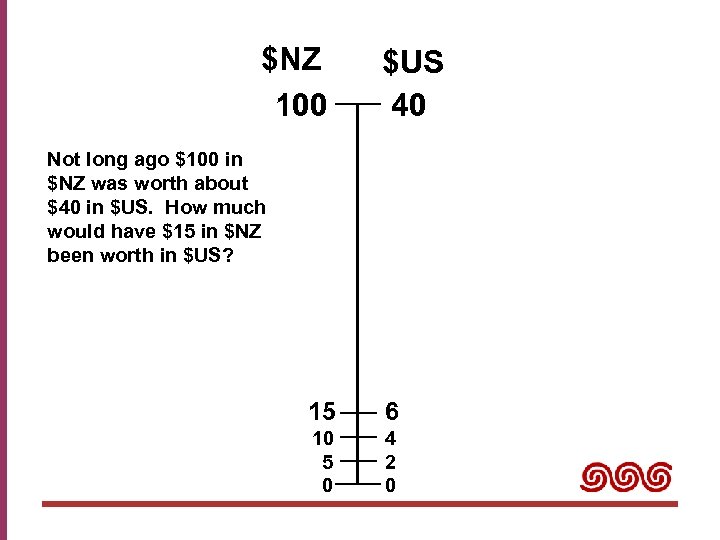$NZ 100 $US 40 Not long ago $100 in $NZ was worth about $40 in $US. How much would have $15 in $NZ been worth in $US? 15 6 10 5 0 4 2 0

Models of Proportional Problem Situations: The Double Number line The double number line was introduced through a series of ‘concrete’ activities centred on 2 -litre milk containers. For example: Drawing/creating scales showing % and capacity Identifying faulty scales Verifying scales Estimating how full a number of bottles were

Student Explanations

Models of Proportional Problem Situations: The Double Number line

Models of Proportional Problem Situations: The Double Number line When the double number line was established we observed: • Rich discourse • Students comparing methods • Students recognising patterns and strategies from analogous problems. • Students verifying answers. … all important components of SRL

Reflective Journals: Explanations

Reflective Journals: Conversations

Self Regulated Learners in Mathematics If students in mathematics are going to become self-regulated learners, they need to be confronted with opportunities that allow them to reveal their thinking and to observe and emulate thinking of others.

Kaleidoscope of Experiences