Self-Blindable Credential Certificates from the Weil Pairing Eric

Self-Blindable Credential Certificates from the Weil Pairing Eric R. Verheul April 9, 2004 SCLab Jinhae Kim

Introduction I • What is pseudonym? – A unique identifier by which a user is known by a certain party. Same user, different pseudonym. • A pseudonymous certificate binds a user’s pseudonym to his public key. • A credential is a trust provider’s statement about the user. – Example: “lives in MN”, “has a Ph. D in CS” – single-use/multiple-use

Introduction II • Credential pseudonymous certificates (CPCs) – Digital certificates that bind credentials to users. • In Chaum’s 1 model – Pseudonyms are unlinkable. • parties that know a user by different pseudonyms must not have the ability to combine their logs. – CPCs must be translatable. • CPC A: “p 1 is in good health. ” • A is issued by Dr. Yongdae under p 1. • Jinhae (owner of p 1) presents A to insurance company under p 2. 1. D. Chaum, Security Without Identification: Transaction Systems to Make Big Brother Obsolete, Communications of the ACM, 1985

Security Requirement • Protection against pseudonym/credential forgery. • Protection against pseudonym/credential sharing. – smartcard based passports – better solution: all-or-nothing – Problems? • Revocation of pseudonymous certificates and credentials.

Building Blocks I • Diffie-Hellman (DH) problem – generator g of a group G of (prime) order q. – DHg(gx, gy) = gxy • Decision Diffie-Hellman (DDH) problem – given a, b, c G decide whether c = DHg(a, b) – An alternative formulation of DDH: • given g, gx, h, hy in group G decide whether x = y. • hy = DHg(gx, h) (suppose h = ga, then gay = gax) • Group in which the DDH problem is simple and DH, DL are hard.

Building Blocks II • Elliptic Curve Cryptography 1 (ECC) – EC can provide versions of PK methods – In some case, EC is faster and use smaller key. – Addition in EC is same as multiplication in Zp* Zp * Multiplication (ab = c (mod p)) Exponentiation (ab = c (mod p)) EC Addition (X + Y = Z) Multiplication (αX = Y) ref) a, b, c Zp* X, Y are points on an elliptic curve and α is constant. 1. David Jablon, Elliptic Curve Cryptography, http: //world. std. com/dpj/elliptic. html

Building Block III • DDH in ECC – <P> is a group of (prime) order q on the curve. – A, B, C is an instance of the DDH problem with respect to P. – C = DHP(A, B) iff eq(A, D(B)) = eq(P, D(C)) – D(. ) is the distortion map, and eq(. , . ) is the Weil pairing. • Bilinear Map – B(gx, gy) = B(g, g)xy (= B(g, gxy)) (DDH is solved!) – In ECC: B(a. P, b. P) = ab B(P, P) (= B(P, ab. P))

The ‘Proofless’ Variant of the Chaum-Pedersen Scheme 1 • A group, G, of prime order q, with generator g. – the DDH problem is simple, while the DL and the DH problems are practically intractable. • the Chaum-Pedersen scheme – The public key is y = gx, where 0 ≤ x < q. – A signature on a message m ∈ G • z = mx (plus a proof that logg(y) = logm(z)). • Can verify logg(y) = logm(z) iff z = DHg(m, y). 1. D. Chaum, T. P. Pedersen, Wallet Databases with Observers, Proceedings of Crypto’ 92

The variant of C-P scheme II • Signature z = mx is self-blindable. – Without knowing of the signing key x, one can make another signature zk = (mk)x. • Easy blinding property. – Message (typically a hash), M – public key of signing party gx – Ask to sign Mr, for 0 ≤ r < q, resulting in Mrx.

Self-blindable Certificates • Terminology for Self-blindable certificates – U : collection of all possible public keys. – T : collection of all verification public keys of TP. – C : collection of all possible certificates. – Credential on a user public key PU ∈ U • {PU, Sig(PU, ST)}, ST is private signing key of TP. • Accompanied by a higher-level certificate – Cert(PU, “Trust statement”) • Standard X. 509 certificate with the “Trust statement” in one of its extension field.

Self-blindable Certificates II • The certificates are called self-blindable, if: – There exists a set transformation factor space F. – An efficiently computable transformation map • D: C ×F → C Properties 1. For any certificate C ∈ C and f ∈ F the certificate D(C, f) is signed with the same trust provider public key as C. 2. Let C 1, C 2 be certificates and f ∈ F known. If C 2 = D(C 1, f) then one can efficiently compute a transformation factor f΄∈ F such that C 1 = D(C 2, f΄). 3. If C 1, C 2 ∈ C are two different certificates on the same user public key, 4. then so are D(C 1, f) and D(C 2, f). 4. Let PU is user public key, f ∈ F is known. Then, a user possesses the 5. private key of PU iff it possesses the private key of D(PU, f). 5. If the user’s public key PU ∈ U is fixed and if f ∈ F is a uniformly random 6. element in F, then D(PU, f) is a uniformly random element in U.

CPC System • pseudonymous credential – {PU, [Sig(PU, SN), Cert(PN, “PP statement”)]} • PU : the public key of the user. • Sig(PU, SN) : a signature of the pseudonym provider (PP). • Cert(PN, “PP statement”) : a (conventional) certificate on the public verification key of the PP. – With a statement on its applicability included among the usual fields (e. g. , expiration date). – The pseudonym of a user is in fact the user’s public key in its certificate.

CPC System II • Generation of a new Pseudonymous certificate. – By choosing a (random) factor and transforming an initially issued pseudonymous certificate. – Credential Pseudonymous Certificate • Based on Pseudonymous Credential • {PU, [Sig(PU, SN), Cert(PN, “PP statement”)], [Sig(PU, SC), Cert(PC, “CP statement”)]+}. • 2 nd line: credential field. – Sig(PU, SC) : A signature of the credential provider (CP). – In CP statement: a statement on its credential applicability (e. g. , “is over 18 years old”).

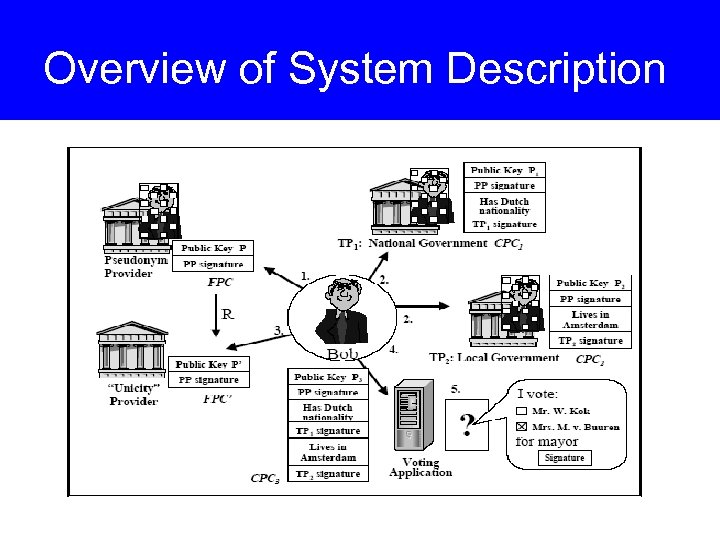
Overview of System Description

High-level System Description • Initial Registration. – The user registers, typically in a non-anonymous fashion, with a pseudonym provider. – After registration a First Pseudonymous Certificate (FPC) is issued. – The pseudonym provider puts the FPC in a public directory. – When unique pseudonyms are required, the provider has the option to maintain a private list of physical persons that were issued a pseudonymous certificate.

System Description II • Credential Issuance. – Transforms its FPC into a random pseudonymous certificates (RPC) by using a random transformation factor. – Registers with a CP using this RPC which includes a proof of possession of the private key. – This registration need not be anonymous. The user does what is required to obtain a credential (e. g. , takes a driver’s exam, shows other credentials). – Up-on succeeding, the user is issued a credential on the RPC, that is the CPC. – The pseudonym provider has the option to put the CPC in a public directory.

System Description III • Credential Use. – The user registers (typically anonymously) with a service provider using a new RPC. • If I can make an RPC with my FPC, how about others? – The user combines all of the CPCs relating to credentials required by the SP into one CPC under the registered pseudonym. • The second invert transformation property on the transformation factors related with the individual, original CPCs. • A CPC is first translated to the First Pseudonym and then translated to the registered pseudonym. • This certificate is presented to the SP, together with a proof of possession of the private key referenced in this CPC.

System Description IV • Credential Use II – Double spend checking • SP has the option to require that the user contact a specific trust provider (unicity provider). • The user sends this trust provider the transformation factor(s), transforming the new RPC to the FPC. • The trust provider validates that these factor(s) transform the RPC into a FPC on the PP’s directory, and that this FPC was not registered before. - problems? • Note 1: PP directory does not specify user identities, only FPCs, • Note 2: the specific trust provider need not be the user’s pseudonym provider.

System Description V • TP can link two different pseudonyms of a user. – During registration, PP and the user (U) exchange a secret, S. – If a trust provider (T) wants to provide assurance on unique pseudonyms, then PP is provided a list consisting of transformed FPCs, in such a way that: • U’s FPC is transformed using a transformation factor f: – f = H (T, S) (H: secure hash function) • the order of the FPCs is randomly permuted.

Revocation of Certificate Bases • 1 st Method: Pro-active – Let the trust providers employ signing keys with a short expiration time (e. g. , a week). – If a pseudonymous certificate/credential has not been revoked, then the trust provider automatically updates the certificates/credentials in its directory with newly signed ones. – A user can collect the updated pseudonymous certificates/credentials, preferably via an anonymous channel.

Revocation II • 2 nd Method: using the flexible secret sharing technique – To trust provider, send along specific transformation factors with a (credential) pseudonymous certificate. – TP can retrieve the original issued (credential) pseudonymous certificates and find out if they have been revoked. – The trust provider then provides a statement on the status of the (credential) pseudonymous certificate to the service provider. – The service provider still needs to verify that the user is in possession of the private key referenced in the used randomized CPC.

A Simple Construction for CPCs • G = <g> be a group of prime order q • The set T of all trust provider’s public keys takes the form j, js (0 ≤ s < q; private key). • U consists of elements of the form gx. (0 < x < q; user’s private keys). • A certificate issued by a trust provider with public key h, hz on a user public key gx : – {gx, gxz}. • The transformation D: C ×F → C – ({X, Y }, f) → {Xf , Yf} • the certificate {gx, gxz} is transformed to the certificate {gxf, gxfz} under factor f.

A Simple Construction II 1. The user registers, typically in a non-anonymous fashion, with a pseudonym provider. 2. The PP generates a random 0 < x < q – – – forms the user public key gx and the certificate {gx, gxz}. All information is put on a tamper resistant signing device. Private key information of (transformed) certificates can be used but not retrieved. 3. The secure signing device is handed over to the user in a secure fashion.

A more robust construction • G = <g> be a group of prime order q • There exists embedding E(. ) from G into a group G΄ where all three problems are practically intractable. • The set T of all trust provider’s public keys takes the form j, js (0 ≤ s < q; private key). • PP publishes a certified pair (r , s) = (r , rf ) – r , s∈ G, 0 < f < q unknown by all parties. • U consists of elements of the form g 1, g 2, g 1 x 1 , g 2 x 2. – 0 < x 1, x 2 < q, – g 1 is random generator and logg 1(g 2) = f

A more robust construction II • The certificate with public key h, hz on a user’s public key g 1, g 2, g 1 x 1 g 2 x 2 : – {g 1, g 2, g 1 x 1 g 2 x 2, (g 1 x 1 g 2 x 2)z}. • The transformation D: C ×F → C – ({X, Y, W, Z }, (k, l)) → {Xl, Yl , Wkl, Zkl} • the certificate {g 1, g 2, g 1 x 1 g 2 x 2, (g 1 x 1 g 2 x 2)z} is transformed to the certificate {g 1 l, g 2 l, g 1 x 1 klg 2 x 2 kl, (g 1 x 1 klg 2 x 2 kl)z} under factor (k, l).

A more robust construction III 1. The user registers, typically in a non-anonymous fashion, with a PP. 2. PP generates a random pair (g 1, g 2) – g 2 = g 1 f (random power of the elements r , s). – The pair (g 1, g 2) is sent to the user or a smart card issuer. 3. The user generates a random private key 0 ≤ x < q and forms g 2 x. – Sends g 2 x and proves possession of the private key x 4. PP forms the public key g 1, g 2, g 1 g 2 x – – – Places a Chaum-Pedersen signature on it, i. e. , (g 1 g 2 x)z. Employs the embedding E : G → G΄ Determines the elements E(g 2), E(g 2 x) of the group G΄. Determines a random power r of these elements, i. e. , E(g 2)r, E(g 2 x)r. Forms a conventional non-repudiation certificate on (E(g 2)r, E(g 2 x)r). The first pseudonymous certificate and the non-repudiation certificate are issued to the user. Both are also stored in separate directories.

A more robust construction IV • The characteristic of embedding E(. ) – Homomorphism: The signing key of E(g 2 x )r is x. – One-way function: Hard to get g 2 r, g 2 xr from E(g 2)r, E(g 2 x)r. • It would be impossible to relate E(g 2), E(g 2 x) (deducible from FPC) to E(g 2)r, E(g 2 x)r (deducible from the non-repudiation certificate). (DDH is hard in G΄)

Protection against Pseudonym/credential forgery • Based on an all-or-nothing concept. • The private key in a transformed credential takes the form (k, k · x mod q) for some 0 < k < q. • Dividing the second part by the first part yields the user’s non-repudiation key x. • If the user transfers a credential, then it also transfers a copy of its non-repudiation signing key.

Conclusion • Anonymity without the need for a trusted third party. • This system is based on a new paradigm, self-blindable certificates • Certificates were constructed using the Weil pairing in supersingular elliptic curves • A robust system provides cryptographic protection against the forgery and transfer of credentials