Self-Adjusting Computation Umut Acar Carnegie Mellon University Joint

Self-Adjusting Computation Umut Acar Carnegie Mellon University Joint work with Guy Blelloch, Robert Harper, Srinath Sridhar, Jorge Vittes, Maverick Woo 14 January 2004 Workshop on Dynamic Algorithms and Applications

Dynamic Algorithms Maintain their input-output relationship as the input changes Example: A dynamic MST algorithm maintains the MST of a graph as user to insert/delete edges Useful in many applications involving interactive systems, motion, . . . 14 January 2004 Workshop on Dynamic Algorithms and Applications 2

Developing Dynamic Algorithms: Approach I Dynamic by design Many papers Agarwal, Atallah, Bash, Bentley, Chan, Cohen, Demaine, Eppstein, Even, Frederickson, Galil, Guibas, Henzinger, Hershberger, King, Italiano, Mehlhorn, Overmars, Powell, Ramalingam, Roditty, Reif, Reps, Sleator, Tamassia, Tarjan, Thorup, Vitter, . . . Efficient algorithms but can be complex 14 January 2004 Workshop on Dynamic Algorithms and Applications 3

Approach II: Re-execute the algorithm when the input changes Very simple General Poor performance 14 January 2004 Workshop on Dynamic Algorithms and Applications 4

Smart re-execution Suppose we can identify the pieces of execution affected by the input change Re-execute by re-building only the affected pieces Execution (A, I) Execution (A, I+e) 14 January 2004 Workshop on Dynamic Algorithms and Applications 5

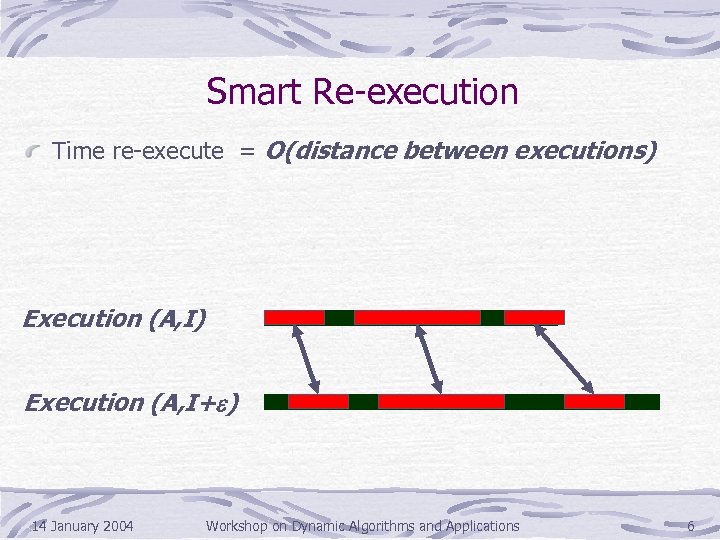Smart Re-execution Time re-execute = O(distance between executions) Execution (A, I+e) 14 January 2004 Workshop on Dynamic Algorithms and Applications 6

Incremental Computation or Dynamization General techniques for transforming algorithms dynamic Many papers: Alpern, Demers, Field, Hoover, Horwitz, Hudak, Liu, de Moor, Paige, Pugh, Reps, Ryder, Strom, Teitelbaum, Weiser, Yellin. . . Most effective techniques are Static Dependence Graphs [Demers, Reps, Teitelbaum ‘ 81] Memoization [Pugh, Teitelbaum ‘ 89] These techniques work well for certain problems 14 January 2004 Workshop on Dynamic Algorithms and Applications 7

Bridging the two worlds Dynamization simplifies development of dynamic algorithms but generally yields inefficient algorithms Algorithmic techniques yield good performance Can we have the best of the both worlds? 14 January 2004 Workshop on Dynamic Algorithms and Applications 8

Our Work Dynamization techniques: Dynamic dependence graphs [Acar, Blelloch, Harper ‘ 02] Adaptive memoization [Acar, Blelloch, Harper ‘ 04] Stability: Technique for analyzing performance [ABHVW ‘ 04] Provides a reduction from dynamic to static problems Reduces solving a dynamic problem to finding a stable solution to the corresponding static problem Example: Dynamizing parallel tree contraction algorithm [Miller, Reif 85] yields an efficient solution to the dynamic trees problem [Sleator, Tarjan ‘ 83], [ABHVW SODA 04] 14 January 2004 Workshop on Dynamic Algorithms and Applications 9

Outline Dynamic Dependence Graphs Adaptive Memoization Applications to Sorting Kinetic Data Structures with experimental results Retroactive Data Structures 14 January 2004 Workshop on Dynamic Algorithms and Applications 10

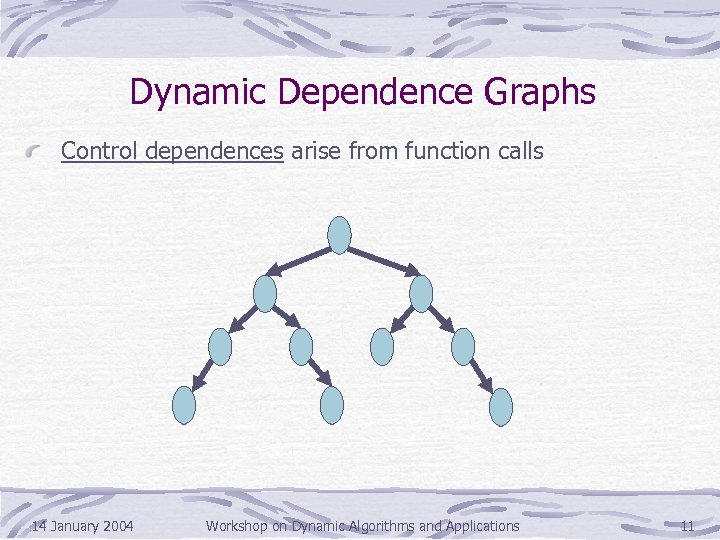Dynamic Dependence Graphs Control dependences arise from function calls 14 January 2004 Workshop on Dynamic Algorithms and Applications 11

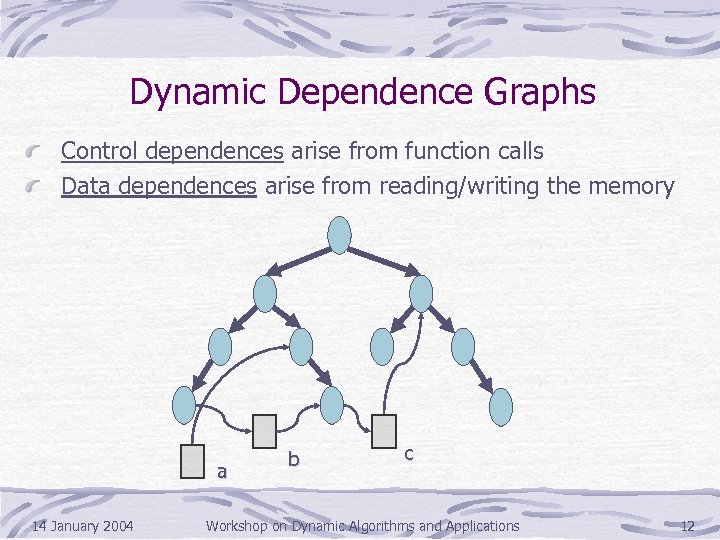Dynamic Dependence Graphs Control dependences arise from function calls Data dependences arise from reading/writing the memory a 14 January 2004 b c Workshop on Dynamic Algorithms and Applications 12

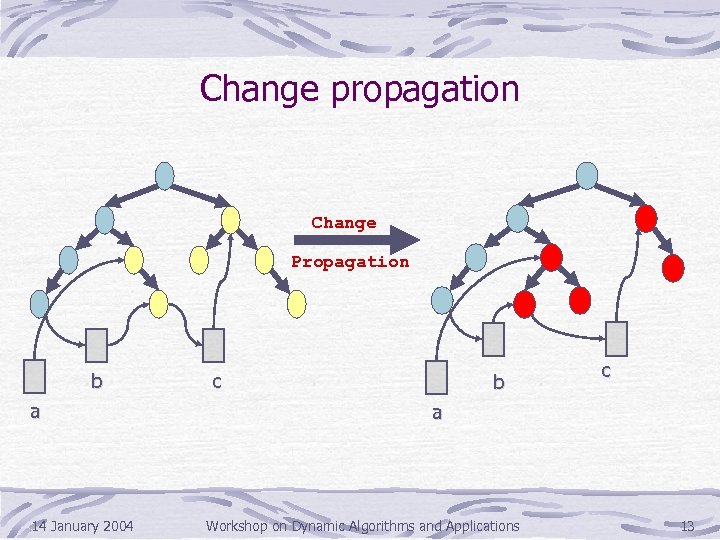Change propagation Change Propagation b a 14 January 2004 c b c a Workshop on Dynamic Algorithms and Applications 13

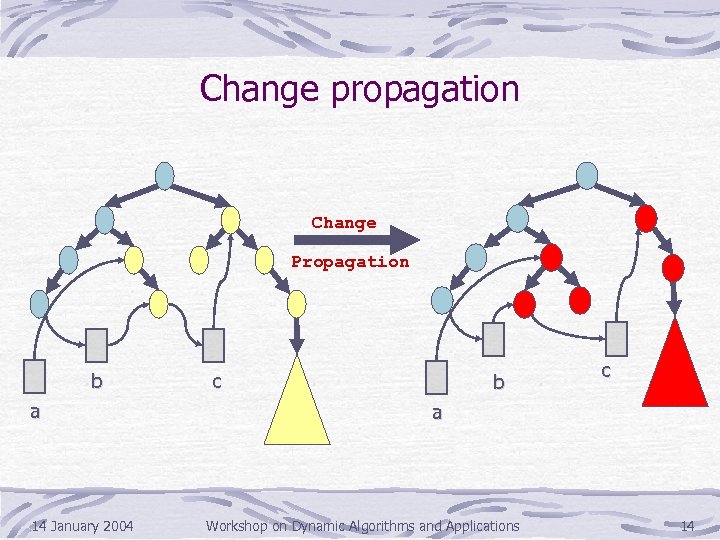Change propagation Change Propagation b a 14 January 2004 c b c a Workshop on Dynamic Algorithms and Applications 14

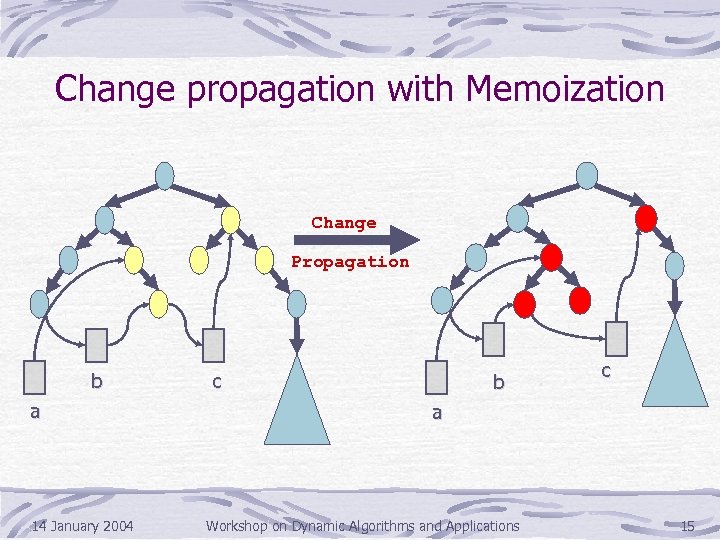Change propagation with Memoization Change Propagation b a 14 January 2004 c b c a Workshop on Dynamic Algorithms and Applications 15

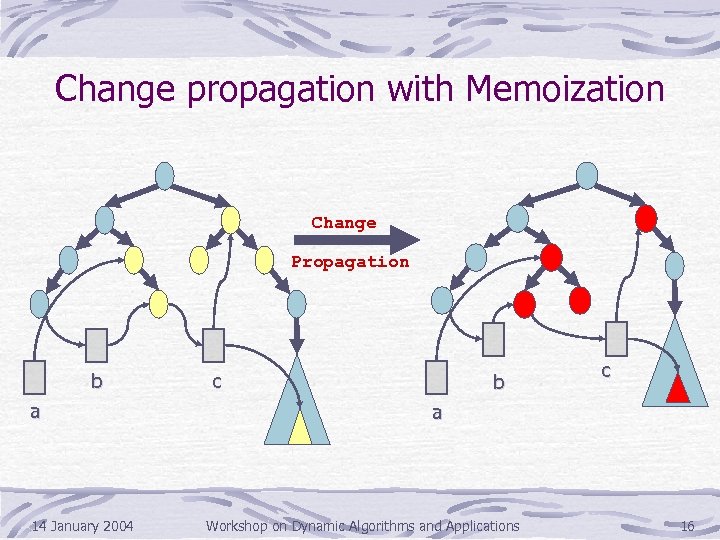Change propagation with Memoization Change Propagation b a 14 January 2004 c b c a Workshop on Dynamic Algorithms and Applications 16

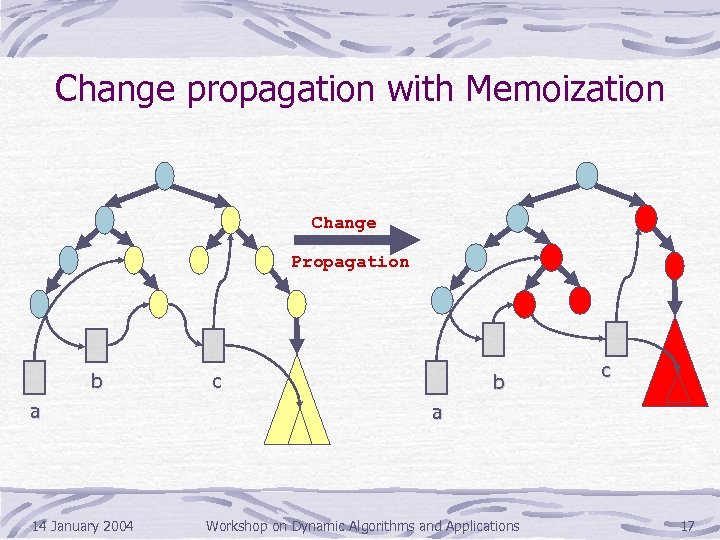Change propagation with Memoization Change Propagation b a 14 January 2004 c b c a Workshop on Dynamic Algorithms and Applications 17

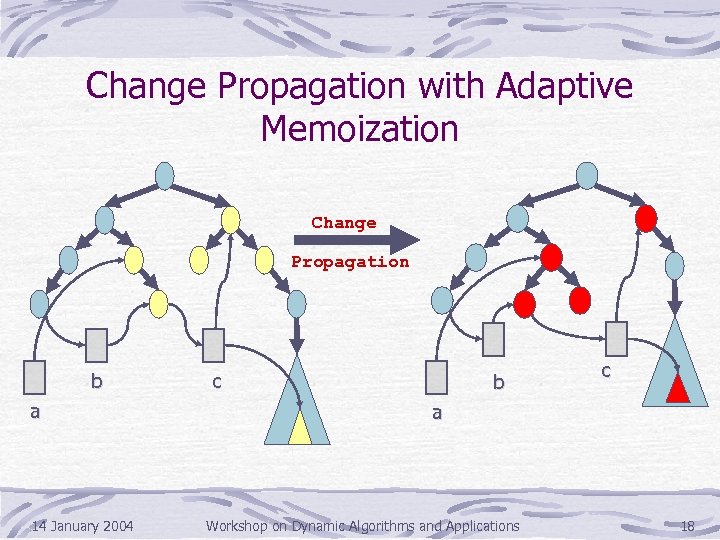Change Propagation with Adaptive Memoization Change Propagation b a 14 January 2004 c b c a Workshop on Dynamic Algorithms and Applications 18

The Internals 1. Order Maintenance Data Structure [Dietz, Sleator ‘ 87] Time stamp vertices of the DDG in sequential execution order 2. Priority queue for change propagation priority = time stamp Re-execute functions in sequential execution order Ensures that a value is updated before being read 3. Hash tables for memoization Remember results from the previous execution only 4. Constant-time equality tests 14 January 2004 Workshop on Dynamic Algorithms and Applications 19

Standard Quicksort fun qsort (l) = let fun qs (l, rest) = case l of NIL => rest | CONS(h, t) => let (smaller, bigger) = split(h, t) sbigger = qs (bigger, rest) in qs (smaller, CONS(h, sbigger)) end in qs(l, NIL) end 14 January 2004 Workshop on Dynamic Algorithms and Applications 20

Dynamic Quicksort fun qsort (l) = let fun qs (l, rest, d) = read(l, fn l' => case l' of NIL => write (d, rest) | CONS(h, t) => let (less, bigger) = split (h, t) sbigger = mod (fn d => qs(bigger, rest, d)) in qs(less, CONS(h, sbigger, d)) end in mod (fn d => qs (l, NIL, d)) end 14 January 2004 Workshop on Dynamic Algorithms and Applications 21

Performance of Quicksort Dynamized Quicksort updates its output in expected O(logn) time for insertions/deletions at the end of the input O(n) time for insertions/deletions at the beginning of the input O(logn) time for insertions/deletions at a random location Other Results for insertions/deletions anywhere in the input Dynamized Mergesort: expected O(logn) Dynamized Insertion Sort: expected O(n) Dynamized minimum/maximum/sum/. . . : expected O(logn) 14 January 2004 Workshop on Dynamic Algorithms and Applications 22

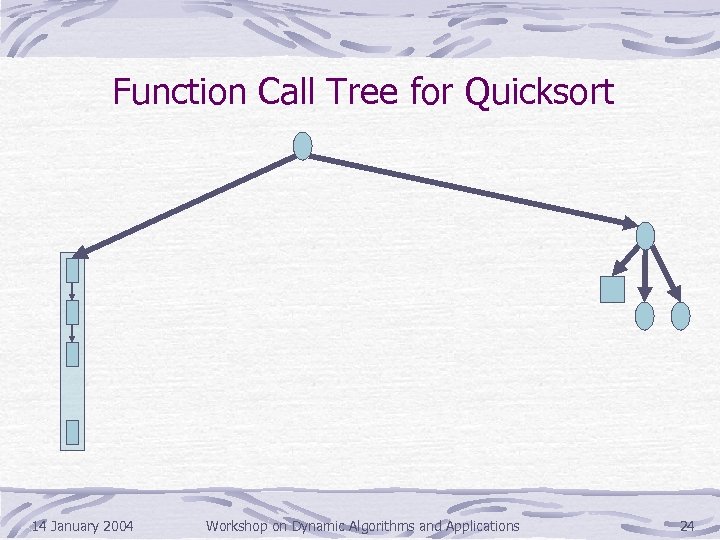
Function Call Tree for Quicksort 14 January 2004 Workshop on Dynamic Algorithms and Applications 23

Function Call Tree for Quicksort 14 January 2004 Workshop on Dynamic Algorithms and Applications 24

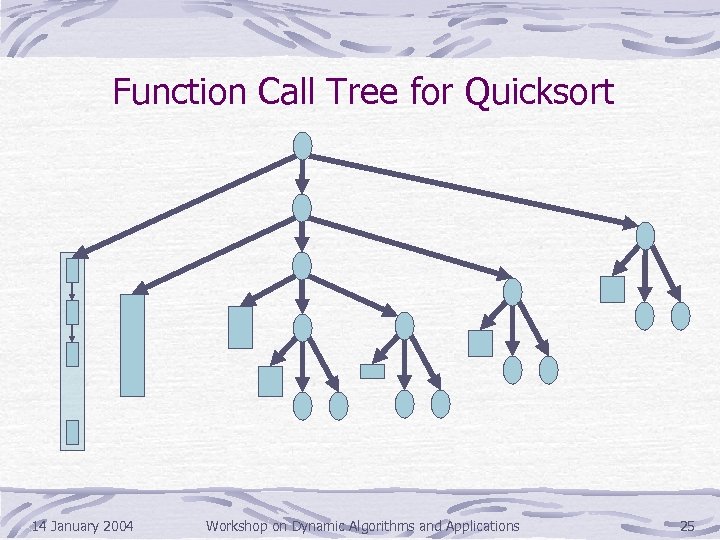Function Call Tree for Quicksort 14 January 2004 Workshop on Dynamic Algorithms and Applications 25

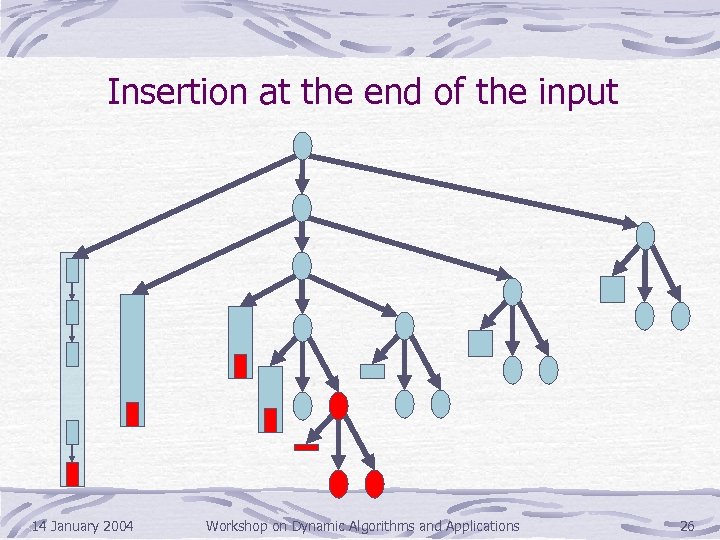Insertion at the end of the input 14 January 2004 Workshop on Dynamic Algorithms and Applications 26

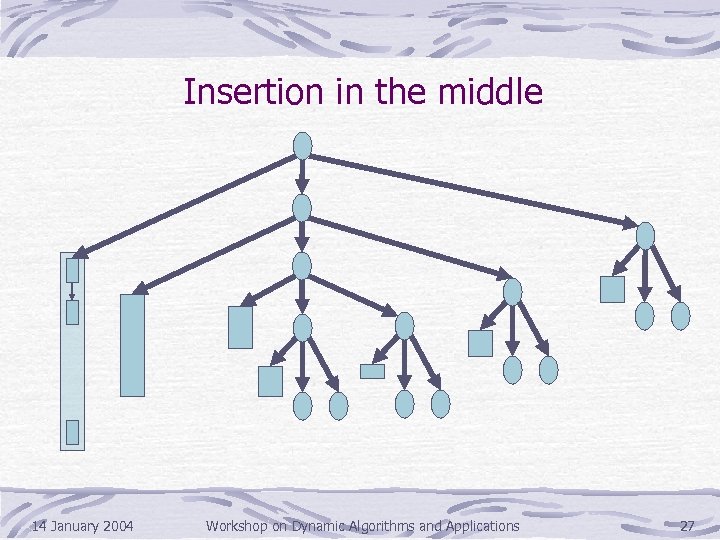Insertion in the middle 14 January 2004 Workshop on Dynamic Algorithms and Applications 27

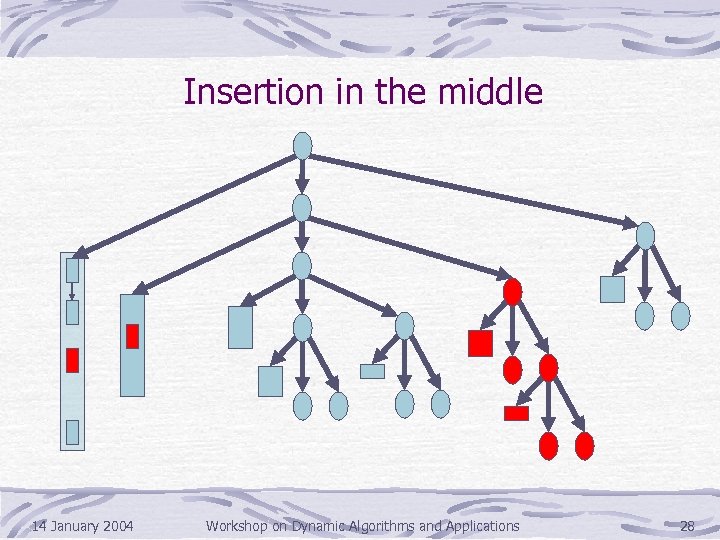Insertion in the middle 14 January 2004 Workshop on Dynamic Algorithms and Applications 28

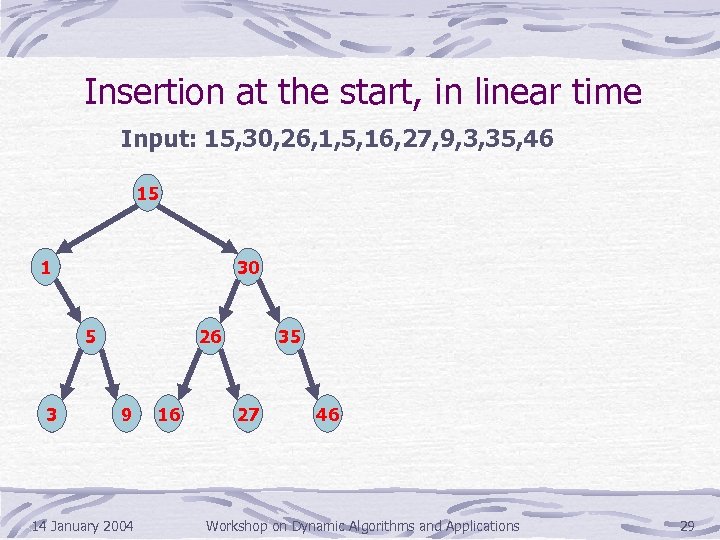Insertion at the start, in linear time Input: 15, 30, 26, 1, 5, 16, 27, 9, 3, 35, 46 15 1 30 5 3 26 9 14 January 2004 16 35 27 46 Workshop on Dynamic Algorithms and Applications 29

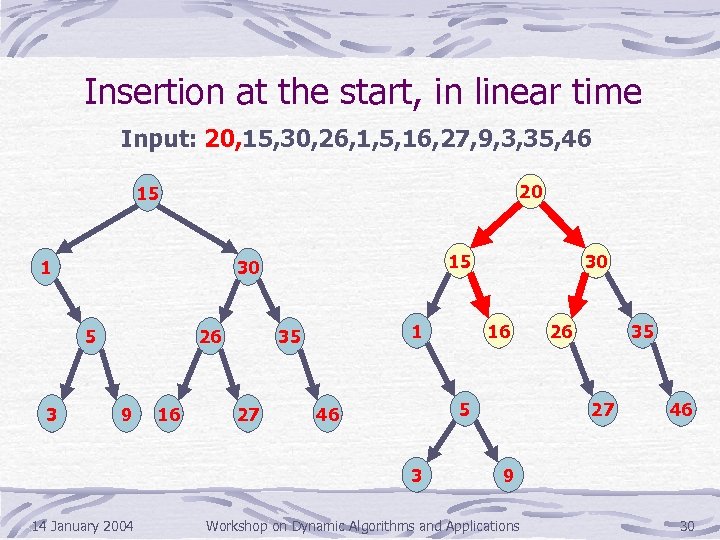Insertion at the start, in linear time Input: 20, 15, 30, 26, 1, 5, 16, 27, 9, 3, 35, 46 20 15 1 5 3 15 30 26 9 16 1 35 27 16 5 46 3 14 January 2004 30 26 35 27 46 9 Workshop on Dynamic Algorithms and Applications 30

Kinetic Data Structures [Basch, Guibas, Herschberger ‘ 99] Goal: Maintain properties of continuously moving objects Example: A kinetic convex-hull data structure maintains the convex hull of a set of continuously moving objects 14 January 2004 Workshop on Dynamic Algorithms and Applications 31

Kinetic Data Structures Run a static algorithm to obtain a proof of the property Certificate = Comparison + Failure time Insert the certificates into a priority queue Priority = Failure time while queue ¹ empty do { certificate = remove (queue) flip (certificate) update the certificate set (proof) } A framework for handling motion [Guibas, Karavelas, Russel, ALENEX 04] 14 January 2004 Workshop on Dynamic Algorithms and Applications 32

Kinetic Data Structures via Self-Adjusting Computation Update the proof automatically with change propagation while queue ¹ empty do { certificate = remove (queue) flip (certificate) propagate ()} A library for kinetic data structures [Acar, Blelloch, Vittes] Quicksort: expected O(1), Mergesort: expected O(1) Quick Hull, Chan’s algorithm, Merge Hull: expected O(logn) 14 January 2004 Workshop on Dynamic Algorithms and Applications 33

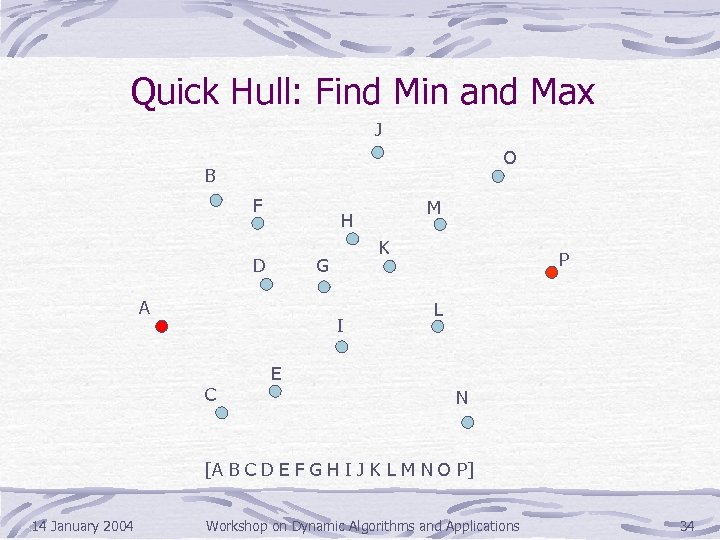Quick Hull: Find Min and Max J O B F D K G A I C M H P L E N [A B C D E F G H I J K L M N O P] 14 January 2004 Workshop on Dynamic Algorithms and Applications 34

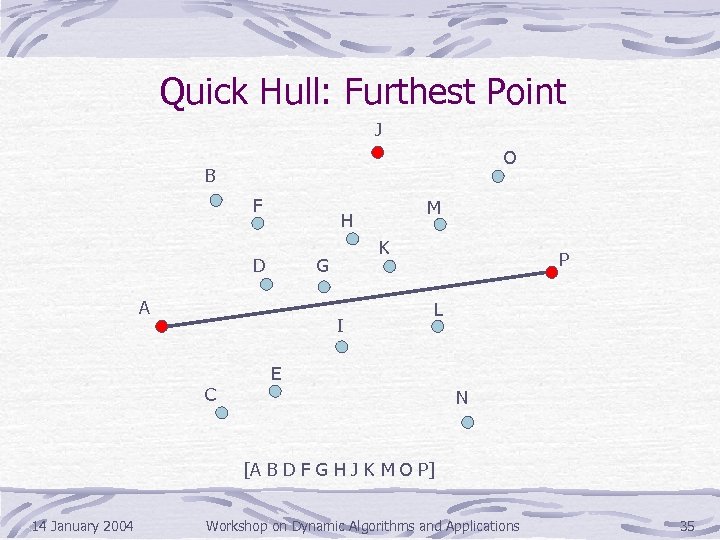Quick Hull: Furthest Point J O B F D K G A I C M H P L E N [A B D F G H J K M O P] 14 January 2004 Workshop on Dynamic Algorithms and Applications 35

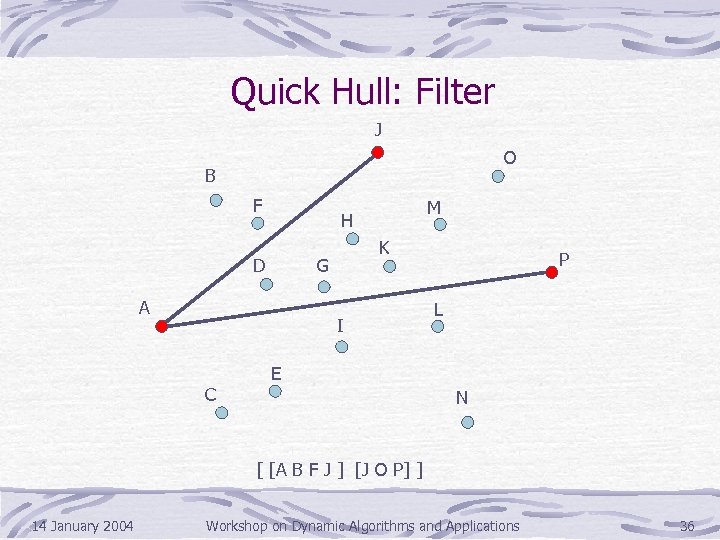Quick Hull: Filter J O B F M H D K G A I C P L E N [ [A B F J ] [J O P] ] 14 January 2004 Workshop on Dynamic Algorithms and Applications 36

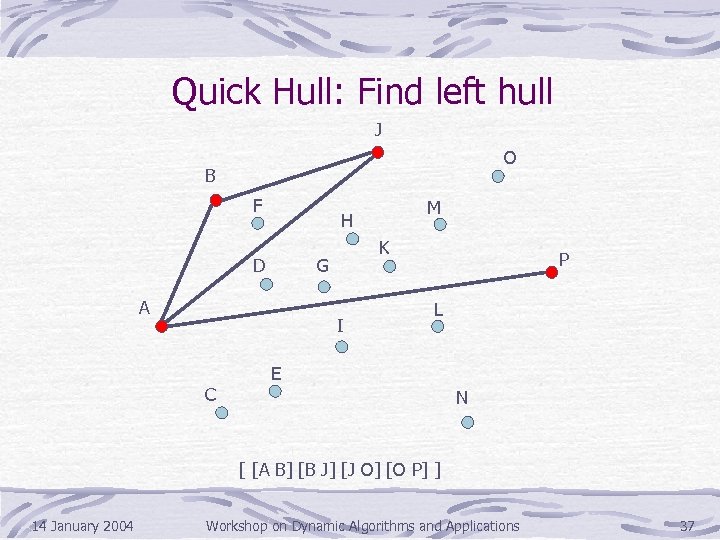Quick Hull: Find left hull J O B F D K G A I C M H P L E N [ [A B] [B J] [J O] [O P] ] 14 January 2004 Workshop on Dynamic Algorithms and Applications 37

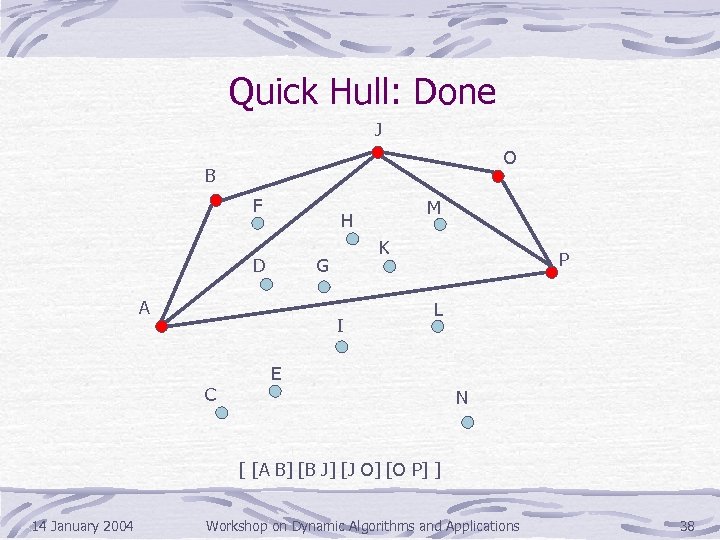Quick Hull: Done J O B F D K G A I C M H P L E N [ [A B] [B J] [J O] [O P] ] 14 January 2004 Workshop on Dynamic Algorithms and Applications 38

Static Quick Hull fun find. Hull(line as (p 1, p 2), l, hull) = let pts = filter l (fn p => Geo. lineside(p, line)) in case pts of EMPTY => CONS(p 1, hull) | _ => let pm = max (Geo. dist line) l left = find. Hull((pm, p 2), l, hull, dest) full = find. Hull((p 1, pm), l, left) in full end fun quick. Hull l = let (mx, xx) = minmax (Geo. min. X, Geo. max. X) l in find. Hull((mx, xx), points, CONS(xx, NIL) end 14 January 2004 Workshop on Dynamic Algorithms and Applications 39

Kinetic Quick Hull fun find. Hull(line as (p 1, p 2), l, hull, dest) = let pts = filter l(fn p => Kin. lineside(p, line)) in modr (fn dest => read l (fn l => case l of NIL => write(dest, CONS(p 1, hull)) | _ => read (max (Kin. dist line) l) (fn pm => let gr = modr (fn d => find. Hull((pm, p 2), l, hull, d)) in find. Hull((p 1, pm), l, gr, dest)))) end fun quick. Hull l = let (mx, xx) = minmax (Kin. min. X, Kin. max. X) l in modr(fn d => read (mx, xx)(fn (mx, xx) => split ((mx, xx), l, CONS(xx, NIL), d)))) end 14 January 2004 Workshop on Dynamic Algorithms and Applications 40

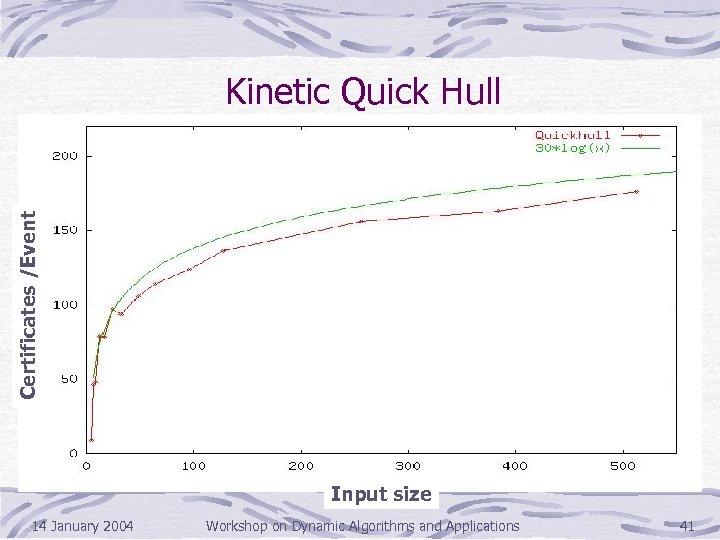Certificates /Event Kinetic Quick Hull Input size 14 January 2004 Workshop on Dynamic Algorithms and Applications 41

Dynamic and Kinetic Changes Often interested in dynamic as well as kinetic changes Insert and delete objects Change the motion plan, e. g. , direction, velocity Easily programmed via self-adjusting computation Example: Kinetic Quick Hull code is both dynamic and kinetic Batch changes Real time changes: Can maintain partially correct data structures (stop propagation when time expires) 14 January 2004 Workshop on Dynamic Algorithms and Applications 42

Retroactive Data Structures [Demaine, Iacono, Langerman ‘ 04] Can change the sequence of operations performed on the data structure Example: A retroactive queue would allow the user to go back in time and insert/remove an item 14 January 2004 Workshop on Dynamic Algorithms and Applications 43

Retroactive Data Structures via Self-Adjusting Computation Dynamize the static algorithm that takes as input the list of operations performed Example: retroactive queues Input: list of insert/remove operations Output: list of items removed Retroactive change: change the input list and propagate 14 January 2004 Workshop on Dynamic Algorithms and Applications 44

Rake and Compress Trees [Acar, Blelloch, Vittes] Obtained by dynamizing tree contraction [ABHVW ‘ 04] Experimental analysis Implemented and applied to a broad set of applications Path queries, subtree queries, non-local queries etc. For path queries, compared to Link-Cut Trees [Werneck] Structural changes are relatively slow Data changes are faster 14 January 2004 Workshop on Dynamic Algorithms and Applications 45

Conclusions Automatic dynamization techniques can yield efficient dynamic and kinetic algorithms/data structures General-purpose techniques for transforming static algorithms to dynamic and kinetic analyzing their performance Applications to kinetic and retroactive data structures Reduce dynamic problems to static problems Future work: Lots of interesting problems Dynamic/kinetic/retroactive data structures 14 January 2004 Workshop on Dynamic Algorithms and Applications 46

Thank you! 14 January 2004 Workshop on Dynamic Algorithms and Applications 47