СЕКВЕНЦІЙНІ ЧИСЛЕННЯ КОМПОЗИЦІЙНО-НОМІНАТИВНИХ ЛОГІК КВАЗІАРНИХ ПРЕДИКАТІВ С C

СЕКВЕНЦІЙНІ ЧИСЛЕННЯ КОМПОЗИЦІЙНО-НОМІНАТИВНИХ ЛОГІК КВАЗІАРНИХ ПРЕДИКАТІВ С. C. Шкільняк Київський національний університет імені Тараса Шевченка Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 1

Композиційно-номінативні логіки – це програмно орієнтовані логічні формалізми, будовані на основі cпільного для логіки й програмування композиційно номінативного підходу. В доповіді пропонується спектр секвенційних числень чистих першопорядкових композиційно номінативних логік – часткових однозначних, – тотальних неоднозначних, – часткових неоднозначних квазіарних предикатів. Такі числення побудовано: – для загального випадку логік квазіарних предикатів, – для логік однозначних еквітонних предикатів, – для логік тотальних антитонних предикатів. Для побудованих числень доведено теореми коректності та повноти. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 2

1. ОСНОВНІ ПОНЯТТЯ ТА ВИЗНАЧЕННЯ Область істинності та область хибності предиката P : D {T, F} T(P) = {d D | T P(d)} F(P) = {d D | F P(d)} Якщо Р – однозначний, то T(P) F(P) = . Якщо Р – тотальний, то T(P) F(P) = D. Предикат P на D тотально істинний, якщо T(P) = D. Предикат P на D неспростовний (частково істинний) якщо F(P) = . Предикат P : D {T, F} монотонний, якщо d d' P(d) P(d'). Предикат P : D {T, F} антитонний, якщо d d' P(d) P(d'). Однозначний предикат P : D {T, F} еквітонний: d, d' D із d ' d випливає: P(d) P(d') = P(d). V іменна множина над A – це довільна однозначна функція : V A. Ф ю вигляду Р : VA {T, F} назвемо V квазіарним предикатом на A. Ім'я x V строго неістотне для V квазіарного предиката P: d VA та a A маємо P(d x a) = P(d║ х). Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 3

Логічні зв’язки , , &, , визначимо так: T( P) = F(P); F( P) = T(P). T(P Q) = T(P) T(Q); F(P Q) = F(P) F(Q). T(P&Q) = T(P) T(Q); F(P&Q) = F(P) F(Q). T(P Q) = F(P) T(Q); F(P Q) = T(P) F(Q). T(P Q) = (T(P) T(Q)) (F(P) F(Q)); F(P Q) = (T(P) F(Q)) (F(P) T(Q)). Параметричну операцію реномінації визначимо так: = [v 1 (x 1), . . . , vn (xn)] ( ║(V{v 1, . . . , vn})). Композицію реномінації Pr. А визначаємо так: Композиція квантифікації x : Pr. А визначається так: T( x. P) = {d VA | T Р(d x a) для деякого a A}, F( x. P) = {d VA | F Р(d x a) для всіх a A}. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 4

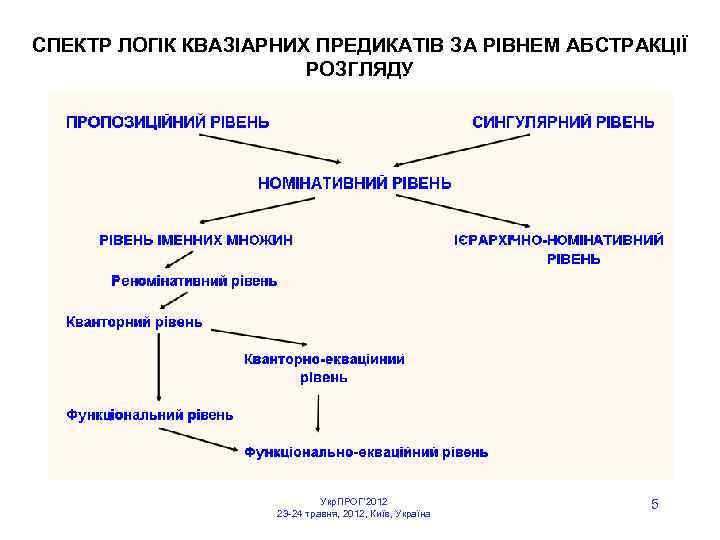СПЕКТР ЛОГІК КВАЗІАРНИХ ПРЕДИКАТІВ ЗА РІВНЕМ АБСТРАКЦІЇ РОЗГЛЯДУ Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 5

Класична логіка є логікою скінченно арних тотальних предикатів. До класичної найближчі догіки повнототальних еквітонних предикатів. Вони зберігають основні закони класичної логіки. Логіки еквітонних предикатів підпорядковуються основним законам класичної логіки, проте для них уже не діють деякі правила виведення (modus ponens). Логіки ЕП і ПЕП названі неокласичними через їх близькість до класичної логіки. Неокласичні розширення логік еквітонних предикатів Для локально-еквітонних предикатів вимагається збереження значення при розширенні даних лише на скінченну кількість компонент. Логіки еквісумісних та локально-еквісумісних предикатів базуються на класах предикатів, визначених на даних з неповною інформацією. Еквісумісність: за можливості розширення різних даних (сумісність даних) до одного більшого значення предиката на таких даних мають збігатися. Локально-еквісумісність: Збереження значень лише для розширень скінченною інформацією. При переході від логік ПЕП до логік ЕП, від них до логік ЛЕП та логік ЕСП, а далі до логік ЛЕСП, отримуємо все ширші класи семантичних моделей. Водночас ці логіки зберігають основні закони класичної логіки. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 6

СПЕКТР ЛОГІК ЗА ОБМЕЖЕННЯМИ НА КЛАС КВАЗІАРНИХ ПРЕДИКАТІВ Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 7

2. ЛОГІЧНЕ СЛІДУВАННЯ В КНЛ КВАЗІАРНИХ ПРЕДИКАТІВ Для логік квазіарних предикатів запропоновано різні семантики та різні формалізації відношення логічного наслідку. Для пропозиційної логіки нестандартні семантики та різноманітні відношення логічного наслідку розглядались в роботах О. Д. Смирнової. Подібні семантики та різні формалізації відношення логічного наслідку узагальнені для КНЛ часткових однозначних, тотальних та часткових неоднозначних предикатів на номінативних рівнях. Логіка тотальних однозначних предикатів – це класична логіка. Логіки однозначних часткових предикатів – це логіки з неокласичною семантикою. Логіки тотальних неоднозначних предикатів – це логіки з пересиченою семантикою. Логіки часткових неоднозначних предикатів назвемо логіками із загальною семантикою Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 8

Модель мови АС B = (A, IB) дуальна до АС A = (A, IA), якщо p Ps Тоді A = (A, IA) дуальна до B = (A, IB). Якщо A = (A, IA) – АС з частковими однозначними предикатами, то дуальна B = (A, IB) – із тотальними неоднозначними предикатами, та навпаки. Теорема. Нехай B = (A, IB) дуальна до A = (A, IA). Тоді ф-ли маємо: 1) 2) A еквітонний B антитонний; A антитонний B еквітонний. Неокласична семантика та пересичена семантика дуальні: A неспростовний на АС з частковими однозначними предикатами A B тотально істинний на дуальній АС B з тотальними неоднозначними предикатами. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 9

На базі різних співвідношень між областями істинності та хибності предикатів задамо 5 “природних” відношень. логічного наслідку. Відношення наслідку для двох формул при інтерпретації на фіксованій A: 1) Істиннісний наслідок A|=T : A|=T T( A). 2) Хибнісний наслідок A|=F : A|=F F( A). 3) Cильний наслідок A|=TF : A|=TF ( A) T( A) та F( A). 4) Неспростовнісний (неокласичний) A|=Cl : A|=Cl T( A) F( A) = . 5) Насичений наслідок A|=Cm : A|=Cm F( A) T( A) = VA. Визначаємо відповідні логічні наслідки |=T , |=F , |=TF , |=Cl , |=Cm за схемою: |= A|= для кожної АС A (тут – одне Cl, Cm, T, F, TF) Слабкий наслідок ||= : A = (A, I) A |= . Слабкий тотальний наслідок || : A = (A, I) A | . Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 10

Нехай B = (A, IB) дуальна до A = (A, IA). Тоді: A|=T B|=F , A|=F B|=T ; A|=Cl B|=Cm ; A|=Cm B |= Cl . “Природним” для неокласичної семантики є наслідок |=Cl , для пересиченої – наслідок |=Cm , для загальної – наслідок |=TF. Відношення логічного наслідку індукують відношення еквівалентності A T , A F , A TF , A Cl , A Cm та логічної еквівалентності T , F , TF , Cl , Cm. Відношення логічного наслідку поширюються на множини формул. Властивості відношень логічного наслідку досліджено в різних семантиках для загального випадку квазіарних та для випадків еквітонних і антитонних предикатів. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 11

Співвідношення для множин формул, які у відповідних відношеннях. 1. Неокласична семантика: |=TF |=T , |=TF |=F , |=T |=Cl , |=F |=Cl ; |=t |=Cl , |=F ||=, |=T || ; |=Cm = ; |=t |=T , |=t |=F , |=TF |=t ; |=T ||=, |=F || , ||= |=Cl , || |=Cl. 2. Пересичена семантика: |=TF |=T , |=TF |=F , |=T |=Cm , |=F |=Cm ; |=t |=Cm , |=F ||=, |=T || ; |=Cl = ; |=t |=T , |=t |=F , |=TF |=t ; |=T ||=, |=F || , ||= |=Cm , || |=Cm. 3. Загальна семантика: |=TF = |=T = |=F ; |=t |=TF , |=TF |=t ; |=TF || = ||= ; |=Cl = , |=Cm = . 4. Загальна семантика еквітонних чи загальна семантика антитонних: |=TF |=T , |=TF |=F ; |=t |=TF , |=TF |=t ; |=T || , |=F ||= ; |=Cl = , |=Cm = . Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 12

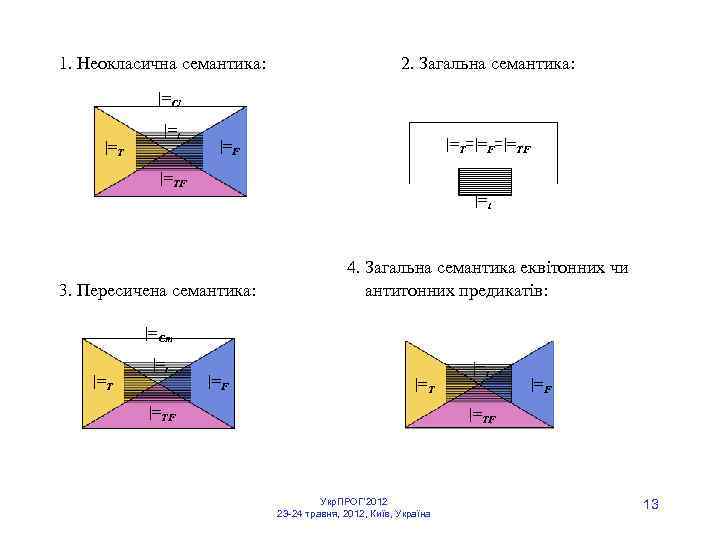1. Неокласична семантика: 2. Загальна семантика: |=Cl |=T |=t |=T=|=F=|=TF |=F |=TF |=t 4. Загальна семантика еквітонних чи 3. Пересичена семантика: антитонних предикатів: |=Cm |=T |=t |=F |=TF Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 13

3. СЕКВЕНЦІЙНІ ЧИСЛЕННЯ КНЛ КВАЗІАРНИХ ПРЕДИКАТІВ Різноманітність семантик та відношень логічного наслідку в КНЛ індукує побудову для них низки різновидностей секвенційних числень. Раніше такі числення побудовані для традиційного відношення |=Cl КНЛ однозначних квазіарних предикатів Метою роботи є побудова спектру сек. числень для відношень |=Cl, |=Cm, |=T, |=F, |=TF в КНЛ часткових однозначних, тотальних неоднозначних та часткових неоднозначних квазіарних предикатів. Основна увага – побудові першопорядкових секвенційних числень кванторного рівня (КНЛК). Такі числення пропонуються – для загального випадку логік квазіарних предикатів, – для логік еквітонних (монотонних) однозначних предикатів, – для логік антитонних тотальних предикатів. Характерна особливість цих числень – використання спеціальних секв. форм елімінації кванторів під реномінацією, що робить зайвим використання секв. форм для пронесення кванторів через реномінації. Для побудованих числень доведено теореми коректності й повноти. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 14

3. 1. Різновидності секвенційних числень КНЛ Залежно відношення логічного наслідку та семантики для КНЛ отримано низку різновидностей секвенційних числень. Числення QCl формалізує відношення: – |=Cl (неокласична семантика) для КНЛК однозначних предикатів; – |=Cm (пересичена семантика) для КНЛК тотальних предикатів. Числення QEq. Cl формалізує відношення: – |=Cl (неокласична семантика) для КНЛК однозначних ЕП; – |=Cm (пересичена семантика) для КНЛК тотальних АП. QEq. Cl – різновидність відомого неокласичного секв. числення. Числення QL формалізує відношення: – |=T (неокласична семантика) для КНЛК однозначних предикатів; – |=F (пересичена семантика) для КНЛК тотальних предикатів. Числення QEq. L формалізує відношення: – |=T (неокласична семантика) для КНЛК однозначних ЕП; – |=F (пересичена семантика) для КНЛК тотальних АП. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 15

Числення QR формалізує відношення: – |=F (неокласична семантика) для КНЛК однозначних предикатів; – |=T (пересичена семантика) для КНЛК тотальних предикатів. Числення QEq. R формалізує відношення: – |=F (неокласична семантика) для КНЛК однозначних ЕП; – |=T (пересичена семантика) для КНЛК тотальних АП. Числення QLR формалізує |=TF для КНЛК однозначних предикатів (неокласична семантика) та для КНЛК тотальних предикатів (пересичена семантика). Числення QEq. LR формалізує |=TF для КНЛК однозначних ЕП (неокласична семантика) та для КНЛК тотальних АП (пересичена семантика) Числення QGS формалізує |=TF у випадку загальної семантики часткових неоднозначних предикатів. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 16

Окремими випадками числень QCl, QL, QR, QLR, QGS для реномінативних логік є числення Rn. Cl, Rn. L, Rn. R, Rn. LR, Rn. GS. На пропозиційному рівні маємо числення Pr. Cl, Pr. L, Pr. R, Pr. LR, Pr. GS, які є окремими випадками Rn. Cl, Rn. L, Rn. R, Rn. LR, Rn. GS. Числення Pr. Cl – фактично класичне пропозиційне числення Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 17

Секвенційні числення чистих першопорядкових КНЛ |=Cl |=Cm |=T |=F |=TF _______________________________ Нео ЕП QEq. Cl – QEq. L QEq. R QEq. LR Нео QCl – QL QR QLR Пер АП – QEq. Cl QEq. R QEq. LR Пер – QCl QR QLR Загальна – QGS Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 18

Базова умова замкненості секвенції в усіх численнях – умова С: С) існує формула така, що |– та –| . Якщо секвенція |– –| замкнена, то |= . Додаткова умова Un. D замкненості секвенції в даній вершині секв. дерева індукована розподілом імен секвенції вершини дерева на означені й неозначені. Нехай U – множина всіх неозначених імен в даній вершині секв. . Секвенція U замкнена, якщо: Un. D) існує пара формул таких, що та мають однакові U неозначувані форми. Якщо |– –| U-замкнена, то A, Х–U |= для довільних A та Х V: Х U = . Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 19

Числення QGS. Замкненість секвенції визначається умовою C Un. D. Базові секвенційні форми числення QGS записуються згідно відповідних властивостей відношень |=TF. | | |–RT –|RT |– RT –| RT Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 20

|– N при у (A) |– N при у (A) |–RR |– RR –| N при у (A) –| N при у (A) –|RR –| RR |–R –|R |– R –| R Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 21

|–R –|R |– R –| R |–R R при –|R R при |– R R при –| R R при |–R p –|R p |– R p –| R p Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 22

|– R –| R Для |– R та –| R , z тотально строго неістотне та z пт( , . |– –| |– –| Для |– та –| z тотально строго неістотне та z пт( , x. А). Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 23

Секвенційні форми типів RT, N, N, R R, R p назвемо допоміжними, інші базові секвенційні форми віднесемо до основних. Форми |– R, |– , –| R, –| назвемо T формами. Форми |– R, |– , –| R, –| назвемо F формами. Форми | , | , |–RT, –|RT, |– RT, –| RT, |–RR, –|RR, |– RR, –| RR, |–R , –|R , |– R , –| R , |– N, |– N – базові сек. форми числення Rn. GS. Форми | , | , | , | – базові сек. форми числення Pr. GS. Замкненість секвенції в численнях Rn. GS та Pr. GS задається умовою С. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 24

Числення QL. Замкненість секвенції дається умовою C CL Un. D. Умова СL: СL) замкнена, якщо існує формула така, що |– та |– . Базові секвенційні форми числення QL такі ж, як і для числення QGS. Базові секвенційні форми числень Rn. L та Pr. L такі ж, як для Rn. GS та Pr. GS. Замкненість секвенції в численнях Rn. L та Pr. L задається умовою C CL. Числення QEq. L. Базові секвенційні форми такі ж, як для числення QL. Замкненість секвенції визначається умовою C CL CEq. T CEq T Un. D. Додаткові умови CEq. T та CEq T замкненості секвенції індуковані властивістю еквітонності (неокласична семантика) чи антитонності (пересичена семантика). CEq. T) існує пара формул |– та –| таких, що z X та y Y; CEq T) існує пара формул |– та –| таких, що z X та y Y Тут Х та Y – множини всіх означених та неозначених імен в даній вершині . Якщо виконується одна з умов CEq. T чи CEq T, то секвенцію назвемо – TХ–Y замкненою у випадку неокласичної семантики, та – FХ–Y замкненою у випадку пересиченої семантики. Якщо |– –| TХ–Y замкнена, то A, Х–Y |=T ; якщо |– –| FХ–Y замкнена, то A, Х–Y |=F . Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 25

Числення QR. Базові секвенційні форми такі ж, як і для числення QGS. Замкненість секвенції визначається умовою C CR Un. D. Умова СR така: СR) замкнена, якщо існує формула така, що –| та –| . Базові секвенційні форми числень Rn. R та Pr. R такі ж, як для Rn. GS та Pr. GS. Замкненість секвенції в численнях Rn. R та Pr. R задається умовою C CR. Числення QEq. R. Базові секвенційні форми такі ж, як для числення QR. Замкненість секвенції визначається умовою C CR CEq. F CEq F Un. D. Додаткові умови CEq. F та CEq F замкненості секвенції індуковані властивістю еквітонності (неокласич на семантика) чи нтитонності (пересичена семантика). а CEq. F) існує пара формул |– та –| таких, що z X та y Y; CEq F) існує пара формул |– та –| таких, що z X та y Y Тут Х та Y – множини всіх означених та неозначених імен в даній вершині . Якщо виконується одна з умов CEq. F чи CEq F, то секвенцію назвемо: – FХ–Y замкненою у випадку неокласичної семантики, – TХ–Y замкненою у випадку пересиченої семантики. Якщо |– –| FХ–Y замкнена, то A, Х–Y |=F ; якщо |– –| TХ–Y замкнена, то A, Х–Y |=T . Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 26

Числення QLR. Базові секвенційні форми такі ж, як і для числення QGS. Замкненість секвенції визначається умовою C CL & CR Un. D. Одночасне виконання СL та СR рівносильне виконанню умови: СLR) замкнена, якщо існують та : |– , –| . Базові секвенційні форми числень Rn. LR та Pr. LR такі ж, як для Rn. GS та Pr. GS. Замкненість секвенції в численнях Rn. LR та Pr. LR задається умовою С СLR. Числення QEq. LR. Базові секвенційні форми такі ж, як для числення QLR. Замкненість секвенції визначається умовою C (CL Eq. T CEq T) & (CR CEq. F CEq F) Un. D. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 27

Числення QCl. Замкненість секвенції дається умовою C Un. D. Базові секв. форми: | , |–RT, –|RT, |–RR, –|RR, |–R , –|R , |– N, |–R R, –|R R, |–R p, –|R p, |– , –| , |– R, –| R. Ці форми записуються згідно відповідних властивостей |=Cl (неокласична семантика) та |=Cm (пересичена семантика). Форми | та | мають традиційний вигляд: | | Форми | , |–RT, –|RT, |–RR, –|RR, |–R , –|R , |– N є базовими формами відомого реномінативного числення Rn. Cl. Базовими формами пропозиційного числення Pr. Cl є | , | , |. Замкненість секвенції в численнях Rn. Cl та Pr. Cl задається умовою С. Числення QEq. Cl. Базові секвенційні форми такі ж, як для числення QCl. Замкненість секвенції визначається умовою С. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 28

3. 2. Особливості побудови секвенційного дерева. Теорема коректності Поетапна процедура побудови сек. дерева для заданої секвенції фактично однакова для числень QGS, QL, QEq. L, QR, QEq. R, QLR, QEq. LR. Раніше описувались процедура побудови дерева для числення QCl, та подібна, але простіша процедура для неокласичного числення QEq. Cl. Ускладнення процедури побудови дерева в QGS, QL, QEq. L, QR, QEq. R, QLR, QEq. LR, QCl, зумовлене тим, що значення P(d) може бути різним залежно від того, входить чи не входить до d компонента з певним предметним іменем. Отже, при застосуванні F форм приклади можуть формуватися лише для означених імен, тому треба перебирати всі можливі розподіли наявних предм. імен на означені й неозначені. Це реалізуємо побудовою відп. розгалужень сек. дерева: якщо F форма застосовується вперше на етапі, нехай у вершині до формули вигляду –| x , –| |– x , |– то для будується не одна, а багато вершин "сестер", які є безпосередніми предками , мають одну й ту ж множину наявних імен і відрізняються лише різними множинами означених імен та множинами прикладів вигляду –| |– де у – означене. Теорема 1 (коректності). Нехай |– –| вивідна в численні певного класу. Тоді |=* для відп. відношення |=* у відп. семантиці Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 29

3. 3. Модельні множини Для доведення повноти збудованих секв. числень – метод модельних множин. Н – множина формул, специф. символами |– та –| , W nm(Н) – множина її означених імен, U = nm(Н) W – неозначених імен. Числення QGS. Н – GS модельна, якщо виконуються умови: НС) Не існує : |– Н та –| Н. НСU) Не існує |– Н та –| Н таких, що та мають однакові U неозначувані форми. НС та НСU – це умови коректності GS модельної множини. Н ) Якщо |– Н, то |– Н; якщо –| Н, то –| Н. Н ) Якщо |– Н, то |– Н або |– Н; якщо –| Н, то –| Н та –| Н. Н ) Якщо |– ( ) Н, то |– Н та |– Н; якщо –| ( ) Н, то –| Н або –| Н. НRT) Якщо |– Н, то |– Н; якщо –| Н, то –| Н. Н RT) Якщо |– Н, то |– Н; якщо –| Н, то –| Н. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 30

Н N) Якщо |– Н та у ( ), то |– Н; якщо –| Н та у ( ), то –| Н. Н N) Якщо |– Н та у ( ), то |– Н; якщо –| Н та у ( ), то –| Н. НRR) Якщо |– Н, то |– Н; якщо –| Н, то –| Н. Н RR) Якщо |– Н, то |– Н; якщо –| Н, то –| Н. НR ) Якщо |– Н, то |– Н; якщо –| Н, то –| Н. Н R ) Якщо |– Н, то |– Н; якщо –| Н, то –| Н. НR ) Якщо |– Н, то |– Н; якщо –| Н, то –| Н. Н R ) Якщо |– Н, то |– Н та |– Н; якщо –| Н, то –| Н або –| Н. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 31

НR R) Якщо |– Н, то |– Н; якщо –| Н, то –| Н. Н R R) Якщо |– Н, то |– Н; якщо –| Н, то –| Н. НR p) Якщо |– Н, то |– х Н; якщо –| Н, то –| х Н. Н R p) Якщо |– Н, то |– х Н; якщо –| Н, то –| х Н. Н ) Якщо |– х Н, то існує у W таке, що |– Н; якщо –| х Н, то –| Н для всіх у W. Н ) Якщо |– х Н, то |– Н для всіх у W; якщо –| х Н, то існує у W таке, що –| Н. Н R) Якщо |– Н, то існує у W таке, що |– Н; якщо –| Н, то –| Н для всіх у W. Н R) Якщо |– Н, то |– Н для всіх у W; якщо –| Н, то існує у W таке, що –| Н Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 32

Числення QL. Н – L модельна, якщо вик ся умови для GS мод. мн ни, а також: НСL) Не існує формули такої, що |– Н та |– Н. НС НСL та НСU – це умови коректності L мод. мн ни. Числення QEq. L. Н – Eq. L-модельна, якщо вона L-модельна та додатково – умови коректності: НCEq. T) Не існує пари ф л |– Н та –| Н: z W та y U; НCEq T) Не існує пари ф л |– Н та –| Н: z W та y U Числення QR. Н – R модельна, якщо вик ся умови для GS модельної мн ни, а також: НСR) Не існує формули такої, що –| Н та –| Н. НС, НСR та НСU – умови коректності R мод. мн ни. Числення QEq. R. Н – Eq. R-модельна, якщо R-модельна та маємо додаткові умови коректності: НCEq. F) Не існує |– Н та –| Н таких: z W та y U; НCEq F) Не існує |– Н та –| Н таких: z W та y U Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 33

Числення QLR. Н – LR модельна, якщо вик ся умови GS мод. мн ни, та умови: НСLR) Не існують формули такі, що |– Н, |– Н та –| Н, –| Н. НС, НСLR та НСU – умови коректності LR мод. мн ни. Числення QEq. LR. Н – Eq. LR-модельна, якщо вик ся умови GS мод. мн ни, а також НСL, НCEq. T, НCEq T або НСR, НCEq. F, НCEq F. Числення QCl. Н – C-модельна, якщо виконуються НС, НСU, Н , НRT, Н N, НRR, НR R, НR p, Н R, а також: Н ) Якщо |– Н, то –| Н; якщо –| Н, то |– Н. НС та НСU – умови коректності C мод. мн ни. Числення QEq. Cl. Множина Н – Eq. C-модельна, якщо виконуються НС, Н , НRT, Н N, НRR, НR R, НR p, Н R. НС – умова коректності Eq. C модельної можини. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 34

4. ПОВНОТА СЕКВЕНЦІЙНИХ ЧИСЛЕНЬ Незамкнений шлях в секвенційному дереві індукує модельну множину. Теорема 2. Нехай – незамкнений шлях у сек. дереві, Н – множина всіх специф. формул секвенцій цього шляху. Тоді Н – модельна множина відповідного типу (GS , L , Eq. L , R , Eq. R , LR , Eq. LR , C модельна). За модельною множиною можна побудувати контрмодель. Теорема 3. Нехай Н – модельна множина, яка може бути GS , L , Eq. L , R , Eq. R , LR , Eq. LR модельною. Тоді існують моделі мови A = (A, I), B = (A, I) та , VA: 1) |– Н T( A) та –| Н T( A); 2) |– Н F( B) та –| Н F( B). Такі пари (A, ) та (B, ) – T контрмодель та F контрмодель. Теорема 4. Нехай Н – C модельна множина. Тоді існують моделі мови A = (A, I), B = (A, I) та , VA такі: 1) |– Н T( A) та –| Н F( A); 2) |– Н F( B) та –| Н T( B). Такі пари (A, ) та (B, ) – Cl контрмодель та Cm контрмодель. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 35

Теорема повноти для різних варіантів секвенційних числень та логічних наслідків формулюється однаково. Поєднаємо теореми повноти та теореми коректності: Теорема 5. 1) |=Cl в неоклас. сем ці |– –| вивідна в QCl; 2) |=Cm в пересич. сем ці |– –| вивідна в QCl; 3) |=Cl в неоклас. сем ці ЛЕП |– –| вивідна в QEq. CL; 4) |=Cm в пересич. сем ці ЛАП |– –| вивідна в QEq. CL; 5) |=T в неоклас. сем ці |– –| вивідна в QL; 6) |=F в пересич. сем ці |– –| вивідна в QL; 7) |=T в неоклас. сем ці ЛЕП |– –| вивідна в QEq. L; 8) |=F в пересич. сем ці ЛАП |– –| вивідна в QEq. L; 9) |=F в неоклас. сем ці |– –| вивідна в QR; 10) |=T в пересич. сем ці |– –| вивідна в QR; 11) |=F в неоклас. сем ці ЛЕП |– –| вивідна в QEq. R; 12) |=T в пересич. сем ці ЛАП |– –| вивідна в і QEq. R; 13) |=TF в неоклас. чи пересич. сем ці |– –| вивідна в QLR; 14) |=TF в неоклас. сем ці ЛЕП чи пересич. сем ці ЛАП |– –| вивідна в QEq. LR; 15) |=TF в загальній сем ці |– –| вивідна в QGS Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 36

ВИСНОВКИ Використання КНП дає змогу побудувати широкий спектр логічних форма лізмів різного рівня абстрактності та загальності на єдиній з програмуванням методологічній основі. В доповіді досліджено чисті першопорядкові КНЛ логік часткових однозначних, тотальних неоднозначних та часткових неоднозначних квазіарних предикатів, для них побудовано числення секвенційного типу. 1. Для чистих першопорядкових КНЛ часткових однозначних, тотальних неоднозначних та часткових неоднозначних квазіарних предикатів запропоновано різні семантики та різні формалізації відношення логічного наслідку. Досліджено властивості цих відношень, визначено співвідношення між різними наслідками в різних семантиках. 2. Для зазначених КНЛ побудовано числення секвенційного типу. Основою такої побудови є властивості відношень логічного наслідку для множин формул. 3. Розмаїття цих відношень дає низку різновидностей секвенційних числень. Такі числення збудовано як для загального випадку логік квазіарних предикатів, так і для логік однозначних еквітонних та тотальних антитонних предикатів. 4. Для пропонованих числень наведено базові секвенційні форми та умови замкненості секвенцій, визначено поняття модельної множини. Для побудованих числень доведено теореми коректності та повноти. Укр. ПРОГ’ 2012 23 -24 травня, 2012, Київ, Україна 37