Скачать презентацию SEISMIC SOURCES SEISMIC SOURCES Solution for the Скачать презентацию SEISMIC SOURCES SEISMIC SOURCES Solution for the

b4719fd17bd3702fa60805c74ef0be8b.ppt

  • Количество слайдов: 102

SEISMIC SOURCES SEISMIC SOURCES

SEISMIC SOURCES Solution for the displacement potential Properties of the disp potential 1. An SEISMIC SOURCES Solution for the displacement potential Properties of the disp potential 1. An outgoing D’Alembert solution in the spherical coordinate. 2. Functional shape is the same as the force-time history. Displacement field Near-field term Far-field term

8. 3 Elastostatics • Purpose – to determine the static displacement u in an 8. 3 Elastostatics • Purpose – to determine the static displacement u in an isotropic, infinite, homogeneous elastic medium due to a point source at point O. O F

8. 3 Elastostatics Three-dimensional delta function (in spherical polar coordinate): With the use of 8. 3 Elastostatics Three-dimensional delta function (in spherical polar coordinate): With the use of Gauss’ theorem:

8. 3. 1 Static displacement field due to a single force • Elastic equation 8. 3. 1 Static displacement field due to a single force • Elastic equation without time-dependent displacement term (utt=0) • The point force is balanced by the stresses/strain • Consider a point force of magnitude F at the origin

8. 3. 1 Static displacement field due to a single force The equation of 8. 3. 1 Static displacement field due to a single force The equation of equilibrium becomes: Note that the representations of force and displacement field are similar! The solution form (Helmholtz’s theorem):

8. 3. 1 Static displacement field due to a single force Which can be 8. 3. 1 Static displacement field due to a single force Which can be satisfied by having:

8. 3. 1 Static displacement field due to a single force If we put 8. 3. 1 Static displacement field due to a single force If we put Ap=Apa and As=Asa, we obtain two Poisson’s equations: The solutions (of potentials) are

8. 3. 1 Static displacement field due to a single force Plugging in the 8. 3. 1 Static displacement field due to a single force Plugging in the potentials Ap and As and expressing the vector operations with indicial notation, and yield the ith component of displacement for a unit force (F=1) in the jth direction, uij:

8. 3. 1 Static displacement field due to a single force Somigliana tensor Symmetry: 8. 3. 1 Static displacement field due to a single force Somigliana tensor Symmetry: uij= u ji

8. 3. 1 Static displacement field due to a single force Thanks to the 8. 3. 1 Static displacement field due to a single force Thanks to the symmetry, there are only 6 independent permutations:

8. 3. 1 Static displacement field due to a single force Find the displacements 8. 3. 1 Static displacement field due to a single force Find the displacements given in polar coordinates due to a point force applied in the x 1 direction (Figure 8. 12), using the Jacobian coordinate transformation matrix (8. 19)

8. 3. 1 Static displacement field due to a single force (typo in textbook!) 8. 3. 1 Static displacement field due to a single force (typo in textbook!) In the x 1 x 3 plane, φ=0: The (x 1 x 3 plane) static radial deformation and shear deformation due to a single force (Fig 8. 12)

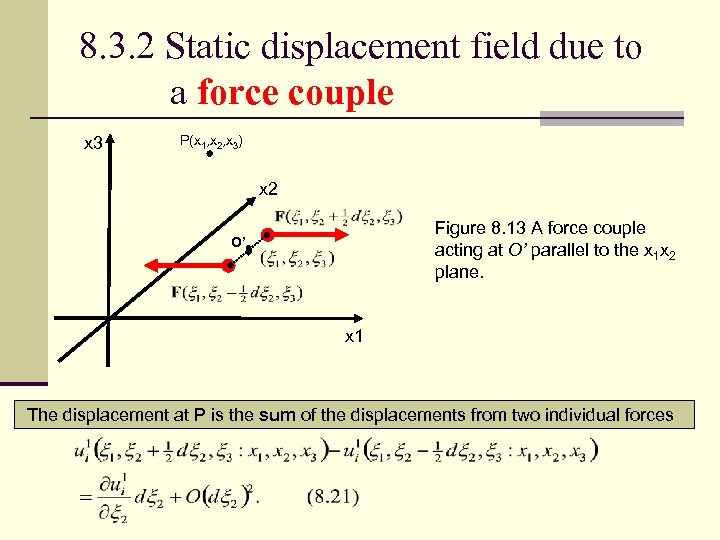8. 3. 2 Static displacement field due to a force couple x 3 P(x 8. 3. 2 Static displacement field due to a force couple x 3 P(x 1, x 2, x 3) x 2 Figure 8. 13 A force couple acting at O’ parallel to the x 1 x 2 plane. O’ x 1 The displacement at P is the sum of the displacements from two individual forces

8. 3. 2 Static displacement field due to a force couple The displacement due 8. 3. 2 Static displacement field due to a force couple The displacement due to the force couple is given by:

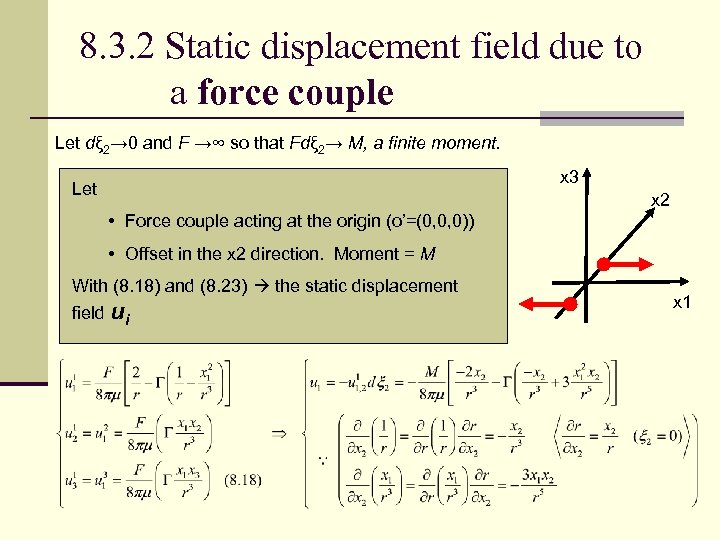8. 3. 2 Static displacement field due to a force couple Let dξ 2→ 8. 3. 2 Static displacement field due to a force couple Let dξ 2→ 0 and F →∞ so that Fdξ 2→ M, a finite moment. x 3 Let x 2 • Force couple acting at the origin (o’=(0, 0, 0)) • Offset in the x 2 direction. Moment = M With (8. 18) and (8. 23) the static displacement field ui x 1

8. 3. 2 Static displacement field due to a force couple In the same 8. 3. 2 Static displacement field due to a force couple In the same way, we may derive u 2 and u 3 for the single couple

8. 3. 2 Static displacement field due to a force couple Similarly, for single 8. 3. 2 Static displacement field due to a force couple Similarly, for single couple oriented along the x 2 axis with offset arm along the x 1 direction x 3 x 2 x 1 In general j : direction of force k : direction of offset arm

8. 3. 3 Static displacement field due to a double couple Principles of superposition: 8. 3. 3 Static displacement field due to a double couple Principles of superposition: x 3 x 2 The displacement is the sum of the displacements from two individual couples (+/- of M) x 1 A double couple in the x 1 x 2 plane

8. 3. 3 Static displacement field due to a double couple Convert to spherical 8. 3. 3 Static displacement field due to a double couple Convert to spherical polar coordinates with (8. 19) Static deformations decay rapidly. On the x 1 x 2 plane, θ=π/2, uθ=0, and

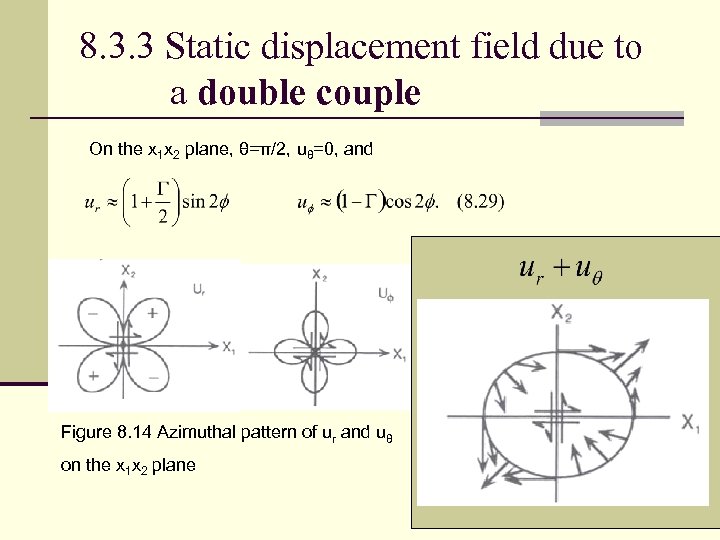8. 3. 3 Static displacement field due to a double couple On the x 8. 3. 3 Static displacement field due to a double couple On the x 1 x 2 plane, θ=π/2, uθ=0, and Figure 8. 14 Azimuthal pattern of ur and uθ on the x 1 x 2 plane

8. 3. 3 Static displacement field due to a double couple n The displacement 8. 3. 3 Static displacement field due to a double couple n The displacement field due to a shear dislocation can be given by the displacement field due to a distribution of equivalent double couples that are placed in a medium without any dislocation. n Since static deformations decay rapidly with distance from the source, ground deformations are usually near the fault a point-source approximation is never valid finite fault numerically discretized distribution of double couples.

Going beyond the simple faulting model in geodetic modeling n Incorporating viscoelastic effects of Going beyond the simple faulting model in geodetic modeling n Incorporating viscoelastic effects of the deeper crust. n Adding layering and elastic parameter heterogeneity in the Earth model. n Variable slip function or changing fault mechanism. n Curved fault plane

8. 4 Elastodynamics Elastodynamic equations: Consider a time-dependent body force: Following the same basic 8. 4 Elastodynamics Elastodynamic equations: Consider a time-dependent body force: Following the same basic procedure as used in elastostatic problem.

8. 4 Elastodynamics Again, we seek a solution of the form: Compare it to 8. 4 Elastodynamics Again, we seek a solution of the form: Compare it to (8. 14)

8. 4 Elastodynamics Putting Ap=Apa. As=Asa, we obtain twos scalar equations: 8. 4 Elastodynamics Putting Ap=Apa. As=Asa, we obtain twos scalar equations:

8. 4 Elastodynamics: The solution to an inhomogeneous wave equation An inhomogeneous wave equation: 8. 4 Elastodynamics: The solution to an inhomogeneous wave equation An inhomogeneous wave equation: Where g is a “point” source both in space and time: The solution is: (Buy it, for now) (Box 2. 5)

8. 4 Elastodynamics Standard type of D’Alembert-type solution: For a point force at x=(ξ 8. 4 Elastodynamics Standard type of D’Alembert-type solution: For a point force at x=(ξ 1, ξ 2, ξ 3) applied at t=τ. For a time-dependent point force f(t) applied at x=(ξ 1, ξ 2, ξ 3)

8. 4 Elastodynamics If the source is extended through a volume V, as well 8. 4 Elastodynamics If the source is extended through a volume V, as well as in time

8. 4 Elastodynamics The solutions to (8. 33) 8. 4 Elastodynamics The solutions to (8. 33)

So far, so good ? Sorry, it’s getting messy … So far, so good ? Sorry, it’s getting messy …

8. 4 Elastodynamics How to deal with this integration ? Integrating over V via 8. 4 Elastodynamics How to deal with this integration ? Integrating over V via the system of concentric spherical shells …

8. 4 Elastodynamics 8. 4 Elastodynamics

8. 4 Elastodynamics 8. 4 Elastodynamics

8. 4 Elastodynamics 8. 4 Elastodynamics

8. 4 Elastodynamics Typo in textbook! 8. 4 Elastodynamics Typo in textbook!

8. 4 Elastodynamics Stokes solution (for point force in the j direction, located at 8. 4 Elastodynamics Stokes solution (for point force in the j direction, located at the origin): • Near-field term Far-field term

8. 4 Elastodynamics Properties of the far-field P-wave 1. It attenuates as 1/r 2. 8. 4 Elastodynamics Properties of the far-field P-wave 1. It attenuates as 1/r 2. Arrival time=r/αwith velocity α 3. waveform is proportional to the applied force at the retarded time. 4. The displacement is parallel to the direction from the source (up×γ=0) (longitudinal wave) 5. |up| is proportional to γj

Properties of the far-field P-wave 4. The displacement is parallel to the direction from Properties of the far-field P-wave 4. The displacement is parallel to the direction from the source (up×γ=0) (longitudinal wave) 5. |up| is proportional to γj

8. 4 Elastodynamics Properties of the far-field S-wave 1. It attenuates as 1/r 2. 8. 4 Elastodynamics Properties of the far-field S-wave 1. It attenuates as 1/r 2. Arrival time=r/β with velocityβ 3. waveform is proportional to the applied force at the retarded time. 4. The displacement is perpendicular to the direction from the source (us ．γ=0) (transverse wave)

8. 4 Elastodynamics n The displacement field for single couples and double couples can 8. 4 Elastodynamics n The displacement field for single couples and double couples can be obtained by differentiating the single-force results w. r. t appropriate coordinates. (The same as we did for the static fields. ) n Only far-field displacements are discussed from now on.

8. 4 Elastodynamics – The displacement field due to a single couple F F 8. 4 Elastodynamics – The displacement field due to a single couple F F 2

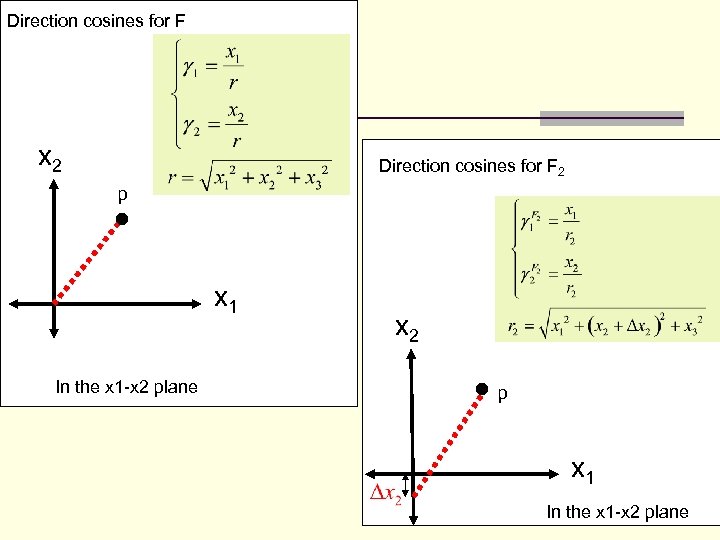Direction cosines for F x 2 Direction cosines for F 2 p x 1 Direction cosines for F x 2 Direction cosines for F 2 p x 1 In the x 1 -x 2 plane x 2 p x 1 In the x 1 -x 2 plane

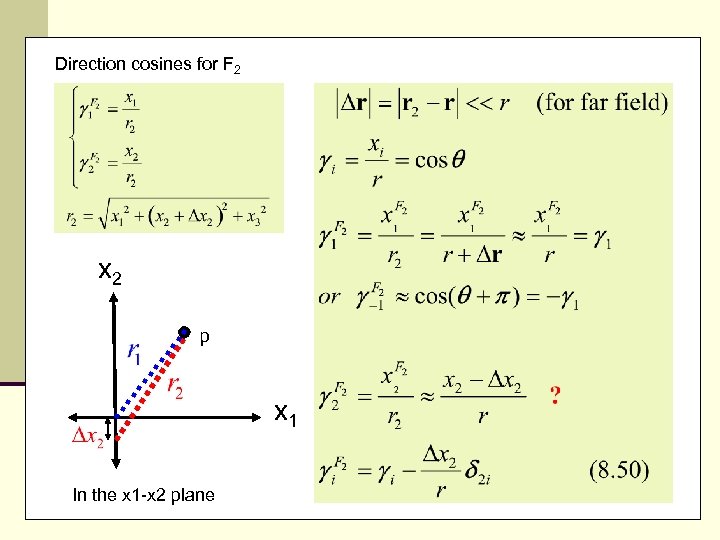Direction cosines for F 2 x 2 p x 1 In the x 1 Direction cosines for F 2 x 2 p x 1 In the x 1 -x 2 plane

8. 4 Elastodynamics – The displacement field due to a single couple For Expand 8. 4 Elastodynamics – The displacement field due to a single couple For Expand this term around (t-r 2/α) in Taylor series. • Temporal differentiation of the source time history

8. 4 Elastodynamics – The displacement field due to a single couple • Temporal 8. 4 Elastodynamics – The displacement field due to a single couple • Temporal differentiation of the source time history

8. 4 Elastodynamics – The displacement field due to a single couple Near-field terms 8. 4 Elastodynamics – The displacement field due to a single couple Near-field terms (Decays as 1/r 2) Far-field displacement (Decays as 1/r) The far-field displacement is sensitive to particle velocity at the source rather than to particle displacements. (rev: Eq 8. 3)

8. 4 Elastodynamics – The displacement field due to a single couple Introduce the 8. 4 Elastodynamics – The displacement field due to a single couple Introduce the moment representation: M

8. 4 Elastodynamics – The displacement field due to a single couple/double couple Solution 8. 4 Elastodynamics – The displacement field due to a single couple/double couple Solution for the single couple is x 2 x 1 Δx 2 Symmetry in force direction and offset direction x 2 Solution to a double couple x 1 x 3 x 2 Δx 1 A double couple in the x 1 x 2 plane

Elastodynamic Green function Gij : elastodynamic Green function – The displacement field from the Elastodynamic Green function Gij : elastodynamic Green function – The displacement field from the simplest source – namely, the unidirectional unit impulse, which is localized precisely in both space and time Notaion – Gij : ith response to impulse force acting on jth direction.

8. 4 Elastodynamics – general form of the far-field displacement for a couple Using 8. 4 Elastodynamics – general form of the far-field displacement for a couple Using the notation of Green function, the general form of the far-field displacement field (P and S) for a couple in the pq plane is given by P S Mpq : seismic moment tensor (9 couples/dipoles)

8. 4 Elastodynamics – Radiation pattern of the far-field displacement for double couple Convert 8. 4 Elastodynamics – Radiation pattern of the far-field displacement for double couple Convert to spherical coordinate system (for p=1, q=3) Time-dependent moment function The far-field displacements are proportional to the moment rate function.

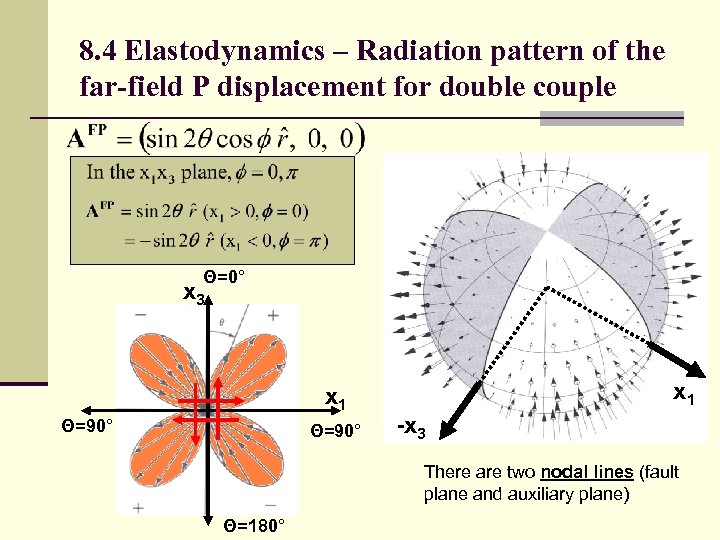8. 4 Elastodynamics – Radiation pattern of the far-field P displacement for double couple 8. 4 Elastodynamics – Radiation pattern of the far-field P displacement for double couple Θ=0° x 3 x 1 Θ=90° x 1 -x 3 There are two nodal lines (fault plane and auxiliary plane) Θ=180°

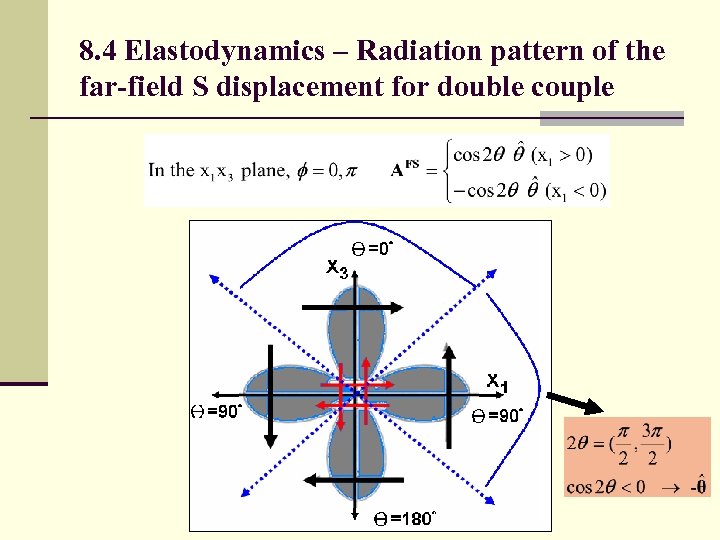
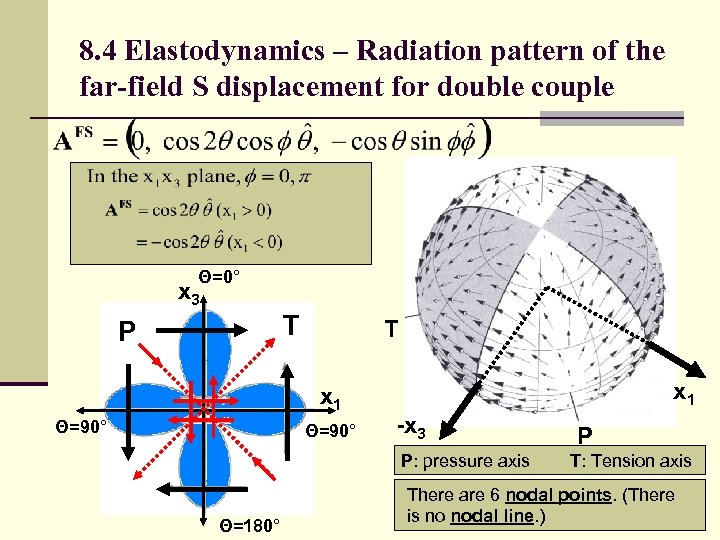8. 4 Elastodynamics – Radiation pattern of the far-field S displacement for double couple 8. 4 Elastodynamics – Radiation pattern of the far-field S displacement for double couple Θ=0° x 3 T P T x 1 Θ=90° x 1 -x 3 P: pressure axis Θ=180° P T: Tension axis There are 6 nodal points. (There is no nodal line. )

8. 4 Elastodynamics – Radiation pattern of the far-field S displacement for double couple 8. 4 Elastodynamics – Radiation pattern of the far-field S displacement for double couple

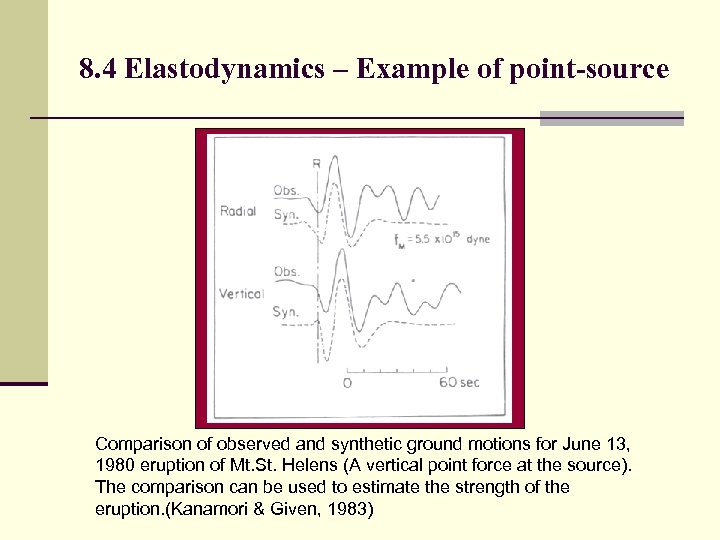8. 4 Elastodynamics – Example of point-source Comparison of observed and synthetic ground motions 8. 4 Elastodynamics – Example of point-source Comparison of observed and synthetic ground motions for June 13, 1980 eruption of Mt. St. Helens (A vertical point force at the source). The comparison can be used to estimate the strength of the eruption. (Kanamori & Given, 1983)

8. 4 Elastodynamics – Example of point-source Observed Double couple Single force Observed and 8. 4 Elastodynamics – Example of point-source Observed Double couple Single force Observed and interpretations of the source mechanism for the 1975 Kalapana, Hawaii event. (Eissler and Kanamori, 1987)

8. 4 Elastodynamics – the nature of moment rate function – step/delta function Step 8. 4 Elastodynamics – the nature of moment rate function – step/delta function Step function M(t) t ● M(t) δ function t

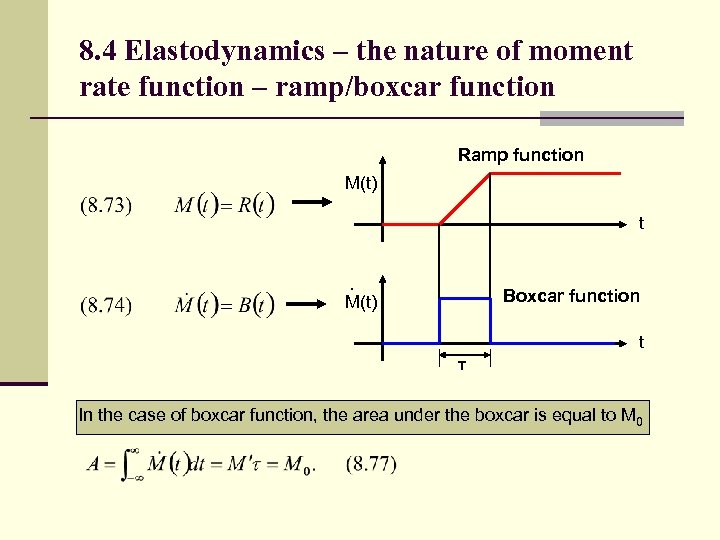8. 4 Elastodynamics – the nature of moment rate function – ramp/boxcar function Ramp 8. 4 Elastodynamics – the nature of moment rate function – ramp/boxcar function Ramp function M(t) t ● Boxcar function M(t) t τ In the case of boxcar function, the area under the boxcar is equal to M 0

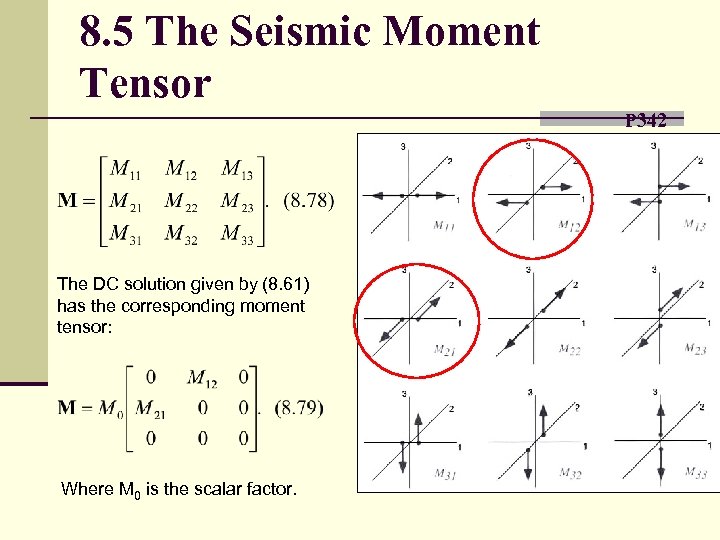8. 5 The Seismic Moment Tensor P 342 The DC solution given by (8. 8. 5 The Seismic Moment Tensor P 342 The DC solution given by (8. 61) has the corresponding moment tensor: Where M 0 is the scalar factor.

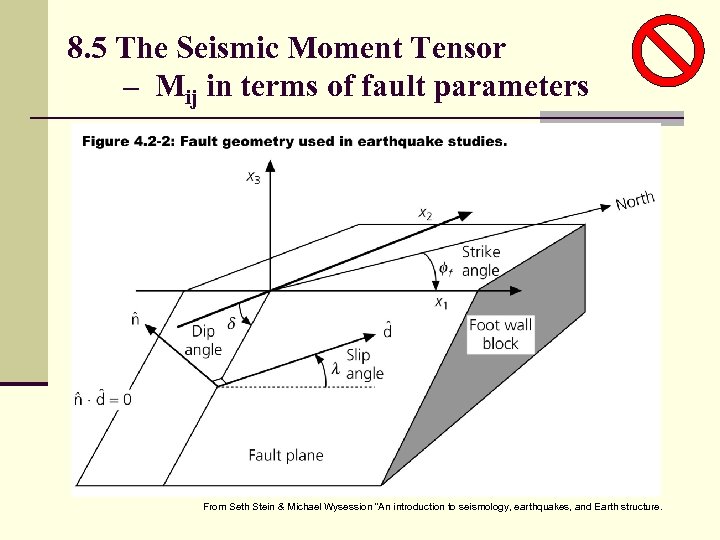8. 5 The Seismic Moment Tensor – Mij in terms of fault parameters From 8. 5 The Seismic Moment Tensor – Mij in terms of fault parameters From Seth Stein & Michael Wysession “An introduction to seismology, earthquakes, and Earth structure.

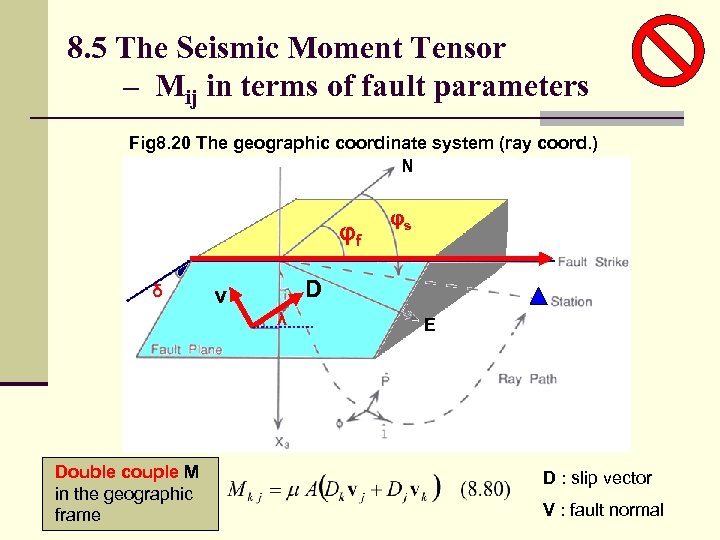8. 5 The Seismic Moment Tensor – Mij in terms of fault parameters Fig 8. 5 The Seismic Moment Tensor – Mij in terms of fault parameters Fig 8. 20 The geographic coordinate system (ray coord. ) N φf δ D v λ Double couple M in the geographic frame φs E D : slip vector V : fault normal

8. 5 The Seismic Moment Tensor – Mij in terms of fault parameters Double 8. 5 The Seismic Moment Tensor – Mij in terms of fault parameters Double couple Express D and v in terms of fault parameters (φf, δ, λ)

8. 5 The Seismic Moment Tensor – double couple Mij in terms of fault 8. 5 The Seismic Moment Tensor – double couple Mij in terms of fault parameters In the same way:

8. 5 The Seismic Moment Tensor – moment weighted Green’s function It’s possible to 8. 5 The Seismic Moment Tensor – moment weighted Green’s function It’s possible to construct the P or S motion for a moment tensor by summing the moment weighted Green’s function The basis for many synthetic seismogram programs and waveform inversions.

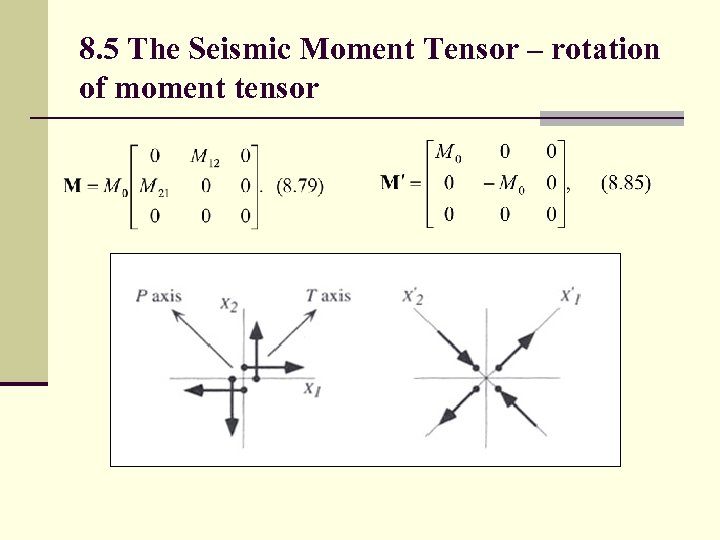8. 5 The Seismic Moment Tensor – rotation of moment tensor 8. 5 The Seismic Moment Tensor – rotation of moment tensor

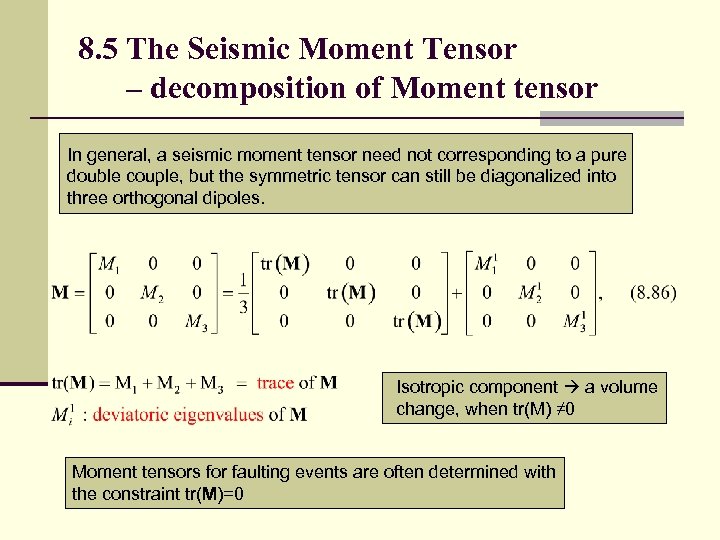8. 5 The Seismic Moment Tensor – decomposition of Moment tensor In general, a 8. 5 The Seismic Moment Tensor – decomposition of Moment tensor In general, a seismic moment tensor need not corresponding to a pure double couple, but the symmetric tensor can still be diagonalized into three orthogonal dipoles. Isotropic component a volume change, when tr(M) ≠ 0 Moment tensors for faulting events are often determined with the constraint tr(M)=0

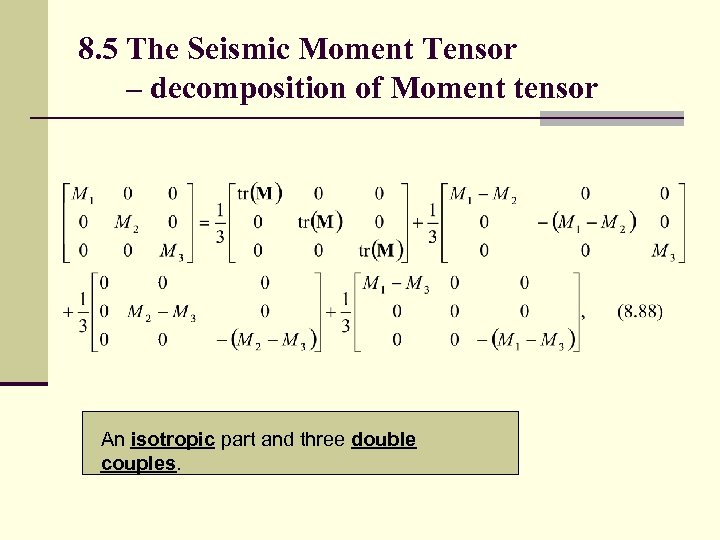8. 5 The Seismic Moment Tensor – decomposition of Moment tensor An isotropic part 8. 5 The Seismic Moment Tensor – decomposition of Moment tensor An isotropic part and three double couples.

8. 5 The Seismic Moment Tensor – decomposition of Moment tensor CLVD: componsated linear 8. 5 The Seismic Moment Tensor – decomposition of Moment tensor CLVD: componsated linear vector dipoles An isotropic part and three CLVDs

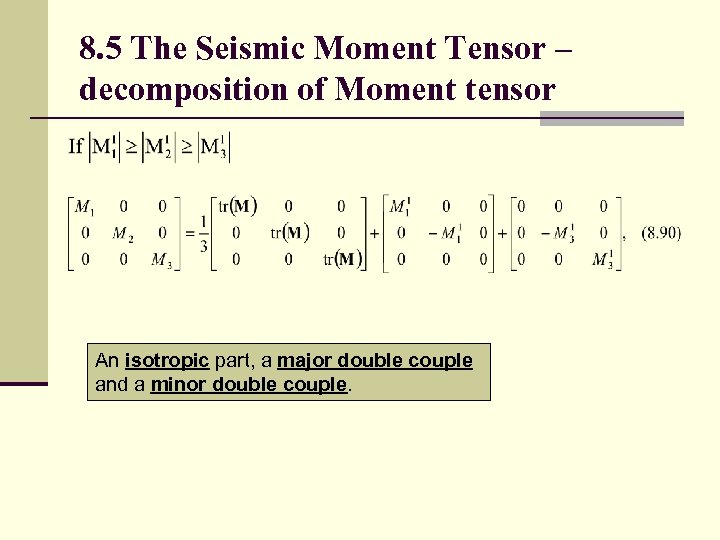8. 5 The Seismic Moment Tensor – decomposition of Moment tensor An isotropic part, 8. 5 The Seismic Moment Tensor – decomposition of Moment tensor An isotropic part, a major double couple and a minor double couple.

8. 5 The Seismic Moment Tensor – decomposition of Moment tensor Where ε is 8. 5 The Seismic Moment Tensor – decomposition of Moment tensor Where ε is a measure of the size of the CLVD component relative to the double couple. For a pure double couple, ε=0.

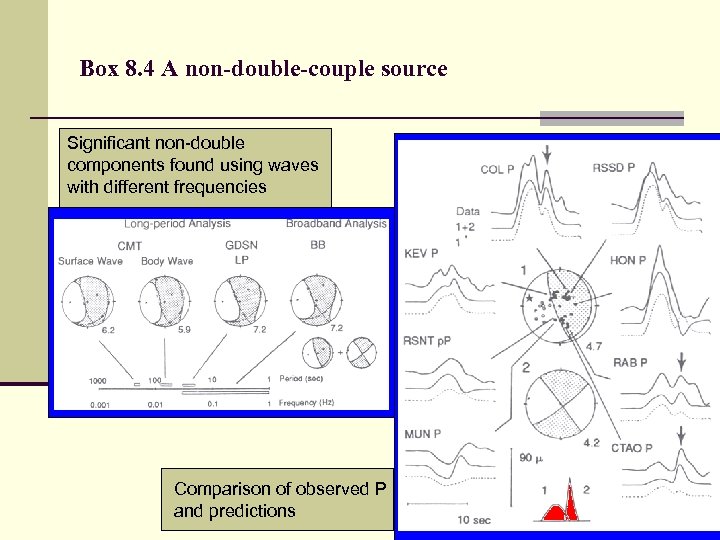Box 8. 4 A non-double-couple source Significant non-double components found using waves with different Box 8. 4 A non-double-couple source Significant non-double components found using waves with different frequencies Comparison of observed P and predictions

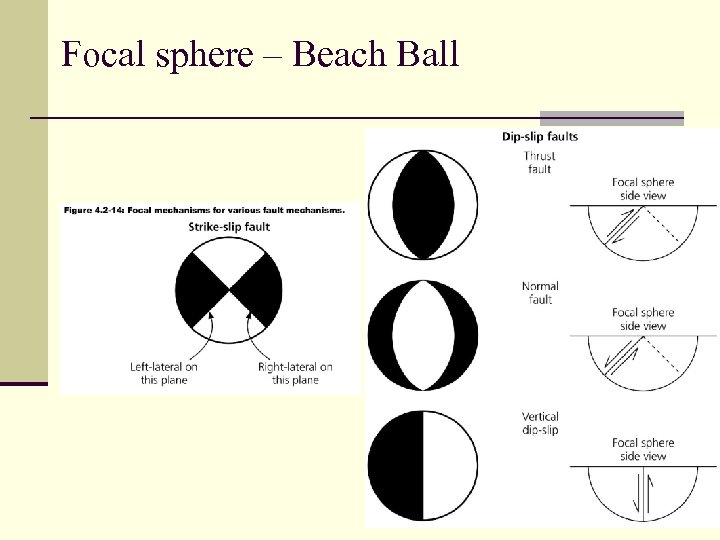Focal sphere – Beach Ball Focal sphere – Beach Ball

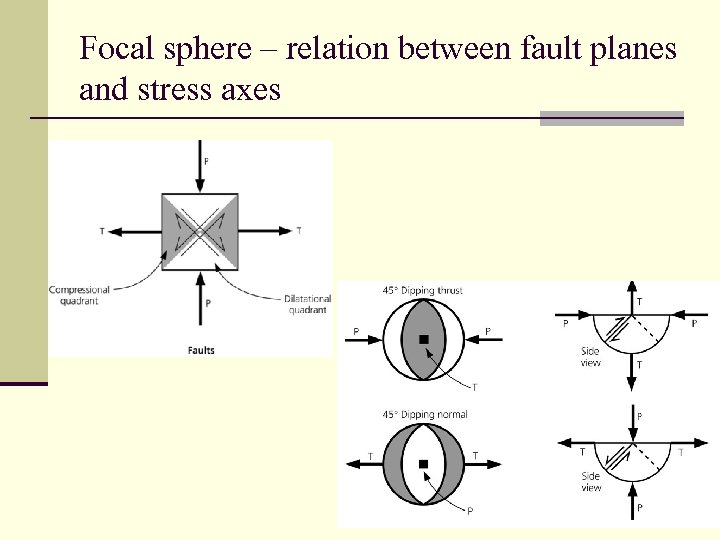Focal sphere – relation between fault planes and stress axes Focal sphere – relation between fault planes and stress axes

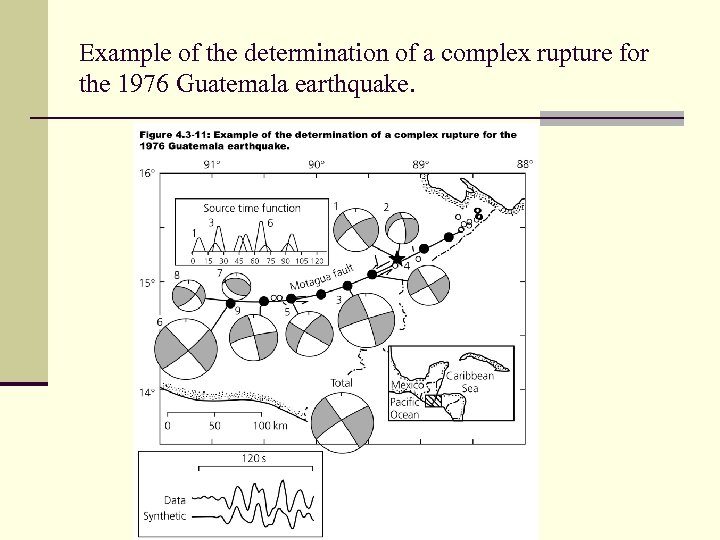Example of the determination of a complex rupture for the 1976 Guatemala earthquake. Example of the determination of a complex rupture for the 1976 Guatemala earthquake.

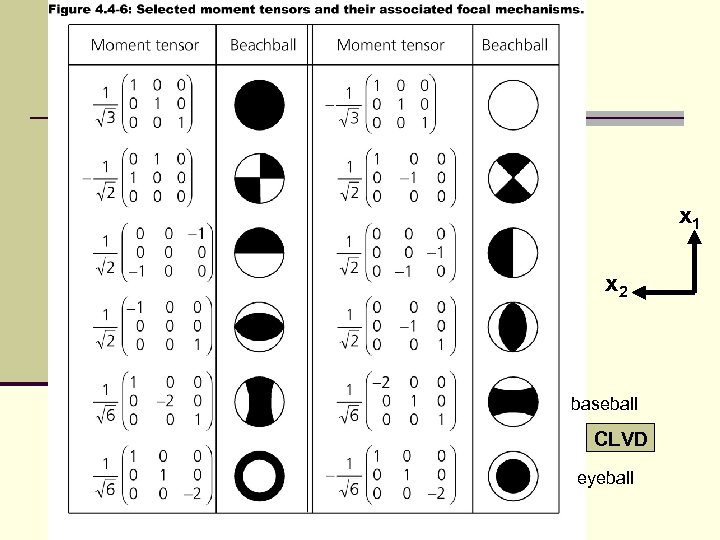x 1 x 2 baseball CLVD eyeball x 1 x 2 baseball CLVD eyeball

The END The END

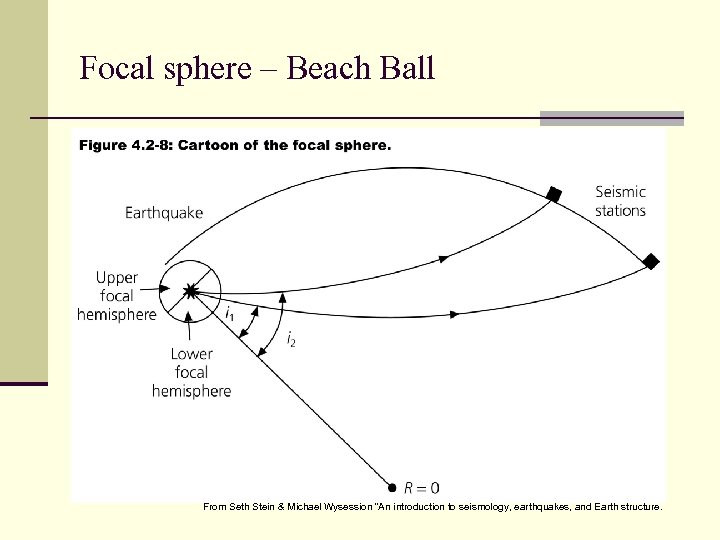Focal sphere – Beach Ball From Seth Stein & Michael Wysession “An introduction to Focal sphere – Beach Ball From Seth Stein & Michael Wysession “An introduction to seismology, earthquakes, and Earth structure.

Focal sphere – Beach Ball From Seth Stein & Michael Wysession “An introduction to Focal sphere – Beach Ball From Seth Stein & Michael Wysession “An introduction to seismology, earthquakes, and Earth structure.

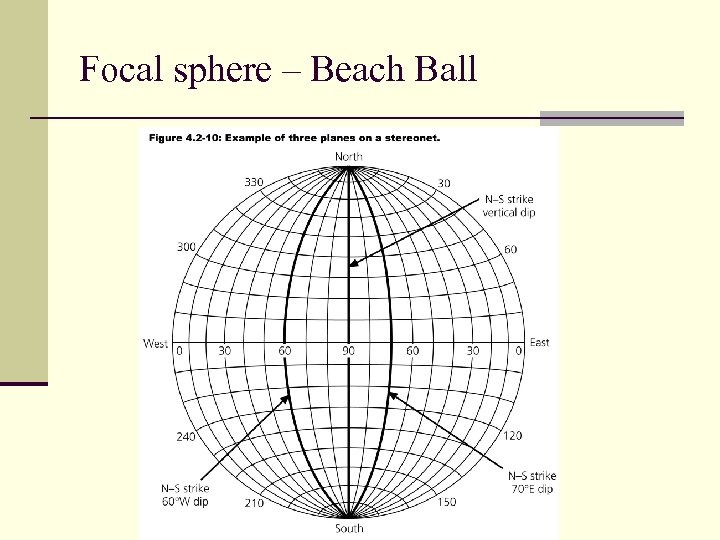Focal sphere – Beach Ball Focal sphere – Beach Ball

Focal sphere – Beach Ball Focal sphere – Beach Ball

8. 4 Elastodynamics For p. 334 8. 4 Elastodynamics For p. 334

8. 4 Elastodynamics p. 335 8. 4 Elastodynamics p. 335

8. 4 Elastodynamics p. 335 -336 8. 4 Elastodynamics p. 335 -336

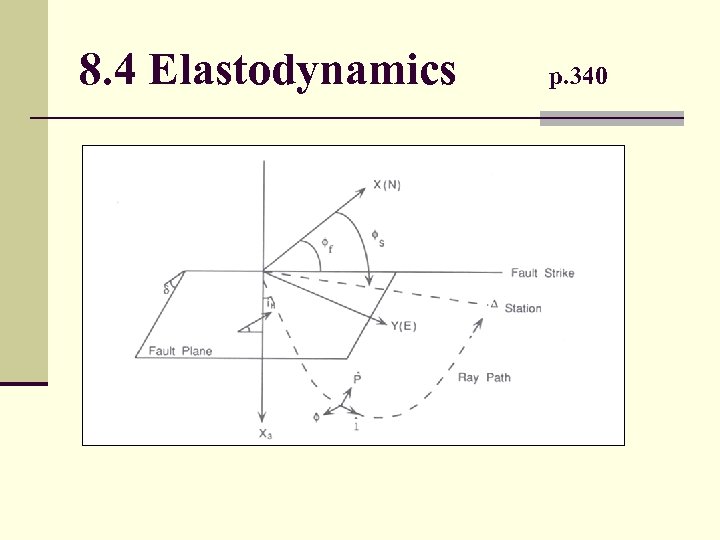8. 4 Elastodynamics p. 340 8. 4 Elastodynamics p. 340

8. 4 Elastodynamics p. 339 -340 8. 4 Elastodynamics p. 339 -340

8. 4 Elastodynamics p. 340 -341 8. 4 Elastodynamics p. 340 -341

8. 4 Elastodynamics p. 341 8. 4 Elastodynamics p. 341

8. 6 Determination of Faulting Orientation P 347 8. 6 Determination of Faulting Orientation P 347

8. 6 Determination of Faulting Orientation P 347 8. 6 Determination of Faulting Orientation P 347

8. 6 Determination of Faulting Orientation P 348 8. 6 Determination of Faulting Orientation P 348

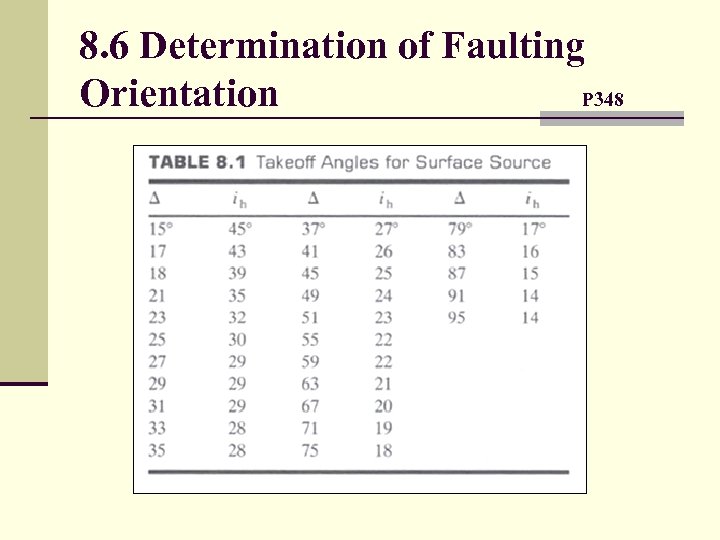8. 6 Determination of Faulting Orientation P 348 8. 6 Determination of Faulting Orientation P 348

8. 6 Determination of Faulting Orientation P 349 1. 2. 3. 4. 8. 6 Determination of Faulting Orientation P 349 1. 2. 3. 4.

8. 6 Determination of Faulting Orientation P 350 8. 6 Determination of Faulting Orientation P 350

8. 6 Determination of Faulting Orientation P 351 8. 6 Determination of Faulting Orientation P 351

8. 6 Determination of Faulting Orientation P 350 -351 8. 6 Determination of Faulting Orientation P 350 -351

8. 6 Determination of Faulting Orientation P 352 8. 6 Determination of Faulting Orientation P 352

8. 6 Determination of Faulting Orientation P 352 8. 6 Determination of Faulting Orientation P 352

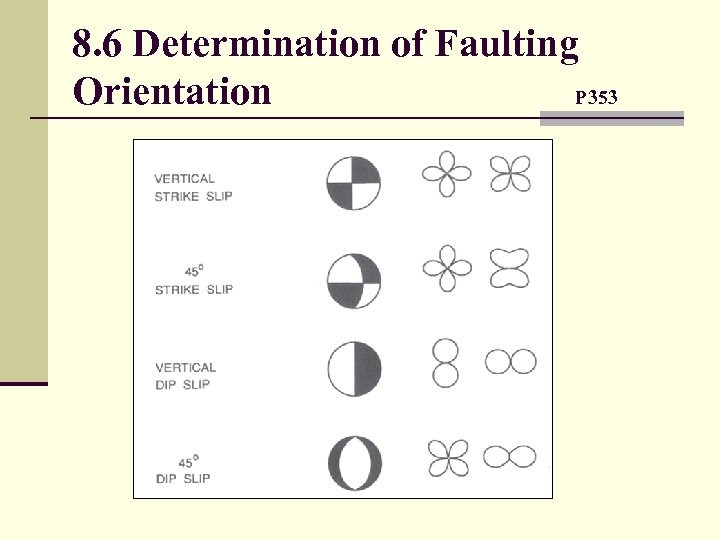8. 6 Determination of Faulting Orientation P 353 8. 6 Determination of Faulting Orientation P 353

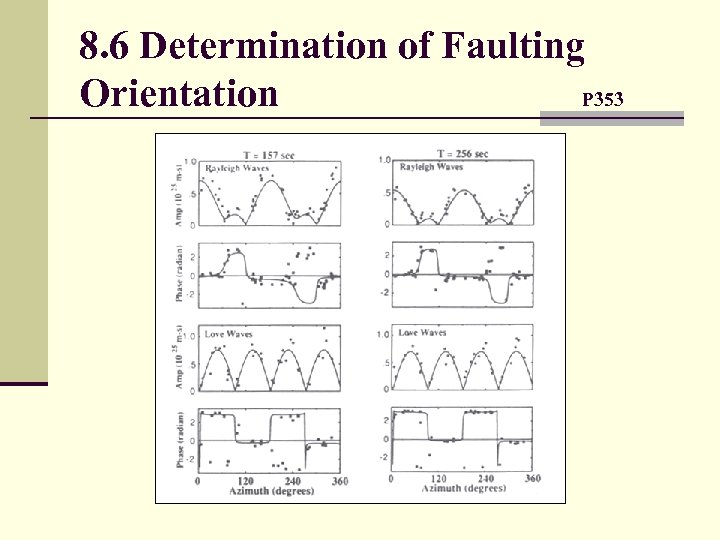8. 6 Determination of Faulting Orientation P 353 8. 6 Determination of Faulting Orientation P 353

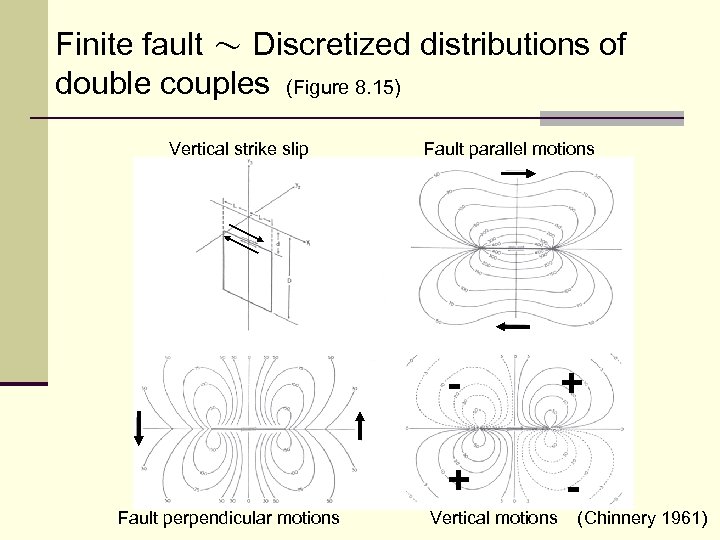Finite fault ～ Discretized distributions of double couples (Figure 8. 15) Vertical strike slip Finite fault ～ Discretized distributions of double couples (Figure 8. 15) Vertical strike slip Fault parallel motions + Fault perpendicular motions + - Vertical motions (Chinnery 1961)