Сегодня Wednesday February 14 2018 МЕХАНИКА Сегодня

Сегодня: Wednesday, February 14, 2018 МЕХАНИКА

Сегодня: Wednesday, February 14, 2018 ТЕМА: КИНЕМАТИКА Содержание лекции: 1. 1. Введение 1. 2. Векторные величины 1. 3. Кинематика поступательного движения материальной точки 1. 4. Мгновенная скорость, ускорение 1. 5. Кинематика вращательного движения

Введение. Модели в механике Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.

Введение. Модели в механике Кинематика изучает движение тел, не рассматривая причин, которые это движение вызывают. Она использует понятия: траектория, путь, перемещение, время, скорость и ускорение.

2. 1. Модели в механике Динамика - изучает законы движения тел и причины, которые вызывают или изменяют это движение. Она наряду с кинематическими, использует понятия: масса, сила, импульс, энергия.

Введение. Модели в механике Пытаясь понять и объяснить определенный класс явлений, ученые часто прибегают к использованию модели. При этом под моделью понимают некоторый мысленный образ явления, опирающийся на уже известные понятия и позволяющий построить полезную аналогию.

Введение. Модели кинематики Материальной точкой (частицей) называют тело в тех случаях, когда изучают его поступательное движение как целого. При этом полагают, что его размеры, форма и другие структурные свойства, а также протекающие в нем процессы, не влияют на движение тела в пределах точности измерений.

Введение. Модели кинематики

Введение. Система отсчета Поступательное движение – это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Введение. Система отсчета Движение тела происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась, и в какие моменты времени она проходила то или иное положение. Движение тела всегда относительно. Его можно обнаружить только в том случае, если вы будете сравнивать положение движущейся материальной точки с положением другого тела, которое считают неподвижным.

Тело отсчета. Система отсчета Тело, относительно которого рассматривается движение, называют телом отсчета. Система отсчета – совокупность системы координат и часов, связанных с телом отсчета.

Тело отсчета. Система отсчета В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами x, y, z или радиус–вектором , проведенным из начала системы координат в данную точку

Тело отсчета. Система отсчета При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями x = x(t), y = y(t), z = z(t), (1. 1) эквивалентными векторному уравнению , (1. 2) где – x, y, z – проекции радиуса – вектора на оси координат, а i, j, k - единичные векторы, направленные по соответствующим осям. Уравнения (1. 1) и соответственно (1. 2) называются кинематическими уравнениями движения материальной точки.

Тело отсчета. Система отсчета Содержание

Кинематика поступательного движения Исключая время t в уравнениях (1. 1) и (1. 2) получим уравнение траектории движения материальной точки. Траектория движения материальной точки – линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным (поступательным), криволинейным и вращательным.

Кинематика раздел механики, в котором изучаются движения тел без учета их массы и действующих на них сил. Исходными понятиями в кинематике являются такие фундаментальные физические понятия, как пространство и время. Пространство выражает порядок сосуществования отдельных физических объектов. Время порядок смены явлений.

Свойства пространства и времени задаются не философскими теориями, а являются предметом естественно-научного познания. При движении тела со скоростями много меньшими скорости света (с = 299792458 м с 1) пространство является евклидовым и время течет одинаково во всех системах отсчета. Пространство однородно и изотропно в пространстве нет выделенных направлений. Все точки пространства равноправны и все направления эквивалентны.

Однородность времени означает, что все моменты времени эквивалентны и нет какоголибо выделенного начала отсчета для протекания любого физического явления. Время однонаправлено прошлого в будущее. и протекает из При скоростях близких к скорости света, размеры предметов и временной интервал между событиями не являются инвариантами и зависят от выбора системы отсчета.

1. 2 Векторные величины Вектор представляет собой математическую величину, характеризуемую длиной и направлением. В учебниках векторы обозначаться жирными буквами, например s, а длины векторов – светлыми курсивными буквами, например s, либо в виде s. В конспектах вектора удобнее обозначать стрелкой над буквой s. Длина вектора всегда положительна.

Пусть Вектор s 1 представляет собой перемещение из точки А в точку В, а s 2 – перемещение из точки В в точку С. Результирующее перемещение s из А в С представляет собой векторную сумму s 1 + s 2. sx = s 1 x + s 2 x, sy = s 1 y + s 2 y.

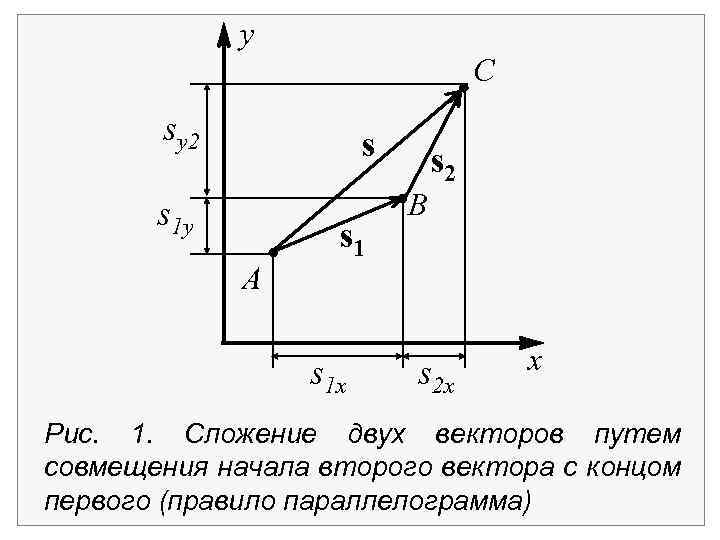
y С sy 2 s s 1 y A s 1 x s 2 B s 2 x x Рис. 1. Сложение двух векторов путем совмещения начала второго вектора с концом первого (правило параллелограмма)

Произвольный вектор r можно задать тремя его составляющими x, y, z. Общепринята следующая запись: r = ix + jy + kz, где i, j, k – единичные векторы, направленные вдоль осей x, y, z соответственно. Например, как показано на рис. 2, вектор i имеет единичную длину и направлен вдоль оси х. Рис. 2. Три единичных вектора i, j и k

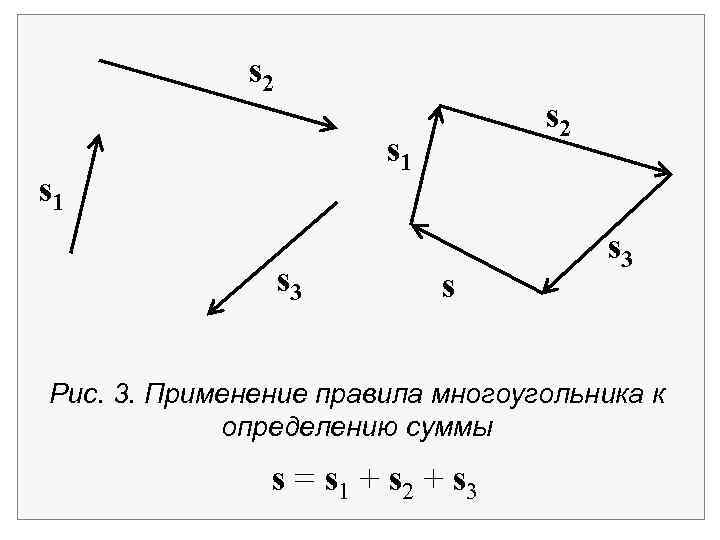
s 2 s 1 s 3 s s 3 Рис. 3. Применение правила многоугольника к определению суммы s = s 1 + s 2 + s 3

1. 3. Кинематика поступательного движения материальной точки Материальная точка физический объект, размерами которого можно пренебречь по сравнению с пройденным расстоянием. Например, радиус Земли R = 6, 4 106 м, радиус орбиты Земли r = 1, 5 1011 м. То есть Землю можно рассматривать в качестве точки на околосолнечной орбите.

Положение точки относительно прямоугольной системы координат задается радиус-вектором r = r(t), т. е. набором трех проекций координат точки на оси x, y, z, как функций времени: r = ix(t) + jy(t) + kz(t), В международной системе СИ, метрах (м). r измеряется в Линия, описывающая изменение положения конца радиус-вектора r со временем, называется траекторией движения (рис. 2. 3).

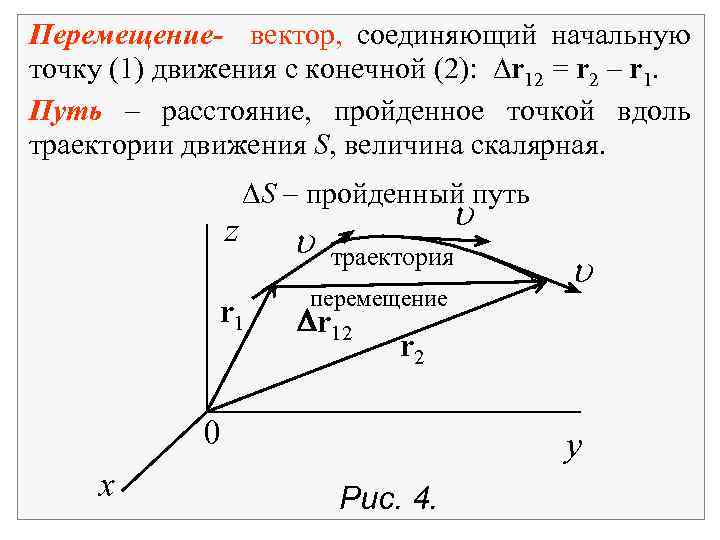
Перемещение- вектор, соединяющий начальную точку (1) движения с конечной (2): r 12 = r 2 – r 1. Путь – расстояние, пройденное точкой вдоль траектории движения S, величина скалярная. z S – пройденный путь r 1 u u траектория перемещение Dr 12 r 2 0 x u y Рис. 4.

1. 4. Мгновенная скорость Скорость – это быстрота изменения положения тела в пространстве. Мгновенная скорость равна производной от радиус-вектора тела по времени v= vx, vy, vz - проекции вектора скорости на оси x, y, z

Вектор скорости v направлен по касательной к траектории движения. Величина скорости равна: Время в СИ измеряется в секундах, длина в метрах, скорость в [метрах за секунду] = [м/с]. Средняя величина скорости точки равна отношению пути S ко времени t, за который этот путь пройден: vср = .

Векторное сложение скоростей можно продемонстрировать на примере лодки, перемещающейся в движущейся воде. Пусть r перемещение лодки относительно воды, rw перемещение воды относительно берега за время t. Тогда для перемещения r лодки относительно берега имеем r = rw + r. Разделив обе части этого выражения на t, получим v = vw + v.

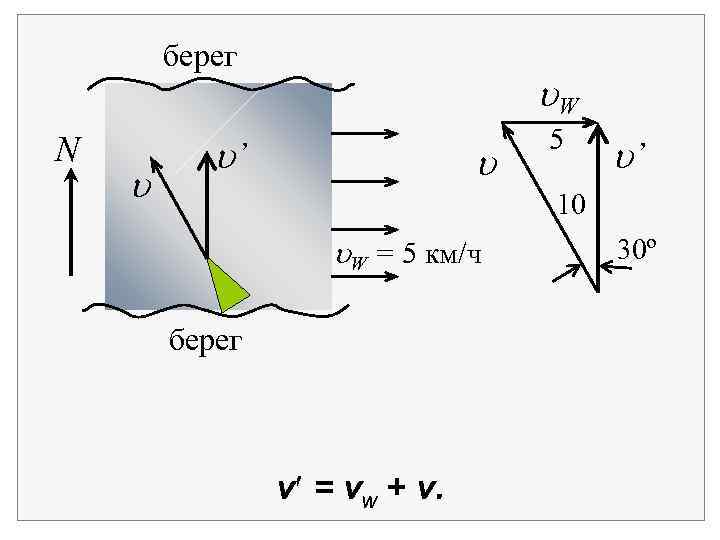
берег N u u. W u’ u 5 u’ 10 u. W = 5 км/ч берег v = vw + v. 30º

1. 5. Ускорением называется физическая величина, равная скорости изменения скорости первая производная от v по t или вторая производная от r по t: Вектор v при произвольном движении не остается постоянной со временем и может изменяться по величине и по направлению.

Введем единичный вектор (рис. ), связанный с точкой 1 и направленный по касательной к траектории движения точки 1 (векторы и в точке 1 совпадают). Тогда можно записать: Где скорости. – модуль вектора Рис. 32

Найдем общее ускорение (как производную): Получили два слагаемых ускорения: – тангенциальное ускорение, совпадающее с направлением в данной точке. – нормальное ускорение или центростремительное. 33

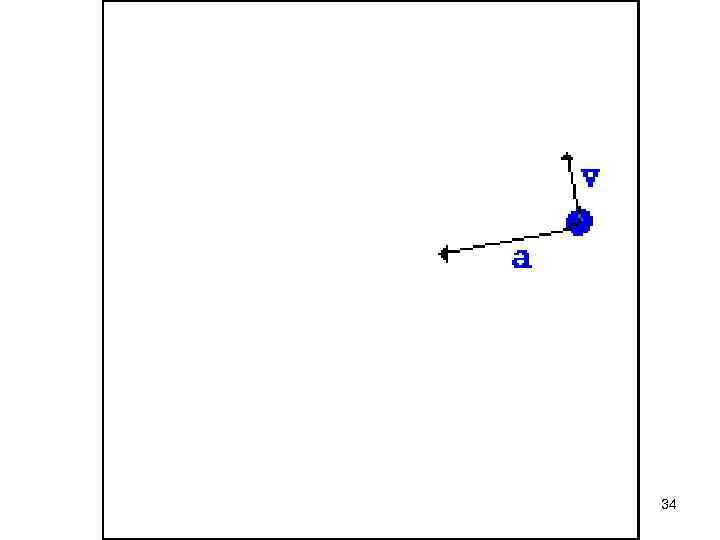
34

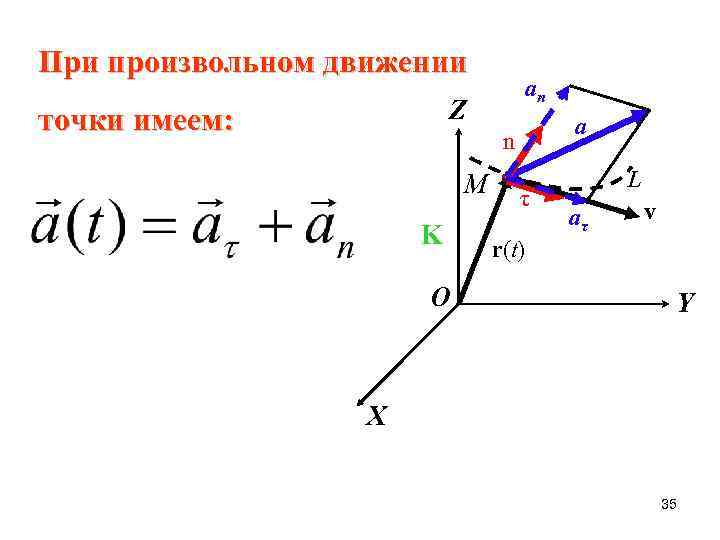
При произвольном движении an Z точки имеем: a n М K O τ L aτ v r(t) Y X 35

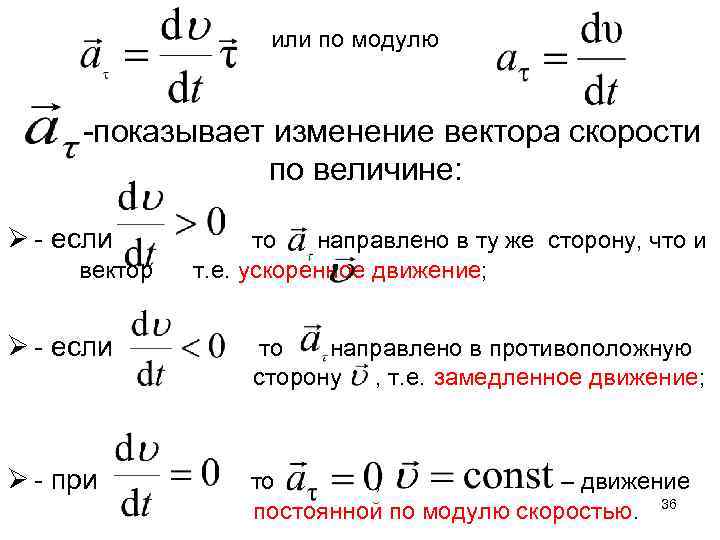
или по модулю -показывает изменение вектора скорости по величине: Ø - если вектор то направлено в ту же сторону, что и т. е. ускоренное движение; Ø - если то направлено в противоположную сторону , т. е. замедленное движение; Ø - при то , – движение постоянной по модулю скоростью. 36

Рассмотрим второе слагаемое уравнения т. е. нормальное ускорение: Нормальное ускорение определяется скоростью движения точки по окружности и степенью искривленности траекторий. 37

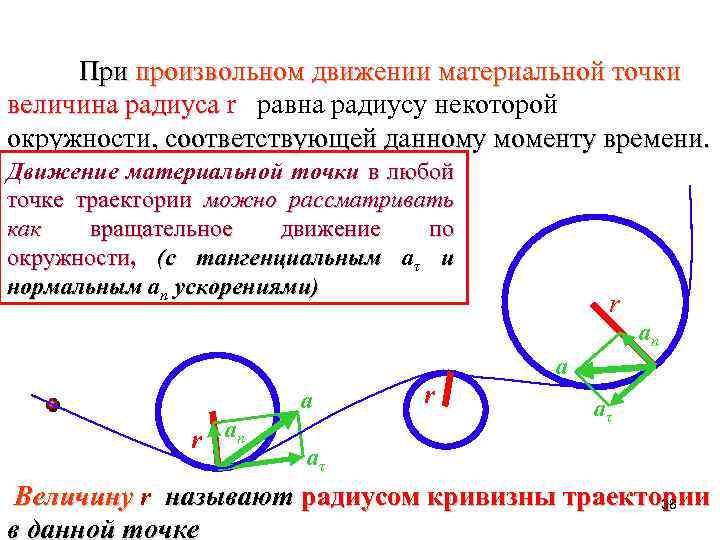
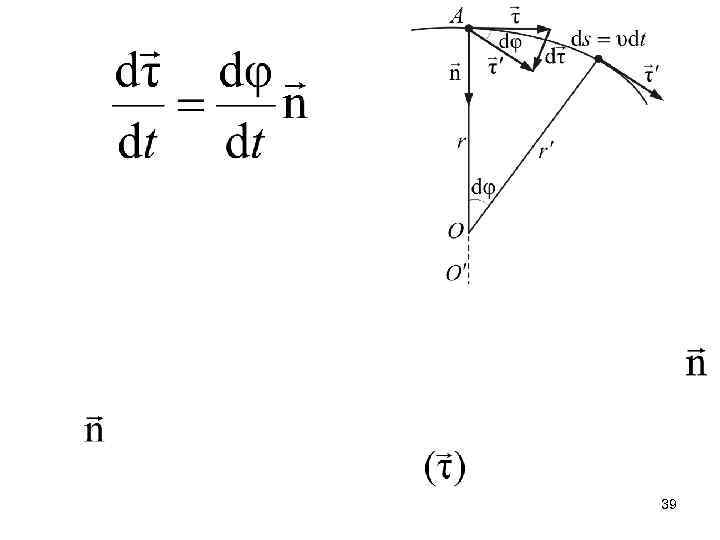
При произвольном движении материальной точки величина радиуса r равна радиусу некоторой окружности, соответствующей данному моменту времени. Движение материальной точки в любой точке траектории можно рассматривать как вращательное движение по окружности, (с тангенциальным aτ и нормальным an ускорениями) r an a r an r a aτ aτ Величину r называют радиусом кривизны траектории 38 в данной точке

39

Отсюда: Нормальное (центростремительное) ускорение показывает быстроту изменения направления вектора скорости 40

Модуль нормального ускорения: Центростремительное ускорение – движение происходит по окружности. Нормальное ускорение - движение происходит по произвольной кривой, оно перпендикулярно к касательной в любой точке 41 траектории.

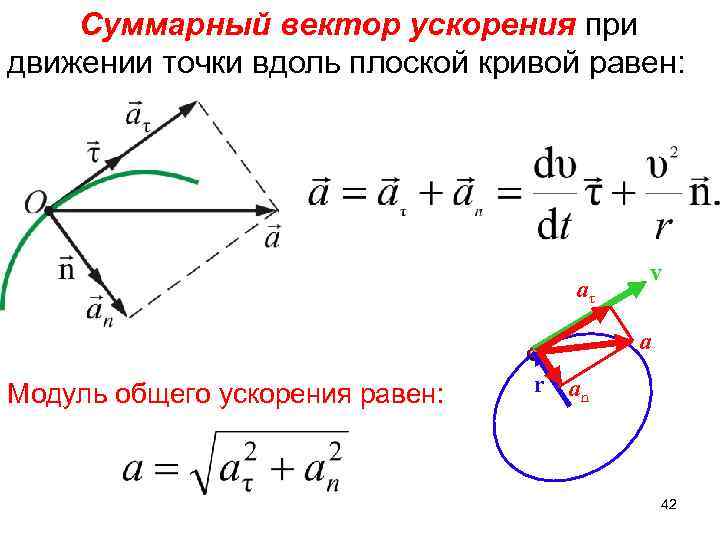
Суммарный вектор ускорения при движении точки вдоль плоской кривой равен: aτ v a Модуль общего ускорения равен: r an 42

Рассмотрим несколько предельных (частных) случаев: – равномерное прямолинейное движение; – равноускоренное прямолинейное движение; – равномерное движение по окружности. 43

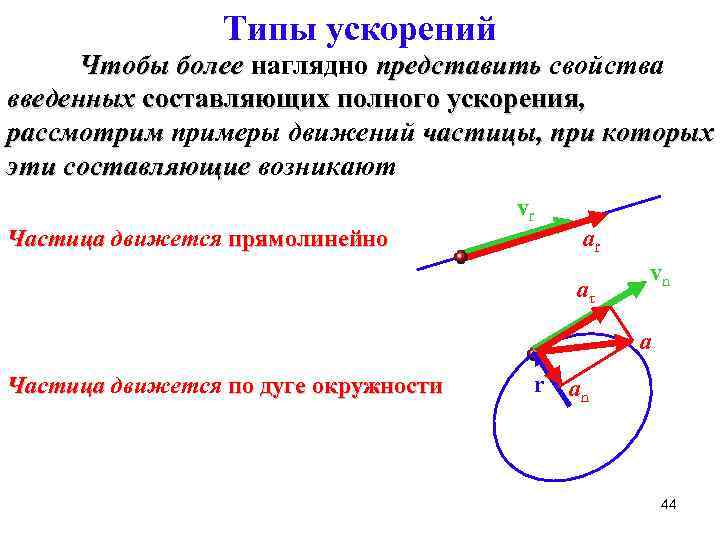
Типы ускорений Чтобы более наглядно представить свойства введенных составляющих полного ускорения, рассмотрим примеры движений частицы, при которых эти составляющие возникают Частица движется прямолинейно vr ar aτ vn a Частица движется по дуге окружности r an 44

1. 6. Кинематика вращательного движения Движение материальной точки по окружности описывается угловой скоростью и угловым ускорением . Положение точки А на окружности задаётся углом , который образует радиус-вектор r с неизменным направлением оси х (рис. 7).

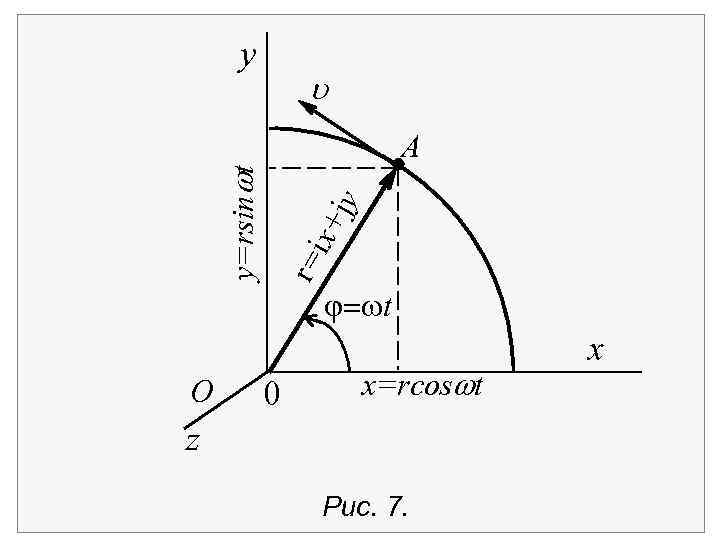
y u O jy ix+ r= y=rsinwt A 0 = t x=rcoswt z Рис. 7. x

Величина угловой скорости равна углу поворота радиус-вектора точки в единицу времени Вращение называется равномерным, если угловая скорость постоянна, в этом случае угол поворота линейно растет со временем: = 0 + t.

При равномерном вращении называют циклической частотой вращения. Число оборотов в единицу времени: Пусть точка А движется по окружности постоянного радиуса r с постоянной угловой скоростью , найдем связь между линейной и угловой скоростью.

Движение точки по круговой траектории описывается уравнением r(t) = ix(t) + jy(t) = r(i cos t + j sin t), где i, j единичные векторы, направленные вдоль осей x и y соответственно. Вектор скорости материальной точки, движущейся по окружности неизменного радиуса с постоянной скоростью, равен v

Вектор v направлен по касательной к окружности, т. е. перпендикулярно r, поскольку их скалярное произведение равно нулю (v, r) = 0. Величина вектора скорости равна

Найдем ускорение точки, равномерно вращающейся по окружности, и связанное только с изменением направления вектора скорости, т. е. нормальное ускорение an = 2 r(t). = 2 r[(i cos t + j sin t] =

Нормальное ускорение направлено к центру окружности, о чем говорит знак «минус» ( r). Величина нормального ускорения равна an = 2 r = Это ускорение также называют центростремительным ускорением. Угловое ускорение = /dt, производная по времени от угловой скорости

Угловая скорость и угловое ускорение являются в общем случае векторами. Связь между вектором угловой и линейной скорости v задается с помощью векторного произведения v = [ , r]. Вектор угловой скорости направлен перпендикулярно плоскости вращения, в сторону, определяемую правилом буравчика: если вращать буравчик по направлению движения точки, то его поступательное движение укажет направление вектора .

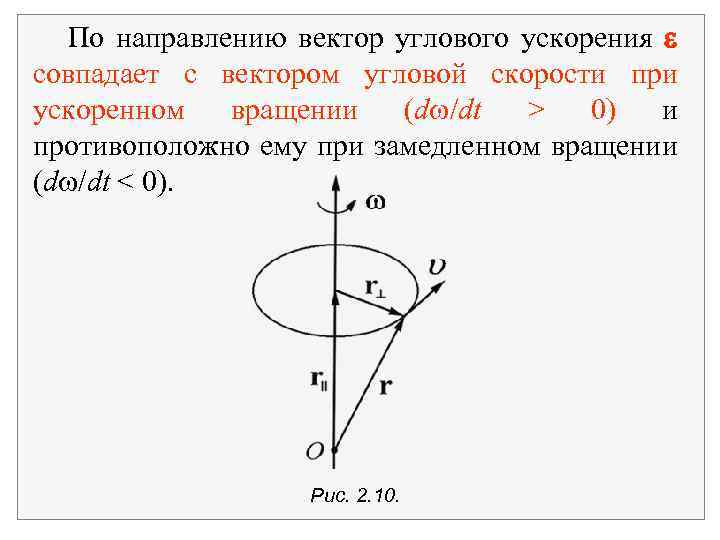
По направлению вектор углового ускорения совпадает с вектором угловой скорости при ускоренном вращении (d /dt > 0) и противоположно ему при замедленном вращении (d /dt < 0). Рис. 2. 10.

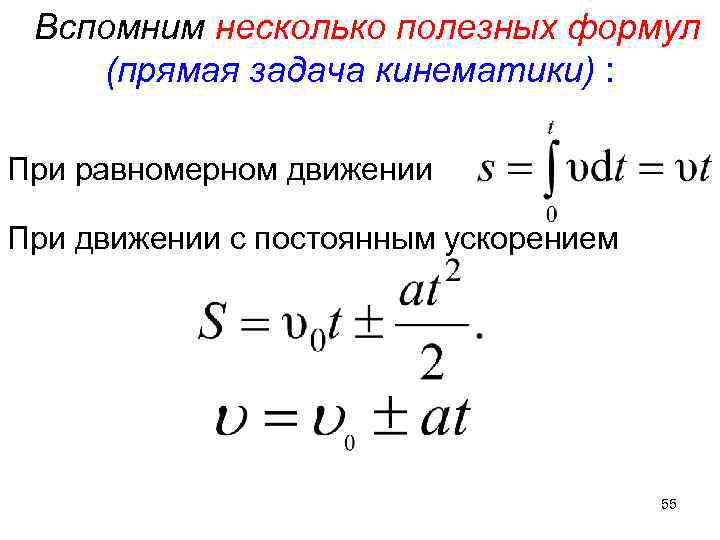
Вспомним несколько полезных формул (прямая задача кинематики) : При равномерном движении При движении с постоянным ускорением 55

Обратная задача кинематики заключается в том, что по известному значению ускорения a(t) найти скорость точки и восстановить траекторию движения r(t). По определению отсюда или, так как Следовательно

Лекция окончена Нажмите клавишу <ESC> для выхода

Кинематика твердого тела Различают пять видов движения твердого тела: - поступательное; - вращательное вокруг неподвижной оси; - плоское; - вокруг неподвижной точки; - свободное. Поступательное движение и вращательное движение вокруг оси – основные виды движения твердого тела. Остальные виды движения твердого тела можно свести к одному их этих основных видов или к 58 их совокупности.

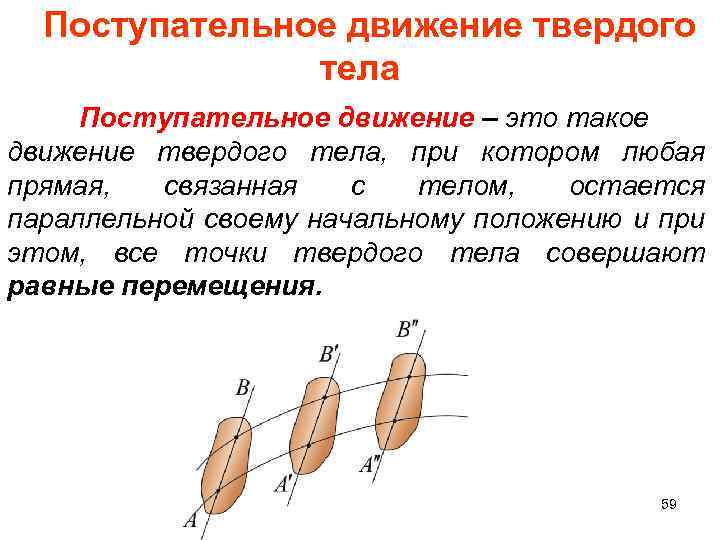
Поступательное движение твердого тела Поступательное движение – это такое движение твердого тела, при котором любая прямая, связанная с телом, остается параллельной своему начальному положению и при этом, все точки твердого тела совершают равные перемещения. 59

Скорости и ускорения всех точек твердого тела в данный момент времени t одинаковы. Это позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной точки, т. е. к задаче кинематики материальной точки, подробно рассмотренной в п. 2. 3. 60

При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой , называемой осью вращения (рисунок 2. 3). Из определения вращательного движения ясно, что понятие вращательного движения для материальной точки неприемлемо. Рисунок 2. 3 61

Вращательное движение вокруг неподвижной оси Движение твердого тела, при котором две его точки О и О' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО' называют осью вращения. Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО' Рисунок 2. 12 62

Проследим за некоторой точкой М этого твердого тела. За время точка М совершает элементарное перемещение При том же самом угле поворота другая точка, отстоящая от оси на большее или меньшее расстояния, совершает другое перемещение. Следовательно, ни само перемещение некоторой точки твердого тела, ни первая производная ни вторая производная не могут служить характеристикой движения всего твердого тела. 63

Угол поворота характеризует перемещения всего тела за время dt (угловой путь) Удобно ввести – вектор элементарного поворота тела, численно равный и направленный вдоль оси вращения ОО' так, чтобы глядя вдоль вектора мы видели вращение по часовой стрелке (направление вектора и направление вращения связаны правилом буравчика). 64

Элементарные повороты удовлетворяют обычному правилу сложения векторов: Угловой скоростью называется вектор численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении ( и всегда направлены в одну сторону). 65

Связь линейной и угловой скорости Пусть – линейная скорость точки М. За промежуток времени dt точка М проходит путь В то же время (центральный угол). Тогда, (2. 4. 2) 66

- Связь линейной и угловой скорости В векторной форме Вектор ортогонален к векторам и и направлен в ту же сторону, что и векторное произведение 67

Период Т – промежуток времени, в течение которого тело совершает полный оборот (т. е. поворот на угол ) Частота ν – число оборотов тела за 1 сек. Угловая скорость 68

Введем вектор углового ускорения для характеристики неравномерного вращения тела: . (2. 4. 3) Вектор направлен в ту же сторону, что и при ускоренном вращении а направлен в противоположную сторону при замедленном вращении (рисунок 2. 13). 69

Выразим нормальное и тангенциальное ускорения точки М через угловую скорость и угловое ускорение: 70

В кинематике решаются две задачи: • Прямая задача, когда по известной функции r(t) находится v(t) и a(t). • Обратная задача, когда по известной функции a(t) находится v(t) и r(t).