6-1-1Kolebania_i_volny.ppt
- Количество слайдов: 112

Сегодня: Sunday, February 18, 2018 Лекция Тема: КОЛЕБАНИЯ И ВОЛНЫ Содержание лекции: 1. Введение 2. Электрический колебательный контур 3. Незатухающие свободные колебания 4. Затухающие колебания 5. Вынужденные колебания. Резонанс 6. Волны 7. Волновые уравнения

1. Введение Под колебаниями в физике понимают движения или состояния, обладающие той или иной степенью повторяемости во времени. Колебания свойственны всем явлениям природы. Пульсирует излучение звезд, внутри которых идут циклические ядерные реакции. С высокой степенью периодичности вращаются планеты Солнечной системы. При этом всякое вращение (рис. 1) можно представить как два одновременных колебания во взаимно перпендикулярных направлениях x(t) = r cos t, y(t) = r sin t откуда следует x 2(t) + y 2(t) = r 2

x 2(t) + y 2(t) = r 2 уравнение окружности, по которой с угловой скоростью вращается точка М. К колебательным явлениям можно отнести приливы и отливы на Земле, вызванные периодическим вращением Луны.

Ветры возбуждают колебания на поверхности водоемов. Внутри любого живого организма от клетки до высокоразвитых популяций непрерывно идут ритмично повторяющиеся процессы – биение сердца, колебания психических состояний и т. д.

В технике колебания либо выполняют определенные функциональные обязанности – колесо, маятник, генератор и т. д. , либо возникают какнеизбежное проявлениефизических свойств– вибрации машин и сооружений, неустойчивости и т. д. В физике особенно выделяют колебания двух видов – механические и электромагнитные и их электромеханические комбинации, поскольку они чрезвычайно актуальны для жизнедеятельности человека.

Механические колебания плотности воздуха воспринимаются нами как звук, а быстрые электромагнитные колебания – как свет. С помощью звука и света мы получаем основную часть информации об окружающем нас мире. Для колебаний характерно превращение одного вида энергии в другую – кинетической в потенциальную, магнитной в электрическую и т. д. Колебания распространяются и в пространстве, в этом случае мы имеем дело с волнами. Волны – это изменение состояния среды или возмущения, распространяющиеся в этой среде и несущие с собой энергию.

Наиболее часто встречающиеся виды волн – упругие, поверхностные, электромагнитные. Частным случаем упругих волн является звук и сейсмические волны, разновидностью электромагнитных волн служат радиоволны, свет, рентгеновские лучи. Основным свойством всех волновых процессов является перенос в этих процессах энергии без переноса вещества.

Изучение колебаний и волновых процессов активно стимулировало развитие науки. Так, исследование колебаний маятника (1636 г. ) позволило Галилею более точно измерить промежутки времени. Изучение Ньютоном законов периодического обращения планет вокруг Солнца привело к созданию начал классической механики (1686 г. ).

Максвелл связал свойства электромагнитных процессов с характеристиками света и создал электромагнитную теорию света. Благодаря общности закономерностей колебательных и волновых процессов различной природы оказывается возможным вести их описание на основе единых математических моделей, не интересуясь деталями их поведения. Поскольку одинаковые уравнения имеют одинаковые решения, то результаты, полученные, например, при исследовании механических колебаний, можно перенести в оптику и радиотехнику.

Колебания могут осуществляться в широком диапазона частот и периодов Т. Так, период обращения Солнца вокруг центра Галактики Т 1011 1012 с, обращение Земли вокруг Солнца Т 3, 6 107 с, обращение Луны вокруг Земли – лунный месяц Т 2, 4 106 с, вращение Земли вокруг своей оси – сутки Т 9 104 с, опасные для человека инфразвуки 0, 2 0, 1 с, звуковые колебания, воспринимаемые человеком, 5 10 5 5 10 2 с, видимый свет Т 2, 5 10 14 1, 33 10 14 с, короткоживущие частицы резонансы Т 10 22 10 24 с.

2. Электрический колебательный контур Изучим возникновение колебаний на примере электрических цепей и покажем, что аналогичные явления могут наблюдаться в механических и других системах. Рассмотрим электрический контур (рис. 2), состоящий из сопротивления R, катушки индуктивности L, конденсатора С и генератора . Такая схема называется колебательным контуром.
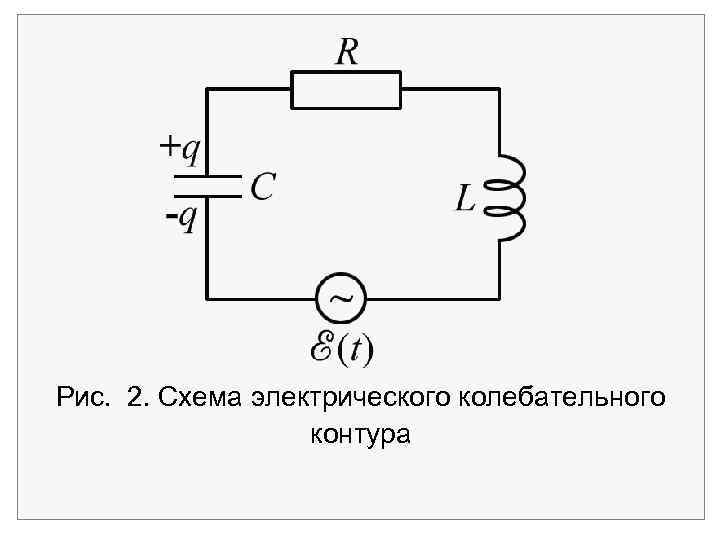
Рис. 2. Схема электрического колебательного контура

Закон Ома для данной цепи IR = 1 2 + L + (t). Цепь включает ЭДС генератора (t), ЭДС самоиндукции L. Разность потенциалов на обкладках конденсатора равна 2 1 = где q – заряд; С – емкость конденсатора.

ЭДС самоиндукции определяется индуктивностью катушки L и скоростью изменения тока в цепи Ток в цепи Подставляя в уравнение закона Ома эти величины,

получим уравнение, описывающее процессы в электрическом колебательном контуре называемым уравнением колебательного контура. Подобное уравнение получается при рассмотрении движения тела, подвешенного на пружине, под действием вынуждающей силы F(t) (рис. 3).
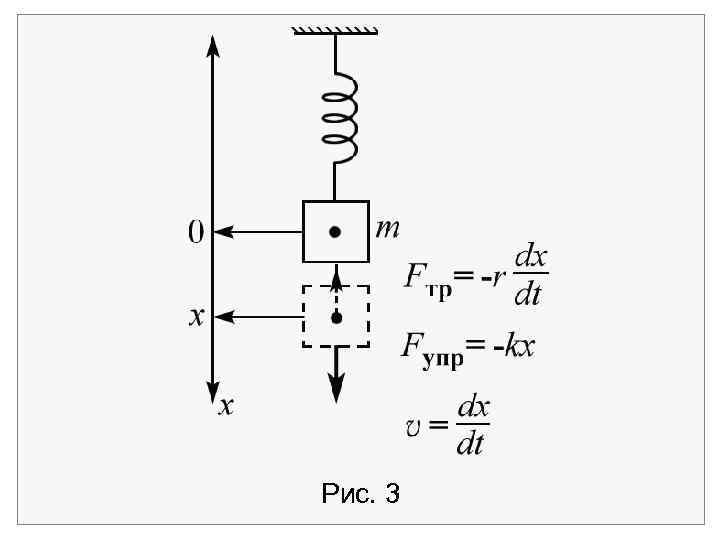
Рис. 3

В этом случае на тело действует сила упругости Fупр= kx, направленная всегда против x(t) – смещения тела из положения равновесия, и сила трения, пропорциональная скорости движения груза Fтр направленная против скорости движения.

Подставляя все эти величины во второй закон Ньютона найдем уравнение вынужденных механических колебаний

Математически полученные уравнения эквивалентны и имеют одинаковые решения. Отклонение груза от состояния равновесия в отсутствие вынуждающей силы F(t) = 0 и при r = 0 (в отсутствие силы трения) – приведет к незатухающим колебаниям груза, подвешенного на пружине. В этом случае уравнение для механических колебаний упростится

3. Незатухающие свободные колебания При отсутствии в цепи омического сопротивления (R = 0) и генератора . процесс изменения заряда со временем в колебательном контуре (рис. 4) описывается уравнением Домножив это на и введя обозначение , ( 0 -циклическая частота) можно привести его к виду:
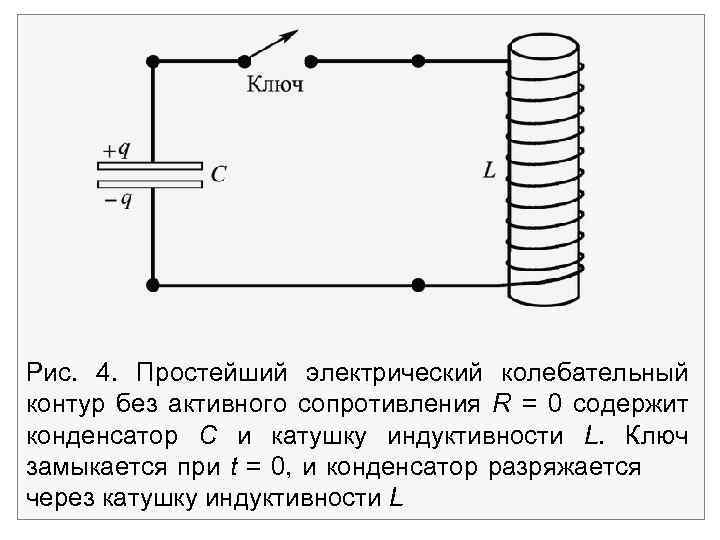
Рис. 4. Простейший электрический колебательный контур без активного сопротивления R = 0 содержит конденсатор С и катушку индуктивности L. Ключ замыкается при t = 0, и конденсатор разряжается через катушку индуктивности L

Решение этого уравнения, описывающего колебания заряда в LC-контуре, имеет вид q = q 0 cos( 0 t + ). Постоянные q 0 и определяются начальными условиями, например значениями тока и заряда при t = 0. Полученное соотношение описывает и движение груза на пружине ( r и F(t) равны нулю) если сопоставить q x, L m, 1/C k, x = x 0 cos( 0 t + ). ,

Возникновение колебаний в контуре, состоящем из емкости С и индуктивности L, связано с периодическим превращением энергии электрического поля, сосредоточенного между обкладками конденсатора , в энергию магнитного поля и обратно благодаря наличию инерционного элемента – индуктивности.

Первоначально локализованный на обкладках конденсатора заряд начинает разряжаться через катушку индуктивности. Благодаря явлению самоиндукции ток в цепи нарастает постепенно до тех пор, пока вся энергия конденсатора не превратится в энергию магнитного поля. В этот момент заряд на обкладках конденсатора станет равным нулю, а ток в катушке индуктивности достигнет максимума.

Далее ток, не изменяя направления, начнет убывать, но в силу явления электромагнитной индукции ток не сразу упадет до нуля, а будет спадать постепенно. При этом нижняя пластина конденсатора будет постепенно заряжаться положительно, а верхняя отрицательно.

Возникающее электрическое поле будет тормозить движение зарядов, и постепенно ток в цепи упадет до нуля. В этот момент заряд на обкладках конденсатора и энергия электрического поля достигнут максимума, а энергия магнитного поля вновь станет равной нулю. Но заряд на обкладках конденсатора уже сменил знак. К этому времени завершится первый полупериод в колебательном контуре (рис. 5).
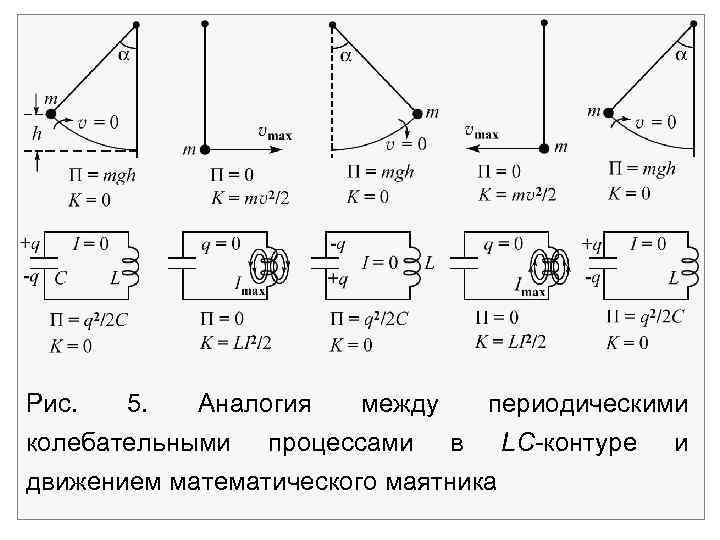
Рис. 5. Аналогия между периодическими колебательными процессами в LC контуре и движением математического маятника

Во время второго полупериода ток течет в обратном направлении, увеличивая энергию магнитного поля, как только ток достигнет максимума, начнется новая перезарядка конденсатора. Эти процессы перезарядки можно сопоставить с колебаниями маятника, где максимальное отклонение тела от положения равновесия соответствует максимальному заряду конденсатора, а максимальная кинетическая энергия маятника в нижней точке траектории аналогична полному переходу энергии конденсатора в энергию магнитного поля максимальному току в цепи.

В колебательном контуре без активного сопротивления сумма энергий электрического и магнитного полей, запасенных в конденсаторе и катушке индуктивности, остается постоянной.

Свободные незатухающие колебания совершаются системой по закону синуса или косинуса называются гармоническими колебаними. Система возвращается в исходное состояние через минимальное время Т 0 период колебаний q(t + T 0) = q(t). Для гармонических колебаний

Число колебаний в единицу времени называется частотой колебаний собственная или резонансная частота колебательного контура. Единицей измерения частоты колебаний служит Герц [Гц]=1/[с]. Частоте в один герц соответствует частота, при которой за секунду происходит одно полное колебание. Величина q 0 называется амплитудой, а 0 t + фазой колебаний. Постоянная начальная фаза колебаний.
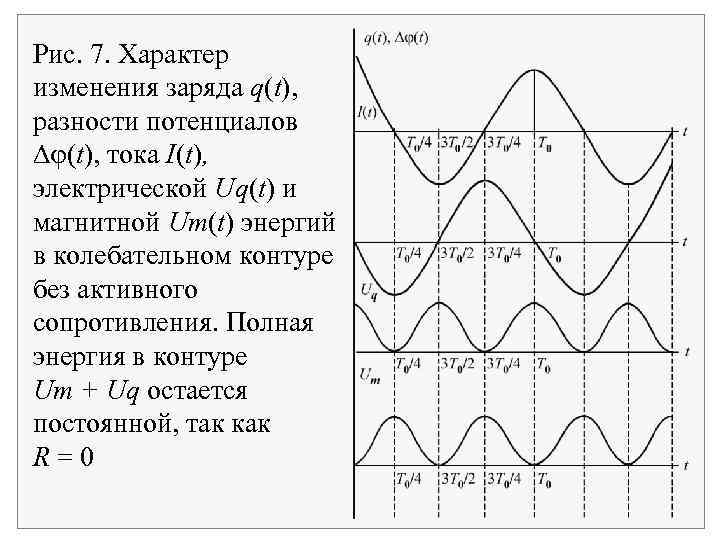
Рис. 7. Характер изменения заряда q(t), разности потенциалов (t), тока I(t), электрической Uq(t) и магнитной Um(t) энергий в колебательном контуре без активного сопротивления. Полная энергия в контуре Um + Uq остается постоянной, так как R=0

4. Затухающие колебания Колебательный контур всегда обладает сопротивлением R (рис. 8), если подводящие провода и катушка индуктивности собраны не из сверхпроводящих материалов. Проходя по такой цепи, ток выделяет джоулево тепло и расходует энергию, первоначально запасенную в колебательной системе. Колебания в такой системе описываются уравнением, аналогичным незатухающим, но с добавлением слагаемого, описывающего потери энергии на сопротивлении RI:
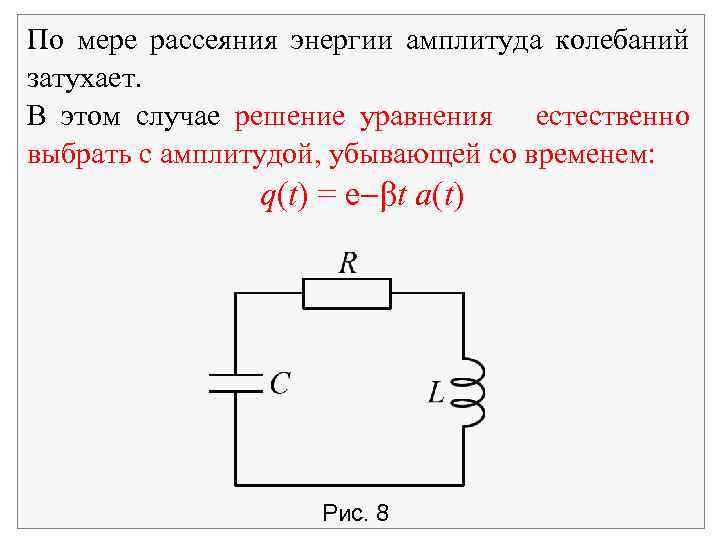
По мере рассеяния энергии амплитуда колебаний затухает. В этом случае решение уравнения естественно выбрать с амплитудой, убывающей со временем: q(t) = e t a(t) Рис. 8

Разделим уравнение на L и введем обозначения: 2 R/L, 02 1/СL, - коэффициент затухания. Уравнение преобразуется к виду Подставив в него q(t) = e ta(t), придем к уравнению для переменной a(t):

Если величина 2 = 02 2 > 0, то решение уравнения совпадает с ранее найденным для незатухающих колебаний: a(t) = q 0 cos( t + ). Величина заряда на обкладках конденсатора описывается зависимостью q(t) = q 0 e t cos( t + ). Функция q(t) не периодична в смысле q(t) = q(t + T), но она периодически обращается в нуль через равные промежутки времени Т/2 = /.

Величину Т = 2 / называют периодом затухающих колебаний в смысле периодического обращения заряда в нуль Сопротивление цепи понижает частоту колебаний в контуре и увеличивает период колебаний тем сильнее, чем больше отношение

Множитель q 0 e t называется амплитудой затухающих колебаний. Амплитуда колебаний при наличии сопротивления экспоненциально убывает со временем(рис. 9). Если сопротивление цепи так велико, что , то процесс изменения заряда в цепи не будет колебательным, а станет апериодическим.
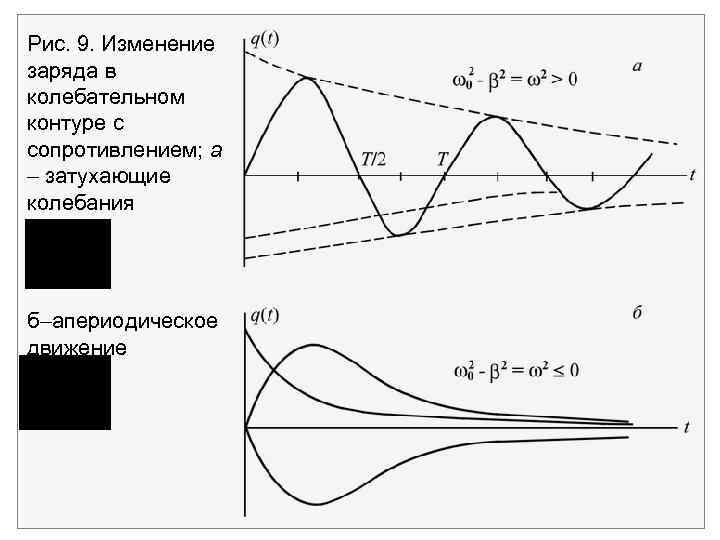
Рис. 9. Изменение заряда в колебательном контуре с сопротивлением; а затухающие колебания б апериодическое движение

Затухание колебаний характеризуется логарифмическим декрементом затухания . Он равен натуральному логарифму отношения амплитуд колебаний, отличающихся по времени измерения на период Здесь a(t) амплитуда колебаний изучаемой величины, например q, I, U и пр.

Время , по истечении которого амплитуда колебаний убывает в е раз, называется временем затухания: За время система совершит N полных колебаний, где Таким образом, логарифмический декремент затухания связан с числом колебаний N, приводящим к уменьшению амплитуды в е раз соотношением

Подставляя в выражение для значения и , получаем Если затухание в системе невелико , то

Важнейшей характеристикой колебательного контура является добротность Q, величина, обратно пропорциональная логарифмическому декременту: Чем выше добротность, тем большее число колебаний успеет совершить система, прежде чем амплитуда колебаний уменьшится в е (2, 71826) раз. При слабом затухании Добротность тем выше, чем меньше относительные потери энергии в контуре за период.

Все математические результаты, полученные для электрических затухающих колебаний, полностью применимы и к механическим затухающим колебаниям, описываемым уравнением и имеющим решение x(t) = x 0 e t cos( t + ), где 2 = 02 2, = r/2 m, Потери энергии колебаний в механических системах также вызваны ее превращением в теплоту вследствие трения.

5. Вынужденные колебания. Резонанс. Вынужденные колебания в контуре, состоящем из сопротивления R, емкости С, индуктивности L возникают, если эта цепочка подключена к источнику электродвижущей силы (t), величина которой меняется со временем t. В этом случае уравнение колебаний становится неоднородным, поскольку содержит ненулевую правую часть

Разделив уравнение на L и вводя прежние обозначения , к виду , приведем его Решим это уравнение для зависимости (t) в виде (t) = 0 cos t, где 0, постоянные величины, а величина называется частотой внешней вынуждающей силы.

Решением этого уравнения: где амплитуда вынужденных колебаний;

Сдвиг фаз вынужденного колебания Необычным и новым в полученных решениях является немонотонная зависимость амплитуды колебаний в системе от частоты вынуждающей силы .

Особенно ярко это проявляется при отсутствии потерь энергии в системе В этом случае приближении частоты вынуждающей силы к частоте соответственных колебаний 0 амплитуда колебаний начинает очень сильно возрастать – наступает резонанс (франц. resonance, от лат. resonо откликаюсь)

Резонанс в акустических и механических явлениях впервые был описан итальянским ученым Г. Галилеем, а в электромагнитных системах – на примере колебательного контура в 1868 г. английским ученым Дж. Максвеллом. Резонанс наступает тогда, когда внешняя периодическая сила (ЭДС) изменяется с частотой , близкой к частоте собственных колебаний 0 системы.

Реально всегда существуют причины, ограничивающие амплитуду колебаний в условиях резонанса. Это связано с диссипацией энергии (R 0) из-за наличия сопротивления и сил трения. Резонансная частота для заряда и напряжения на конденсаторе при наличии сопротивления определяется из условия dq 0/d = 0 и равна

Амплитуда колебаний при резонансе тем больше, чем меньше сопротивление цепи и выше амплитуда переменной ЭДС: здесь статическое значение заряда при постоянной ЭДС ( = 0).

Зависимость амплитуды колебания q(t) от частоты внешней вынуждающей силы называется резонансной кривой. Важной характеристикой резонансной кривой является ширина резонансной кривой = 2 1, где 1, 2 частоты, при которых энергия колебаний вдвое меньше энергии в максимуме (рис. 10).
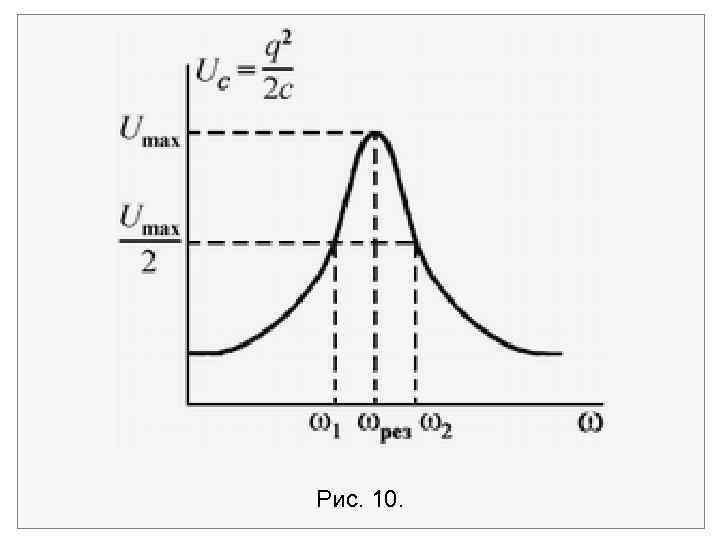
Рис. 10.

Отношение максимального значения амплитуды колебаний qрез к статистическому смещению qст равно добротности колебательного контура (при условии 2/ 02 << 1) Q= чем выше добротность колебательной системы, тем выше амплитуда колебаний при резонансе по сравнению со статистическим смещением в системе.
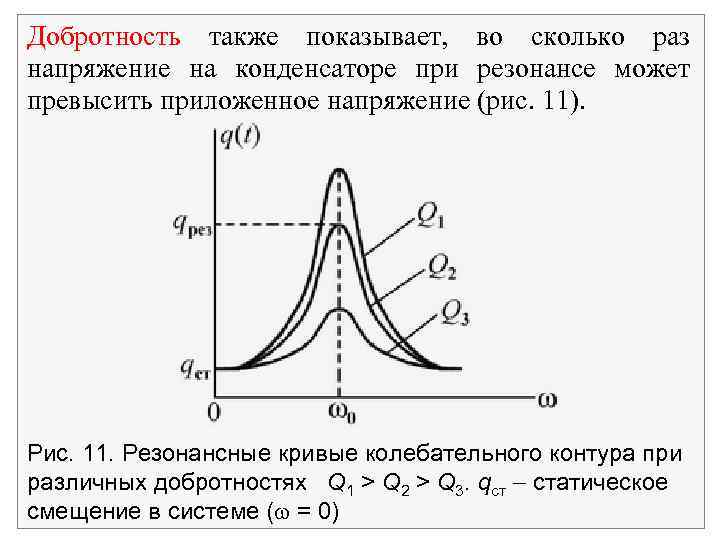
Добротность также показывает, во сколько раз напряжение на конденсаторе при резонансе может превысить приложенное напряжение (рис. 11). Рис. 11. Резонансные кривые колебательного контура при различных добротностях Q 1 > Q 2 > Q 3. qст статическое смещение в системе ( = 0)

Явление резонанса играет большую роль в природе, науке и технике. Резонанс сооружений и машин при периодических внешних воздействиях может стать причиной катастроф. Чтобы избежать резонансного воздействия, подбирают соответствующим образом свойства системы или используют успокоители колебаний. В случае вынужденных механических колебаний уравнение, описывающее поведение колебательной системы, имеет вид

Общее решение его имеет вид x(t) = A( )cos( t ) где амплитуда установившихся механических колебаний под действием периодической силы, воздействующей с циклической частотой и амплитудой Fа.

Если частоты и 0 близки друг к другу и их полуразность равна , то в этом случае система будет совершать под действием вынужденной силы колебания с частотой, близкой к собственной частоте колебаний в системе. Амплитуда колебаний будет медленно и периодически изменяться со временем.

Это явление называется биениями. Период повторения биений равен (рис. 12, 13). Рис. 12. Возникновение биений при сложении двух незатухающих колебаний одного направления с близкими частотами и равными амплитудами Рис. 13. Процесс установления колебаний в системе при наличии сил трения и действии вынуждающей силы

В конце концов колебания перейдут в колебания постоянной амплитуды.

6. Волны- это изменения некоторой совокупности физических величин, способных распространяться от места их возникновения или колебаться в ограниченной области пространства. Как правило, при волновых движениях распространение возмущений не сопровождается переносом среды или вещества, в котором они возникают.

Для механических волновых движений необходима среда переноса, поскольку волна является возмущением этой среды. Но в случае электромагнитных волн в вакууме такая среда отсутствует, поскольку переменное электрическое поле порождает в свободном пространстве переменное магнитное поле, а оно, в свою очередь, вновь создает переменное электрическое поле. Гравитационные волны служат проявлением геометрических свойств пространства-времени.

Важным свойством волновых движений является наличие близкодействующей связи между возмущениями в соседних точках пространства. Так, подъем поверхности воды приводит к нарушению равновесия в соседних областях, а стремление восстановить равновесие в жидкости под действием силы тяжести приводит к возмущению новых частиц жидкости и проявляется как распространение волны. В электромагнитной волне изменение напряженности электрического поля в одной точке порождает магнитное поле в соседних точках и наоборот.

Во всем обширном семействе волновых движений можно отметить некоторые общие свойства и понятия, которые не зависят от их физической природы. Эта общность проявляется прежде всего в том, что волновые движения различных физических объектов описываются одинаковыми уравнениями.

7. Волновые уравнения Пусть в момент времени t 1 = 0 в точке с координатой х возникло некоторое возмущение всплеск на воде, удар барабана, переменное электрическое поле и т. д. , способное распространяться вдоль оси х вправо со скоростью v. Форма этого возмущения описывается в момент времени t 1 = 0 в точке с координатой х1 функцией f(x 1), где f(x 1) может быть смещением точки из положения равновесия, отклонением давления от среднего значения, напряженностью электрического или магнитного поля и т. д.

Если возмущение распространяется без искажений со скоростью v вправо, то функция f должна таким образом зависеть от х и t, чтобы выполнялись соотношения f(x 1, t 1) = f(x 2, t 2) возмущение переходит из точки x 1, t 1 в точку x 2, t 2, не меняя формы, где x 2 = x 1 + v(t 2 t 1) , откуда x 1 = x 2 v (t 2 t 1),

Оба эти уравнения эквивалентны, поскольку из первого следует второе, а из второго первое. Если возмущение распространяется вправо, то функция f зависит лишь от комбинации аргументов xиt f = f 1(x vt). Действительно, одному значению аргумента a = x vt соответствует одно значение функции f(a). Положение координаты х = а + vt этого возмущения распространяется вправо со скоростью

Если возмущение движется влево, то оно описывается уравнением f = f 2(x + vt), поскольку из условия, что одинаковому значению аргумента а соответствуют равные значения функции, следует f(x + vt) = f(a). Координата этого возмущения смещается влево x = a t со скоростью (рис. 14).
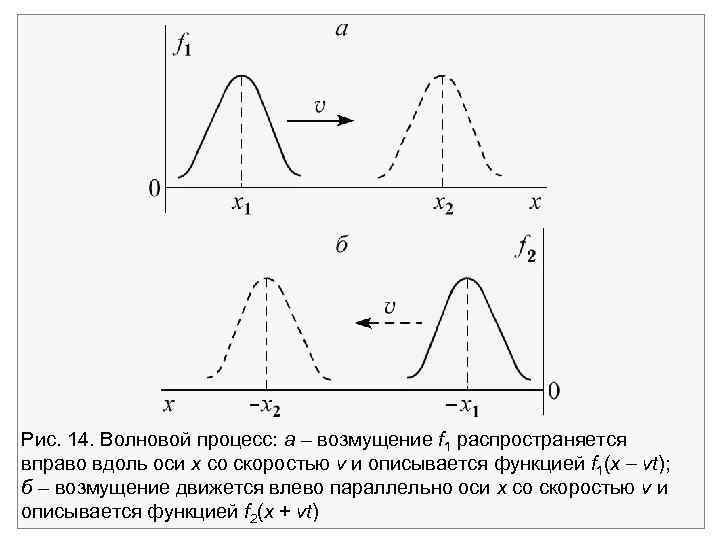
Рис. 14. Волновой процесс: а – возмущение f 1 распространяется вправо вдоль оси х со скоростью v и описывается функцией f 1(x vt); б – возмущение движется влево параллельно оси x со скоростью v и описывается функцией f 2(x + vt)
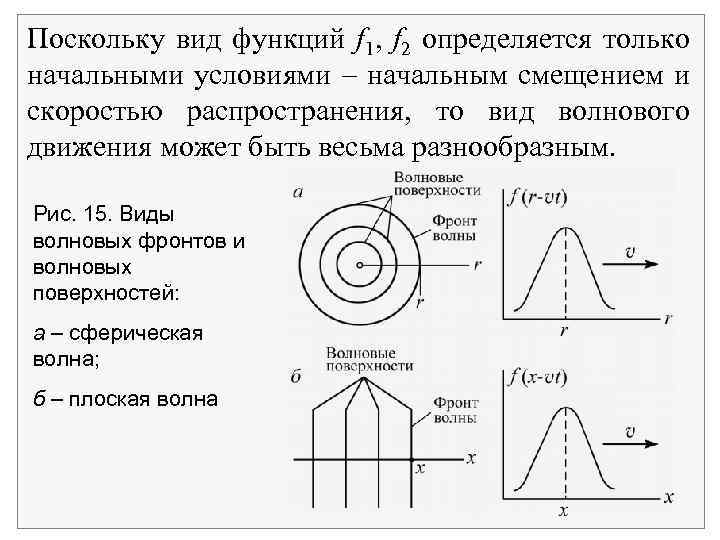
Поскольку вид функций f 1, f 2 определяется только начальными условиями начальным смещением и скоростью распространения, то вид волнового движения может быть весьма разнообразным. Рис. 15. Виды волновых фронтов и волновых поверхностей: а – сферическая волна; б – плоская волна

Геометрическое место точек, до которых доходит возмущение в момент времени t, называется фронтом волны. Фронт волны отделяет часть пространства, вовлеченного в волновой процесс, от области, куда возмущение еще не дошло. Распространение волны происходит в направлении нормали к волновому фронту и может рассматриваться как движение волнового фронта (рис. 15).

Геометрическое место точек, колеблющихся в одинаковой фазе или одинаковым образом, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченную волновым процессом. Волновых поверхностей бесконечно много, в то время как волновой фронт в каждый момент времени существует только один. Волновые поверхности и волновые фронты могут быть любой формы. В простейших случаях они имеют вид сферы или плоскости.

В этих случаях их называют соответственно сферическими или плоскими волнами (рис. 15). Распространение возмущения в пространстве можно описать при помощи дифференциального уравнения. В одномерном случае Этому уравнению удовлетворяют функции f 1(x vt), f 2(x + vt) и их суперпозиция f 1(x vt) + f 2(x + vt). Полученное уравнение называется волновым уравнением.

Плоские электромагнитные волны В свободном пространстве без токов и зарядов система уравнений Максвелла принимает вид , , div. D = 0, div. B = 0. Пусть векторы поля зависят только от координат х и t. В этом случае систему уравнений можно расписать в виде системы телеграфных уравнений , , , и уравнений

описывающих статические электрические и магнитные поля вдоль направления х распространения волны. Эти поля можно не учитывать. Полученные уравнения распадаются на две группы. В первой переменное магнитное поле с составляющей Hy порождает переменное электрическое поле с составляющей Ez, во второй переменное магнитное поле Hz порождает электрическое поле Ey. Таким образом, в плоской волне векторы E и H взаимно перпендикулярны и удовлетворяют уравнениям

Плоская электромагнитная волна. Векторы E, H, υ взаимно перпендикулярны Из общей теории волновых уравнений следует, что множитель есть величина, И обратная квадрату скорости распространения з электромагнитной волны в о б щ среде: где е й распространения света т скорость в вакууме.

Ещё раз отметим, что этот фундаментальный результат привел Максвелла к заключению, что видимый свет представляет электромагнитную волну достаточно высокой частоты = с/ = (3, 9 7, 5) 1014 Гц. Длины волн света были определены Т. Юнгом в конце XVIII в. в опытах по интерференции = 0, 4 0, 76 мкм. Векторы H, E, υ взаимно перпендикулярны и связаны соотношениями E = 0[υ, H], H = 0[υ, E].

Одним из возможных решений полученной системы уравнений является синусоидальная гармоническая электромагнитная волна, распространяющаяся от источника в положительном направлении оси х: E = E 0 cos( t – kx + 1), H = H 0 cos( t – kx + 2), где частота; k волновое число; 1, 2 начальные фазы колебаний; Е 0, Н 0 амплитуды колебаний.

Подставляя решения в исходную систему уравнений, получаем k. E 0 sin( t – kx + 1) = 0 H 0 sin( t – kx + 2), k. H 0 sin( t – kx + 2) = 0 E 0 sin( t – kx + 1). Для того чтобы эта система удовлетворялась, необходимо равенство фаз 1 = 2 и выполнение соотношений k. E 0 = 0 H 0, 0 E 0 = k. H 0. Таким образом, в электромагнитной волне колебания электрического и магнитного полей происходят с одинаковой фазой ( 1 = 2) и между амплитудами колебаний в вакууме выполняется соотношение (в СИ)

Электромагнитная волна переносит энергию, плотность потока которой определяется вектором Умова – Пойнтинга S = [E, H] [Вт/м 2]. Вектор S может быть записан через удельную плотность энергии w: S = wυ, где

Поскольку энергия и масса связаны соотношением Эйнштейна E = mс2, то электромагнитное поле обладает массой с плотностью w/с2 и импульсом с плотностью: Импульс электромагнитных волн проявляется, в частности, в световом давлении [Па].

Здесь r коэффициент отражения, который можно определить как отношение квадратов амплитуд напряженностей электрического поля в отраженной Е 0 и падающей Е 0 волнах: r = (Е 0 /Е 0)2 или как отношение потока излучения, отражённого телом, к упавшему на него потоку излучения.
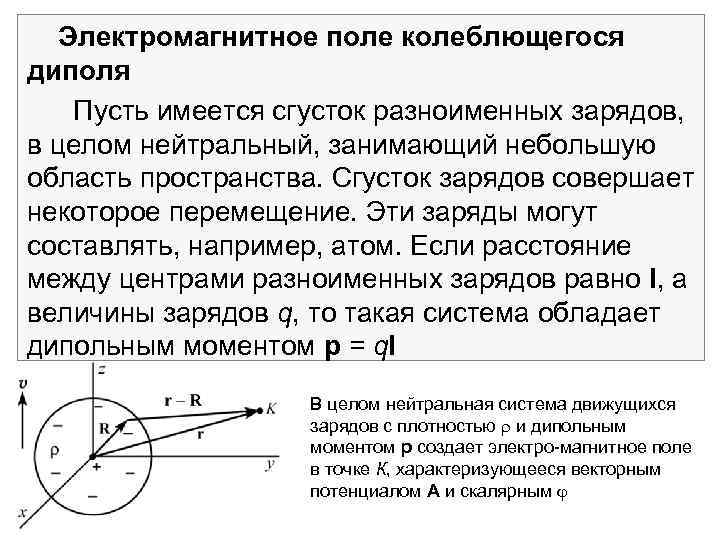
Электромагнитное поле колеблющегося диполя Пусть имеется сгусток разноименных зарядов, в целом нейтральный, занимающий небольшую область пространства. Сгусток зарядов совершает некоторое перемещение. Эти заряды могут составлять, например, атом. Если расстояние между центрами разноименных зарядов равно l, а величины зарядов q, то такая система обладает дипольным моментом р = ql В целом нейтральная система движущихся зарядов с плотностью и дипольным моментом р создает электро магнитное поле в точке К, характеризующееся векторным потенциалом A и скалярным

Здесь r коэффициент отражения, который можно определить как отношение квадратов амплитуд напряженностей электрического поля в отраженной Е 0 и падающей Е 0 волнах: r = (Е 0 /Е 0)2 или как отношение потока излучения, отражённого телом, к упавшему на него потоку излучения.

Движение такой системы зарядов может быть, например, вынужденным колебательным движением электронов атома в электрическом поле световой волны. Найдем поле, создаваемое такой системой зарядов в точке К, расположенной на расстоянии r, значительно превосходящем размеры системы R << r. Для далеких точек поправки, основной вклад в В и Е дают слагаемые, убывающие обратно пропорционально первой степени с расстоянием r. Это так называемая волновая зона излучения диполя. В волновой зоне индукция магнитного поля и напряженность электрического поля равны
![Из этих соотношений следует E = c[B, n], здесь n = r/r единичный вектор, Из этих соотношений следует E = c[B, n], здесь n = r/r единичный вектор,](https://present5.com/presentation/145977303_137157148/image-87.jpg)
Из этих соотношений следует E = c[B, n], здесь n = r/r единичный вектор, направленный вдоль радиус вектора r. Видно, что векторы B и E взаимно перпендикулярны и перпендикулярны r. Вектор E лежит в плоскости меридиана, а B направлен по параллели.

Плотность потока электро агнитной энергии, м излучаемой диполем, вектор Пойнтинга равен В сферической электромагнитной волне, излучаемой ускоренно двигающимися зарядами, векторы B направлены по параллелям, векторы E по меридианам, поток энергии S по нормали n
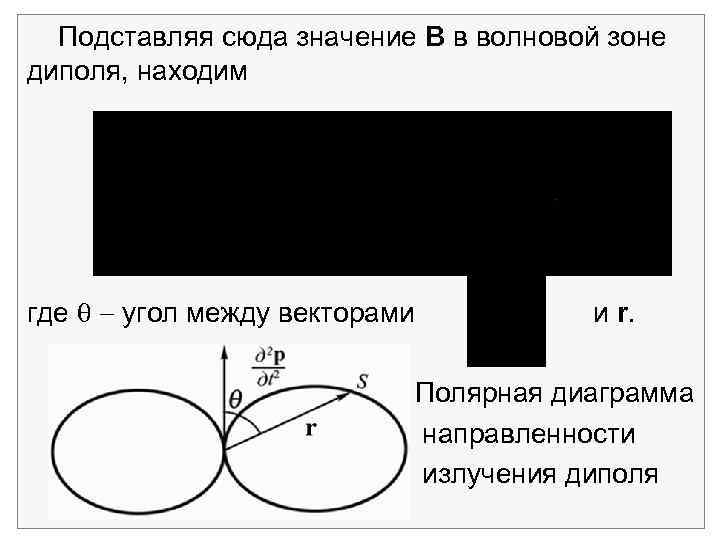
Подставляя сюда значение В в волновой зоне диполя, находим где угол между векторами и r. Полярная диаграмма направленности излучения диполя

Таким образом, ускоренно двигающиеся заряды излучают электромагнитную энергию в окружающее пространство. Вектор S направлен вдоль радиуса r и убывает обратно пропорционально r 2. Излучение максимально в направлении, перпендикулярном вектору , и отсутствует вдоль вектора. «Диаграмма направленности» для диполя имеет вид двух симметричных лепестков. Полная энергия, излучаемая ускоренно двигающимися зарядами в единицу времени, интегральная мощность излучения W, равна интегралу от модуля S, умноженному на элемент площади 2 r 2 sin d поверхности сферы:

В случае гармонических колебаний диполя (r = 0) p = p 0 cos t Имеем После усреднения по времени находим среднюю мощность излучения колеблющегося диполя

Мощность излучения растет пропорционально четвертой степени частоты = /2. Для повышения мощности излучения следует увеличивать частоту колебаний в электрическом контуре. При частоте колебаний 1 = 50 Гц испускаемая длина волна 1 = c/ 1 = 6 106 м. Такие волны практически не излучаются. Но при увеличении частоты колебаний до 2 = 3 108 Гц ( 2 = 1 м) мощность излучения увеличивается в ( 2/ 1)4 = (6 106)4 13 1026 раз.

Точечный диполь, дипольный момент которого быстро изменяется со временем, является простейшей системой излучающей электромагнитные волны. Такой диполь называется диполем Герца по имени Г. Герца, впервые рассчитавшего и изучившего электромагнитное поле. Важность этого результата, полученного Герцем, состоит в том, что любая реальная излучающая система антенна с переменным током может быть разбита на электромагнитные токи, каждый из которых излучает, как диполь Герца. Воспользовавшись принципом суперпозиции, можно найти поле всей излучающей системы.

Если диполь состоит из неподвижного точечного заряда +q, находящегося в точке r 0, и подвижного отрицательного –q, расположенного в точке r, то дипольный момент такой системы равен p = q(r – r 0). Поскольку r 0 = const, то где υ скорость; a ускорение заряда –q. В этом случае излучаемая мощность равна ускоренно двигающийся заряд излучает электромагнитную энергию пропорционально

Лекция окончена Нажмите клавишу <ESC> для выхода

Лекция окончена Нажмите клавишу <ESC> для выхода

Решением этого уравнения являются функции, будучи дважды продифференцированными, переходит вновь в себя, при этом они изменяют знак и приобретают некоторый множитель. Такими функциями являются Acos( 0 t + ), Asin( 0 t + ), и их линейные комбинации. Но фактически это все одна функция, поскольку косинус всегда можно свести к синусу , а синус может быть выражен через экспоненты с мнимым показателем:

Соответствующий электрический аналог – это колебательный контур без сопротивления R = 0 и генератора (t) = 0, описываемый уравнением (рис. 4)

Постоянные интегрирования и А определяются начальными условиями. Во многих случаях намного удобнее пользоваться решениями комплексного переменного. Умножим уравнение на виду в виде функций и преобразуем его к

Откуда следует, что стоящая в квадратных скобках величина не изменяется со временем: где q 0 – константа (максимальный заряд на обкладках конденсатора). Если переписать это уравнение в виде то оно приобретает вид закона сохранения энергии:

Преобразуем полученное уравнение к виду откуда получаем После интегрирования находим где новая постоянная.

Величины q 0, определяются начальными условиями в системе, а величины 0, Т 0 зависят от индуктивности L и емкости С колебательного контура, но не зависят от начальных условий. Период колебаний электрического контура без сопротивления равен Полученная формула для Т 0 называется формулой Томсона. Определим собственную частоту контура, составленного из катушки индуктивности и конденсатора (рис 6).
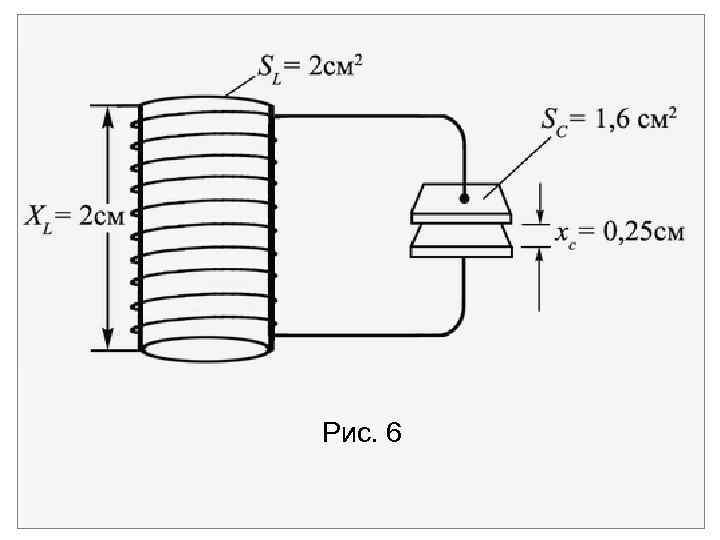
Рис. 6

Индуктивность соленоида равна = 1, 26 10 6 Гн. Емкость плоского конденсатора = 5, 67 10 13 Ф. Собственная частота колебаний с = 188 МГц.

Эта частота соответствует каналу в метровом диапазоне телевидения. Аналогичные колебательные контуры используются для настройки телевизоров на других каналах. Зная зависимость заряда на обкладках конденсатора от времени q(t), можно найти все характеристики системы ток, разность потенциалов на обкладках конденсатора, электрическую и магнитную энергии. Изменения электрической и магнитной энергий происходит с удвоенной частотой 2 0 по сравнению с частотой изменения тока, заряда, разности потенциалов 0 (рис. 7).

При достижении электрической энергией максимума магнитная энергия минимальна и наоборот. Говорят, что величины Um и Uq колеблются в противофазе. Сумма этих энергий постоянна:

Общее решение неоднородного уравнения можно представить в виде суммы общего решения однородного уравнения , , и любого частного решения неоднородного уравнения. q(t) исходного

Будем искать частное решение этого уравнения в виде q(t) = q 0 ei t. Подставив это выражение в неоднородное уравнение, продифференцировав его по t и сократив на ei t, находим ,

Периодическую функцию cos t заменим в этом уравнении на функцию комплексного переменного ei t: поскольку вещественная часть ei t, а только вещественная величина имеет физический смысл, равна cos t.

Имеет место полная математическая аналогия в результатах рассмотрения электрических и механических колебательных систем. Если колебательная система обладает высокой добротностью Q и, соответственно, большим временем затухания по сравнению с периодом Т то процесс установления колебаний может затянуться и содержать в себе новые интересные физические явления.

Рассмотрим предельный случай, когда в системе можно пренебречь силами трения или сопротивлением = 0. Решение уравнения для вынужденных колебаний будет иметь в этом случае вид Предположим, что при t = 0 тело находится в состоянии покоя и имеет нулевую скорость: x(t) = 0,

В этом случае , с2 = 0 и можно переписать решение в виде Введем обозначения
6-1-1Kolebania_i_volny.ppt