elektr_5_8 Взаимодействие поля с веществом.ppt
- Количество слайдов: 46

Сегодня: Friday, February 16, 2018 Лекция Тема: ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ Содержание лекции: 1. Поглощение энергии неидеальным проводником 2. Импульс излучения 3. Отражение излучения от сверхпроводника 4. Взаимодействие излучения с диэлектриком 5. Показатель преломления 6. Электромагнитное излучение в ионизованной среде 7. Поле излучения точечных зарядов 8. Показатель преломления в конденсированных средах 9. Волны в металлах 10. Излучение Вавилова Черенкова

1. Поглощение энергии неидеальным проводником Рассмотрим взаимодействие электромагнитной волны с веществом в четырех различных случаях: плохой проводник, хороший проводник, диэлектрик и плазма. Плохой проводник частично поглощает энергию и импульс волны, и это позволяет оценить количество энергии и импульса, переносимого электромагнитной волной. Хороший проводник отражает электромагнитную волну со 100% ной эффективностью.

Через диэлектрик, такой как газ, волна распространяется, не испытывая поглощения, однако распространение волны в этом случае происходит медленнее, нежели в пустоте. В плазме существуют волны, распространяющиеся быстрее, чем в пустоте. Эти особенности находят свое объяснение при микроскопическом подходе, с учетом атомного строения вещества.

Движение заряда в веществе представляет еще одну интересную особенность электромагнитного взаимодействия в случае, если скорость движения заряда превышает фазовую скорость света в среде. При этом возникает новый вид электромагнитного излучения от равномерно движущегося заряда – излучение Вавилова Черенкова.
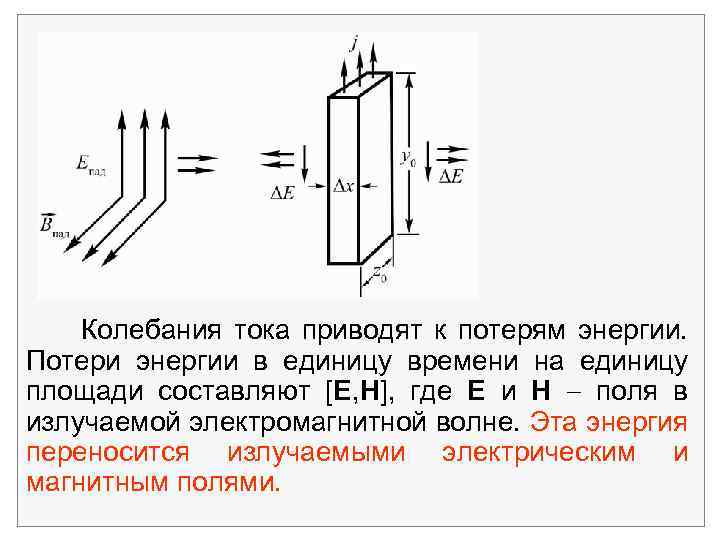
Колебания тока приводят к потерям энергии. Потери энергии в единицу времени на единицу площади составляют [E, H], где E и H поля в излучаемой электромагнитной волне. Эта энергия переносится излучаемыми электрическим и магнитным полями.

Если бегущая электромагнитная волна уносит от источника некоторую энергию, то, поставив на пути плоской волны поглощающую пластинку, можно уловить эту энергию. Пусть материал пластинки обладает конечной электропроводностью, это позволит определить полное количество джоулевой теплоты, выделившейся в пластинке. Согласно закону сохранения энергии, полное количество выделившейся теплоты соответствует энергии электромагнитной волны, поглощенной в пластине.

Поле само по себе обладает энергией. Плотность энергии электрического поля равна . Магнитная энергия, запасенная в единице объема, составляет. Если энергия заключена в электромагнитном поле, то джоулева теплота, выделившаяся в поглощающей пластинке, должно быть равным сумме этих двух величин.

Теряемая в единице объема внутри проводника мощность равна j. E. Если на проводящую пластинку падает монохроматическая плоская электромагнитная волна, то при этом выделяется теплота со скоростью j. E Вт/м 3, индуцированный ток j излучает электромагнитные волны. Пусть Е – поле, излучаемое индуцированным током j. На рисунке показано поле излучения для тонкой пластинки толщиной х. Обозначим поле падающей плоской волны через Епад. Эквивалентный поверхностный ток j х.

Если электропроводность достаточно низка, так что поле Е на расстоянии в одну длину волны внутри проводника почти не уменьшается, то отраженные волны компенсируют друга. Это объясняется тем, что для любой отраженной волны найдется волна, отраженная от более глубоких слоев, которая на обратном пути окажется сдвинутой по фазе на /2. (Горб одной из волн придется на впадину другой, и результирующая амплитуда окажется всюду равна нулю. )

В целом отраженные волны погасят друга при условии, что проводник не очень хороший. Это может быть графит или ионизованный газ. Если стопка пластинок бесконечно толстая, то поле Епад поглотится целиком. Поглощаемая единицей поверхности мощность определяется вектором Пойнтинга S. Направление потока энергии опреде ляется векторным произведением [Е, B] и совпадает с направлением вектора скорости распространения волны υ: S = wυ, где w – плотность энергии электромагнитного поля.

О взаимном гашении отраженных волн свидетельствует черный цвет графита (графит не отражает падающее на него электромагнитное излучение). То, что падающая волна поглощается, следует из непрозрачности достаточно толстого слоя графита.
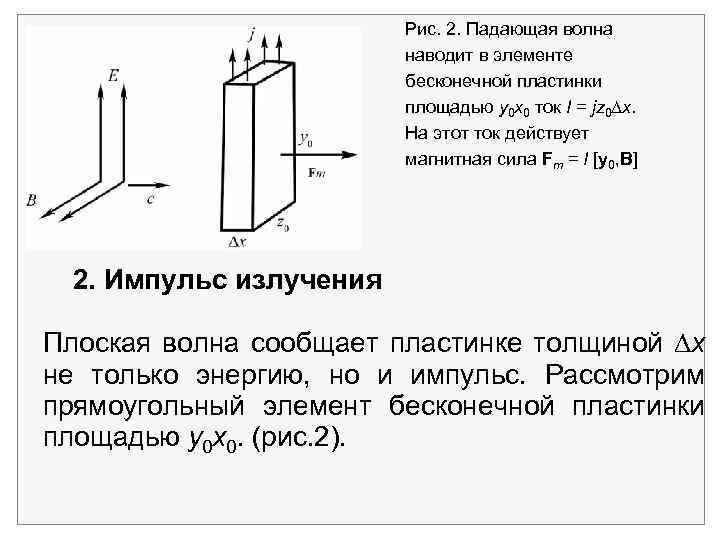
Рис. 2. Падающая волна наводит в элементе бесконечной пластинки площадью у0 х0 ток I = jz 0 х. На этот ток действует магнитная сила Fm = I [у0, B] 2. Импульс излучения Плоская волна сообщает пластинке толщиной х не только энергию, но и импульс. Рассмотрим прямоугольный элемент бесконечной пластинки площадью у0 х0. (рис. 2).

Импульс, сообщаемый элементу пластинки, dg = Fmdt или d. U = сdg, dg = d. U. Проинтегрировав по толщине пластинки х, находим g = U/c. d. U = с. Iy 0 Bdt –количество джоулева тепла от падающей волны. На элемент тока длиной у0, перпендикулярный падающему магнитному полю, действует сила Fm = I[у0, B] в направлении [Е, B], которое совпадает с направлением падающей волн

Поле излучения обладает не только энергией, но и импульсом. В любом эле менте объемаd. V поля излучения заключена энергия d. U = 0 E 2 d. V, а его импульс равен энергии, деленной на величину с. Иными словами, элемент объема d. V характеризуется вектором импульса (с учетом соотношения d. U = Sd. V/c) .

Поле излучения, которое испускается движущимся с ускорением зарядом, представляет само по себе физическую реальность. В каждой точке пространства оно имеет энергию и импульс, и их можно измерить. Энергию можно почувствовать, поместив руку в пучок света. Большая часть света поглотится рукой и превратится в теплоту. Из за малости величины 1/с измерить импульс светового пучка довольно трудно.

Предположим, что свет от лампы мощностью W = 100 Вт фокусируется на отражающей лопасти радиометра. Найдем силу давления на лопасть. Импульс пучка света дается выражением. Поскольку при отражении направление света меняется, передаваемый лопасти импульс оказывается в два раза больше по величине: .

. Таким образом, сила давления на лопасть Столь малая сила даже при ничтожном трении с трудом приводит лопасть в движение. Физическая сущность поля станет еще более реальной при изучении квантовой теории и свойств фотонов, поскольку излучение состоит из квантовых объектов – фотонов, которые столь же реальны, как электроны и протоны. Каждый фотон обладает энергией U = h и импульсом g = h /с, где – частота волны, a h – очень маленькое число, называемое постоянной Планка.

3. Отражение излучения от сверхпроводника В случае высокой проводимости электромагнитная волна поглощается не полностью, а частично отражается. Рассмотрим предельный случай = (сверхпроводник). Электрическое поле внутри сверхпроводника должно всегда обращаться в нуль (в противном случае неограниченно возрастал бы ток). Индуцированный поверхностный ток оказывается таким, что поле излучения Е = –Епад. При этом внутри пластинки результирующее поле отсутствует Е = Епад + Е = 0.

Слева от пластинки поле не обращается в нуль, поскольку его существование обусловлено двумя монохроматическими волнами одинаковой интенсивности, бегущими в противоположных направлениях. В этих условиях слева от пластинки (рис. 3) образуется стоячая волна с узлами и Величина индуцированного поверхностного тока Is(А/м), совпадает с током в источнике, генерирующем Епад. пучностями.
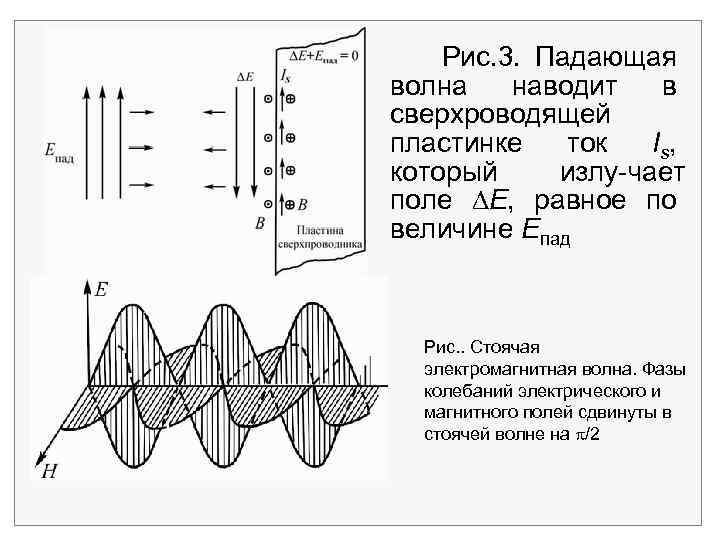
Рис. 3. Падающая волна наводит в сверхроводящей пластинке ток I s, который излу чает поле Е, равное по величине Eпад Рис. . Стоячая электромагнитная волна. Фазы колебаний электрического и магнитного полей сдвинуты в стоячей волне на /2

4. Взаимодействие излучения с диэлектриком Внешние электроны атомов диэлектрика связаны с атомом не жестко и под влиянием внешнего поля испытывают смещение. Вычислим величину такого смещения. Воспользуемся моделью атома, принятой в современной квантовой теории. Согласно этой модели, внешний электрон рассматривается в виде шарового облака радиусом R. Мы будем предполагать плотность заряда постоянной. При смещении распределенного шарового заряда на расстояние у от центра атома возникает возвращающая сила, пропорциональная y и направленная против смещения.

Вследствие этого электронное облако совершает гармонические колебания относительно центра атома у = y 0 cos 0 t. В центре атома находится ядро, окруженное облаком внутренних электронов, прочно связанных с ядром. Сила, действующая на внешнее электронное облако, согласно второму закону Ньютона равна

где 0/2 – частота собственных колебаний атомного электрона. Если на электронное облако действует поле Епад падающей волны, то результирующая сила запишется в виде Fрез = Fатом + (– e)Eпад, откуда получаем где е элементарный заряд.

Для обозначения смещения вместо х использована величина у, поскольку рассматривается случай, когда поле Епад направлено вдоль оси у. Падающую волну на расстоянии х от источника мы обычно описываем уравнением Епад = Е 0 cos (t – х/с). Поэтому Решением этого дифференциального уравнения служит гармоническая амплитудой волна с резонансной

Данное решение можно проверить прямой подстановкой в исходное уравнение. Таким образом, мы нашли, как взаимодействует отдельный атом с излучением. Рассмотрим множество таких атомов, из которых состоит твердая пластинка или слой газа.

5. Показатель преломления Пусть на пластинку толщиной х, состоящую из атомов, падает плоская волна. Электрическое поле падающей волны Епад вынудит атомные электроны совершать гармонические колебания. Любой колеблющийся электрон должен сам по себе излучать электромагнитную волну. Как и в случае пластинки из проводника, возникают отраженная и прошедшая волны, но потери на джоулеву теплоту в пластинке отсутствуют. Вся энергия сохраняется в форме электромагнитного излучения; таким образом, пластинка оказывается прозрачной.

Более того, если заимствовать известный из оптики результат, то окажется, что электромагнитная волна (или свет) распространяется внутри пластинки со скоростью u < с. Отношение с/u = n называется показателем преломления. У большинства твердых сред показатель преломления равен приблизительно 1, 5; это означает, что скорость света замедляется в них примерно на 33%. В таблице приведены показатели преломления используемых веществ. некоторых широко
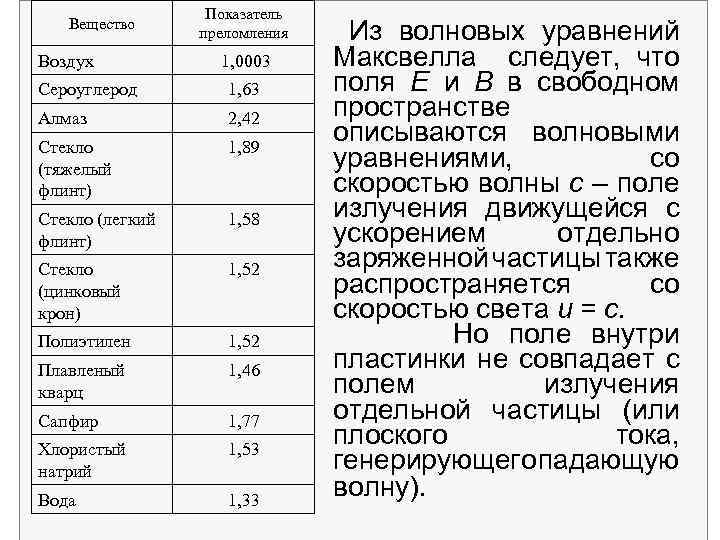
Вещество Воздух Показатель преломления 1, 0003 Сероуглерод 1, 63 Алмаз 2, 42 Стекло (тяжелый флинт) 1, 89 Стекло (легкий флинт) 1, 58 Стекло (цинковый крон) 1, 52 Полиэтилен 1, 52 Плавленый кварц 1, 46 Сапфир 1, 77 Хлористый натрий 1, 53 Вода 1, 33 Из волновых уравнений Максвелла следует, что поля Е и В в свободном пространстве описываются волновыми уравнениями, со скоростью волны с – поле излучения движущейся с ускорением отдельно заряженной частицы также распространяется со скоростью света u = с. Но поле внутри пластинки не совпадает с полем излучения отдельной частицы (или плоского тока, генерирующего падающую волну).

Поле внутри пластинки представляет собой суперпозицию поля падающей волны и полей излучения всех атомных электронов. Каждое из полей в отдельности распространяется со скоростью света u = с, но результирующее поле распространяется так, как если бы его скорость уменьшилась. Из решения следует, что поле излучения каждого из атомных электронов запаздывает по фазе на = 90 относительно поля падающей волны, которая приводит в движение эти электроны

В этом случае испущенная результирующая волна будет запаздывать по фазе относительно падающей. Ско рость результирующего волнового фронта меньше, чем u = с, хотя индивидуальные волны распространяются с u = с. Выведем формулу для показателя преломления в случае пластинки на рис. 4. Этот вывод можно выполнить следующим образом: 1. Задается электрическое поле падающей волны. 2. Вычисляется скорость, приобретаемая атомными электронами в пластинке под действием электрического поля падающей волны.
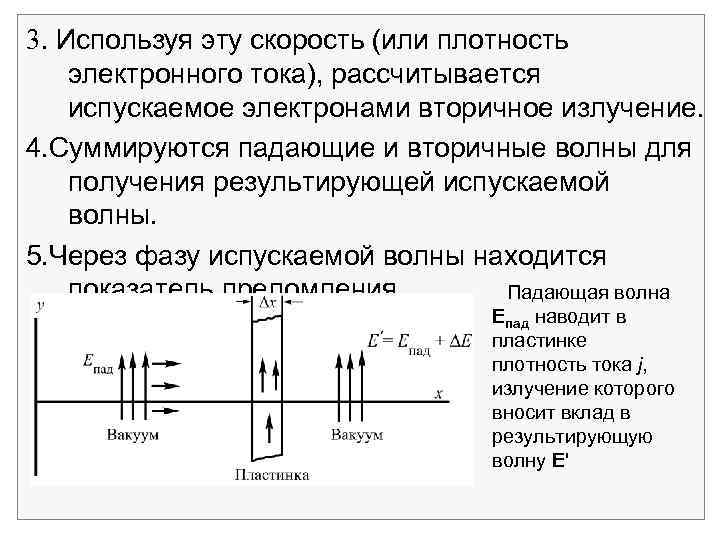
3. Используя эту скорость (или плотность электронного тока), рассчитывается испускаемое электронами вторичное излучение. 4. Суммируются падающие и вторичные волны для получения результирующей испускаемой волны. 5. Через фазу испускаемой волны находится показатель преломления. Падающая волна Епад наводит в пластинке плотность тока j, излучение которого вносит вклад в результирующую волну Е'

1. Падающая волна. Пусть электрическое поле падающей волны описывается гармоническим законом и распространяется со скоростью света: 2. Скорость электронов. Дифференцируя y(t) по времени, получаем выражение для скорости слабо связанных внешних электронов , где 0 – частота собственных колебаний электронов.

Плотность тока в пластинке j = N(–e)vy, где N – число колеблющихся атомных электронов в единице объема. Используя приведенное выше выражение для vy, находим

3. Излучение, испускаемое атомными электронами. Поле излучения у пластинки, создаваемое электронами пластинки, запишется в виде 3 нак «минус» указывает на то, что ток j и создаваемое им поле излучения имеют противоположные направления. Подставим сюда выражение для j:

и перепишем его в виде где

4. Результирующая волна. Результирующее электрическое поле испускаемой волны является суперпозицией поля падающей волны и поля, испускаемого атомными электронами: . Заменив Е найденным выражением, получим Здесь = (t – х/с). Хотя и увеличивается во времени, обе монохроматические волны сохраняют постоянную разность фаз, равную /2 радиан.

Эти две волны нетрудно сложить. В данный момент времени t первая волна представляет собой проекцию на ось х вектора Е 0 (рис. 5). Вторая волна является проекцией на ось х вектора Е 0, составляющего угол – /2 c первым вектором. Видно, что результирующий вектор Е'0 сдвинут по фазе относительно падающей волны на угол При выводе этого выражения мы воспользовались малостью углов (tg ), предположив, что Е 0/Е 0 << 1.
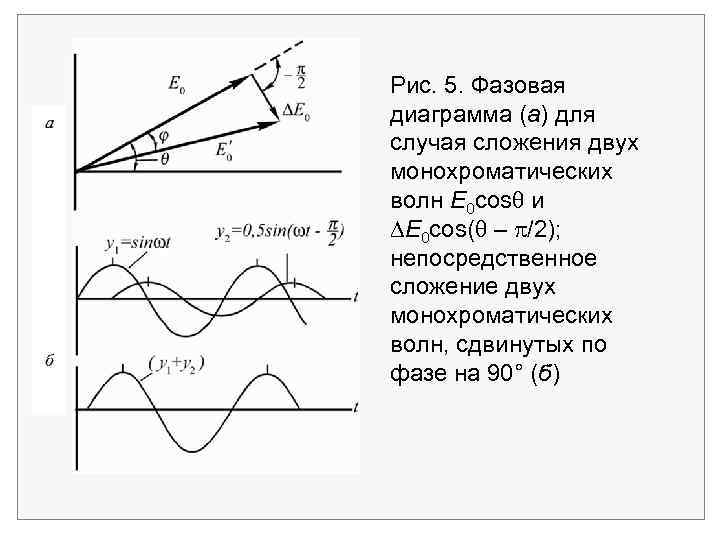
Рис. 5. Фазовая диаграмма (а) для случая сложения двух монохроматических волн E 0 cos и E 0 cos( – /2); непосредственное сложение двух монохроматических волн, сдвинутых по фазе на 90° (б)

5. Соотношение между фазовым сдвигом и показателем преломления. Падающая волна проходит через пластинку за время t = х/с, а волна, распространяющаяся со скоростью u = с/n, затрачивает большее время t' = n( х/с). Результирующий волновой фронт при прохождении пластинки задержится на t = (n – 1) х/с. Это соответствует фазовому сдвигу. . Поскольку = Е 0/Е 0, то.

Подставляя выражение для Е 0 и решая относительно n, находим показатель преломления Это показатель преломления пластинки. При выводе зависимости n( ) использовано условие, что поле падающей волны меняется слабо, т. е. (n – 1) << 1. Для больших n поле Eпад внутри пластинки следует заменить на результирующее поле

Дисперсия Полученный результат обеспечивает правильную зависимость показателя преломления от частоты падающего света (рис. 6). Для типичных атомов 0 > , причем относится к видимой области спектра. Этому соответствует показатель преломления больше единицы или скорость волны меньше с. Кроме того, при переходе частоты света из красной области спектра в фиолетовую показатель преломления увеличивается и возрастает отклонение светового луча призмой, т. е. имеет место нормальная дисперсия. Именно благодаря этому призма разлагает пучок белого света в спектр.
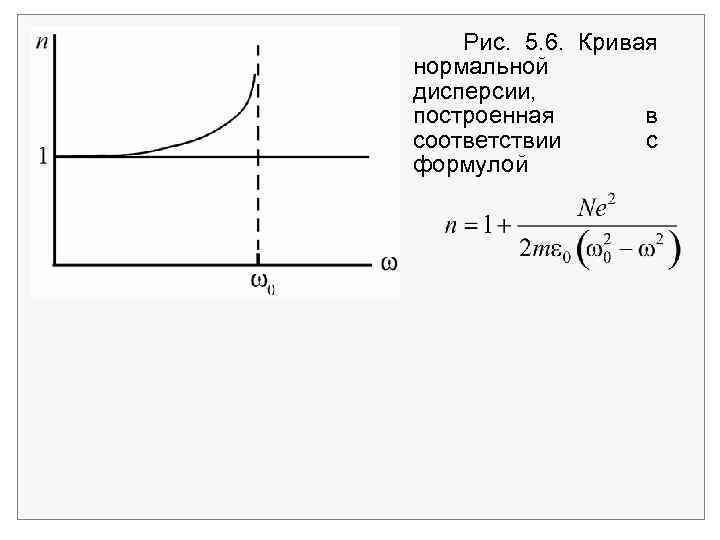
Рис. 5. 6. Кривая нормальной дисперсии, построенная в соответствии с формулой

Используя зависимость n = n( ) и данные таблицы, вычислим показатель преломления воздуха для ультрафиолетового излучения с = 3, 0 10– 7 м ( 0 = 7, 5 1015 с– 1). Для двух разных частиц имеем Из таблицы находим для воздуха n 1 = 1, 0003, причем 1 = 2 с/ = 3, 19 1015 с– 1 ( 1 = 5, 9 10– 7 м желтая линия натрия). Тогда где 2 = 3, 0 10– 7 м.

Таким образом, n = 1, 00082. Используя уравнения Максвелла и упрощенную атомную модель проводников и диэлектриков, удается рассчитать многие из наблюдаемых в природе общих свойств света и электромагнитного излучения.

Поле излучения, которое испускается движущимся с ускорением зарядом, представляет само по себе физическую реальность. В каждой точке пространства оно имеет энергию и импульс, и их можно измерить. Энергию можно почувствовать, поместив руку в пучок света. Большая часть света поглотится рукой и превратится в теплоту. Из за малости величины 1/с измерить импульс светового пучка довольно трудно.

Лекция окончена Нажмите клавишу <ESC> для выхода
elektr_5_8 Взаимодействие поля с веществом.ppt