c8060de97421fb9ce62771897f98ee95.ppt
- Количество слайдов: 38

Security Introduction Class 11 18 February 2003

Overview § Security Properties § Security Primitives § Sample Protocols

Introducing Protocol Participants § Alice (usually the protocol initiator) § Bob, Alice’s friend § Eve the eavesdropper § Mallory the malicious adversary § Trent the trusted server

Security Properties § Confidentiality (secrecy) • Eve cannot get any information • Semantic security – Even if Eve knows plaintext/ciphertext pairs, she cannot learn any new information § Integrity • Prevent modification § Authentication • Prevent impersonation • Bob knows that Alice sent message

Security Properties (cont) § Non-repudiation • Alice cannot deny having created message § Freshness • Bob knows that Alice’s message is recent • Replay protection – Mallory cannot replay Alice’s messages

Security Primitives § Asymmetric (public-private key) • Diffie-Hellman key agreement • Public-key encryption • Digital signature § Symmetric (shared-key, same-key) • Block cipher (pseudo-random permutation PRP) • Stream cipher (pseudo-random generators PRG) • Message authentication code (MAC) § Others (unkeyed symmetric) • One-way function • Cryptographic hash function

Asymmetric Primitives § Diffie-Hellman key agreement • • Public values: large prime p, generator g Alice has secret value a, Bob has secret b A B: ga (mod p) B A: gb Bob computes (ga)b = gab Alice computes (gb)a = gab Eve cannot compute gab

Asymmetric Primitives II § Problem: man-in-the-middle attack § Mallory can impersonate Alice to Bob, Bob to Alice • • • A M: ga (mod p) M A: gm M B: gm B M: gb Bob computes (gm)b = gbm Alice computes (gm)a = gam

Asymmetric Primitives III § Public-key encryption § El-Gamal encryption • • • Public values: large prime p, generator g Alice has public key ga (mod p), private key a Bob wants to send message M to Alice Bob picks random x, computes (ga)x = gax B A: gx, Mgax

Asymmetric Primitives IV § Digital Signatures § RSA signature • • • Alice has large secret primes p, q Pick e, compute d s. t. ed = 1 mod (pq) Public key N=pq, e Private key p, q, d Signature generation of message M = H(M)d mod N • Signature verification: e = H(M)ed = H(M)1 + K (pq) = H(M) (mod N)

Symmetric Primitives § Block cipher is a pseudo-random permutation (PRP), each key defines a one-to-one mapping § Encryption: EK(plaintext) = ciphertext § Decryption: DK(ciphertext) = plaintext § We write {plaintext}K for EK(plaintext) § Encrypt each block separately § Examples: DES, Rijndael

Symmetric Primitives II § Stream ciphers use pseudo-random generators (PRG) § PRG • Input: seed • Output: pseudo-random stream § Encryption: use shared key k and initialization vector IV for the seed ciphertext = plaintext PRG( k, IV ) § Send IV, ciphertext § Examples: RC 4, SEAL

Symmetric Primitives III § Message authentication codes (MAC) § “Cryptographic checksum”, keyed hash § Provides authentication, integrity § Send M, MAC( K, M ) § Example: HMAC-MD 5 • HMAC-MD 5(K, M ) = MD 5(K opad || • MD 5(K ipad || M)) ipad = 3636. . 36, opad = 5 C 5 C. . 5 C

Cryptographic Hash Functions § Maps arbitrary-length input into finite length output § Properties of a secure hash function • One-way: Given y = H(x), cannot find • • x’ s. t. H(x’) = y Weak collision resistance: Given x, cannot find x’ ≠ x s. t. H(x) = H(x’) Strong collision resistance: Cannot find x, x’ s. t. H(x) = H(x’) § Example: MD 5, SHA-1

One-Way Hash Chains § Versatile cryptographic primitive § Construction • Pick random r. N and public one-way function F • ri = F(ri+1) • Secret value: r. N , public value r 0 K 3 F K 4 F K 5 § Properties F K 6 F K 7 • Use in reverse order of construction: r 1 , r 2 … r. N • Infeasible to derive ri from rj (j<i) • Efficiently authenticate ri knowing rj (j<i): i-j • verify rj = F (ri) Robust to missing values

Comparison Sym vs Asym Crypto Symmetric crypto § 72 bit key for high security (2000) § ~1, 000 ops/s § 10 x speedup in HW Asymmetric crypto § 1024 bit key for high security (RSA) § ~100 signatures/s ~1000 verify/s (RSA) § Marginal speedup in HW

Sample Protocols § Sensor network encryption protocol (SNEP) § Broadcast authentication TESLA § Pay. Word § Micro. Mint

SPINS Assumptions § Communication • Frequent node-base station exchanges • Frequent network flooding from base • Node-node interactions infrequent § Base station • Sufficient memory, power • Shares secret key with each node § Node • Limited resources, limited trust

SNEP Security Goals § Secure point-to-point communication • Confidentiality • Secrecy • Authenticity • Integrity • Message freshness to prevent replay § Existing protocols use expensive asymmetric crypto (e. g. SSL/TLS, IPSEC)

Basic Crypto Primitives § Code size constraints code reuse § Uses block cipher encrypt function • Counter mode encryption • Cipher-block-chaining message authentication code (MAC) • Pseudo-random generator

SNEP Protocol Details § A and B share • Encryption keys: KAB KBA • MAC keys: K'AB K'BA • Counters: CA CB § To send data D, A sends to B: A B: {D}<K , C > , AB A MAC( K'AB , [CA || {D}<K , CA> ] AB )

SNEP Properties § Secrecy & confidentiality • Semantic security against chosen ciphertext attack • Strongest security notion for encryption § Authentication § Replay protection § Code size: 1. 5 Kbytes § Strong freshness protocol

Need to Stretch?
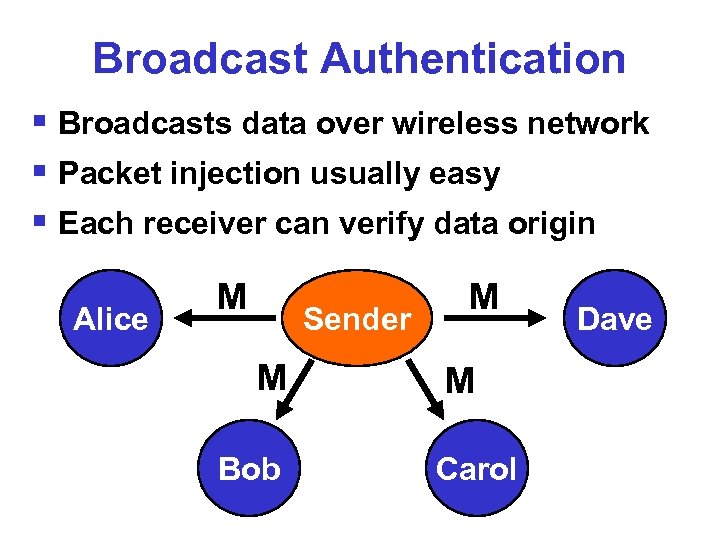
Broadcast Authentication § Broadcasts data over wireless network § Packet injection usually easy § Each receiver can verify data origin Alice M Sender M Bob M M Carol Dave
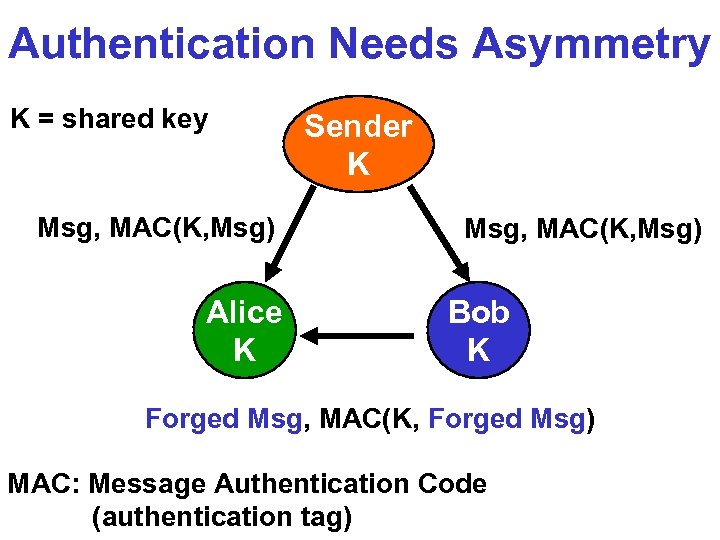
Authentication Needs Asymmetry K = shared key Msg, MAC(K, Msg) Alice K Sender K Msg, MAC(K, Msg) Bob K Forged Msg, MAC(K, Forged Msg) MAC: Message Authentication Code (authentication tag)

Digital Signatures Do Not Work § Signatures are expensive, e. g. , RSA 1024: • High generation cost (~10 milliseconds) • High verification cost (~1 millisecond) • High communication cost (128 bytes/packet) § Very expensive on low-end processors § If we aggregate signature over multiple packets, intolerant to packet loss

TESLA § Timed Efficient Stream Loss-tolerant Authentication § Uses only symmetric cryptography § Asymmetry via time • Delayed key disclosure • Requires loose time synchronization § Published in IEEE Security and Privacy 2000, NDSS 2001 [PCST]
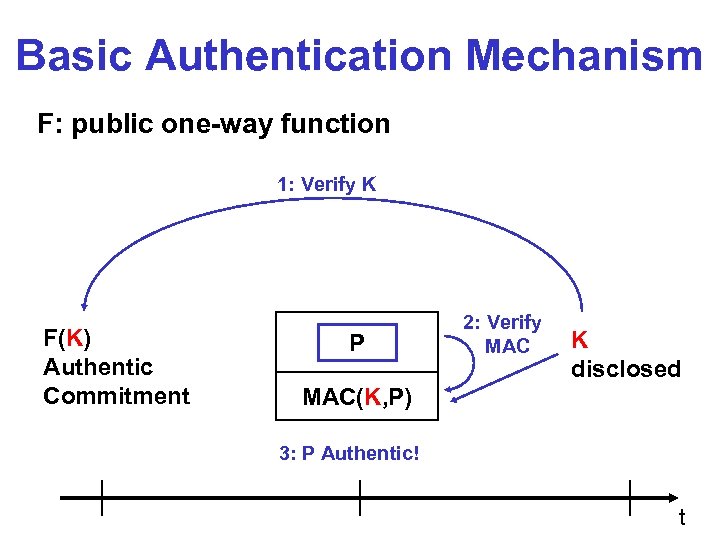
Basic Authentication Mechanism F: public one-way function 1: Verify K F(K) Authentic Commitment P 2: Verify MAC K disclosed MAC(K, P) 3: P Authentic! t

Security Condition § Receiver knows key disclosure schedule § Security condition (for packet P): on arrival of P, receiver is certain that sender did not yet disclose K § If security condition not satisfied, drop packet
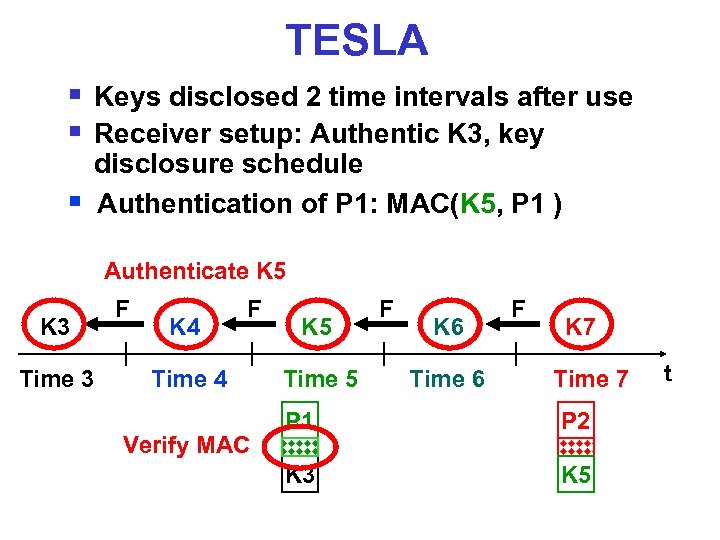
TESLA § Keys disclosed 2 time intervals after use § Receiver setup: Authentic K 3, key § disclosure schedule Authentication of P 1: MAC(K 5, P 1 ) Authenticate K 5 K 3 Time 3 F K 4 F Time 4 Verify MAC K 5 Time 5 F K 6 Time 6 F K 7 Time 7 P 1 P 2 K 3 K 5 t
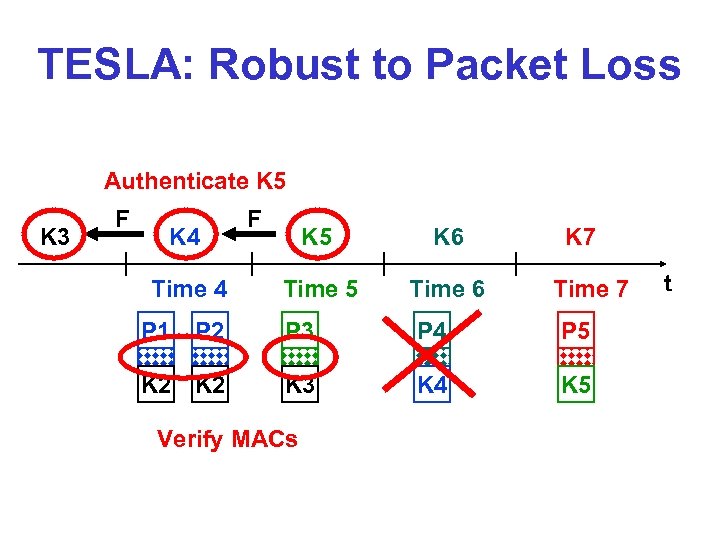
TESLA: Robust to Packet Loss Authenticate K 5 K 3 F K 4 Time 4 P 1 F K 5 K 6 Time 5 Time 6 K 7 Time 7 P 2 P 3 P 4 P 5 K 2 K 3 K 4 K 5 Verify MACs t

TESLA Summary § Low overhead § § • Communication (~ 20 bytes) • Computation (~ 1 MAC computation per packet) Perfect robustness to packet loss Independent of number of receivers Delayed authentication Extensions: • TIK: Instant key disclosure • Heterogeneous receivers • Instant authentication (sender buffers data)
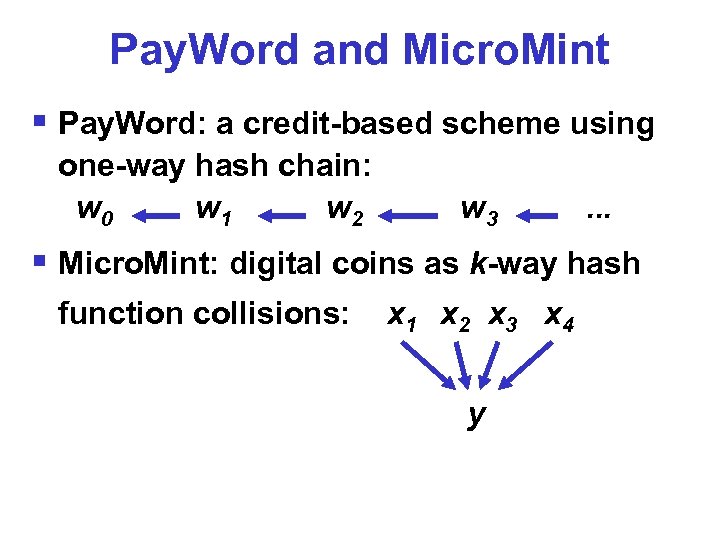
Pay. Word and Micro. Mint § Pay. Word: a credit-based scheme using one-way hash chain: w 0 w 1 w 2 w 3 . . . § Micro. Mint: digital coins as k-way hash function collisions: x 1 x 2 x 3 x 4 y
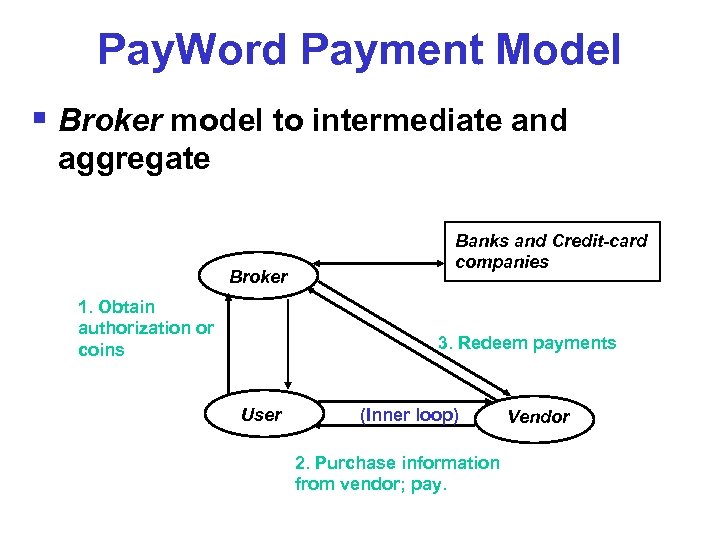
Pay. Word Payment Model § Broker model to intermediate and aggregate Broker 1. Obtain authorization or coins Banks and Credit-card companies 3. Redeem payments User (Inner loop) 2. Purchase information from vendor; pay. Vendor

Pay. Word § Broker signs User’s public key (certificate) § User creates one-way hash chain to buy goods from vendor, c 0 , …, c. N § Each one-way chain element has value v § User signs c 0 and sends it to vendor § User can incrementally pay by revealing successive elements ci § Vendor redeems payment by cashing largest element cj , value = v*j

Micro. Mint § A digital coin should be: • Hard to produce [except by Broker] • Easy to verify [by anyone] § Digital signatures “work, ” but are relatively expensive § Micro. Mint uses hash functions only (no public-key crypto) § Broker utilizes economy of scale to produce Micro. Mint coins cheaply (as with a regular mint)
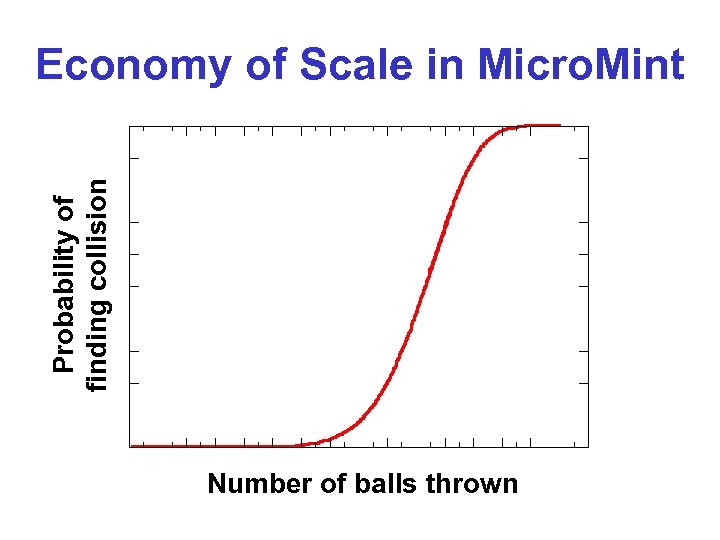
Probability of finding collision Economy of Scale in Micro. Mint Number of balls thrown

Minting Micro. Mint Coins § Pick a one-way hash function F, mapping § § § inputs to n-bit outputs A valid coin is a k-way collision Find v 1, …, vk, s. t. F(v 1) = … = F(vk) Verification is very efficient Producing first 2 -way collision requires time 2 n/2 (birthday paradox) Producing first k-way collision requires time Nk = 2 n(k-1)/k Time c. Nk yields ck coins; once threshold of Nk is passed, coins are produced rapidly
c8060de97421fb9ce62771897f98ee95.ppt