Security in Outsourced Association Rule Mining Agenda

Security in Outsourced Association Rule Mining

Agenda Introduction ¡ Approximate randomized technique ¡ Encryption ¡ Summary and future work ¡

Introduction ¡ Data mining in company l l ¡ know about the past activities of their customers make strategic decisions Types of data mining l l l Association rules mining Clustering Classification

Association rules ¡ “X => Y” l l l If a transaction contains itemset X, the transaction will probably contain itemset Y Support: number of supporting transactions Confidence: proportion of transactions containing X which also contains Y

Performing data mining ¡ Build application l l ¡ Buy software l l ¡ Development cost? Time? Fit requirements? Maintenance? Outsource

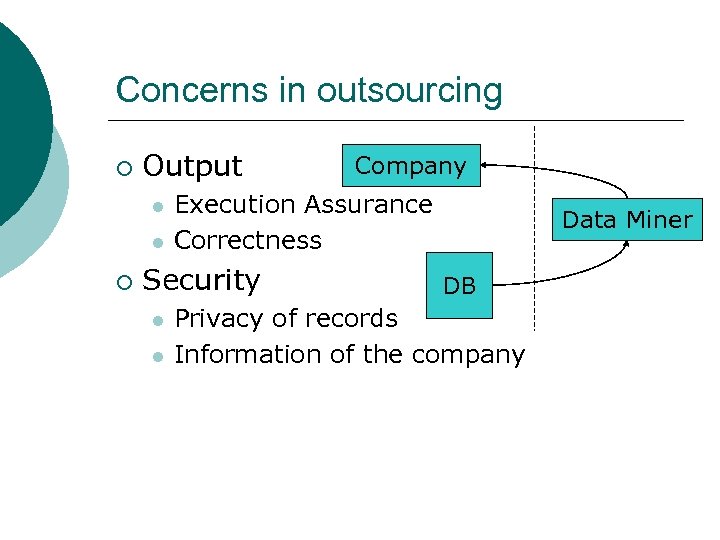Concerns in outsourcing ¡ Output l l ¡ Execution Assurance Correctness Security l l Company Data Miner DB Privacy of records Information of the company

Approximate randomized technique

Approximate solution ¡ Privacy Preserving Mining of Association Rules l l SIGKDD 2002 Authors: Alexandre Evfimievski, Ramakrishnan Srikant, Rakesh Agrawal, Johannes Gehrke

Problem formulation Let the set of transactions be T = {t 1, t 2, … t. N} ¡ Transform T to T’ = {t’ 1, t’ 2, … t’N} ¡ Mine in T’ ¡ Privacy breaches ¡ l Itemset A cause a privacy breach of level p if for some item a in A ¡ P[a in ti|A in t’i] >= p

Select-a-size randomization ¡ For each transaction ti in T l l m = length of ti Select (non-uniformly) randomly an integer j from [0, m] Copy uniformly at random j items in ti to t’i Consider every item a not in ti, add a to t’i with a given probability pm

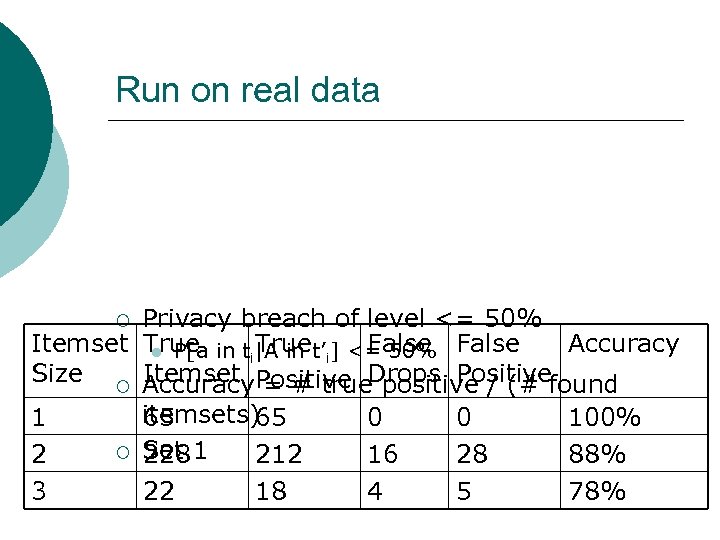Run on real data Privacy breach of level <= 50% Itemset True in ti|A in t’i] <= 50% False True False Accuracy l P[a Size ¡ Accuracy Positive Drops Positivefound Itemset = # true positive / (# itemsets)65 1 65 0 0 100% ¡ Set 1 2 228 212 16 28 88% 3 22 18 4 5 78% ¡

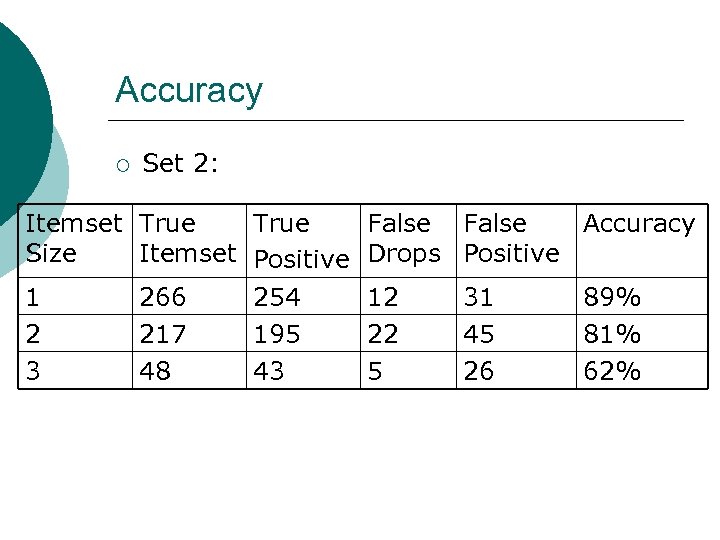Accuracy ¡ Set 2: Itemset True Size Itemset Positive 1 266 254 2 217 195 3 48 43 False Accuracy Drops Positive 12 22 5 31 45 26 89% 81% 62%

Problems ¡ Estimated counts of large itemsets varies l ¡ "beer and diaper" story l l ¡ Lower accuracy of association rules customers who buy diapers tend also to buy beer hard to believe some strange rules Expensive to make wrong decision l l Supermarket: layout design Health center: identify new disease

Security concerns Individual transaction is protected ¡ Private association rules can be estimated by other parties ¡ l Adversary actions may be based on found association rules

Encryption

Problem formulation Let the set of transactions be T = {t 1, t 2, … t. N} ¡ I is the entire set of items ¡ l All ti is a subset of I Transform T to T’ = {t’ 1, t’ 2, … t’N} ¡ A third party mines in T’ and gets AR’ ¡ Transform AR’ to AR ¡

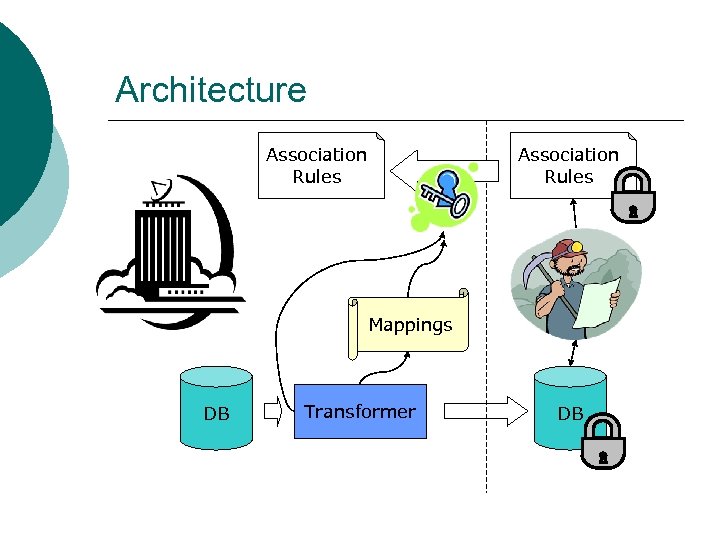Architecture Association Rules Mappings DB Transformer DB

Encryption ¡ To protect a message, simple encryption can be applied l ¡ Association rule encryption l l ¡ “GOOD DOG” can be encrypted as “PLLX XLP” 752 => 891? Milk => Bread Transaction encryption l l <8, 69, 153, 756>?

Simple scheme Encryption ¡ For every transaction ti ¡ l For every item x in ti ¡ ¡ Add f(x) to t’i where f is a bi-jective function Decryption l For every association rule ri ¡ For every item y in r l Replace y by f-1(y)

Problems with simple encryption ¡ They are easy to crack l “PLLX XLP” ¡ l 26 P 3 combinations, with at least one vowel Association rules ¡ # Bread > # Car # association rules, # large itemsets are disclosed ¡ Solution ¡ l Use a more complex scheme

Fake items ¡ Probability to make a correct guess of a single mapping l ¡ = 1 / |I| Randomly add some fake items to each transaction l Decrease the above probability to 1 / (|I| + |F|)

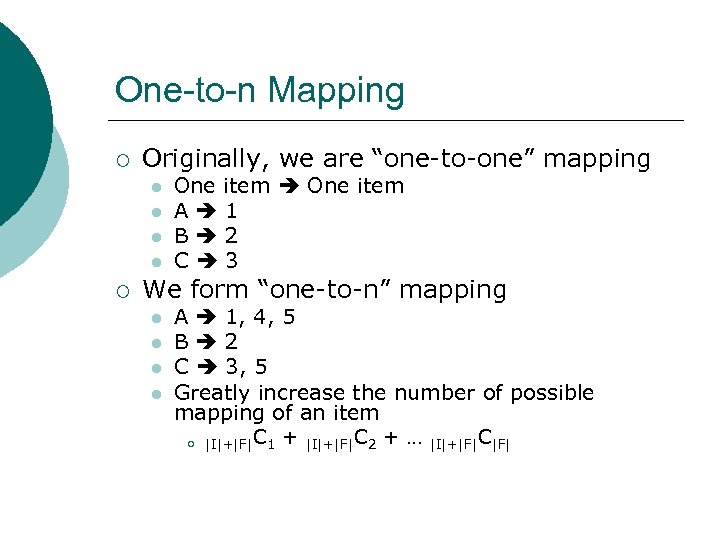One-to-n Mapping ¡ Originally, we are “one-to-one” mapping l l ¡ One item A 1 B 2 C 3 We form “one-to-n” mapping l l A 1, 4, 5 B 2 C 3, 5 Greatly increase the number of possible mapping of an item ¡ |I|+|F|C 1 + |I|+|F|C 2 + … |I|+|F|C|F|

Example transformation ¡ T= l l l l {A} {B} {C} {A, B} {A, C} {B, C} {A, B, C} ¡ T’ = l l A 1, 4, 5 B 2 C 3, 5 l l l {1, 4, 5} {2} {3, 5} {1, 2, 4, 5} {1, 3, 5} {2, 3, 5} {1, 2, 3, 4, 5}

Limitation on the mapping f ¡ For any item x, there does not exist items y 1, y 2, …, yk (x ≠ y 1 ≠ … ≠ yk ) l ¡ Such that f(x) subset in f(y 1) U f(y 2) U…f(yk) Consider an example l l l A 1, 2 B 2, 3 C 3, 4 AC 1, 2, 3, 4 ABC 1, 2, 3, 4

Limitation on the mapping f ¡ For any item x l ¡ f(x) – Ui != x, i in I f(i) != empty Every item must map to something unique

Mapping generation – Item Extend Initialize every item to map to something unique I’ ¡ For every item x in IE ¡ l l Randomly pick some mappings Extend each mapping by x

Example run A 1 ¡ B 2 ¡ C 3 ¡ IE = {4, 5} ¡

Considering item 4 ¡ ¡ ¡ A 1 B 2 C 3 ¡ ¡ ¡ Pick A A 1, 4 B 2 C 3

Considering item 5 ¡ ¡ ¡ A 1 B 2 C 3 ¡ ¡ ¡ Pick A, C A 1, 4, 5 B 2 C 3, 5

Item Extend ¡ Every item must map to something unique A 1, 4, 5 l Say 1 is unique to f(A) B 2 C 3, 5 supp. T(A) = supp. T’(1) ¡ For a transaction t without item A ¡ l l Add a subset of unique mapping set to t’ with some probability {1, 4} is unique mapping set in f(A) ¡ {}, {1}, {4}, {1, 4} may be added

Fake items again Now, every item in t’i must be in some mappings ¡ Randomly add some fake items in |F| to each transaction ¡ Mapping f: I -> |I’| U |IE| U |F| ¡ l l l |I’|: core “unique” items |IE|: expanding items |F|: fake items

Basic transformation framework ¡ For each transaction t l For each item x in t ¡ l For item i in I - t ¡ l Add f(x) to t’ Add randomly subset of unique mapping set of f(i) to t’ For item f in F ¡ Toss a biased coin for each item, add f to t’ if head (probability should be difference)

Recovering association rules ¡ Given an encrypted rule in AR’ l ¡ If there exists i 1, i 2, …, im in I l ¡ r’: X => Y Uk=1 m f(ik) = X And there exists j 1, j 2, …, jn in I l Uk=1 n f(jk) = XUY r: {i 1, i 2, … im} => {j 1, j 2, …, jn} – {i 1, i 2, … im} is a rule in AR ¡ Otherwise, the rule is not correct ¡

Example ¡ Given l l l 1 => 4 (rejected) 2 => 1, 5 (rejected) 2 => 1, 3, 4, 5 (B => AC) 2, 3, 5 => 1, 4 (BC => A) 2, 3, 5 => BC ¡ 1, 2, 3, 4, 5 => ABC ¡ Mapping f A 1, 4, 5 B 2 C 3, 5

Correctness ¡ Proposition l For any item x, y, f is transformation mapping supp. T(x) = supp. T’(f(x)) ¡ supp. T(x. Uy) = supp. T’(f(x) U f(y)) ¡ l For any itemset X, Y, F is the transformation mapping supp. T(X) = supp. T’(F(X)) ¡ supp. T(XUY) = supp. T’(F(X) U F(Y)) ¡ ¡ No false drops and false positives

Summary ¡ Generation of mappings l l ¡ Transformation of transactions l l l ¡ One-to-n mappings Item Extend Mapping f(x) Subsets of unique mapping set Fake items Recovering association rules l Reverse mappings and filtering

Test run # Items = 1 k, |T| = 1 k ¡ Without transformation ¡ l l ¡ One rule Time: 8 s Item Extend l l l 147 rules Total times: 26 s Mappings generation and transformation: 219 ms

Future Work ¡ Define parameters to the problem l l Size of |IE| Size of |F| Give a clear measure of security ¡ Give a clear measure of overhead ¡ Correctness of association rules ¡ l l Query execution proof Result verification

The End

Choosing probability Uniform distribution or any fixed distribution give patterns which may be easily identified ¡ Random probability distribution ¡ l l {}: 70%, {1}: 5%, {4}: 15%, {1, 4}: 20% Storage: need additional storage Back

Algorithm for transformation Transformation is the most costly process ¡ Execution time linear to database size |T| ¡ Should be as fast as possible ¡

Optimization ¡ Mapping Retrieval l ¡ For an item x, use a hash table to retrieve the mapping, h(x) Adding fake items l l l First randomly (according to the probability of adding items) determine the number of items to add Randomly pick in the set (non-uniform distribution) Gives a much shorter runtime in average

Choice of mapped items ¡ ¡ Acceptable as long as it is not easy to identify I’, IE, F One way is to use random permutation of first |I| + |IE| + |F| natural numbers 1 2 … |I|+|IE|+|F| * (1+ δ) ¡ ¡ First |I| numbers are mapped to |I’| Next |IE| numbers are IE

Cut and paste randomization ¡ ¡ One case of select-a-size randomization The way to perform selection of j l l l ¡ Given an integer Km > 0 Randomly choose j in [0, Km] If (j > m) ¡ Set j = m Overall input parameters l l Km pm

Effects on support ¡ Support of A in T’ l l ¡ A in t, without replaced A’ in t, randomly add A Support of AB in T’ l l AB in t, without replaced A and B AB’ in t, randomly add B A’B in t, randomly add A A’B’ in t, randomly add A and B

Estimating original support ¡ Support of A in T, x l l ¡ Support of A in T’, y x * P(A remains in original transaction) + (|DB| - x) * pm = y Support of AB in T l l l Support of AB in T’ Support of AB’, A’B in T’ Support of A’B’ in T’

Apriori property Suppose m = 2 for all t in T ¡ |T| = 10, |I| = {A, B} ¡ pm= 0, j = 1, ¡ Support of B in T’ supp. T’ (B)= 0 ¡ l E(supp. T(B)) = 0 supp. T’ (A)= 10 ¡ supp. T’ (AB)= 0 ¡ E(supp. T(AB)) = supp. T’ (A) * 1 = 10 ¡

Apriori property An expected large itemset may have an expected small sub-set ¡ But generally the support of subsets are not too small ¡ Instead of using the support threshold to filter all small candidates, use a smaller value ¡

Apriori algorithm Generate candidate sets ¡ Scan database for counts ¡ Recover the predicted support ¡ Discard candidates with support smaller than <= candidate limit ¡ Save for output candidates with support >= support threshold ¡ Apriori_gen(remaining candidate) ¡

Candidate limit ¡ A high value l l ¡ A small value l l ¡ Increase numbers of false drops Poor correctness Increase number of candidate sets High running time Experiment l l l Support threshold: smin estimated s. d. : δ smin – δ is found to be a good value

Other applications Outsourced transaction database (secure) storage ¡ Outsourced association rule mining using data stream ¡ Secure distributed association rule mining with third party miner ¡

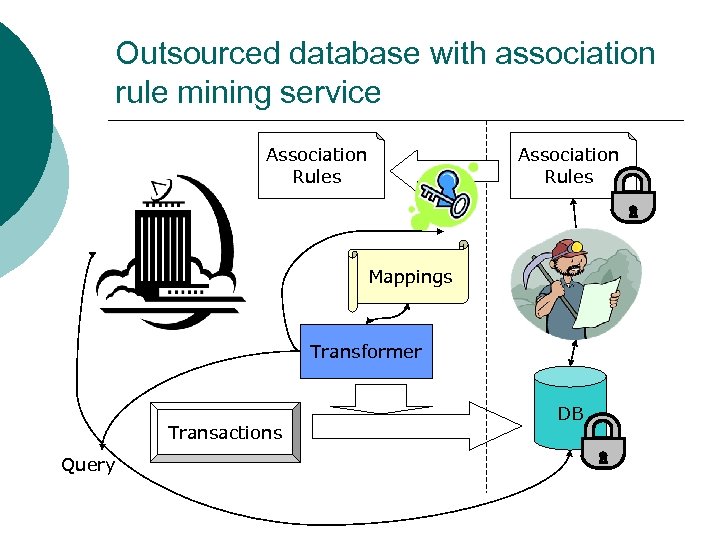Outsourced database with association rule mining service Association Rules Mappings Transformer Transactions Query DB